热套式超高压容器的设计及有限元分析

翟培培

（西安石油大学机械工程学院）

压力容器

热套式超高压容器的设计及有限元分析

翟培培*

（西安石油大学机械工程学院）

设计了工作压力为600 MPa、容量为200 L的超高压容器筒体，并利用有限元软件ANSYS对其进行分析，得到了筒体在预应力和实际工作两种状态下的应力分布结果。经优化取得了内外筒体的最佳过盈量及界面半径，使得各层筒体的应力分布基本均匀。

超高压容器 应力分布 有限元分析 热套式 筒体 预应力

双层热套式筒体作为超高压容器的关键部件，在设计时对其结构、强度以及材料等都提出了苛刻的要求。本文将双层热套式高压容器筒体的受力过程分为预应力状态以及合成（工作)状态[1]。在实际情况中，内外筒体是作为整体运行的，内外筒体接触（配合）具有微小的过盈量，这种情况属于经典的接触非线性分析问题[2]。这种问题在分析时须考虑过盈状态下的各向应力和应变分布情况，以及内筒加载内压时筒体的应力变化情况，这样才能真正地模拟仿真工作状态下筒体的受力状况[3]。

1 筒体的设计

超高压容器筒体的主要形式是厚壁圆筒，其应力沿整个壁厚方向的分布十分不均匀，而且径比越大，不均匀性越显著[4]。目前，超高压容器的结构形式主要有单层厚壁式、多层热套式和缠绕式等多种[5]。经过全面考虑各种结构形式各自的特点以及我国的超高压容器制造能力，本文所设计的超高压容器采用双层热套式。

该超高压承压筒体的最大工作压力为600 MPa，按设计要求确定内径Di为300 mm，经计算取筒体有效长度L为3 800 mm，外径Do为960 mm，壁厚t为330 mm，内筒的外径和外筒的内径之间形成Δ为0.50mm的过盈量。双层热套式筒体的结构如图1所示。选择0Cr17Ni4Cu4Nb作为内、外筒的材料，其机械性能如表1所示[6]。

图1 双层筒体结构

表1 0Cr17Ni4Cu4Nb材料机械性能

2 筒体的有限元分析

2.1 几何模型的导入

本文分析的筒体模型较简单，且是轴对称的，属于平面应变问题[7]。为了方便计算，在Solidworks中建立二维模型，选取1/4筒体模型导入ANSYS Workbench中作为计算模型，模型采用的几何尺寸见图1。本文中缩套内外筒径的过盈量Δ为0.50 mm，分别对筒体在预应力和实际工作两种状态下进行模拟计算，分析其两种状态下应力的分布情况。导入的模型如图2所示。

图2 筒体模型

2.2 定义材料属性

输入材料属性：弹性模量E=2.13×105MPa，泊松比λ=0.27，材料屈服极限σs=1 180 MPa，材料密度 ρ=7.78×103kg·m-3。

2.3 网格划分

由于本文所选择的模型几何形状较规则且简单，所以将其设置为四边形网格划分形式，网格划分模型如图3所示。

图3 网格划分模型

2.4 设置接触

内筒外壁和外筒内壁之间形成了面与面的接触对，这时在ANSYS Workbench里将外筒内壁设置为目标面，将内筒外壁设置为接触面，将其接触类型改为摩擦接触。设置目标单元为Target 169，接触单元为Contact 172，接触为增广拉格朗日函数，初始过盈量为0.5 mm。

2.5 施加边界条件

将Frictionless Support分别施给内外筒的X轴和Y轴，也就是使模型最上侧垂直方向全部的节点沿X轴方向上自由度为零；使模型最下方水平方向上全部节点在Y轴方向上的自由度为零[8]，图4为加载的边界条件。图5为预应力下内外筒接触部位的界面压力。

图4 加载的边界条件

图5 预应力下内外筒接触部位的界面压力

2.6 求解

第一步计算静态过盈配合时内外筒体的各向应力状态；第二步在预应力的基础上加载600 MPa的压力于内筒内壁，此即为筒体的实际工作状态。

3 结果分析

表2～表4是预应力状态下理论计算所得的筒体各向应力数值，与ANSYS有限元仿真的结果进行比较，从表中可以看出不管是周向应力、径向应力还是等效应力，ANSYS有限元分析的数值和理论计算值基本相近，且最大相对误差值小于5%。表5～表7为工作状态下计算所得的筒体周向应力、径向应力和等效应力值与有限元仿真的结果进行的比较，同样可以得到以上的结论。这说明两种状态下各向应力的理论计算值与有限元仿真结果均基本吻合，验证了其分析的准确性。

表2 预应力下筒体不同位置周向应力值对照

表3 预应力下内外筒体不同位置径向应力值对照

表4 预应力下内外筒体不同位置等效应力值对照

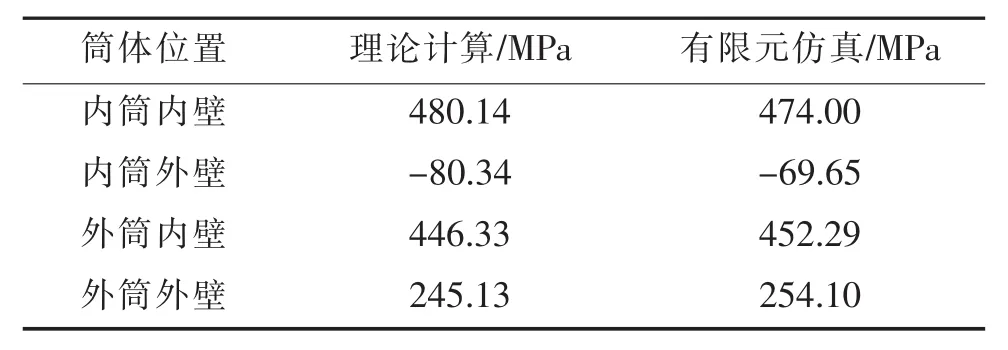
表5 工作状态下内外筒体不同位置周向应力值对照

表6 工作状态下内外筒体不同位置径向应力值对照

表7 工作状态下内外筒体不同位置等效应力值对照

从图6可直观看到预应力下内外筒体等效应力的分布情形，外筒内壁为最大应力位置处，其值为277 MPa，由内筒的内壁到内筒外壁等效应力呈现逐渐降低的变化，等效应力在内外筒壁接触处发生了突变，由外筒的内壁到外筒外壁等效应力又逐渐降低。

图6 预应力下的应力分析结果

图7为工作状况下的筒体的应力变化情形，从图中看出当给内筒施加600 MPa的内压时，应力由内筒向外筒渐渐地发生了转移，内外筒体的内壁一直是应力危险部位，这模拟了筒体的实际受力情况。

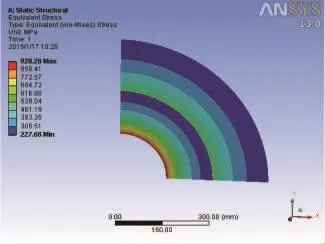
图7 工作状态下的应力分析结果

4 关键尺寸优化

从上面超高压容器筒体有限元分析和理论计算结果可以看出，工作状态下筒体的最大等效应力没有达到材料的屈服极限，说明它还是处于材料的弹性变形阶段。从内筒内壁到外筒内壁等效应力的变化率来看，筒体的应力分布极其不均匀；且原容器内外筒体径比没有达到双层筒体的最优设计条件。基于上面两点，我们对其进行了结构优化，以获得更为合理的筒体结构。在本文中我们主要针对超高压筒体的中径以及过盈量进行优化设计分析。

从弹性失效理论知道，剪切应力引起压力容器的失效。双层热套式筒体在工作状态下，最大应力出现于内、外筒体的内壁。因此，最优化设计就是要满足内、外筒体的内壁剪切应力相等[9]。

4.1 优化设计

（1）设计变量。筒体中径变量初始值R12为300 mm，过盈量Δ为0.5 mm。

（2）输出变量。输出变量为筒体的最大等效应力，在此主要提取的是内外筒体内壁的等效应力，因为内外筒体内壁是应力集中的位置，在这两个位置如果不发生失效，筒体就是安全的[10]。

4.2 优化的结果

经过多组数据的优化，选出9组优化点（如表8所示），从结果看出第6组为最优解。经优化后，内外筒的剪切应力及等效应力已经很接近，其应力的变化率从内筒内壁到外筒内壁明显减小，与之前初选的界面半径及过盈量相比，筒体的应力分布更均匀了，应力状况有了相当的改善。

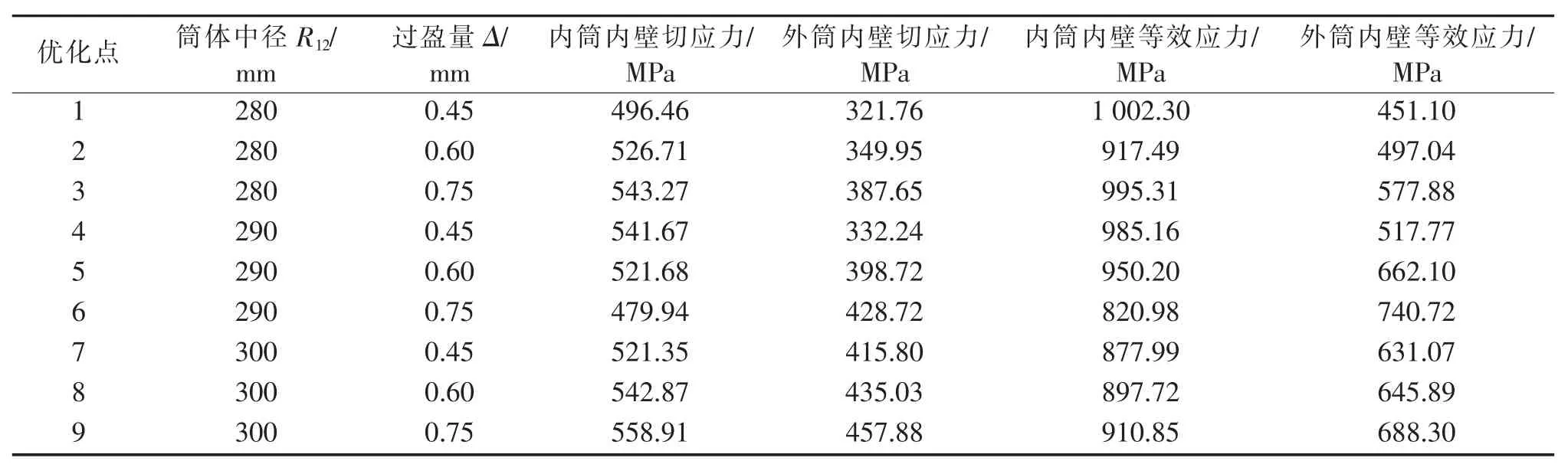
表8 优化结果

5 结论

本文设计了工作压力为600MPa、容量为200L的超高压容器的筒体，并利用有限元软件ANSYS对其进行了分析，模拟了筒体实际的工作过程，得到了筒体在预应力状态和工作状态下的应力分布情况。从分析结果可以看出，在整个工作过程中，最大等效应力出现在工作状态下内筒的内壁，其值为820 MPa，未达到筒体材料0Cr17Ni4Cu4Nb的屈服极限（1 180 MPa），满足设计要求。此外，经优化设计取得了最佳内外筒体的过盈量和中径。这对热套式超高压容器的设计有一定的参考意义。

[1]张于贤，王红．关于材料屈服强度的实验研究 [J]．材料工程，2005（11）：43-45．

[2]张朝晖．ANSYS 11.0结构分析工程应用实例解析 [M]．北京：机械工业出版社，2008：234-236．

[3]何景晖，张悦．450 MPa超高压缸筒的有限元分析 [J]．锻压装备与制造技术，2008，43（6）：50-52.

[4]帅长红.液压机设计、制造新工艺新技术及质量检验标准规范实务全书[M].北方工业出版社，2006.

[5]邵国华，魏兆灿．超高压容器[M]．北京：化学工业出版社，2002：17-37．

[6]陈浩，陈小敏，马慧珍，等．热套式超高压容器筒体有限元分析及优化 [J]．当代化工，2015， 44（2）： 417-420．

[7]曾攀．工程有限元方法[M]．北京：科学出版社，2010．

[8]徐长江,李东升，窦建鹏，等.缩套式超高压容器筒体的有限元分析[J].锻压装备与制造技术，2011（6）：83-86.

[9]张于贤，王红．缩套超高压缸的最佳化设计 [J]．机械设计与研究，2006，22（5）：115-117．

[10]王凤生，吴大华，包河山．压力容器设计方法探讨 [J]．一重技术，2004（1）：5-7．

Design and Finite Element Analysis of Heat Sleeve Ultra-high Pressure Vessel

Zhai Peipei

The cylinder of an ultrahigh pressure vessel with a pressure of 600 MPa and a capacity of 200 L was designed.The finite element software ANSYS was used to analyze the stress distribution in the two states of prestress and actual work.The optimum interference and interface radius of the inner and outer cylinder were obtained by optimization,and the stress distribution in each layer of the cylinder was basically uniform.

Ultra-high pressure vessel;Stress distribution;Finite element analysis;Heat sleeve type;Cylinder;Prestress

TQ 052.4

10.16759/j.cnki.issn.1007-7251.2017.10.011

*翟培培，女，1989年生，硕士研究生。西安市，710065。

2017-05-01）