基于经验模式分解的滚动轴承故障诊断方法
宁继荣,刘 尧
(1.西北工业大学航天学院,陕西 西安 710065;2.西安航天远征流体控制股份有限公司,陕西 西安 710100)
基于经验模式分解的滚动轴承故障诊断方法
宁继荣1,刘 尧2
(1.西北工业大学航天学院,陕西西安710065;2.西安航天远征流体控制股份有限公司,陕西西安710100)
针对滚动轴承故障诊断中,冲击脉冲法(Shock Pulse Method, SPM)结合包络解调技术进行定量诊断误差较大的问题,提出了基于经验模式分解(Empirical Mode Decomposition, EMD)和SPM的滚动轴承故障定量诊断方法。该方法首先对轴承振动信号进行EMD分解,再对分解得到的基本模式分量 (Intrinsic Mode Functions, IMFs)做包络解调从而得到准确的冲击值,然后利用SPM方法便可以准确地进行滚动轴承故障定量诊断。试验验证结果表明,内圈故障特征频率处出现22.12 dB的峰值,根据SPM方法判断该轴承存在轻微内圈故障,符合实际情况,该方法可以准确有效地进行滚动轴承故障定量诊断。
经验模式分解;滚动轴承;故障诊断
0 引言
滚动轴承是旋转机械中应用最为广泛的机械零件,也是最易损坏的元件之一。滚动轴承在运转过程中可能会由于各种原因引起损坏,如装配不当、润滑不良、水分和异物侵入、俯蚀和过载等都可能会导致滚动轴承过早损坏。即使在安装、润滑和使用维护都正常的情况下,经过一段时间运转,滚动轴承也会出现疲劳剥落和磨损而不能正常工作。总之,滚动轴承的故障原因是十分复杂的。滚动轴承在运行过程中出现的故障按其振动信号的特征不同主要有磨损类故障和表面损伤类故障,如点蚀、剥落、擦伤等。
准确的包络解调分析是进行滚动轴承故障定量诊断的关键,通过对轴承振动信号直接进行包络解调,特别是当整个轴承系统存在复合故障时,关键的包络谱将出现较大的计算误差,从而导致整个故障诊断的失败。针对滚动轴承故障诊断中,冲击脉冲法(Shock Pulse Method, SPM)结合包络解调技术进行定量诊断误差较大的问题,提出了基于经验模式分解(Empirical Mode Decomposition, EMD)和SPM的滚动轴承故障定量诊断方法。
1 EMD和SPM方法
1.1 EMD方法简介
由美籍华人Huang提出的经验模式分解(Empirical Mode Decomposition, EMD)方法[1]可以将任意非平稳信号x(t)分解为若干个基本模式分量 (Intrinsic Mode Functions, IMFs)ci(t)(i=1,2,…,n)和一个残余分量rn之和,如式(1)所示。
(1)
所谓IMF就是满足以下2个条件的函数或信号:1)在整个数据序列中,极值点的数量和过0点的数量必须相等或最多相差一个;2)在任何一点,信号的局部极大值和局部极小值所定义包络线的均值为0。该方法提出之后被迅速应用于各种领域,在机械设备故障诊断中也有应用[2-10],而本文旨在将该方法应用于滚动轴承故障定量诊断。
1.2 滚动轴承故障定量诊断方法
当滚动轴承发生故障时,在其损伤部位产生的冲击脉冲激励下,安装在轴承箱外部的传感器获得的振动信号中会出现振荡衰减的脉冲响应信号,该信号被各种故障振动频率信号所调制,因此,滚动轴承故障的常用诊断方法是利用包络解调技术,获取故障特征频率对应的包络谱幅值,该幅值直接反应轴承的运行状态,再结合冲击脉冲法 (Shock Pulse Method,SPM)对解调结果进行量化处理,则可以定量识别轴承等部件的损伤程度[8-10]。
SPM是由瑞典SPM Instrument AB公司在上世纪七十年代最先提出的一套系统监测方法。滚动轴承的部件发生故障时,会在运转过程中发生冲击从而引起冲击脉冲。冲击脉冲的强弱反映了故障的严重程度,而其出现的频率则反应了故障对应的位置(轴承内圈、外圈、滚动体及保持架等)。SPM方法正是基于这一原理来评价滚动轴承的运行状态,并且采用了冲击脉冲值这一新的尺度,在实际使用时用分贝值表示。对于不同的轴承,振动脉冲值不仅与轴承的油膜厚度、操作程度有关,还与轴承的几何尺寸、转速有关。为了得到一个衡量各种滚动轴承状态的标准,经过大量的试验研究,SPM方法规定了一个只与轴承工作状况有关的标准分贝值dBn,并给出了dBn的经验公式如式(2)所示
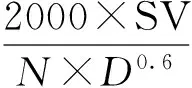
(2)
式中,N表示轴承的转速,单位为r/min;D表示轴承的内径,单位为m;SV表示冲击速度值,单位为ms-1。
可以根据dBn的如下值判断轴承的运行状态:
1) 0≤dBn<21 dB 正常状态,轴承工作状态良好;
2) 21≤dBn≤35 dB 轻微故障,轴承有早期损伤;
3) 35 但是,在工程实际中,通常不止一个载波频率或谐振频率,特别是当轴承出现复合故障时,不同故障的特征频率被不同的载波调制,这样,直接利用包络分析计算的包络谱可能产生误差,从而导致故障诊断的失败,在本文第二节中将具体分析该现象。因此,本文提出利用基于EMD的包络解调分析,结合SPM方法进行滚动轴承故障定量诊断。 2.1 Hilbert解调技术的局限性 Hilbert包络解调是进行解调分析的常用方法,但是它只适合于处理单分量的渐进信号[11],当两个以上的包络信号叠加在一起,或者噪声比较严重的情况下,用Hilbert包络解调的结果往往产生比较大的误差,通过仿真信号的解调分析就能证明该结论。 考虑式(3)所示的仿真信号,它由两个幅值调制信号x1(t)和x2(t)组成,其中两个载波频率分别为fc1=4 000 Hz,fc2=2 000 Hz,两个调制频率分别为f1=80 Hz,f2=60 Hz。 x(t)=x1(t)+x2(t)= (3) 用12 800 Hz的采样频率对该仿真信号进行离散化处理,共采集8 K个数据点,仿真信号及其频谱如图1所示。 由图1可见,两个载波对应的频率附近都出现了相应的调制边频带。由式(3)易知调幅信号x1(t)的幅值a1(t)为: a1(t)=1+0.2sin(2πf1t) (4) 幅值变化频率为f1=80 Hz,x2(t)的幅值a2(t)与之类似,不同的是它的调幅频率为f2=60 Hz。理论上,这两个调幅信号的解调谱幅值应该为0.2。分别对两个调幅信号进行Hilbert解调分析,以x1(t)为例,解调结果如图2所示,其中上图为信号x1(t)的包络,下图为包络谱,包络谱幅值与理论值一致。可见,对单个的调幅信号,Hilbert包络解调技术可以得到正确的结果。 对两个调幅信号叠加而成的仿真信号x(t)做Hilbert包络解调分析,结果如图3所示。 由包络谱可见,解调谱有两个峰值分别等于60 Hz和80 Hz,这说明通过Hilbert包络解调分析可以得到准确的调制频率,但这两个调制频率对应的幅值都明显小于理论值0.2,显然这种情况下得到的包络谱不能反映信号的实际情况。对于轴承故障定量诊断,包络谱中对应故障特征频率处的幅值可以表征故障的存在和严重程度[4],如果信号的包络谱不准确,将影响轴承故障诊断的准确性。 2.2 基于EMD的包络解调分析 由于直接利用Hilbert包络解调技术遇到困难,我们提出了基于EMD的包络解调技术,首先对信号进行EMD分解,然后对得到的各个IMF分别进行Hilbert包络解调。 对式(3)所示的信号进行EMD分解,结果得到三个IMF如图4所示,其中前两个IMFc1(t)和c2(t)分别对应于仿真信号中的两个调幅信号x1(t)和x2(t),而c3(t)能量较小主要是由于分解过程中的能量泄漏和计算误差产生的。 对分解所得的第一个IMFc1(t)进行Hilbert包络解调,结果如图5所示。由图可见,其包络谱幅值正好等于理论值0.2,这说明经过分解之后,Hilbert包络解调结果能更精确地体现信号特征。对分解所得的第二个IMFc2(t)作Hilbert包络解调,也可以得到满意的结果。这说明通过先EMD分解,再对分解所得的IMF进行解调分析,可以对多个调幅信号叠加的信号进行准确的解调分析。 2.3 基于EMD和SPM的滚动轴承故障定量诊断方法 如前所述,SPM方法进行滚动轴承故障定量诊断时,冲击脉冲的强弱反映了故障的严重程度,而冲击出现的频率则反应了故障的位置,所以在进行故障分析之前必须首先求出不同故障对应的特征频率。设滚动轴承的外圈固定,内圈(即轴)旋转,旋转频率为f,轴承的节圆直径为E,滚动体直径为d,接触角为α,滚动体个数为z。假设滚动体与内、外圈之间为纯滚动接触,则滚动轴承的内圈、外圈、滚动体和保持架发生损伤时的故障特征频率计算公式如下: 内圈损伤, (5) 外圈损伤, (6) 滚动体损伤, (7) 保持架损伤, (8) 其中,fi、fo、fb、fc分别称为滚动轴承内圈、外圈、滚动体和保持架故障特征频率。 本文提出的基于EMD的包络解调技术可以对多个调幅信号叠加的信号进行准确地解调分析,再结合SPM方法,便可以进行滚动轴承故障的定量诊断,下面通过一组试验轴承的信号分析验证该方法的实用性和准确性。 在轴承试验台上安装左右两个滚子轴承,左边轴承存在轻微外圈故障,右边轴承存在轻微内圈故障,整个轴承系统存在复合故障,如图6所示。转速为1 477.5 r/min。所用轴承参数为:内径0.04 m,外径0.09 m,滚子直径0.031 16 m,滚子个数为8个。根据式(5)和式(6)分别计算出该轴承内圈故障特征频率为122.11 Hz,外圈故障频率为74.89 Hz。 在右边轴承座处安装加速度传感器,采集轴承振动信号,采样频率为12 800 Hz,采样点数为16 K。轴承振动信号及其频谱如图7所示。 对该信号直接进行包络解调分析,把包络谱幅值作为冲击值,利用式(2)计算对应的分贝值,结果如图8所示。其中图8(a)为轴承振动信号的包络,图8(b)为包络谱换算的标准分贝值。由图可见,在内圈故障特征频率(122.11 Hz)附近分贝值出现峰值18.5 dB,但未超过21 dB,根据SPM法原则判断该轴承运行状态正常,这明显与实际情况不符。 上述分析说明,直接利用包络解调技术处理轴承振动数据,结合SPM方法判断轴承运行状态出现了错误,其主要原因在于该轴承系统存在内外圈复合故障,不同故障产生的调制信号叠加在一起,这种情况下直接进行包络解调所得的包络谱幅值产生了误差,从而导致故障诊断失败。 由于直接利用包络解调分析结合SPM方法进行故障诊断遇到困难,我们提出了基于EMD和SPM的滚动轴承故障定量诊断方法,首先对轴承振动信号进行EMD分解,然后对得到的IMF进行包络解调分析,再结合SPM方法计算对应的振动分贝值。对图6所示的试验信号进行EMD分解,然后对分解所得第一个IMF进行包络解调分析的结果如图9所示。由图可见,内圈故障特征频率处出现了22.12 dB的峰值,根据SPM方法判断该轴承存在轻微内圈故障,这与实际情况相符。 采集左边存在外圈故障的轴承振动信号分析,利用基于EMD的包络解调分析,同样可以得到正确的诊断结果,不同之处在于最大分贝值出现在第二个IMF的包络谱中,这说明内外圈故障特征频率对应的载波频率处于不同频带,即此时的轴承振动信号相当于两个调制信号相叠加,所以直接用包络解调无法得到正确的诊断结果,只有通过基于EMD的包络解调分析结合SPM方法才能进行正确的故障诊断。 本文提出了基于EMD和SPM的滚动轴承故障定量诊断方法,该方法首先对轴承振动信号进行EMD分解,再对得到的IMF做包络解调从而得到准确的冲击值,然后利用SPM方法即可进行滚动轴承故障定量诊断。试验验证结果表明内圈故障特征频率处出现了22.12 dB的峰值,根据SPM方法判断该轴承存在轻微内圈故障,这与实际情况相符。本文方法可以准确地进行滚动轴承故障定量诊断。 [1]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London A: mathematical, physical and engineering sciences. The Royal Society, 1998, 454(1971): 903-995. [2]Cheng Junsheng, Yu Dejie, Yang Yu. Application of support vector regression machines to the processing of end effects of Hilbert-Huang transform[J]. Mechanical Systems and Signal Processing, 2007(21): 1197-1211. [3]祁克玉,何正嘉,訾艳阳.EMD方法在烟机摩擦故障诊断中的应用[J].振动、测试与诊断, 2006(4): 265-268,329. [4]孙书学, 顾晓辉, 吕艳新. 基于经验模式分解的广义互相关时延估计[J]. 探测与控制学报, 2009, 31(2): 5-9. [5]吕艳新, 顾晓辉. 基于时延矢量封闭准则的多传声器降噪方法[J]. 探测与控制学报, 2011, 33(5): 46-51. [6]杨宇,于德介,程军圣,等. 广义解调时频分析方法在调制信号处理中的应用[J].振动与冲击, 2007,26(8):13-16. [7]桂云川, 杨俊安, 吕季杰, 等. 基于经验模态分解的通信辐射源分形特征提取算法[J]. 探测与控制学报, 2016,38(1): 104-108. [8]QIN D, LIU Q, ZHOU L, et al. De-noising methods for power quality signals [J]. East China Electric Power, 2009(5): 21. [9]Hao H, Wang H L, Rehman N U. A joint framework for multivariate signal denoising using multivariate empirical mode decomposition[J]. Signal Processing, 2017, 135: 263-273. [10]Lahmiri S. Comparing variational and empirical mode decomposition in forecasting day-ahead energy prices[J]. IEEE Systems Journal, 2017, 11(3): 1907-1910. [11]姜洪开.第二代小波变换理论研究及其在设备故障诊断中的应用[D].西安:西安交通大学,2006. DiagnosisMethodofRollingElementBearingFaultBasedonEMD NING Jirong1,LIU Yao2 (1.College of Astronautics, Northwestern Polytechnical University, Xi’an 710065, China; 2.Xi’an Aerospace Yuanzheng Fluid Control Co. Ltd, Xi’an 710100, China) Among vibration based fault diagnosis methods for rolling element bearing, the shock pulse method(SPM) combined with demodulation method often misestimates the shock value of characteristic defect frequency. Therefore, a novel method based empirical mode decomposition(EMD) and SPM for rolling element bearing fault diagnosis is proposed in this paper. With this method, the vibration signals are decomposed into several intrinsic mode functions(IMFs), and then demodulation analysis is performed for each IMF so that the exact shock value can be gained, lastly SPM can be used to estimate bearing running state quantitatively with the exact shock value. Simulations and experiments verified that the improved EMD method, combined with SPM and demodulation analysis is efficient and accurate. empirical mode decomposition(EMD); rolling element bearing; fault diagnosis 2017-04-14 宁继荣(1980—),男,陕西合阳人,博士研究生,高级工程师,研究方向:液体火箭发动机总体设计。E-mail:12870006@qq.com。 TB533.1 A 1008-1194(2017)05-0091-052 基于EMD和SPM的滚动轴承故障定量诊断方法
[1+0.2sin(2πf1)]sin(2πfc1)+
[1+0.2sin(2πf2)]sin(2πfc2)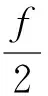
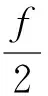
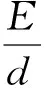
3 试验验证
4 结论

