求解直觉模糊多目标规划的改进遗传算法

杨进帅，王 毅，李 进，文 童，刘占强

(1.空军工程大学防空反导学院，陕西 西安 710051；2.西北大学信息学院，陕西 西安 710069)

求解直觉模糊多目标规划的改进遗传算法

杨进帅1，王 毅2，李 进1，文 童1，刘占强1

(1.空军工程大学防空反导学院，陕西西安710051；2.西北大学信息学院，陕西西安710069)

针对多目标规划获取的参数模糊，求解算法容易早熟收敛和陷入局部最优的问题，提出了求解直觉模糊多目标规划的改进遗传算法。该算法通过定义多目标规划的非隶属度，调节λ参数控制方案选择，执行模拟退火拉马克学习，增强局部搜索能力，指导个体寻找最优值。仿真分析表明，该算法可以灵活地产生多种方案，有效克服早熟收敛和陷入局部最优的问题。

直觉模糊；多目标规划；改进遗传算法；拉马克学习

0 引言

多目标规划是对多个相互冲突的目标的平衡和优化。多目标规划决策环境的不确定，使得获取的参数是不完全的和模糊的。Bellman和Zadeh从事物模糊性的本质出发，提出了模糊规划的概念；此后，Zimmemann提出了模糊多目标规划，S.Orbvsk提出了模糊多目标非线性规划；Atanassov提出的直觉模糊集合(Intuitionistic Fuzzy Sets，IFS)在模糊的基础上增加了非隶属度函数[1-2]，更加细腻地刻画客观世界的本质。

传统算法将多目标转为单目标进行求解，难以得到最优解。目前，国内外学者普遍采用遗传算法、粒子群算法、模拟退火算法等智能算法。遗传算法由于其全局搜索性能突出、随机性和简单易实现等优点，被国内外学者广泛应用于输电网络[3]、交通网络[4]和军事装备[5]等邻域的多目标规划，先后提出了并列选择法，非劣分层遗传算法，基于目标加权法的遗传算法，微遗传算法[6]等改进算法。但是，遗传算法不善于对局部区域精细调整，容易早熟收敛，陷入局部最优，不能有效解决约束优化问题。针对上述问题，本文提出了求解直觉模糊多目标规划的改进遗传算法。

1 直觉模糊多目标规划模型

多目标优化的一般形式为：

(1)

其中，x=(x1,…,xn)，并且xi∈[li,ui]。

Bellman将式(1)转化为模糊约束形式：

(2)

(3)

直觉模糊集在模糊集的基础上，通过非隶属度更加清晰地刻画目标间的关系。设fi(x)={〈x,ufi(x),γfi(x)〉,x∈U}为fi(x)的直觉模糊集，ufi(x)和γfi(x)表示[7]为：

(4)

(5)

(6)

设gj(x)={〈x,ugj(x),γgj(x)〉,x∈U}为约束函数gj(x)的直觉模糊集[8]，ugj(x)和γgj(x)为：

(7)

(8)

dj表示约束gj(x)允许最大的偏移；bj≥0用来调节犹豫度，当bj=0，犹豫度为0，当bj→，犹豫度→1-ugj(x)，bj一般取0～10；λ用来调节gj(x)允许最大的偏移。通过λ调节ugj(x)和γgj(x)的大小，控制对目标函数的约束程度，产生不同的决策方案。取“最小”算子得：

(9)

取fi(x)和gj(x)的 “最小”算子得：

D=M∩S={〈x,uD(x),γD(x)〉,x∈U}

(10)

其中，uD(x)=uM(x)∧uS(x),γD(x)=γM(x)∨γS(x)。

对D在论域U上取“最大”算子，有：

(11)

因此，构建直觉模糊多目标规划模型的一般形式：

(12)

式(12)中，x=[x1，…,xn]，且xi∈[li,ui]。显然，若式(5)中的αi=1，式(8)中的bj=0，则β-α=1-2α，直觉模糊多目标规划退化为模糊规划。因此，直觉模糊多目标规划拓宽了模糊多目标规划的表示范围。

2 改进遗传算法

遗传算法是Holland教授基于遗传选择和自然淘汰的生物进化过程，提出的一种智能算法。其过程为随机产生初始种群，计算适应度值，通过交叉和变异操作进化个体，淘汰适应度值较小的个体，保留适应度值较大的个体，组成子代种群。在迭代进化过程中，遗传算法贪心选择适应度大的个体，导致陷入局部最优，种群容易早熟，无法收敛到全局最优解。如图1所示。

为此，国内外学者通过精英选择策略、自适应交叉和变异等方法改进遗传操作；引入自适应[9]、蚁群算法[10]、直接搜索[11]、模拟退火[12]等算法作为局部搜索策略，精细搜索遗传算法的局部空间。本文基于模拟退火进行局部搜索，采用拉马克学习策略，将学习到的性状直接在个体的基因中编码。

2.1 拉马克学习

拉马克进化理论的观点是“用进废退，获得性遗传”，认为生物体在生存期内存在自身学习的过程，并能将后天学习获得的性状通过基因遗传给后代[13]。这一理论在生物进化中被证明是错误的，却可以将这一理论抽象为一种局部搜索机制，为改进遗传算法提供有益的启发。

学习与遗传进化是生物体适应环境变化的两种不同形式，作用于不同的时间和空间。个体进行学习的过程，即是个体局部搜索的过程。遗传算法是一个全局搜索过程，感知环境缓慢的、整体的变化过程，而学习是全局搜索过程中的某一局部搜索，感知快速的、微小的变化过程。通过学习指导进化方向[14]，跳出局部极值点，引导个体朝向全局极值点进化。如图2所示。

研究表明，模拟退火算法具有通用性和渐进收敛性，能避免陷入局部最优值[15]。本文利用模拟退火算法设计拉马克学习策略，对种群中的个体进行局部搜索。

步骤1:采用n种不同的邻域结构，对种群中个体x在初始温度下进行n(n-1)步执行基于模拟退火的拉马克学习；

步骤2:按下式计算每个邻域的奖励值：

ηi=(fb-fli)/(n(n-1))

式中，fb为进行局部学习前x的适应度值，fli为使用第i(i=1,2,…,n)种邻域结构进行局部搜索后所获得的最佳目标函数值；

步骤3:根据ηi，计算邻域的选择概率：

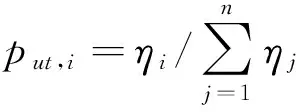
步骤4:采用轮盘赌选择策略确定一个邻域结构，然后对种群的最佳个体在当前温度tk下再进行局部搜索，得到个体x′；

步骤5:基于模拟退火的选择准则，计算学习得到的个体被保留的概率qtk：

步骤6:更新奖励值ηi，若Step4中选择第i个邻域结构，则更新奖励值ηi=ηi+Δηi进行更新，Δηi计算公式如上。

在邻域范围较小的情况下，采用拉马克学习机制跳出局部极值点的可能性更大[16]。本文采用较为简单的邻域结构s={x:|x-x0|<ε}，其中ε<1。

2.2 改进遗传算法

改进遗传算法通过选择父代种群的个体，划分为n个邻域，执行基于模拟退火的拉马克学习，并将学习到的表现型直接在子代个体基因中进行编码，指导个体朝向更好的解移动，并能以一定概率接受差解，保持种群的多样性，避免陷入局部极值。

遗传算法作为全局搜索算法，产生更适应学习的基因，为学习提供更好的初始条件，减小学习的复杂程度。而学习结果能够指导进化的方向，学习到的形状被写入基因。两者的关系见图3所示。

在遗传算法的计算流程基础上，将基于模拟退火的拉马克学习作为一个附加模块，从而改进遗传算法，具体流程如图4。

2.3 求解直觉模糊多目标规划

由于多目标规划的变量较多，二进制编码无法有效描述变量，故选择浮点数编码。采用式(12)作为适应度函数，使用轮盘赌选择、算术交叉和非均匀变异操作，通过优化直觉模糊多目标规划的隶属度和非隶属度函数逼近全局最优解。

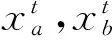
非均匀变异增强算法的局部搜索能力，对原基因作随机扰动，产生两中基因：

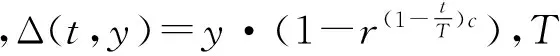
具体求解算法步骤如下：

步骤1：初始化。设定参数，群体规模np，迭代代数k；初始温度tm=t0，降温系数a，群体p(k)；

步骤2：产生初始种群，计算适应度值；

步骤3：对个体进行算术交叉、非均匀变异操作得到种群p1(k)；

步骤4：执行基于模拟退火拉马克学习，搜索局部空间，学习得到的个体直接进入子代种群p2(k)；

步骤5：计算种群p2(k)中个体的适应度值，判断是否满足终止条件。若满足终止条件，则输出最优值的结果，算法结束；若不满足条件，令tm+1=d(tm),m=m+1，降低退火温度，转到Step2。

停止条件为是否进化到最大迭代次数或者收敛到全局最优值。在求解过程中，隶属度函数和非隶属度函数可以通过设置不同的λ参数值进行优化，调节目标函数的适应度值，逐渐逼近到全局最优解。采用比例温度下降法降低模拟退火温度，可以平衡全局和局部搜索速度。

3 仿真及分析

为验证本文算法的有效性，选择在处理器为Intel(R)Core(TM)i7-4790，Windows7旗舰版系统的计算机上，运用Matlab语言编程实现典型的带约束非线性多目标规划，进行仿真比较。

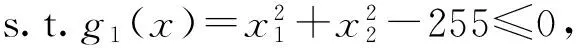
设置参数：种群规模为100，迭代次数为100，交叉概率为0.8，变异概率为0.01；降温系数为0.97，初始温度为90。

实验一：取λ分别为1，0.8，0.6，0.4，0.2，0.1和0，生成不同的约束函数的非隶属度，采用改进遗传算法进行5次重复运算，记录目标函数的最优值，得到表1。相同设置下，求解模糊多目标规划并进行比较，得到表2。

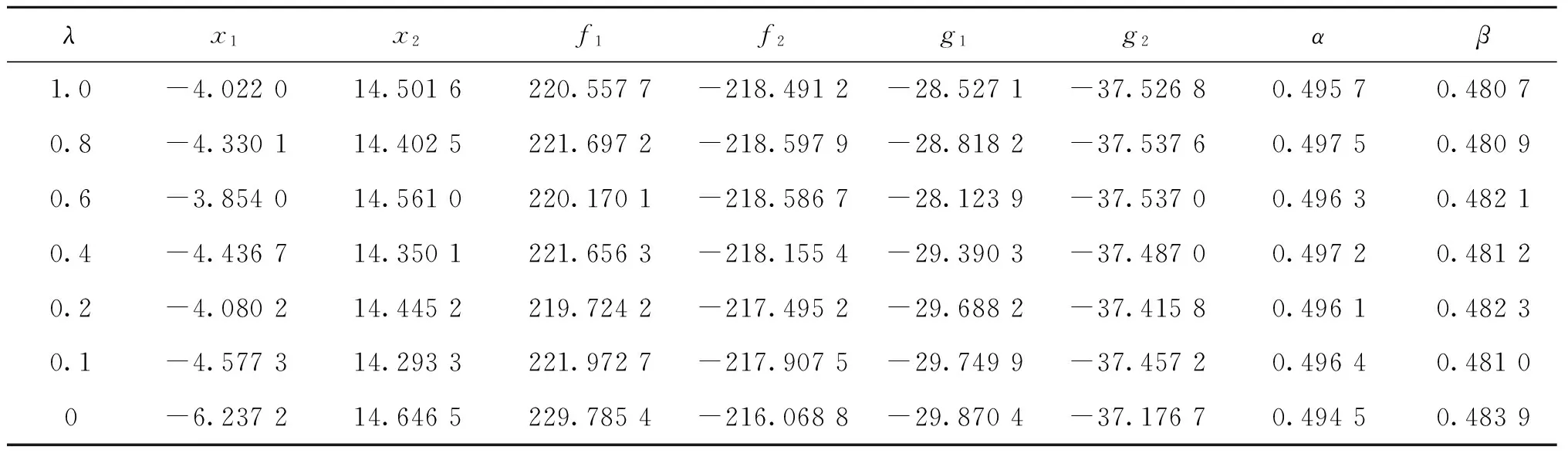
表1 改进遗传算法求解直觉模糊多目标规划

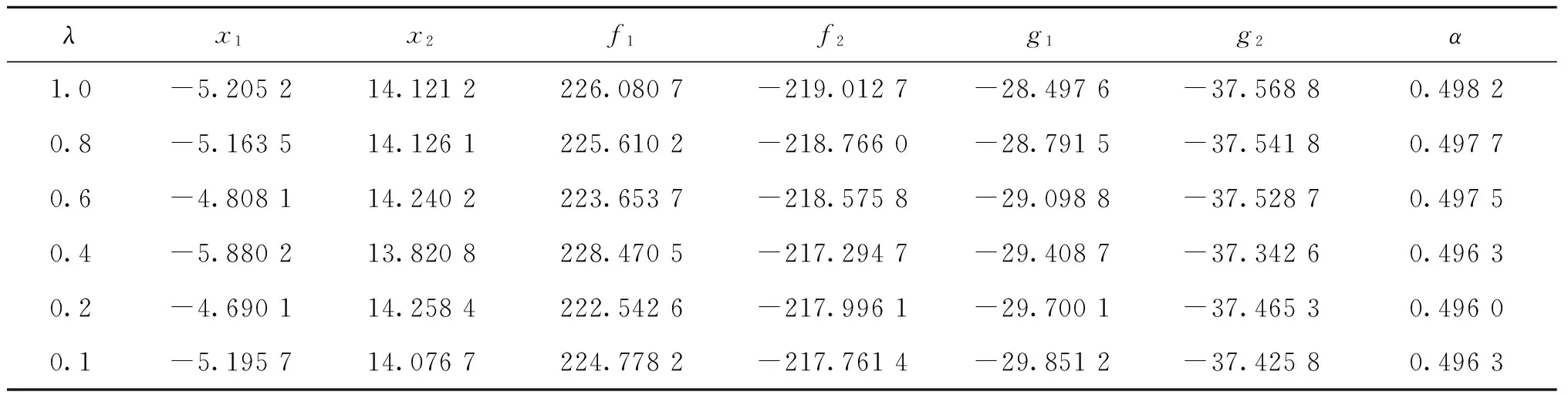
表2 改进遗传算法求解模糊多目标规划

随着λ的减小，目标函数f1和f2的解逐渐增大，越来越逼近最优解。当λ=0时取得最优解，直觉模糊多目标规划模型能清晰地描述各目标之间的关系。与表2相比，f2的值基本相同，但表1中f1的值比表2小3～8，表明直觉模糊多目标优于模糊多目标规划。

实验二：验证算法的收敛性能，并与PSO算法、标准遗传算法进行比较，得到图5。

本文算法执行基于模拟退火的拉马克学习，学习到的结果指导了遗传的进化方向，使其朝着最优值方向迭代，在第35代收敛到最优值，其值大于标准遗传算法，而粒子群算法没有收敛到最优解。

实验三：分析改进遗传算法的种群多样性。使用3倍于每代适应度的均值表征种群的多样性，得到图6。

从图6看出，本文算法的种群均值在10.1～10.7之间，均值变化程度较大。可以认为，该算法求解下既能朝最优值方向进化，又能保持一定比例的较差解，种群的多样性丰富，有效克服了早熟收敛。

4 结论

本文提出了求解直觉模糊多目标规划的改进遗传算法。该算法引入非隶属度，构建了直觉模糊多目标规划，全面地刻画了多目标模糊的本质，更加清楚地区分了各个目标间重要程度；通过λ参数调节约束函数，产生灵活的方案，在决策过程中，可以根据不同的环境和任务需求，选择不同的λ，得到相应的优化方案；执行模拟退火拉马克学习，精细搜索局部空间，并将学习到的性状在后代基因中编码遗传，指导个体朝最优值方向进化，同时以一定的概率接受差解，保持了种群的多样性。仿真结果表明，本文算法求解直觉模糊多目标规划的效益值优于PSO算法和标准遗传算法，能避免陷入局部最优，克服了早熟收敛的问题。

[1]Atanassov K T. Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[2]Atanassov K T, Gargov G. Interal valued intuitionistic fuzzy sets[J].Fuzzy Sets and Systems, 1989,23(31): 343-349.

[3]张宁.配电网多目标经济性优化模型和算法[J].电力自动化设备,2016,32(8):48-53.

[4]孙杨,孙小年,李葆青等.接运公交网络设计的多目标优化模型及遗传变邻域搜索求解算法[J].北京工业大学学报,2014,40(4):535-541.

[5]葛优,刘景萍,赵惠昌,等.基于正交相位编码信号的MIMO雷达测速测距算法[J].探测与控制学报,2016,38(6):80-83.

[6]马小姝,李宇龙,严浪.传统多目标优化方法和多目标遗传算法的比较综述[J].电气传动自动化,2010,32(3):48-50.

[7]徐小来,雷英杰,戴文义.基于遗传算法的直觉模糊多目标规划[J].电光与控制,2009,16(1):31-33.

[8]徐小来,雷英杰,戴文义.基于改进PSO的加权直觉模糊多目标规划[J].系统仿真学报,2009,21(11):3280-3282.

[9]刘文远,刘彬.基于协同进化的自适应遗传算法研究[J].计算机工程与应用,2011,47(14):31-33,36.

[10]邹攀,李蓓智,杨建国，等.基于分层蚁群遗传算法的多目标柔性作业车调度方法[J].中国机械工程,2015,26(21):2873-2879.

[11]王勇胜,梁昌勇,鞠彦忠.多项目环境下time-cost置换问题建模与求解[J].计算机工程与应用,2010,46(20):237-240.

[12]李金忠,夏浩武,曾小荟，等.多目标模拟遗传算法及其应用研究进展[J].计算机工程与科学,2013,35(8):77-88.

[13]王丛佼,王锡淮,肖健梅.基于网格化拉马克学习机制的差分进化算法[J].控制与决策,2015,30(6):1085-1091.

[14]张家奇,陈启军.学习对进化的影响研究及仿真实验[J].系统仿真学报,2007,19(24):5849-5851.

[15]Li Junhui, Chen Xin, Zhu Jinfu. MULTI-OBJECTIVE PROGRAMMING FOR AIRPORT GATE REASSI- GNMENT[J]. Transactions of Nanjing University of Aeronautics & Astronautics,2013,30(2): 209-215.

[16]阎岭,蒋静坪.进化学习策略收敛性和逃逸能力的研究[J].自动化学报,2005,31(6):873-880.

[17]靳飞,单锐.基于局部搜索技术的混合遗传算法[J].辽宁工程技术大学学报(自然科学版),2013, 32(2):269-273.

SolvingIntuitionisticFuzzyMulti-objectionProgrammingbyImprovedGeneticAlgorithm

YANG Jinshuai1, WANG Yi2, LI Jin1, WEN Tong1, LIU Zhanqiang2

(1.Air and Missile Defense College, Air Force Engineering University, Xi’an China; 2.School of Information, Northwest University, Xi’an 710069, China)

An improved algorithm based on operating simulate anneal lamarckian learning was proposed to solve intuitionistic fuzzy multi-objection programming, which aiming at fuzzy obtainable parameter, premature convergence and local optimization. Defining non-membership function of multi-objection programming, adjusting to get more programs, operating simulate anneal Lamarckian learning to search the best individual and enhance the capacity of local search. Through simulation, this algorithm avoided premature convergence and local optimization.

intuitionistic fuzzy; multi-objection programming; improved genetic algorithm; Lamarckian learning

2017-03-21

国家自然科学基金项目资助(61402517)；中国博士后基金项目资助(2013M542331)；陕西自然科学基金项目资助(2013JQ8035)

杨进帅(1993—)，男，陕西旬阳人，硕士研究生，研究方向：智能信息处理与智能决策。E-mail：youngjinshuai@163.com。

TP18

A

1008-1194(2017)05-0096-06