陀螺误差在线建模的递推最小二乘法系统辨识
王佳伟,梁 轲,徐国泰,杨恺华,闫 杰
(1.西北工业大学,陕西 西安 710072;2.机电动态控制重点实验室,陕西 西安 710065)
陀螺误差在线建模的递推最小二乘法系统辨识
王佳伟1,2,梁 轲2,徐国泰2,杨恺华2,闫 杰1
(1.西北工业大学,陕西西安710072;2.机电动态控制重点实验室,陕西西安710065)
针对MEMS陀螺不确定性误差建模方法只能离线进行的问题,提出了陀螺不确定性误差时间序列法在线建模中的迭代递推最小二乘法系统辨识方法。该方法首先通过少量实测陀螺输出数据采用最小二乘法估计出系统参数的粗略值,随后利用新测量到的实时数据采用可重复迭代的递推算法使现有系统参数估计值向其真值逐步逼近。实验室验证结果表明:采用该方法的陀螺不确定性误差模型输出与陀螺真实输出的残差高度近似于白噪声,从统计学角度来说该误差模型能够精确描述陀螺不确定性误差输出特性,该方法可以实现陀螺不确定性误差在线建模。
陀螺不确定性误差;在线建模;递推最小二乘法
0 引言
精确制导炮弹多采用卫星定位和微型惯性组合测量弹道/弹体姿态,MEMS角速率陀螺(以下简称MEMS陀螺)是惯性组合中的重要组成器件,其自身精度直接影响弹体姿态的测量精度。目前提高MEMS陀螺测量精度可以通过改进生产工艺和对其进行误差补偿两种方式实现,而这两种途径所需付出的成本却天壤之别,因此通过对MEMS陀螺误差建模以补偿其测量误差的方法更经济可行。
MEMS陀螺误差主要由确定性误差和不确定性误差构成[1]:对于确定性误差的实验室标定已经非常成熟,一般采用实验方法来获得陀螺的输入输出数据,用多项式定义系统的确定性误差模型;而不确定性误差是一种随机过程,不能用上述方法进行补偿。目前在惯导技术领域被推荐使用的不确定性误差建模方法为PSD法和Allan方差法[2],其中Allan方差法更是IEEE公认的陀螺参数标准分析方法,但这两种方法的估算精度完全依赖于有限且独立的先验数据的个数,是一种离线建模方法;此外,时间序列分析法也是应用广泛的不确定性误差建模方法[3],该方法利用实验法通过白噪声源驱动传递函数以产生与建模对象(MEMS陀螺)具备相同统计特性和谱特性的随机数据,这种根据离线随机数据统计特性建模的思路有别于逐项分析各不确定性误差源的方法,转而针对系统整体输出的统计特性建模,更符合工程实际应用,但它同样是一种离线建模方法。本文针对此问题,提出了陀螺误差在线建模的递推最小二乘法系统辨识方法。
1 研究基础
1.1 时间序列法
目前比较成熟的MEMS陀螺的建模方法是时间序列法,该方法是采用实验法针对一组离线随机数据序列进行时域和频域内的统计特性分析,求出实际物理系统的统计特性,并用自回归滑动平均模型(ARMA模型)进行拟合,经过补偿后与原始输出信号的残差若为类白噪声信号即证明模型拟合精度较高,可以理想描述真实陀螺的不确定性误差[3]。
时间序列法不确定性误差建模是否正确取决于随机数据的一些基本特性:平稳性检验、周期性检验及正态性检验。对这三个基本特性进行检验不仅是分析MEMS陀螺不确定性误差统计特性的重要前提,而且也是建立陀螺不确定性误差模型的重要依据。时间序列法具体步骤如图1所示[4-5]。
如图1所示,经过平稳化处理、周期项分析与提取以及正态性检验得到平稳的随机误差序列。首先,形成ARMA模型对陀螺不确定性误差进行拟合;其次,模型定阶方法选用AIC定阶准则[6],模型的结构采用最小二乘系统辨识方法;最后通过考察拟合残差与白噪声的接近程度来检验模型是否正确。
1.2 最小二乘系统辨识
系统辨识的定义是指在系统输入和输出数据基础上,从一组给定的模型类中确定一个与所测系统等价的模型,是一种采用实验测试法针对某个特定“黑箱”系统的输入/输出(I/O)数据而确定其结构和参数的方法,其中最小二乘法是广泛应用的系统辨识方法,以残差平方和最小为辨识准则[7-8]。
假设系统模型的输出向量形式表达方程如式(1):
YN×1=ΦN×(2n+1)θ(2n+1)×1+ξN×1
(1)
则最小二乘法的系统参数估计结果为:
(2)
可以看到,基本的最小二乘法是一种利用离线I/O数据进行系统参数辨识的方法,可以用于ARMA模型的参数辨识,但其特点是计算量和存储数据量很大,不能用于在线辨识。
2 递推最小二乘系统辨识方法
基于时间序列法的陀螺不确定性误差传统建模方法是在对ARMA模型进行参数辨识过程中采用基本最小二乘辨识方法,只能实现离线建模。
递推最小二乘法在线建模方法的核心思路是采用基本最小二乘法先从少量已知陀螺输出数据中先离线估计出系统参数的粗略值,随后利用新测量到的实时数据采用可重复迭代的递推算法使现有系统参数估计值向其真值逐步逼近。迭代递推步骤如下:
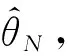
(3)
(4)
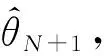

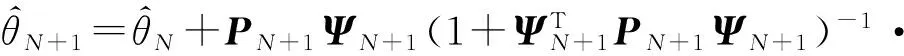
(5)
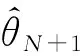
3 实验室验证结果
选用MEMS陀螺在实验室三轴转台的实测数据作为验证对象,考核基于递推最小二乘法的陀螺不确定性误差建模方法的正确性。设定陀螺正转速率400(°)/s的原始输出见图2所示,选择陀螺稳定输出部分经预处理后的结果如图3所示。
经过预处理后的随机信号序列xt,均值μ=2.565,方差σ=0.003 63。首先进行平稳性检验,将随机序列xt分为等长的M个子序列,计算逆序总数A并根据式(1)计算统计量U,取置信度α=0.05,得到表1。

表1 平稳性检验结果
由平稳性检验结果可知|U|=1.644 9 其次进行周期性检验,利用Matlab中的kswelch工具箱可以简便快捷地将随机信号的功率谱计算出来并绘制功率谱密度曲线,因此采用pwelch函数对随机序列xt进行功率谱分析,结果见图4。 可以看到,陀螺随机数据序列功率谱曲线趋势单调,无明显尖峰存在,因此随机采样数据中不具备明显周期信号。 最后进行正态性检验,判断平稳随机数据是否服从正态分布最直接有效的方法是通过统计数据中各个量的概率密度,并绘制这组平稳随机数据的概率密度曲线。利用Matlab中的ksdensity工具箱,绘制概率密度曲线如图5所示,由图可以看出陀螺不确定性误差的概率密度大致服从正态分布特性,通过正态性检验。 表2 ARMA模型系统参数估计及定阶 根据AIC定阶准则选择模型ARMA(1,1)及其所对应差分方程的系统参数,因此可以确定陀螺随机误差模型为: 表3 检验结果 本文提出了陀螺不确定性误差时间序列法在线建模的迭代递推最小二乘法系统辨识方法。该方法首先通过少量实测陀螺输出数据采用最小二乘法估计出系统参数的粗略值,随后利用新测量到的实时数据采用可重复迭代的递推算法使现有系统参数估计值向其真值逐步逼近,最终结合时间序列法建立准确的陀螺不确定性误差模型。实验室验证结果表明:在置信度α=0.05的条件下,基于递推最小二乘法的陀螺不确定性误差模型输出与陀螺真实输出的残差高度近似于白噪声,从统计学角度来说该误差模型能够精确描述陀螺不确定性误差输出特性,该方法可以实现陀螺不确定性误差在线建模。 [1]许江宁,刘强. 陀螺原理及应用[M].北京:国防工业出版社,2009. [2]毛奔,林玉荣. 惯性器件测试与建模[M].哈尔滨:哈尔滨工程大学出版社,2008. [3]王兆密. 基于MEMS陀螺的惯性测量单元的标定与应用[D].镇江:江苏科技大学,2011. [4]徐凯. MEMS陀螺误差补偿的算法研究[D].沈阳:沈阳理工大学,2012. [5]庞存锁,曲喜强,郭华玲. 基于分段处理的线性频率调制信号检测方法[J].探测与控制学报,2016,38(2):60-63. [6]牛春峰. 弹道环境下的陀螺/GPS组合姿态测量方法研究[D].南京:南京理工大学,2012. [7]王秀峰,卢桂章. 系统建模与辨识[M]. 电子工业出版社,2004. [8]燕天,洪飞,邹金龙. 基于短时傅里叶变换与相关解调的参数估计算法[J]. 探测与控制学报,2016,38(2):18-22. RecursiveLeast-squaresMethodofSystemIdentificationinGyroRandomErrorOn-lineModeling WANG Jiawei1,2, LIANG Ke2, XU Guotai2, YANG Kaihua2, YAN Jie1 (1.Northwestern Polytechnical University, Xi’an 710072, China; 2.Science and Technology on Electromechanical Dynamic Control Laboratory, Xi’an 710065, China) Aiming at the problem in method of MEMS angular rate gyro random error on-line modeling, this paper proposed a new algorithm of recursive least-squares method that used in the system identification processing. With this recursive least-squares method, a few known gyro output data were used to roughly estimate system parameters, then newly obtained data were added to the measurement formula using the recursive algorithm in order to make estimated parameters approach to its truth-value. This study indicated that the residual error between outputs of gyro random error model and outputs of real gyro highly approximates white noise, which meant the error model accurately described statistical features of gyro random error and the recursive algorithm realizes on-line modeling. Gyro random error; on-line modeling; recursive least-squares method 2017-02-25 国家自然科学基金项目资助(U1630127) 王佳伟(1984—),男,河北保定人,博士研究生,研究方向:弹道修正。E-mail: wangjiaw0126@163.com。 TJ765 A 1008-1194(2017)05-0036-04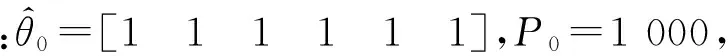


4 结论

