水平摆振下谷物偏析效果的离散元模拟研究

马学东，李亚运，李玲玲，张艳兵，陈 强

(辽宁科技大学机械工程与自动化学院，辽宁 鞍山114051)

水平摆振下谷物偏析效果的离散元模拟研究

马学东，李亚运，李玲玲，张艳兵，陈 强

(辽宁科技大学机械工程与自动化学院，辽宁 鞍山114051)

为了强化厚料层谷物颗粒的分层效果，利用三维离散单元法，结合颗粒空隙填充及动能、动量理论，分析了水平摆振条件下谷粒与短茎秆的分层机理及薄厚料层的分层效果，并采用颗粒体积分数法评价了摆振槽结构改进对厚料层谷物分层的影响。结果表明,在周期性水平摆振作用下，颗粒之间的碰撞使颗粒间缝隙不断变化，同时由于在碰撞时短茎秆的动量远小于谷粒动量，使得短茎秆被排挤到上部空间，而谷粒则渗透至料层下部空隙，最终形成偏析分层。而厚料层谷物因料层密实，底部颗粒间的压力和阻尼较大，使得谷物的动能和垂直方向的动量较薄料层小，导致分层效果较差。在同等参数下，圆柱突起结构振动体的颗粒体积分数相较于光槽振动体颗粒体积分数提高了10%。

水平摆振；谷物；偏析；离散元

颗粒物质是自然界中不同于固体和流体的一种特殊物质形态，由于颗粒系统内部固体粒子的离散性和粒子间相互作用的非线性耗散特征，使得颗粒物质表现出远比普通固体和流体更为丰富的力学特性[1]。特别是在外界动态激励下，颗粒物质会出现对流[2]、尺寸分离[3-4]及几何重构[5-6]等复杂动力学行为。谷物作为颗粒物质的一种，民以食为天，谷物同人类的日常生活密不可分。研究谷物在圆周振动激励下的偏析分层行为具有重要的科学意义和工程应用价值[7-10]。在不同振动条件下颗粒物质表现出不同的分离或分层特征。而现有的颗粒振动分层的研究中大多局限于垂直振动方式[11-13]，对于水平振动方式，也多见于单层颗粒即薄料层的分离行为[14]，而对于水平摆振下，多层颗粒即厚料层颗粒的运动特性及偏析分层行为的研究未见报道；同时,对水平摆振下摆振槽的结构变化对偏析分层效果的影响的研究也未见报道。为了研究厚料层颗粒在水平摆振下的特点并加强其分层效果，本研究使用离散单元法对在水平摆振下稻谷和短茎秆的分层过程进行了模拟研究，分析了其分层机理，以及厚料层颗粒分层效果较差的原因，并根据分析结果对光槽振动体进行了改进，采用颗粒体积分数法对改进效果进行了评价。

1 颗粒模型描述

由于本研究的谷物分层，是对于颗粒物质在水平摆振下相互接触、碰撞、松散、分层等过程的描述，所以采用改进的软球干接触模型[15-16]。由受力分析可知，颗粒运动时主要受自身重力、颗粒间法向分力、切向分力及切向力矩和库伦摩擦力矩的多重作用。当所研究颗粒物质为较大微粒(>1 mm)时，间隙中空气影响可以忽略不计[17]。根据牛顿第二定律，第个颗粒的运动方程为：

(1)

(2)

式中:mi为颗粒的质量，kg；Vi为颗粒i的速度，m·s-1；g为重力加速度，m·s-2；Fn,ij和Ft,ij分别为颗粒i与颗粒j之间的法向接触力和切向接触力，N;Ii为颗粒i的转动惯量，kg·m2；ωi为颗粒i的角速度，rad·s-1；Tt,ij和Tr,ij分别为颗粒i与颗粒j之间的切向力矩和库伦摩擦力矩，N·m。法向分力Fn,ij、切向分力Ft,ij和切向力矩Tt,ij、库伦摩擦力矩Tr,ij等可由离散单元法基本原理求出[18-19]。

2 分层过程数值模拟及分析

2.1参数设定

为了比较薄、厚料层在分层过程中的不同，并分析产生不同的原因。根据实际的物料形状及相关文献[20-22]，将稻谷籽粒和短茎秆分别设置为椭球体及圆筒体，并参照文献[21]及文献[23,24]分别设置谷粒(密度ρ=1 350 kg·m-3)、短茎秆(ρ=100 kg·m-3)和光槽圆筒振动体(ρ=7 861 kg·m-3、内径100 mm、高50 mm、钢板厚度3 mm)的物性参数及接触参数。光槽振动体的振动频率为15 Hz，振幅为15°。薄料层的谷粒和短茎秆分别为1 500粒和1 000粒，厚料层的谷粒和短茎秆分别为1 500粒和1 500粒。

2.2分层过程模拟

在模拟的初始段，谷物与短茎秆在EDEM软件中完成产生，下落并均匀混合于光槽振动体内。随后，物料在圆筒的水平摆振的激励下，不断的进行碰撞、摩擦。10 s时薄料层出现了明显的分层现象，而厚料层谷物与短茎秆则掺杂严重，如图1所示。

图1 10 s时薄、厚料层谷粒和短茎秆的分层模拟结果Fig.1 Snapshots of segregation simulation of paddy rice and short stalks in thin and thick material layer at 10 second

2.3分层过程数据分析

对于整个分层过程(0～10 s)而言，分层初始的前段时间内(0至1 s时)，谷粒和短茎秆主要完成产生、下落、静置等活动，所以本研究主要对1～10 s内的谷物分层行为进行记录分析。

颗粒之间的间隙是谷物分层的前提，而谷物之间的接触次数能直观地表现出颗粒间隙的变化。在相同的混合密度下，颗粒接触次数越多表明颗粒间隙越小，接触次数越少表明颗粒间隙越大。由图2可以看出，谷物颗粒的接触次数随振动不断变化，呈波动状态，说明分层过程中颗粒间隙不断变化。厚、薄料层谷物在分层初始阶段，谷粒与短茎秆的混合密度大体相同，颗粒总数厚料层为薄料层的1.2倍，接触次数厚料层却约为薄料层的2.2倍，说明单位数量的谷粒与短茎秆厚料层的接触次数比薄料层的多，即厚料层的料层更为紧密。

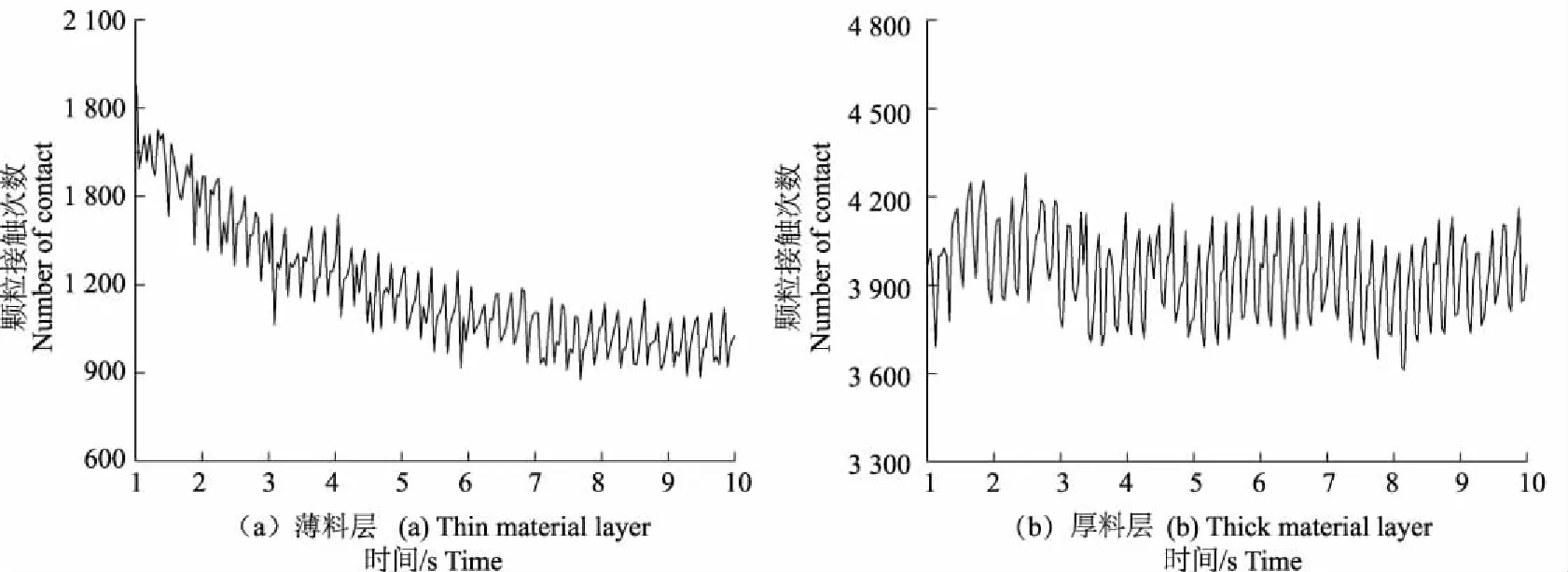
图2 薄、厚料层谷粒和短茎秆的接触次数随时间变化的曲线Fig.2 The curves of contact numbers versus time between paddy rice andshort stalks in thin and thick material layer

在分层过程中，谷物与圆筒、谷物与谷物之间的碰撞与摩擦会引起谷物动能的不断变化，而谷物颗粒动能的变化又直接影响谷物的分层速率和效果。由图3可以看出，相对于质量较小的短茎秆颗粒，质量较大的谷粒的平均动能远大于短茎秆的平均动能，说明谷粒颗粒获得能量远大于短茎秆颗粒获得的能量。在分层过程中，谷粒颗粒主导运动形式。在分层过程中谷物颗粒的动能随振动不断变化，这是由于在水平摆振过程中，谷粒和短茎秆在摩擦力的作用下将展现出一定的流体特征。当光槽振动体由静止向某一方向转动时，物料以轴线为中心，沿圆周方向运动，此时颗粒群运动较为规则。筒内的颗粒系统呈现类似层流的运动形态，此时颗粒与振动体的摩擦力为动力，颗粒群动能逐渐增大。当光槽振动体反向转动时，颗粒与振动体的摩擦力为阻力，谷粒和短茎秆在圆筒中被打乱，各颗粒间出现碰撞、松散、混掺等较激烈的力学行为，造成颗粒间隙改变，颗粒群呈现类似紊流的运动形态，颗粒的动能被大量消耗。对比2幅图可以看出，薄料层谷粒的平均动能的波峰约为厚料层的1.5倍，且厚料层谷粒的平均动能的波谷接近为0。这说明厚料层谷粒在分层过程中单个颗粒具有的动能较小，且经过紊流运动形态后谷粒颗粒接近于静止状态。

图3 薄、厚料层物料颗粒平均动能随时间变化的曲线Fig.3 The curves of average kinetic energy versus time of materialparticles in thin and thick material layer

物料颗粒竖直方向上的平均动量，可以直观地反映出分层过程中谷粒与短茎秆上下运动的趋势。由图4可以看出，薄、厚料层谷粒的平均动量均远大于短茎秆颗粒，且谷粒向下平均动量均大于向上动量，说明在谷粒与短茎秆碰撞时，短茎秆容易被挤走，而谷粒则更容易向料层底部运动。厚料层竖直方向上的平均动量不及薄料层的，说明厚料层的谷物在竖直方向上的位置交换不如薄料层的活跃。

以上分析可以看出，在水平摆振作用下，颗粒之间接触、碰撞、料层的相互作用使得颗粒间隙不断变化，加之料层较薄底部颗粒受到的压力与阻尼较小，这就为谷粒和短茎秆的位置更换创造了条件。在重力的作用下，物料颗粒有向料层下部运动的趋势。当颗粒碰撞发生时，由于短茎秆颗粒所含能量、动量远小于谷粒，其更容易向外部自由空间移动，而向下动量较大的谷粒渗透至料层下部空隙，底部空隙逐渐被谷粒填满，料层中的短茎秆不断受到排挤，移动至料层上部，最终形成了谷粒在下短茎秆在上的分层效果。

而在厚料层谷物中，料层相对紧密，底部颗粒间的压力和阻尼较大，使得在相同的外部激励下谷物所具有的动能、动量小，导致谷物颗粒在相互碰撞时颗粒间的间隙变化小，使得底部短茎秆在物料碰撞的过程中难以突破上层物料进入外部自由空间，从而阻碍了谷粒渗透至料层下部的空隙，致使谷粒和短茎秆主要在水平方向上振动，最终使厚料层谷物的分层效果较差。

3 振动体结构对颗粒分层的影响

由上述分析可以看出，厚料层颗粒在光槽振动体中的分层效果远不如薄料层的分层效果，但厚料层颗粒的分层行为在工程应用中更具有实际意义，所以有必要进一步探讨厚料层颗粒分层效果的优化方法。根据上面的分析并考虑到水平摆振时，不同结构的振动体提供给物料的能量、动量不同，而得到不同的分层效果。现对光槽振动体作如图5所示的结构改进，以达到松散料层，快速分层的目的。图5中2个圆筒的大小和材料与光槽振动体的完全一致。其中图5(a)的圆筒底部添加了3个圆头矩形凸起(长L=15 mm，宽B=4 mm，高H=3 mm，圆角半径R=1 mm)，该矩形突起的底面中心到圆筒底面圆心的距离均为22.5 mm，且相邻的2个矩形突起之间的夹角为120o；图5(b)的底部在半径为30 mm且与圆筒内壁同轴心的圆上均匀分布有6个圆柱凸起(直径D=4 mm，高H=3 mm，圆角半径R=1 mm)。另外为了强化料层中心部位颗粒的活跃度，进一步加强厚料层颗粒的分层效果，在两个圆筒的底部中心位置分别添加了一个圆柱突起(直径D=4 mm，高H=3 mm，圆角半径R=1 mm)。

为定量描述颗粒在不同振动体中的分层效果，本文采用体积分数法作为衡量分层速度的标准。若颗粒体系由M种粒级的颗粒组成，空间s内t时刻，第B种颗粒的体积分数φB(s,t)的表达式如式3所示：

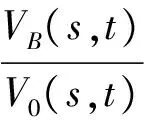
(3)

式中：VB(s,t)为空间s内t时刻第B种颗粒的体积；V0(s,t)为空间s内t时刻M种颗粒的总体积。

图5 改进结构后的振动体Fig.5 Vibrators with different geometry

图6是通过统计分析得到的不同振动体中短茎秆体积分数的变化曲线(振动频率为15 Hz、振幅为15°、统计区域为图6中点划线选择框所在区域，为充分显示不同结构振动体对分层效果的影响将模拟时间延长至20 s)。从图6可以看出，在水平摆振的作用下，光槽振动体短茎秆的体积分数随时间的变化不大 ，在20 s模拟完成时仅比初始时增加了0.01且为0.56，说明谷粒与短茎秆混掺较

图6 不同结构振动体对分层效果的影响Fig.6 Effects of vibrator geometry on granular segregation

多，分层效果不好。当振动体选用圆柱凸起结构时，短茎秆的体积分数随时间明显增大，尤其在1～5 s时增长迅速，20 s时达到0.66且曲线仍略有上升趋势，这说明圆柱凸起结构提供了足够用于颗粒摩擦、碰撞、分层的能量，起到了松散物料的目的，最终得到了较好的分层效果，且分层过程迅速。当选用矩形凸起结构振动体时，短茎秆的体积分数在1～4 s时与圆柱凸起结构振动体的变化规律基本一致，但在4 s以后略低于圆柱凸起结构振动体的体积分数。分析是由于矩形凸起结构振动体也可以提供足够的分层的能量，但是由于矩形凸起存在死角阻碍了颗粒在水平摆振下的运动，所以分层效果不如圆柱凸起结构。

4 结论

1) 物料的主要能量来源于振动和摩擦，振动改变了颗粒间隙，为谷粒和短茎秆的位置交换提供前提条件。由于短茎秆的能量和动量远小于谷粒，碰撞时短茎秆更容易向外部自由空间运动，此时总体向下动量较大的谷粒移动并填充至料层下部空间，短茎秆在不断排挤中被移至料层上部，形成最终的分层效果。

2) 在光槽振动体条件下薄、厚料层谷物的分层效果具有很大的差异。薄料层谷物颗粒的松散性好、分层速度快、分层效果明显，而厚料层则因为料层紧密、底层颗粒压力大，阻碍了底部短茎秆向外部空间的移动，使得底部物料没有足够的空隙让上层谷粒渗透，导致厚料层的分层效果不明显。

3) 振动体结构对谷物分层有较大的影响。相同振动参数的水平摆振作用下，光槽振动体的分层速度慢且效果较差。矩形凸起结构振动体虽然可以使谷物快速进入分层状态，但因其结构存在死角，使得其分层效果并不理想。圆柱凸起结构振动体即能为谷物分层提供充足的能量，又避免了结构死角的问题，使得其分层速度较快，分层效果较理想。

[1] 蔡慧. 垂直激励下环形颗粒系统中的波动与流动[D]. 南京：南京大学, 2015.

[2] KNIGHT J B, JAEGER H M, NAGEL S R. Vibration-induced size separation in granular media: the convection connection[J]. Physical Review E, 1993, 70: 3728-3731.

[3] ROSATO A, STRANDBURG K J, PRINZ F, et al. Why the Brazil nuts are on top: Size segregation of particulate matter by shaking[J]. Physics Review Letters, 1987, 58(10): 1038-1040.

[4] 姜泽辉, 荆亚芳, 赵海发, 等. 振动颗粒物质中倍周期运动对尺寸分离的影响[J]. 物理学报，2009, 58(9): 5923-5929.

[5] OSAMU S. Dilatancy, buckling, and undulations on a vertically vibrating granular layer[J]. Physical Review Letters, 2005, 72(5): 1-7.

[6] GARCIMARTIN A, MAZA D, ILQUIMICHE J L, et al. Convective motion in a vibrated granular layer[J]. Physical Review E, 2002, 65(2): 1-5.

[7] 赵永志, 江茂强, 郑津洋. 巴西果效应分离过程的计算颗粒力学模拟研究[J]. 物理学报, 2009, 58(3): 1812-1818.

[8] BURTALLY N, KING P J, SWIFT M R. Spontaneous air-driven separation in vertically vibrated fine granular mixtures[J]. Science, 2002, 295: 1877-1879.

[9] MULLIN T. Mixing and demixing[J]. Science, 2002, 295: 1851-1860.

[10] KENNEDY D, NORMAN C. What don’t we know [J]. Science, 2005,309: 75-79.

[11] 梁宣文, 李粮生, 侯兆国, 等. 垂直振动作用下二元混合颗粒分层的动态循环反转[J]. 物理学报, 2008, 57(4): 2300-2305.

[12] 史庆藩, 阎学群, 厚美瑛, 等. 振动混合颗粒形成的反巴西果分层及其相图的实验观测[J]. 科学通报, 2003, 48(4): 328-330.

[13] DURAN J. Sand, powder, grains[M]. New York: Springer, 2000.

[14] AUMA TRE S, KRUELLE C A, REHBERG I. Segregation in granular matter under horizontal swirling excitation[J]. Physics Review E, 2001, 64(4): 1-4.

[15] ODA M, IWASHITA K, KAKIUCHI T. Importance of particle rotation in the mechanics of granular materials[M]. Rotterdam: Balkema, 1997

[16] ZHU H P, ZHOU Z Y, YANG R Y, et al. Discrete particle simulation of particulate systems: Theoretical developments[J]. Chemical Engineering Science, 2007, 62(13): 3378-3396.

[17] ZEILSTRA C, HOEF M A, KUIPERS J A M. Simulation of density segregation in vibrated beds[J]. Physics Review E, 2008, 77(3): 1-13.

[18] 赵永志, 江茂强, 徐平, 等. 颗粒堆内微观力学结构的离散元模拟研究[J].物理学报, 2009, 58(3): 1819-1825.

[19] 赵永志, 程易. 水平滚筒内二元颗粒体系径向分离模式的数值模拟研究[J].物理学报, 2008, 57(1): 322-328.

[20] 李洪昌, 李耀明, 唐忠, 等. 基于EDEM的振动筛分数值模拟分析[J]. 农业工程学报, 2011, 27 (5): 117-121.

[21] 贾富国, 韩燕龙, 刘扬, 等. 稻谷颗粒物料堆积角模拟预测方法[J]. 农业工程学报, 2014,30(11): 254-260.

[22] 李菊, 赵德安, 沈惠平, 等. 基于DEM 的谷物三维并联振动筛筛分效果研究[J]. 中国机械工程, 2013, 24(8): 1018-1022

[23] SAKAGUCHI E, SUZUKI M, FAVIER J F, et al. Numerical simulation of the shaking separation of paddy and brown rice using the discrete element method[J]. Journal of Agricultural Engineering Research, 2001, 79(3): 307-315.

[24] DAS H. Separation of paddy and rice on an oscillating tray type separator[J]. Journal of Agricultural Engineering Research, 1986, 34(2): 85-95.

(责任编辑：蒋国良)

Discreteelementsimulationofgrainsegregationeffectunderhorizontalpendulumoscillations

MA Xuedong, LI Yayun, LI Lingling, ZHANG Yanbing, CHEN Qiang

(School of Mechanial Engineering and Automation ,Liaoning University of Science and Technology, Anshan 114051, China)

For strengthening layering effect of thick-layer grain particles, a simulation study for segregation process of grains and short stalks when plain trough cylinder vibration body is under horizontal pendulum oscillations was carried out using the three-dimensional discrete element method. And the grain segregation mechanism was analyzed in detail based on the theory of gap filling, kinetic energy and momentum of the grain particles. By comparing different contacting times, kinetic energy and momentum of the particles in the segregation process of thin and thick material layer, we analyzed the reason of the poor layered effect of the thick material layer. The analysis results show that：under the action of periodic horizontal pendulum oscillations，the collision between particles change the gap of grain particles，which provides precondition for layering, and the collision and friction between particles and vibration body provide energy for layering. Because the energy and momentum of the short stalks is far less than the grains during the collision of the grains and short stalks, the short stalks are crowded to the upper space, and the grains are permeated to the gap of the lower part of the material layer, and then the layering is formed. Meanwhile, thick material layer is dense, and pressure and damping are bigger between bottom grains, which makes kinetic energy and momentum of vertical direction of the grains less than thin material layer, causing a poor layering effect. The particle volume fraction of the vibration body of adding cylindrical bump structurere is improved by 10% compared to that of the light slot vibration body after improvement.

horizontal pendulum oscillations; grain; segregation; discrete element

2017-02-30

辽宁省高校创新团队支持计划(TL2015014)

马学东(1965-)，男，内蒙古赤峰人， 副教授，博士，主要从事颗粒物质动力学行为研究。

1000-2340(2017)05-0687-06

TD452

A