装备k/N系统保障备件配置优化模型*

付冰，刘福胜，闫旭

(装甲兵工程学院 技术保障工程系，北京 100072)

装备k/N系统保障备件配置优化模型*

付冰，刘福胜，闫旭

(装甲兵工程学院 技术保障工程系，北京 100072)

备件是装备保障中重要的保障资源之一，是保证装备系统良好战备状态和恢复战斗力的重要因素。针对预防性维修中k/N系统备件配置模型不合理导致保障效益低下的问题，提出一种新的备件配置优化模型。模型考虑不同的故障类型对备件配置的影响，以配置备件数目最小为目标函数，以新构建的使用可用度模型和保障费用模型为约束条件，利用惯性权重递减的改进粒子群算法来提高模型求解效率。最后给出一个算例，结果表明模型能够合理的进行备件配置，给出最优备件配置方案，获取最佳的经济效益，提高装备系统保障效能。

k/N系统；保障备件；使用可用度；保障费用；配置优化；改进粒子群算法

0 引言

备件是装备保障的重要保障资源之一，备件的配置优化在保证装备战备完好性的情况下对备件进行合理的配置，同时获得最佳的综合经济效益，为保障人员提供决策。在备件优化配置问题研究中，专家们通过运用的算法和针对的系统都各有不同。例如，文献[1]运用遗传算法和神经网络相互结合建立电子装备备件优化模型，文献[2-4]利用改进的PSO算法在不同的约束条件下对备件配置建立优化模型，文献[5]采用改进MOPSO算法，以备件保障能力和保障费用作为目标函数，对高维、非线性的多级备件配置问题进行优化。文献[6]在多级维修下考虑装备的使用可用度或保障费用来所为约束来研究装备系统的备件配置优化，文献[7]改进了传统的分层编辑算法，建立可用度模型优化备件库存配置。

k/N系统中包含的单元可以是相同的，也可以是不同的，各单元可以是独立的，也可以有一定的关联，当系统中失效单元达到一定的数量之后，维修单位才会对系统进行维修。k/N系统具有系统大，设备多，维修任务重的特点，但是它提高了系统整体的可靠性和使用可用度，因此被广泛应用在多种武器装备系统中，例如飞机发动机系统，舰船、相控阵雷达系统等。根据预防性维修策略对k/N系统进行合理的保障资源配置，可以减少维修工作量，降低保障费用，同时可以提高装备系统的战备完好性水平。针对其不同的系统特征，文献[8]估算了包含不同单元的k/N系统的可靠度，文献[9]建立了两级维修模式下k/N系统的使用可用度模型，文献[10]在k/N系统可靠性分析问题上也进行了深入的研究。文献[11]采用改进的边际分析法对舰载k/N系统展开研究，解决了维修时机和备件携行量的联合优化问题。文献[12]对可修部件建立模型开展联合优化。

1 问题描述及假设

本文以某一装备的可修复k/N系统展开研究，在装备使用过程开始阶段，所有N个不同单元部件都是没有故障的，本文涉及的装备系统中N个不同部件的寿命周期均服从参数为λ的指数分布，但其他性能、费用以及补给状况不同，且各部件之间不考虑故障的相互关系，即互相独立同分布。只要系统中的故障件数n≥N-k+1，则装备因故障彻底停机。对于装备来说，维修主要包括预防性维修和修复性维修。在实际的使用过程中，如果到达规定的预防性维修周期时间T时仍没有产生故障，则进行预防性维修；如果在这个周期内部件因为故障导致停机，则进行修复性维修。一般情况下，预防性维修的间隔期是固定的，用装备重要功能产品的最优维修间隔期来确定。为确保装备的可用性，在预防性维修期间除关键部件之外的大量产品根据其技术状态来决定时都更换或者维修。

装备的所有部件都应该依据部件本身的技术状况来确定实施维修活动。本文中模型建立通过0-1决策变量来判断是否进行预防性维修。装备综合保障理论中指出，对已确定的部件需要针对其故障模式和影响进行修复性维修决策[13]。故障形式不同，采取的修理方式也就不一样。因此本文根据部件的不同的故障模式将修复性维修活动分为2类：一类是该部件的故障对装备的功能影响较小，在使用现场就能进行简单的维修，不进行更换；另一类是该部件的故障对装备功能有较大的影响，必须进行相应的换件修理，这样便会产生保障延误时间。那么，部件i在第j次预防维修周期中t时刻出现这2类故障的概率Fi1(tj)，Fi2(tj)为

Fi1(tj)=αi1[1-e(-λitj)]，

(1)

Fi2(tj)=αi2[1-e(-λitj)]，

(2)

式中：αi1,αi2为部件发生两类故障模式的频数。

为了建立模型，假设部件经过维修后性能如同新部件，能立即转为备用件使用；为保障系统的故障件及时的更换，库存备用件Mi0个，在装备系统进行维修阶段，维修人员用备用件更换故障件，更换时间独立同分布，均服从参数为ρ的指数分布。当使用一个备件后，备件的库存量减一。当备件库存紧张，不能及时进行更换时，需要临时调用备件，产生备件延误时间。在更换备件后，维修人员对故障件进行维修，则配置Hr个维修人员，故障件的修复时间独立同分布，服从参数为μ的指数分布。

2 备件优化模型建立

为了构建装备使用可用度和备件保障费用的模型，以下为模型所需要的参数：

T：已知常数，表示所研究的装甲装备的某一给定的时间段；本文是研究在给定时间T内的装甲装备使用可用度与维修保障的优化模型。

Tj：装备在第j个预防性维修周期。

tir1：第i个部件发生第1类故障的维修时间。

tir2：第i个部件发生第2类故障的维修时间。

λi：装甲装备系统第i个部件的故障率。

Rij(t)：系统在第j个维修间隔期内的可靠性函数，其表达式为

(3)

tip：装备第i个部件的平均预防性维修时间，为常数。

Pij为0-1决策变量，表示装备第i个部件在第j个维修周期内进行预防性维修与否，Pij=0表示进行，Pij=1表示不进行。

tiσ：表示部件在第2类故障维修中，由于缺件产生的平均后勤延误时间，本文忽略因维修人员产生的延误时间，即只考虑因缺少备件而产生的平均延误时间，表达式为

tiσ=Fi2(t)tpi(1-PiB)，

(4)

式中：tpi为获取备件的周转时间，为常数；PiB为第i个备件的平均备件保障概率[14]，其表达式为

(5)

式中：t0为日历时间与停机维修时间的差值；Bi(g)为第i个部件进行第g次换件维修开始时可用的备件数目，备件的更换服从参数为ρ的指数分布；Mi0为维修单位备有原有备件数量。

2.1使用可用度模型的构建

装备在第j个预防性维修周期期间的可用度为

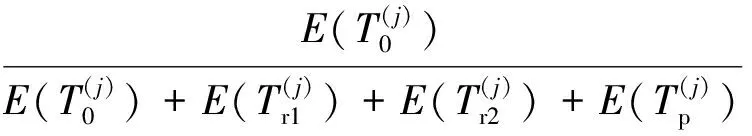
(6)

期间装备工作时间的期望值为

t.

(7)

部件在第j个预防性维修周期内进行预防性维修时间的期望值为

(8)

部件在第j个预防性维修期间发生第1类故障后进行维修所需要时间的期望值为

(9)

在进行第2类故障维修时，若可用备件数目充足，即Bi(g)≥1时，则有

(10)

若可用备件不充足，则产生因备件调配产生备件延误时间，即装备在第j个预防性维修周期期间出现第2类故障需要进行维修的时间期望值为

(11)

根据备件消耗过程可以得到，Bi的初始值是Mi0，Dr为维修结束后修复的故障件个数，在预防性维修期间，将更换下来的可修复故障件进行维修，维修结束后故障件数目自动转为备件数目，则本次Bi等于上次维修后剩余的备件再加上预防性维修期间修复的故障件个数，又因为存在没有故障件可修的情况，所以Bi不可能超过Mi0，则有

Bi(1)=Mi0，Bi(g)=min{[Bi(g-1)-1]++

Dr,Mi0},g=1,2,…,∞，

(12)

式中：[x]+=max{x,0}。

由于各部件都服从故障为λi的指数分布，因为指数分布“无记忆性”，则第i个与第i+1个故障间隔时间服从参数为(N-i)λi的指数分布，则Hr个维修人员在2次维修期内可修复的故障件个数Dr为

i=1,2,…,n-1.

(13)

将上述各式代入式(6)得装备在某一预防性维修周期Tj内的使用可用度为

(14)

则系统在某一预定时间T内的使用可用度为

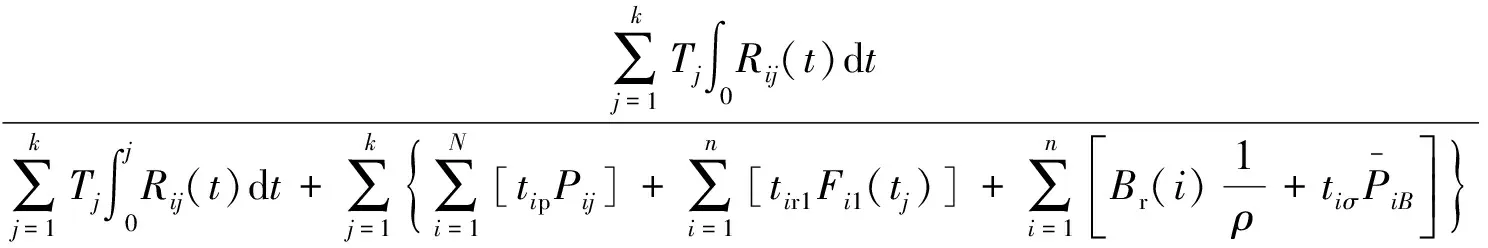
(15)

2.2构建维修保障费用模型

在装备各级保障管理中，除了关注装备的战备完好性之外还应考虑装备维修的保障费用这项指标，必须兼顾使用可用度最大和保障成本最低的条件。

装备在第j个预防性维修周期内产生的维修保障费用所包含的内容有：第i个产品的预防性维修费用Cip，发生第1类故障产生的费用Cr1(T(j))，产生第2类故障的维修费用Cr2(T(j))，单位备件成本Cps，单个故障件储存成本Cpg，单位时间内单个维修人员的成本Crh。

装备部件在第j个维修性周期内的预防性维修的期望维修费用为

(16)

发生第1类故障产生的维修费用Cr1(T(j))为

(17)

发生第2类故障的期望维修费用Cr2(T(j))为

(18)

备件购置成本：

CPS=Mi0Cips,

(19)

预防性维修期间备件的存储成本：

CST=M0Cpg+TjDrCpg.

(20)

第j个预防性周期内维修人员费用：

CH=HrTjCrh，

(21)

将以上各式相加即得，在第j维修周期重装备的维修费用C(T)为

C(T)=Cr1(T(j))+Cr2(T(j))+

Cp(T(j))+CPS+CST+CH.

(22)

则系统在某一预定时间T内的总维修费用为

Cp(T(j))+CPS+CST+CH]，k为整数.

(23)

2.3装备系统备件配置优化建模

以装备系统的保障费用和使用可用度作为目标函数，约束条件是装备部件的使用可用度不低于最低值Asys和保障费用不高于最高值Csys，找出备件库存的最优数量，使得装备的使用可用度在达到最大的同时保证保障费用为最小，则模型的数学表达式为

(24)

3 基于粒子群算法的备件优化模型求解

3.1算法介绍及粒子表示

粒子群算法是基于群体的随机优化技术。基本参数为：粒子群有n个粒子组成X=(X1,X2,X3,…,Xn)，第i个例子表示一个D维向量Xi=(xi1,xi2,…,xiD)T，其速度为υi=(υi1,υi2,…,υiD)T，个体极值为Pi=(Pi1,Pi2,…,PiD)T全局极值为Pg=(Pg1,Pg2,…,PgD)T。该算法采用群体进化适应度函数来评价优化结果，算法中的每一个粒子的适应值都有一个适应度函数与之对应，粒子在解空间中的移动速度和位置具有速度和位置两种属性来表示，与此同时，粒子的位置坐标的适应度函数值反映了粒子的好坏程度。每一次迭代中粒子通过对本身最优解和群体的当前最优解不断的进行更新，并且再根据所有粒子的经验进行动态的调整，更新位置和速度所用到的公式为

(25)

式中：c1，c2为权重系数；ξ，η为[0,1]区间均匀分配的随机值。

在基本粒子群优化算法基础上，学者向式(25)引进了惯性权重因子ω，即

(26)

权重ω影响微粒的局部寻优能力和全局寻优能力[15]。由于较大的权重因子对跳出局部最小点更有益处，更方便在全局搜索，相反较小的权重因子有利于精准的局部搜索，所以可以采用线性变化的权重让权重从最大值ωmax线性减小到最小值ωmin。随算法迭代次数变化公式为

(27)

式中：ωmax，ωmin为最大和最小惯性权重；t为当前迭代步数；tmax为最大迭代步数。

3.2适应度函数构造

适应度函数是评价群体中个体优劣势，引导粒子群移动的方向与速度。根据备件使用可用度和维修保障费用约束模型，要求可用度最大和维修保障费用最小2个约束，要求最终达到备件数目最小，本文确定的适应度函数为

(28)

3.3算法求解过程介绍

粒子群算法求解过程如图1所示。

图1 粒子群算法求解过程Fig.1 Flow chart of particle swarm optimization algorithm

(2) 计算每个微粒的目标函数值，即适应度。选出适应度值最好的粒子位置pbest作为种群的位置gbest。

(3) 更新粒子的位置和速度。

(4) 计算更新后粒子的适应度值，并与之前经历过的最好位置pbest的适应度进行对比，如果更好，则充当该粒子新的最好位置pbest。

(5) 将所有粒子的适应度与种群所经历过的最好位置相比，更新出新gbest的极值。

(6) 检查终止条件，判断最优解是否停止变化，如果没有，则返回(3),如果判断已满足预先设置的条件，则停止迭代，并输出最优解。

4 案例分析

假设装备某系统由5个不同部件构成，对应备件的参数，如表1所示，表中时间单位均为h，费用单位均为元。

若故障件个数n≥3，则系统停机开始进行维修。设Asys=0.76，Csys=25 000 元，T=1 000 h，Tj=250 h，Hr的值取2。本文利用Matlab编写粒子群算法程序，种群规模取10，迭代次数为100代，最大惯性权重ωmax取0.9，最小惯性权重ωmin取0.4，加速系数c1，c2取为2.0，更快的收敛于最优值，提高工作效率，获得最终适应度变化曲线如图2所示。

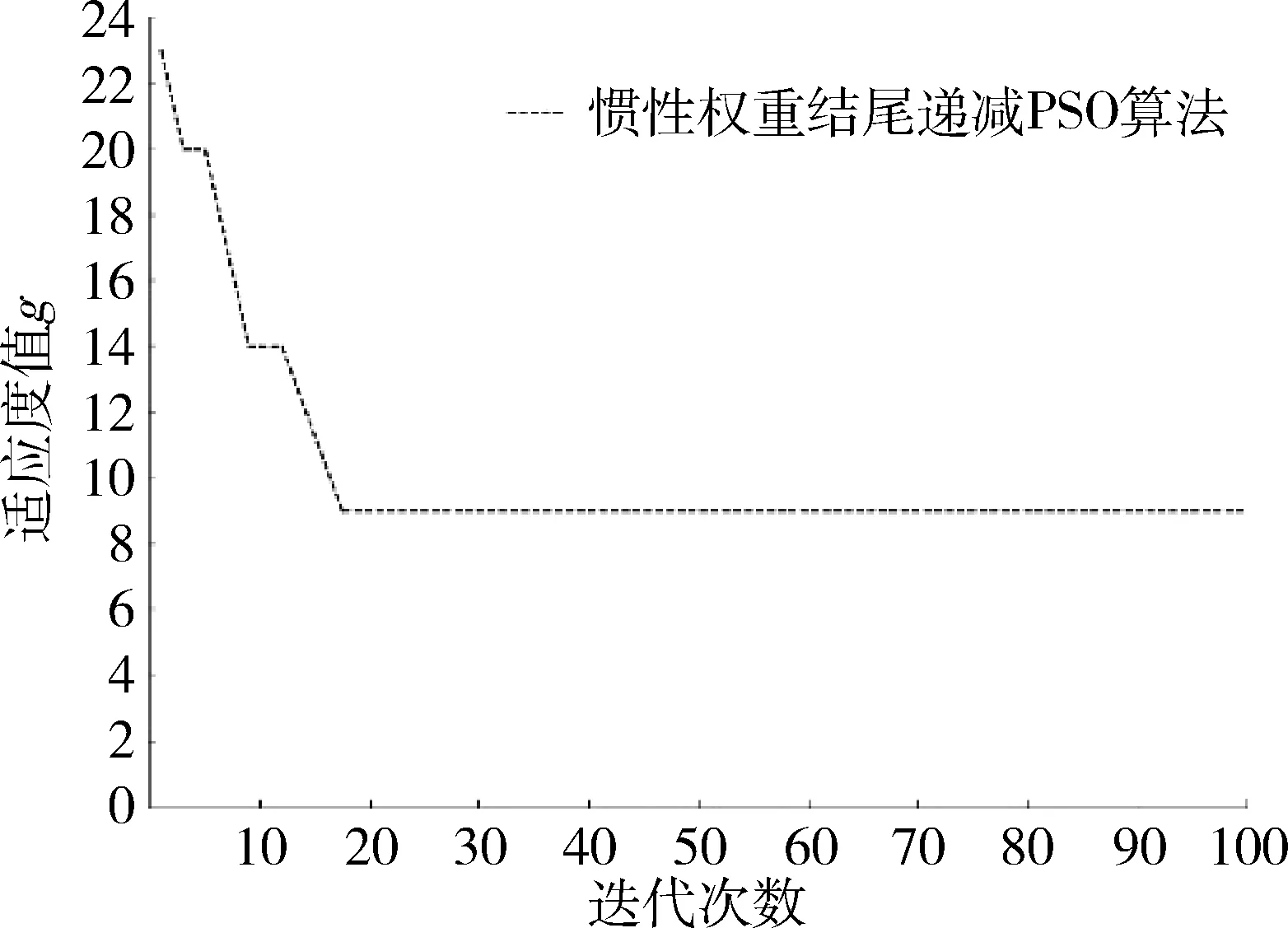
图2 适应度值曲线Fig.2 Fitness curve

最终在使用可用度A为0.86，保障费用C为19 827元时得最优解备件总数为9件，各部件初始备件个数如表2所示。

表1 备件参数表Table 1 Parameters of spare parts

表2 各部件的初始备件数量(件)Table 2 Number of initial spare parts

5 结束语

本文在考虑使用可用度最大和保障费用最小情况下，建立一种新的使用可用度与维修保障费用的计算模型，以装备k/N系统不同保障备件初始备件数为目标函数，利用改进的粒子群算法，对初始备件配置进行优化，得到最优的备件配置方案。在具备必要的备件参数情况下，文中提出的使用可用度模型和维修费用模型可以广泛应用至更为庞大的k/N系统，为保障人员提供备件保障决策，提高系统备件保障的经济性，对部队备件配置有着极其重要的作用。

[1] 刘刚,钟小军,董鹏.基于遗传算法和神经网络的舰船电子装备备件优化模型研究[J].舰船科学技术,2008,30(5):138-142.

LIU Gang，ZHONG Xiao-jun，DONG Peng.Research on Warship Electronic Equipment’s Spare Parts Optimize Model Based on Genetic Algorithm and Neural Network[J].Ship Science and Technology，2008，30(5)：138-142.

[2] 郑小丽,黎放,狄鹏.整数规划PSO算法在备件优化配置中的应用研究[J].舰船电子工程,2009,29(3):133-135.

ZHENG Xiao-li，LI Fang，DI Peng.Research on Application of Integral Programming PSO Algorithm to Spare Part Optimizing[J].Ship Electronic Engineering，2009,29(3):133-135.

[3] 宋贵宝,马广婷,刘学君,等.基于粒子群算法的导弹初始备件优化配置[J].舰船电子工程，2012,32(9)：118-120.

SONG Gui-bao，MA Guang-ting，LIU Xue-jun，et al.Optimal Allocation of Initial Spares of Missile Based on Particle Swarm Optimization Algorithm[J].Ship Electronic Engineering，2012,32(9)：118-120.

[4] 倪现存,左洪福,刘明,等.基于免疫粒子群算法的民机备件库存配置优化方法研究[J].机械科学与技术，2008(12):1660-1664.

NI Xian-cun，ZUO Hong-fu，LIU Ming，et al.A Method for Civil Aircraft Spare Parts Inventory Allocation Based on Particle Swarm Optimization with Immunity Algorithms[J].Mechanical Science and Technology for Aerospace Engineering，2008(12):1660-1664.

[5] Francesco Costantino，Giulio Di Gravio，Massimo Tronci.Multi-Echelon，Multi-Indenture Spare Parts Inventory Control Subject to System Availability and Budget Constraints[J].Reliability Engineering and System Safety，2013,119:95-101.

[6] 王亚彬,赵建民,程中华,等.基于改进MOPSO的多级系统备件配置优化研究[J].系统工程与电子技术，2015,37(7)：1581-1586.

WANG Ya-bin，ZHAO Jian-min，CHENG Zhong-hua，et al.Optimization for Spare Parts Allocation in Multi-Echelon Support System Based on Improve MOPSO[J].Systems Engineering and Electronics，2015,37(7):1581-1586.

[7] 阮旻智,李庆民,李承,等.改进的分层边际算法优化备件的初始配置方案[J].兵工学报，2012,33(10)：1251-1257.

RUAN Min-zhi，LI Qing-min，LI Cheng，et al.Improved-Layered-Marginal Algorithm to Optimize Initial Spare Part Configuration Project[J].Acta Armamentarii，2012,33(10)：1251-1257.

[8] 金星,洪延姬,张明亮,等.不同单元构成的任意k/N系统可靠度近似评定方法[J].弹箭与制导学报,2004,24(3):74-76.

JIN Xing，HONG Yan-ji，ZHANG Ming-liang，et al.Approximate Reliability Evaluation Method ofk-out-of-NSystem Consisted of Different Units[J].Journal of Projectiles，Rockets，Missiles and Guidance,2004，24(3):74-76.

[9] 艾宝利,武昌.两级维修保障下k/N系统使用可用度模型[J].系统工程学报,2011,26(3):421-426.

AI Bao-li，WU Chang.Operational Availability Model fork/NSystem Under Two Grade Maintenance Support Policy[J].Journal of Systems Engineering，2011,26(3)：421-426.

[10] 方永锋,陈建军,曹鸿钧.可修复的k/N表决系统的可靠性分析[J].西安电子科技大学学报,2014,41(5):180-184.

FANG Yong-feng，CHEN Jian-jun，CAO Hong-jun.Analysis of Dynamic Reliability of the Repairablek-out-of-NSystem under Several Times Shocks[J].Journal of Xidian University，2014,41(5)：180-184.

[11] 张永强,徐宗昌,呼凯凯,等.k/N系统维修时机与备件携行量联合优化[J].北京航空航天大学学报,2016,42(10):2189-2197.

ZHANG Yong-qiang，XU Zong-chang，HU Kai-kai，et al.Joint Optimization of Maintenance Time and Carrying Spare Parts fork-out-of-NSystem[J].Journal of Beijing University of Aeronautics and Astronautics，2016,42(10)：2189-2197.

[12] ERIK T S B,HARAREH T，DRAGAN B.Joint Optimal Inspection and Inventory for ak-out-of-NSystem[J].Reliability Engineering and System Safety，2014,131：203-215.

[13] 刘福胜.装甲装备使用可用度研究[D].北京：装甲兵工程学院，2010:63-64.

LIU Fu-sheng.Research on Operational Availability of Armored Equipment[D].Beijing：Academy of Armored Force Engineering，2010:63-64.

[14] 丁定浩，陆军.装备寿命周期使用保障的理论模型和设计技术[M].北京：电子工业出版社，2011.

DING Ding-hao，LU Jun.The Theoretical Model and Design Technology of Equipment Life Cycle Guarantee[M].Beijing：Publishing House of Electronics Industry，2011.

[15] 刘开丽.粒子群优化算法的研究与应用[D].合肥：安徽大学,2013:20-21.

LIU Kai-li.Research and Application of Particle Swarm Optimization Algorithm[D].Hefei：Anhui University，2013:20-21.

OptimizationModelforSparePartsAllocationinEquipmentk/NSystem

FU Bing，LIU Fu-sheng，YAN Xu

(Academy of Armored Force Engineering，Department of Technical Support Engineering，Beijing 100072，China)

Spare parts are important parts of equipment support resources, and they play key roles to ensure that equipment system can be in a good state of combat readiness to recover effectiveness. In view of the problem that unreasonable allocation of spare parts ink/Nsystem leads to the low support benefit in preventive maintenance, we propose a new optimization model spare parts allocation. In the model, considering the impact of different failure types on the configuration of the spare parts，we regard the original number of spare parts allocation as the objective function and the availability and maintenance support costs as constraints. The settlement efficiency can be increased by using particle swarm optimization algorithm which is improved by the strategy of decreasing inertia weight to make a reasonable optimal allocation for spare parts. At last，an example is given and the result shows that the model can be reasonable to allocate the spare parts and find the optimal allocation program of spare parts to improve the effectiveness of equipment system security.

k/Nsystem；spare parts；operational availability；support cost；allocation optimizing；improved particle swarm optimization

2017-03-16；

2017-05-04

付冰(1993-)，男，陕西渭南人。硕士生，主要研究方向为装备综合保障。

通信地址：100072 北京丰台区杜家坎21号院E-mail：losser06@163.com

10.3969/j.issn.1009-086x.2017.05.025

E917;N945.17

A

1009-086X(2017)-05-0155-07