临近空间平台系统效能评估及稳定性分析*
赵永龙,韩晓明,余丽山
(空军工程大学 防空反导学院,陕西 西安 710051)
临近空间平台系统效能评估及稳定性分析*
赵永龙,韩晓明,余丽山
(空军工程大学 防空反导学院,陕西 西安 710051)
从6个方面建立临近空间平台系统效能评估指标体系,构建灰色层次评估模型。针对数据获取不准确导致的评估结果不确定性,采用蒙特卡罗方法对评估结果开展稳定性分析。仿真结果表明,基于蒙特卡罗的评估与灰色层次评估结果一致,即采用灰色层次模型对临近空间平台系统效能评估结果是可信的,为临近空间平台系统效能评估提供一种合理方法。
低动态临近空间平台系统;灰色层次模型;蒙特卡罗;效能评估;稳定性分析;Beta分布
0 引言
随着信息技术和航空航天技术的迅猛发展,现代化作战样式不断更新,作战领域不断延伸,临近空间作为近年来研究的热点问题,成为未来作战重要领域[1]。临近空间平台是适应现代化作战需要,通过搭载不同的应用载荷,实现预警探测、电子对抗以及防空反导等多样化任务的远程作战平台[2]。目前,美军正在积极开发临近空间机动飞行器(near space maneuver vehicle,NSMV)与自由漂浮平台以用于军事通信领域[3],孙鹏等通过仿真计算验证了临近空间平台在防空反导领域的巨大应用价值[4]。但是,目前对临近空间平台系统效能仍然没有一个规范的指标体系和行之有效的评价方法。
临近空间平台按飞行速度可以分为高动态和低动态2类[5]。低动态临近空间平台具有信息感知范围大、留空时间长、生存能力强、任务载荷大、效费比高等显著优点[6]。采用灰色层次分析法进行效能评估时,由于专家打分过程中产生的不稳定,导致评估结果的可信性降低。本文采用蒙特卡罗方法对建立的灰色层次模型进行评估过程稳定性分析,通过稳定性分析结果进一步验证灰色层次模型的可用性,较好地完成了低动态平台系统效能的评估,可以为临近空间发展提供参考。
1 指标体系构建及权重确定
1.1指标体系
按照指标体系选取的原则,以系统需求为基础,对系统功能特征进行归纳,结合应用需求和使用目标,系统归纳了6个一级指标以及支撑一级指标的多项底层指标,如图1所示。
1.2权重确定
为了解决传统层次分析法确定权重过程中标准难以把握及一致性检验的困难,文中引入三标度法则和最优传递矩阵来确定权重[7]。
(1) 确定判断矩阵
根据构建的指标体系,运用-1,0,1的三标度法则构造判断矩阵,法则如表1所示。

表1 三标度比例法则Table 1 Three scaling law
备注:aij表示元素i比元素j的重要性程度
(2) 最优传递矩阵R和拟传递矩阵H
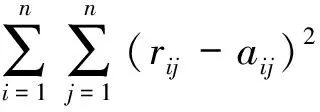
(1)
存在矩阵H=eR,称矩阵H为矩阵A的一个拟优化传递矩阵,且满足hij=erij。H本身是一致性矩阵,无需进行一致性检验。
(3) 权重值的计算
已知拟传递矩阵H,即可求得权重值Wi,有
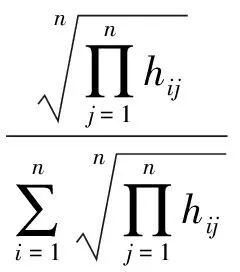
(2)
2 基于灰色层次分析的效能评估
2.1评估对象的选择
美军“全球鹰”作为美国空军最先进的高空长航时无人机,是现役少数能进入临近空间的低动态平台系统的典型代表,已经发展出RQ-4A,RQ-4B和“欧洲鹰”等类型,RQ-4B是美国最新的高空长航时无人机情报侦察平台,由于优异的性能受到了美国、日本、韩国和欧盟等国家和地区的青睐。结合美军对其现已公开的性能参数及战术技术指标,以RQ-4B为研究对象对平台系统效能评估展开研究[8-11]。

图1 低动态临近空间平台系统效能指标体系Fig.1 Performance index system of low dynamic near space platform
2.2指标权重计算
根据建立的指标体系,逐级确立指标权重。以第1层指标为例,权重计算如表2所示。
同理,可获得第2层指标的权重值。
2.3效能值的计算
(1) 制定评分等级
组织临近空间领域相关专家共10名,将指标按照优劣等级划分为优秀、良好、一般、差4个等级,其对应的值可分别赋予4,3,2,1,当指标介于两者之间时,相应评分为3.5,2.5,1.5,表3是专家对B方案各指标的评分表。
(2) 确定评价灰类
本文设定4个灰类,灰类序号为e=1,2,3,4。分别表示“优”、“良”、“中”、“差”,根据专家评价矩阵中最大、最小和中间评价数据作为灰类计算的阈值,可以得到所划分的灰类及灰类对应的白化权函数如表4所示。
(3) 综合评估
先计算二级指标属于各评价灰类的灰色评价系数。
抗氧化性指标属于4个评价灰类的灰色评价系数分别为
x111=8.625;x112=8.333;x113=2.75;x114=0.
相应的灰色权向量为
r11=(0.437 6,0.422 8,0.139 6,0).
对系统综合效能进行评价计算,得出灰色综合评价向量为
B1=A1·RB=(0.416 9,0.408 5,0.143 8,0),

表2 一级指标权重Table 2 First level index weight
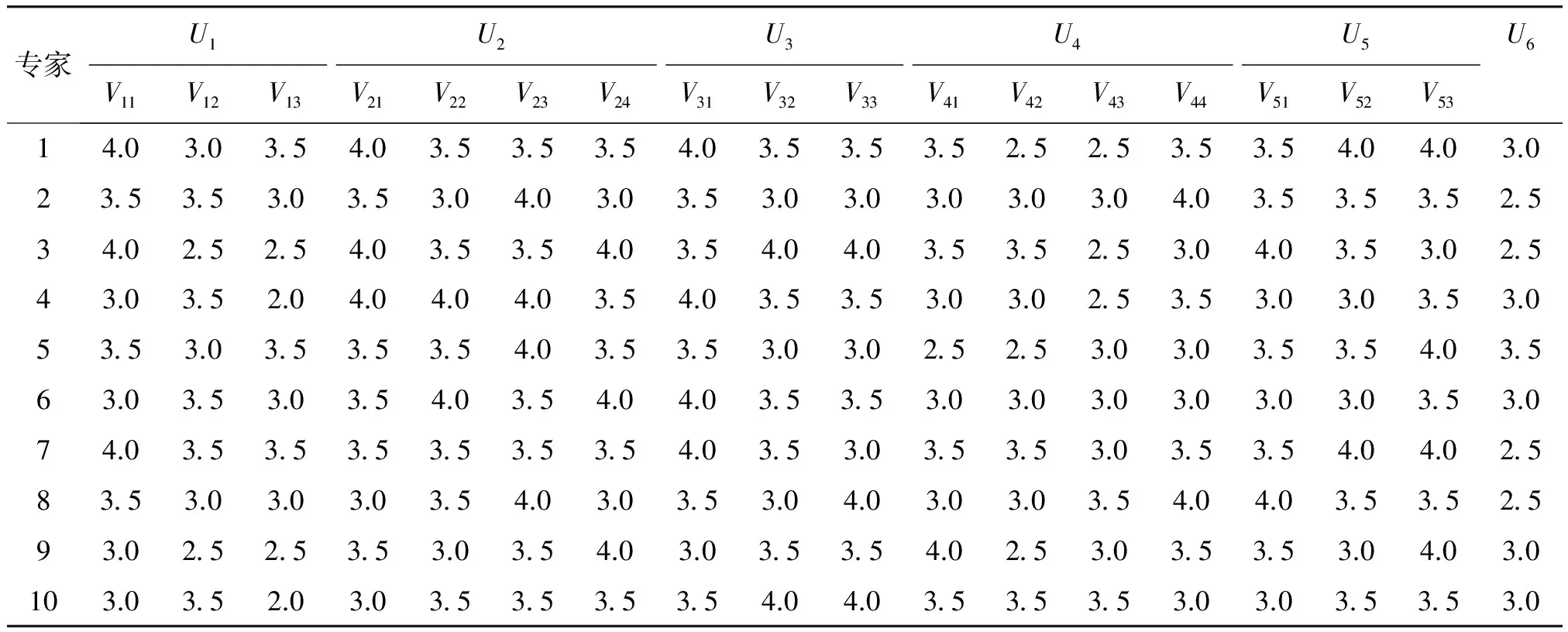
表3 RQ-4B专家评分表Table 3 Expert score sheet of RQ-4B
式中:A1为一级指标权重系数向量,得出综合评价向量中各数分别为平台系统综合效能属于各灰类等级的综合评价值,其值越大,表示系统效能属于对应灰等级的可能性越大。由评价结果得出其属于第1类“优”的综合评分值0.416 9和属于第2类“好”的评分值0.408 5都远大于系统效能属于第3类“中”的评分值,系统属于第1类的效能值最大,表明该型号综合评价为“优”,且性能已经超出第2类“好”和第3类“中”的水平。
将各灰类等级按“灰水平”赋值,4种评价等级按“灰水平”赋值的等级值化向量为C=(4,3,2,1),则系统值化综合评价值为
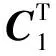
(4,3,2,1)T=3.180 9。
按照同样的步骤和方法对RQ-4A平台系统进行综合评价,得出其综合效能评估值为
W2=B2·CT=(0.364 5,0.410 0,0.192 3,0)·
(4,3,2,1)T=3.180 9。
通过计算可得:RQ-4A平台系统属于第1类“优”的评分值0.334 5,而PQ-4B属于第1类“优”的评分值为0.416 9。比较其综合评判值,2种平台系统的综合效能值W1>W2,表示RQ-4B的综合评估值大于RQ-4A,其结果也较好地反映了RQ-4B是在RQ-4A平台系统的基础上改进而来的实际情况,因而其综合效能较高。
3 基于蒙特卡罗(MCL)的评估稳定性分析
使用灰色层次分析法进行评估时,指标评估数据基本由专家评估所得,评估过程中专家对低动态临近空间平台系统和性能的认识会存在一定的差异和偏差,在评估信息上往往会存在一定的不确定性[12-13],故需要对评估过程进行稳定性分析。
蒙特卡罗方法的基本思路是,当所求解问题是某种随机事件出现的概率,或者是某个随机变量的期望值时,通过某种“实验”的方法,以这种时间出现的频率来估计该随机时间的概率,或者得出这个随机变量的某种数字特征,并将其作为问题的解[14-15]。
3.1仿真数据的获取
仿真数据源是武器系统效能评估需要的重要数据来源之一。本文考虑的评估结果的不确定性主要体现在现在评估数据源的波动对评估结构的影响。因此,需要对评估数据源进行统计分析,在评估数据源的概率密度上抽样分析数据源的波动对评估稳定性的影响[16]。
设F(x)是某随机变量的分布函数,α和β是给定的正实数,则称随机变量X服从广义的Beta分布, 在实际应用中,Beta分布通常采用其共轭分布—β(R|a,b)分布,其密度函数为
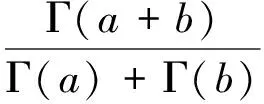
(3)
式中:0

表4 白化权函数Table 4 Whitening weight function
根据所取参数的不同,Beta分布具有多种不同的分布形式,通过改变形状参数α,β就可以逼近多种分布形式。因此,在数据处理中如果采用Beta分布,就可以通过实际情况拟合参数,利用Beta分布表示其误差分布,从而可以更加精确的拟合评估数据源[15]。图2是当α=1,β从0.25~3之间取值时Beta分布的图像。

图2 Beta分布函数曲线Fig.2 Function curve of Beta distribution
3.2稳定性分析
根据建立的指标体系和平台系统专家打分方法,对低动态临近空间平台系统效能进行稳定性分析。采用10个专家进行评判,分别得到各专家对各方案的效能评估指标值,评价指标中二级指标的排列序号从左到右分别为1~18。假设“专家”群对指标的评价值规范化处理后服从Beta分布。由MAatlan的Betafit[R,alpha]命令就计算出Beta分布参数α和β,其中R是数据样本,alpha是控制置信区间的宽度参数。由于Beta分布函数的定义域为[0,1],通过10个专家对指标的打分值确定各指标在Beta分布函数上的随机取值的数据区间,可以分别得到2个方案各指标参数随机取值区间如表5,6所示。
由于性能指标数据的不完全,组织的专家只能通过自身经验和认识对各效能指标进行评定打分。由于RQ-4B是在RQ-4A上的改进型,所以对于部分未公开的性能参数和对比变化不明显的指标参数的打分采用相同的打分值。由于Beta分布的定义域在[0,1]范围之内,本文对专家打分先进行规范化预处理,然后根据各指标参数服从的Beta分布函数性质,可以分别做出2种平台系统方案的指标评分所得的拟合曲线,其中横坐标表示专家评分的可能值,纵坐标表示仿真数据在数据源中出现的次数。实线表示RQ-4B指标分布曲线,虚线表示RQ-4A指标分布曲线,得到它们的典型分布函数曲线有以下3种,如图3所示。
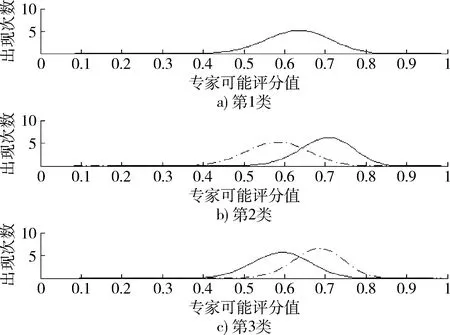
图3 典型分布函数曲线Fig.3 Typical distribution function curve

表5 RQ-4B指标参数和取值区间Table 5 Index parameter and value interval of RQ-4B
第1类曲线表示方案指标性能参数相同或参数信息不完整导致的专家评分数据相同时的指标分布曲线,在本评估实例中包括抗氧化性、耐腐蚀性、耐热性、悬停能力、抗杀伤能力、自动修复能力、可用性、安全性以及可靠性、维修性与保障性指标,同时包括一级指标中环境适应性和可信性2个指标;第2类曲线表示RQ-4B指标评分值优于RQ-4A,主要包括飞行范围、机动性与部署能力、连续工作时间、承载能力、稳定与遥测能力、能源供应能力和敏感性等二级指标;第3类曲线表示RQ-4B指标评分值低于RQ-4A,包括突防能力和经济性2个指标。
通过仿真数据的分析,各评估指标分布函数和相关权重向量都已经得出,这些分量与各指标的权重进行加权得到整个方案的综合能力,由于专家对一级指标中环境适应性和可信性2个指标的评分值差异不大,对综合效能的影响不大,对其余一级指标进行加权求和后得到服从Beta分布的效能函数曲线如图4所示。
图4中横坐标表示规范化以后的效能值。从图4可以看出,2个方案在环境适应性、生存性能和可信性3个一级指标效能评价值相差不大,而平台性能、飞行性能和综合性能RQ-4B评价值明显大于RQ-4A。本文根据仿真数据源拟合的Beta分布横坐标表示可能取得的指标评价值,纵坐标表示在仿真次数内给指标值出现的最优可能次数,分析两者综合效能值,从仿真曲线的来看,专家对综合效能值的仿真结果分别集中于[0.6,0.8]和[0.5,0.7]上,这表明专家对仿真结果的认识比较集中,专家评估数据生成的分布函数上抽样的值与评估数据差异较小。同时RQ-4B综合效能曲线在[0.70,0.75]范围内取得最大值,相应RQ-4A效能曲线在[0.60,0.65]上取得最大值,表明RQ-4B综合效能取值在[0.70,0.75]范围内的次数明显较多,即最有可能取得该范围内的评价值,明显高于RQ-4A的最优可能的仿真效能值。从综合效能的分布曲线来看,方案RQ-4B得到最大综合效能值的次数最多时,其效能指标值明显大于方案RQ-4A,且从分布函数下方面积上看,方案RQ-4B在区间[0.6,0.9]上的次数显然高于方案RQ-4A在相同区间上的次数,综合表明B方案的综合效能值高于方案A的概率较大。

图4 一级指标分布曲线对比图Fig.4 Comparison of the first grade index distribution curve

表6 RQ-4A指标参数和取值区间Table 6 Index parameter and value interval of RQ-4A
下面分别从得到的概率密度函数上进行抽样,蒙特卡罗的循环条件设置为1 000。通过仿真流程的实现得到计算结果如表7所示。
从蒙特卡罗方法计算的结果来看,RQ-4B成为最优方案的次数远远大于RQ-4A,在总仿真次数中所占的比例明显较高。将排名的次数乘以排名再求和,所得到的值除以1 000得到各方案排名的期望值,对于RQ-4B有
(964×1+36×2)/1 000=1.038.
同理得到方案RQ-4A的期望排名为1.964。从稳定性分析的结果中不难得出,RQ-4B成为最优方案的可能性为96.4%,相应RQ-4A成为最优方案的可能性仅为3.6%。灰色层次综合评估的结果为:方案RQ-4B的综合效能值大于方案RQ-4A,通过稳定性分析可以得出,专家对于2种方案效能的综合评估值基本符合现实,且根据专家评估数据生成的分布函数上抽样的值与原始评估数据差异较小,由专家评估数据的灰色不确定性对评估流程的影响较小。

表7 稳定性分析结果Table 7 Result of stability analysis
4 结束语
通过使用蒙特卡罗仿真的方法,利用Beta分布函数的性质,对现有的低动态临近空间典型平台系统的综合效能评估过程进行稳定性分析。其中设计方案RQ-4B为最优方案,对评估结果做稳定性分析得出方案成为最优方案的可能性最大,为96.4%,其期望排名为1.038,方案RQ-4A的期望排名为1.964。结果完全符合该装备发展的现状,实验证明整个评估过程合理、有效。
[1] 梁晓庚,田宏亮.临近空间高超声速飞行器发展现状及其防御问题分析[J].航空兵器,2016(4):3-10.
LIANG Xiao-geng,TIAN Hong-liang.Analysis of the Development Status and the Defense Problem of Near Space Hypersonic Vehicle[J].Aero Weaponry,2016(4):3-10.
[2] 薛永江,李体方.改进灰色层次效能法在临近空间平台效能评估中的应用研究[J].航天制造技术,2010(6):40-43.
XUE Yong-jiang,LI Ti-fang.Application Research on Improved Grey Hierarchy Method in Efficiency Evaluation of Near Space Aircraft[J].Aerospace Manufacturing Technology,2010(6):40-43.
[3] 兰俊杰.美军临近空间通信支援系统发展及启示[J].飞航导弹,2014(12):49-51.
LAN Jun-jie.The Development and Enlightenment of US Military Space Communication Support System[J].Aerodynamic Missile Journal,2014(12):49-51.
[4] 孙鹏,杨建军.临近空间平台防空反导作战运用仿真研究[J].弹箭与制导学报,2011,31(2):14-16.
SUN Peng,YANG Jian-jun.The Study on Proximity Space Platform in Air Defense and Antimissile Operation Based on Simulation[J].Journal of Projectiles,Rockets,Missile and Guidance,2011,31(2):14-16.
[5] 南海阳,韩晓明,刘洪引,等.国外临近空间飞行器发展现状及趋势[J].飞航导弹,2014(10):3-8.
NAN Hai-yang,HAN Xiao-ming,LIU Hong-yin,et al.Development Status and Trend of Foreign Near Space Vehicles[J].Aerodynamic Missile Journal,2011(10):3-8.
[6] 安合志,李萍,王蕾蕾.临近空间平台作战效能影响研究[J].电子科技,2012,25(9):13-15.
AN He-zhi,LI Ping,WANG Lei-lei.Operational Performances of the Near-Space Platform[J].Electronic Science and Technology,2012,25(9):13-15.
[7] 常健,张志军,王君莉.三标度模糊层次分析法在桥梁安全评估中的应用[J].中国安全生产科学技术,2014,10(8):156-161.
CHANG Jian,ZHANG Zhi-jun,WANG Jun-li.Application of Three-Scale Fuzzy Analytic Hierarchy Process in Bridge Safety Assessment[J].Journal of Safety and Technology,2014,10(8):156-161.
[8] 沉舟,福子.RQ-4全球鹰无人机验证扩展任务能力[J].飞航导弹,2014(10):1.
CHEN Zhou,FU Zi.RQ-4 Global Hawk Unmanned Aerial Vehicle to Verify Extended Mission Capability[J].Aerodynamic Missile Journal,2014(10):1.
[9] 季华益.“全球鹰”及其对抗策略思考[J].航天电子对抗,2013,29(1):26-30.
JI Hua-yi.Global Hawk and Thinking of Countermeasures Against It[J].Aerospace Electronic Warfare,2013,29(1):26-30.
[10] 陈晶,许军,吴微露.全球鹰无人机的升级及试验情况[J].飞航导弹,2015(5):15-17.
CHEN Jing,XU Jun,WU Wei-lu.The Introduction of Global Hawk UAV Upgrade and Test[J].Aerodynamic Missile Journal,2015(5):15-17.
[11] 林岳铮,祝利,王海.全球鹰无人侦察机的技术特点与应用趋势[J].飞航导弹,2011(9):21-24.
LIN Yue-zheng,ZHU Li,WANG Hai.Technical Characteristics and Application Trend of Global Hawk UAV[J].Aerodynamic Missile Journal,2011(9):21-24.
[12] 杨峰,王唯平.武器装备作战效能仿真与评估[M].北京:电子工业出版社,2010.
YANG Feng,WANG Wei-ping.Weapons and Equipment Operational Effectiveness Simulation and Evaluation[M].Beijing:Publishing House of Electronics Industry,2010.
[13] 刘东亮,徐浩军,闵桂龙.航空人-机复杂系统极值风险评估稳定性分析[J].系统工程与电子技术,2012,34(12):2504-2508.
LIU Dong-liang,XU Hao-jun,MIN Gui-long.Stability Analysis of Aeronautic Man-Machine Complex System Risk Evaluation by Extremum Theory[J].Systems Engineering and Electronics,2012,34(12):2504-2508.
[14] 刘东亮,徐浩军,蔡军,等.基于Monte Carlo仿真的小概率事件评估算法稳定性研究[J].数学的实践与认识,2012,42(10):68-73.
LIU Dong-liang,XU Hao-jun,CAI Jun,et al.Arithmetic Stability Analysis of Extreme Risk Evaluation Based on Monte Carlo Simulation Method[J].Mathematics in Practice and Theory,2012,42(10):68-73.
[15] 夏焕雄,向东,牟鹏.宏观自洽的Monte Carlo方法及应用[J].清华大学学报:自然科学版,2013,53(10):1434-1440.
XIA Huan-xiong,XIANG Dong,MOU Peng.Macro-State Self-Consistent Monte Carlo Method[J].Journal of Tsinghua University:Natural Science ed,2013,53(10):1434-1440.
[16] 许国珍,焦鹏,查亚兵.基于元数据的仿真数据质量研究[J].系统仿真技术,2012,8(2):133-137.
XU Guo-zhen,JIAO Peng,ZHA Ya-bing.Research of Simulation Data Quality Based on Metadata[J].System Simulation Technology,2012,8(2):133-137.
EffectivenessEvaluationandStabilityAnalysisfortheDynamicNearSpacePlatformSystem
ZHAO Yong-long,HAN Xiao-ming,YU Li-shan
(AFEU,Air and Missile Defense College,Shaanxi Xi′an 710051,China)
The performance evaluation index system of dynamic near space platform system is established from six aspects,and then the grey hierarchy evaluation model is constructed.Aiming at the uncertainty of the evaluation results due to fuzzy data,the Monte Carlo(MCL) method is used to analyze the stability of the evaluation results.The simulation results show that evaluation results based on MCL and grey hierarchy model are almost same,so the evaluation results from grey hierarchy model for dynamic near space platform system are credible,one kind of method is provided for near space platform system effectiveness evaluation.
dynamic near space platform system;grey hierarchy model;Monte Carlo;effectiveness evaluation; stability analysis;Beta distribution
2017-01-06;
2017-03-04
赵永龙(1991-),男,四川绵阳人。硕士生,主要研究方向为装备管理理论与方法。
通信地址:710051 陕西省西安市灞桥区长乐东路甲字一号空军工程大学防空反导学院研三队E-mail:13227876206@163.com.
10.3969/j.issn.1009-086x.2017.05.004
TJ861;N945.16
A
1009-086X(2017)-05-0017-07

