用于战术导弹气动参数辨识的输入设计研究*
杨闯,张弫
(北京电子工程总体研究所,北京 100854)
用于战术导弹气动参数辨识的输入设计研究*
杨闯,张弫
(北京电子工程总体研究所,北京 100854)
为了研究h=8 km,Ma=2条件附近导弹飞行试验中输入设计对气动参数辨识精度的影响,验证气动力模型的有效性,以方波信号为基础设计了3种开环舵偏指令。通过开环飞行弹道仿真试验,采用递推最小二乘法,对多项式非线性气动力模型中的气动参数进行了辨识。气动参数辨识结果表明,单级方波,偶极方波,“211”多级方波3种输入用于气动参数辨识是可行的,辨识精度是可接受的,辨识所用的纵向三自由度气动力模型是有效的。
战术导弹;气动参数辨识;输入设计;递推最小二乘;气动模型;飞行试验
0 引言
采用飞行试验数据进行气动参数辨识是验证导弹气动特性的一种有效方法。与固定翼飞机不同,对于战术导弹而言,其飞行试验成本较高,无法进行大批次的飞行试验,且每次飞行试验时间短暂,用于气动参数辨识的时间更是十分有限[1]。为了能在有限时间内充分激发导弹运动模态,使得飞行试验为导弹气动参数辨识提供所需信息量,提高气动参数辨识的精度,对辨识时间段内的输入信号进行精心设计是十分必要的[2-4]。
文献[5-7]的研究表明以方波信号为基础的输入设计对于有人驾驶飞机,闭环控制无人机,开环控制飞行器的气动参数辨识是有效的。战术导弹飞行试验中气动参数随着试验马赫数,高度,攻角等众多因素剧烈变化,为了提高气动参数辨识精度,在参考文献[8]中导弹纵向三自由度线性气动模型基础上,结合文献[9-13]中非线性气动力模型的构型,本文提出一种改进的纵向三自由度多项式形式非线性气动模型。
针对该气动力模型,在Ma=2,h=8 km的条件附近设计3种方波形式的输入指令,通过开环飞行弹道仿真试验获取试验数据,采取递推最小二乘法从仿真试验数据中辨识出相应气动参数,对3种输入的气动参数辨识效果进行分析研究,为飞行试验中用于气动参数辨识的输入设计提供一定的参考。
1 参数辨识最小二乘递推算法
战术导弹动力学系统参数辨识问题的一般性描述为[9]
(1)
式中:x(t)为n维状态向量;y(t)为m维输出向量;z(t)为m维观测向量;u(t)为l维输入向量;θ为p维参数向量;η(t)为q维随机噪声向量;Γ为n×q维系统噪声分布矩阵;F为已知实值函数;H为观测矩阵。
参数的递推估计,每取得一次新观测数据后,在前一次估计结果基础上,采用新引入观测数据对前次估计结果进行修正,从而递推得出新的参数估计值[14-15]。这样,随着新观测数据的不断引入,参数估计值不断更新,直到估计值达到满意的精度为止。其基本思想[15]可概括为
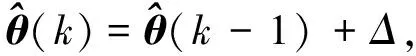
(2)

最小二乘参数估计的递推算法具体算式[15]如下:
(3)

(4)
式中:α为充分大的实数;ε为充分小的实向量。按上述算法进行递推计算,直到辨识参数向量满足以下收敛条件[15]:
(5)
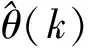
2 纵向气动参数辨识模型
早期飞行器外作用力模型一般采用线性模型,随着飞行器气动性能的不断提升,为了更精确描述外作用力,现代飞行器尤其是战术导弹一般多采用非线性气动力模型。
常用非线性模型包括多项式模型,样条函数模型,阶跃过渡函数模型等[9]。其中多项式模型是最简单方便的一种模型,由于其各项物理意义明确,模型有较高的光滑性,便于进行参数辨识,因此在工程实践中被广泛采用[9-10]。
2.1气动力及气动力矩模型
在对飞行器常用非线性气动力模型进行了分析研究后,本文针对战术导弹,提出了一种改进的纵向三自由度多项式形式的非线性气动力模型,具体表达式为[9-13]
(6)
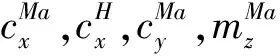
2.2状态方程组
在弹体坐标系中,导弹纵向三自由度状态方程组为
(7)
式中:vx,vy分别为导弹轴向速度和法向速度;ωz为导弹俯仰角速度;ϑ为导弹俯仰角;q为动压;S为参考面积;Jz为导弹俯仰转动惯量。
补充方程组:
(8)
式中:Nx,Ny分别为轴向过载和法向过载;ϑ为俯仰角;α为攻角;G为重力;R为发动机推力;φR,ψR为发动机推力偏心角。
2.3观测方程组
取导弹被动段俯仰角速度,轴向过载,法向过载,俯仰角,攻角作为气动参数辨识的观测量。观测方程组为
(9)
式中:vi(i=1,2,…,5)为互不相关的零均值高斯分布随机测量噪声。
2.4待辨识参数
待估计参数为式(6)气动模型中的未知参数,向量形式表达式为
(10)
3 仿真试验设计
方波式输入是导弹操纵机构一种典型的偏转方式,由于波形简单,工程上容易实现,且输入后导弹响应强烈,引起过渡过程中超调量较大,因此在用于气动参数辨识的飞行试验中被广泛采用[16-18]。
仿真试验共设计3条弹道,第1条弹道在t=30 s时断开稳定控制系统反馈回路,在辨识窗口内加载如图1a)所示的单极方波开环舵偏指令,图1b)为对应的攻角响应曲线。所加载的具体指令为
(11)
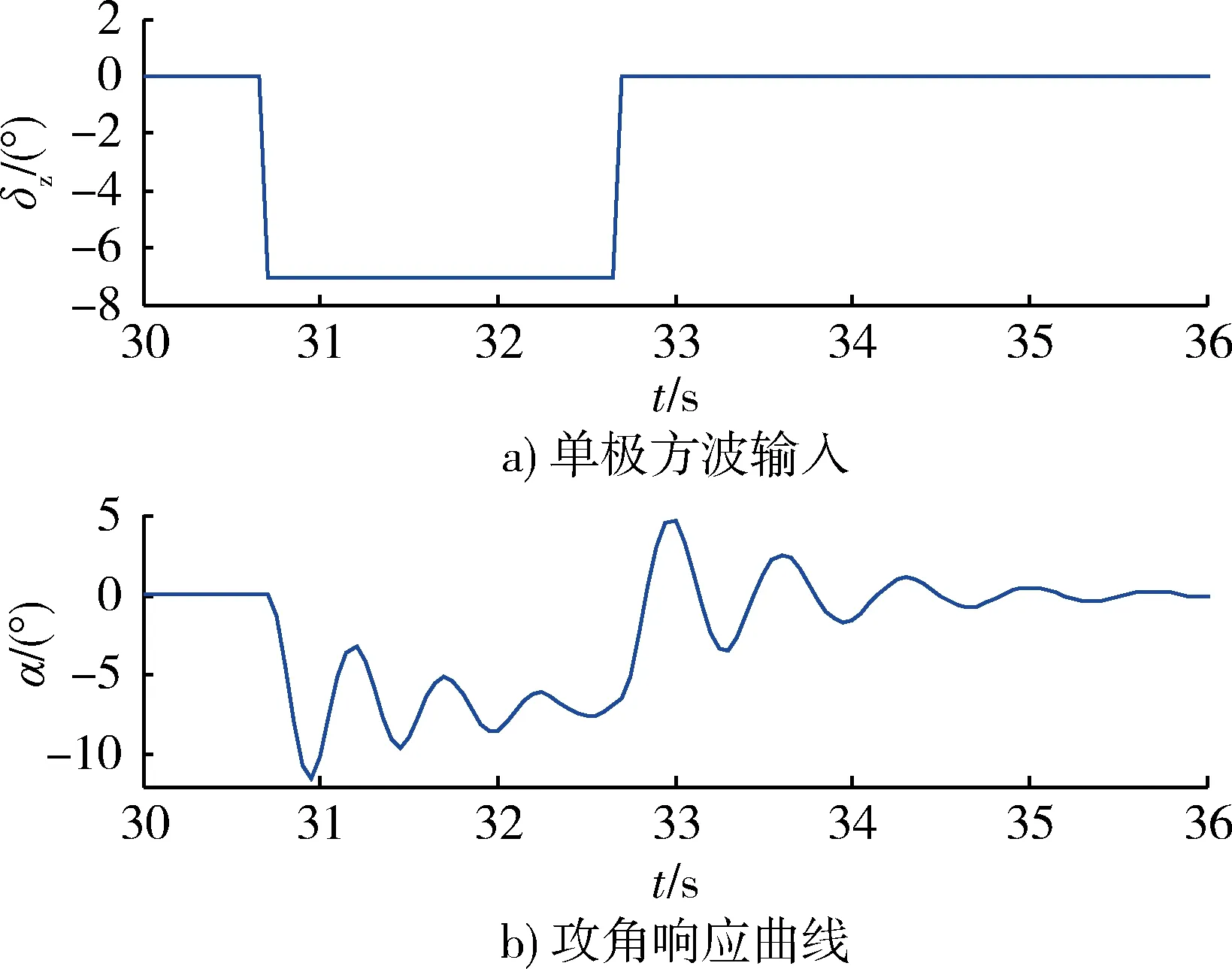
图1 单极方波输入及其攻角响应Fig.1 Single square wave input and the response of attack angle
第2条弹道在t=31 s时断开稳定控制系统反馈回路,在辨识窗口内加载如图2a)所示的偶极方波开环舵偏指令,攻角响应曲线如图2b)所示。加载具体指令为
(12)
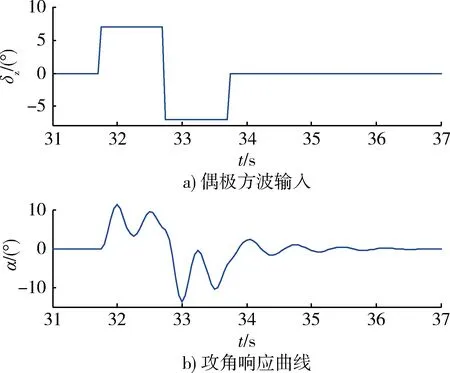
图2 偶极方波输入及其攻角响应Fig.2 Double square wave input and the response of attack angle
第3条弹道在t=31 s时断开稳定控制系统反馈回路,在辨识窗口内加载如图3a)所示的“211”多级方波开环舵偏指令,对应的攻角响应曲线如图3b)所示。具体指令为
(13)
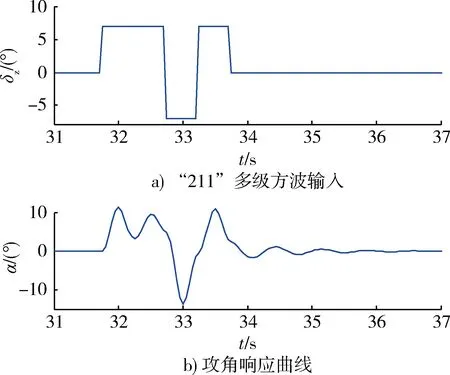
图3 “211”多级方波输入及其攻角响应Fig.3 “211” multistep square wave input and the response of attack angle
在仿真试验中,3条弹道理论上的辨识窗口为(8 km,2Ma)附近。由于加载的3种开环舵偏指令不同,在理论辨识窗口附近弹道会产生偏离,因此3条弹道实际的辨识窗口均取在(8±0.3 km,2±0.3Ma)的区间内,辨识窗口持续时间均为6 s,所加载的开环舵偏指令宽度均为2 s,幅值均为7°。图4给出了辨识窗口附近马赫数及高度的变化情况。表1为3条仿真弹道辨识窗口中马赫数与海拔高度的变化范围。

表1 辨识窗口对应马赫数与高度区间Table 1 Mach range and altitude range in identification window
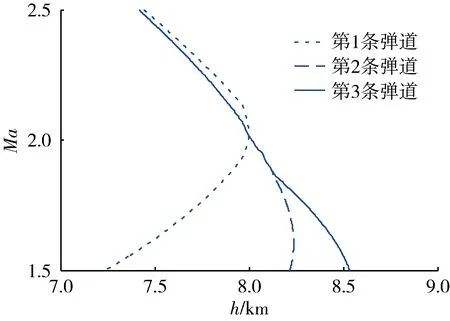
图4 辨识窗口附近马赫数及高度变化Fig.4 Variation of mach and altitude near identification window
4 辨识结果分析
根据弹道仿真试验数据,采用递推最小二乘法对导弹纵向各气动参数进行辨识,将各参数辨识结果汇总后分类进行比较分析。
4.1轴向力系数辨识结果
3种输入对轴向力系数辨识结果分别如图5~7所示。

图5 单极方波输入轴向力系数辨识结果Fig.5 Identification results of axial force coefficient using single square wave input
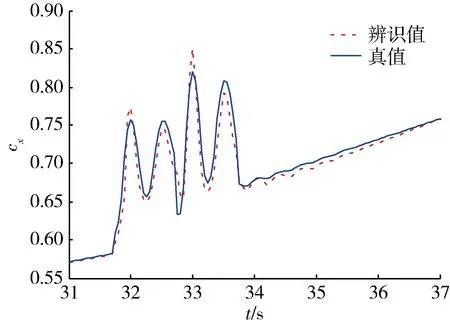
图6 偶极方波输入轴向力系数辨识结果Fig.6 Identification results of axial force coefficient using double square wave input
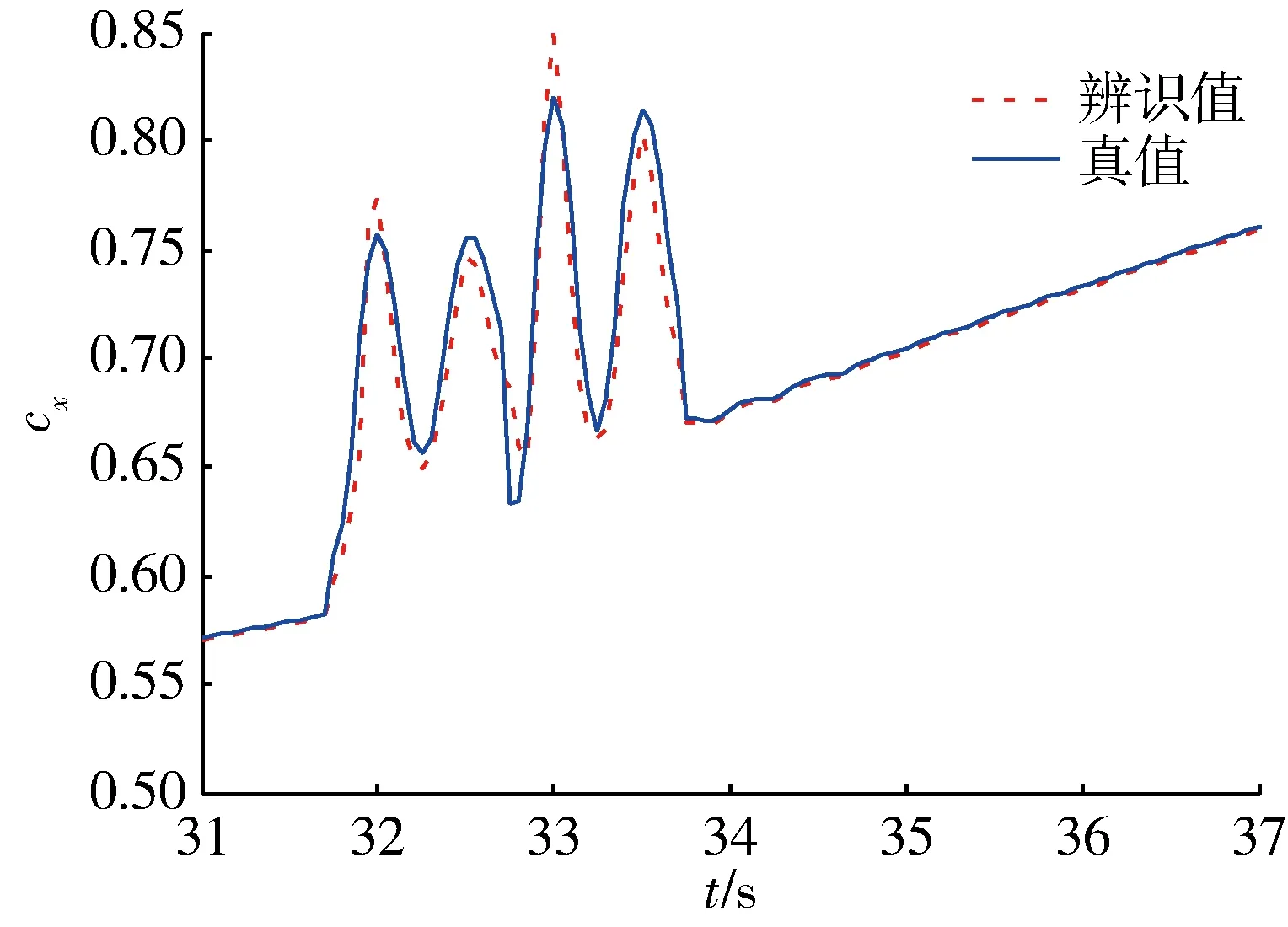
图7 “211”多级方波输入轴向力系数辨识结果Fig.7 Identification results of axial force coefficient using “211”multistep square wave input
3种输入对轴向力系数辨识精度的定量分析由表2给出。在辨识窗口内取120个辨识点计算其相对误差,经过统计后发现,对于轴向力系数,单极方波输入的辨识精度较高,平均相对误差为0.664%,偶极方波与“211”多级方波辨识相对误差次之。

表2 轴向力系数辨识相对误差Table 2 Relative error of axial force coefficient identification
4.2法向力系数辨识结果
图8~10分别为3种输入在辨识窗口内对法向力系数的辨识结果。
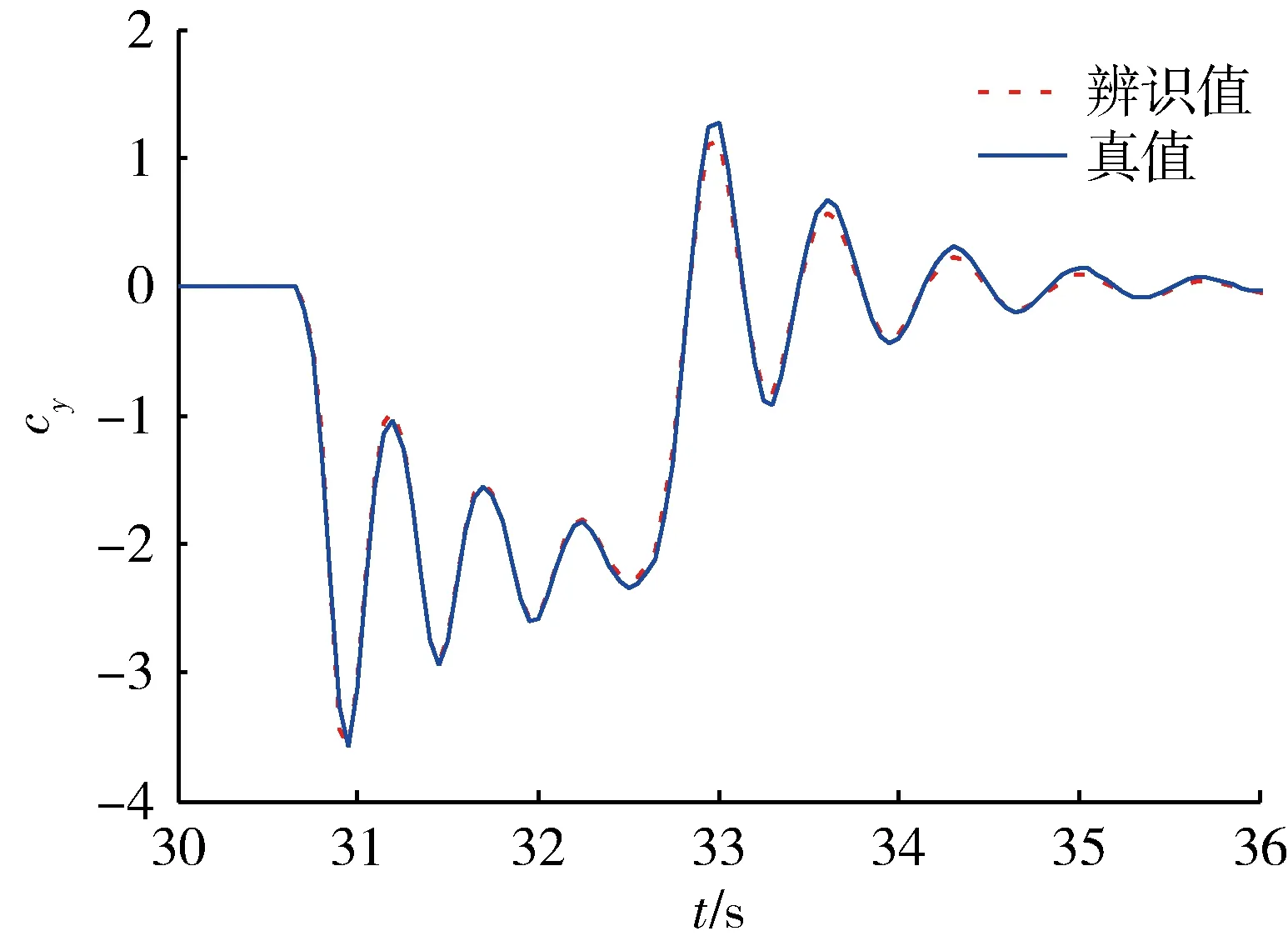
图8 单极方波输入法向力系数辨识结果Fig.8 Identification results of normal force coefficient using single square wave input

图9 偶极方波输入法向力系数辨识结果Fig.9 Identification results of normal force coefficient using double square wave input
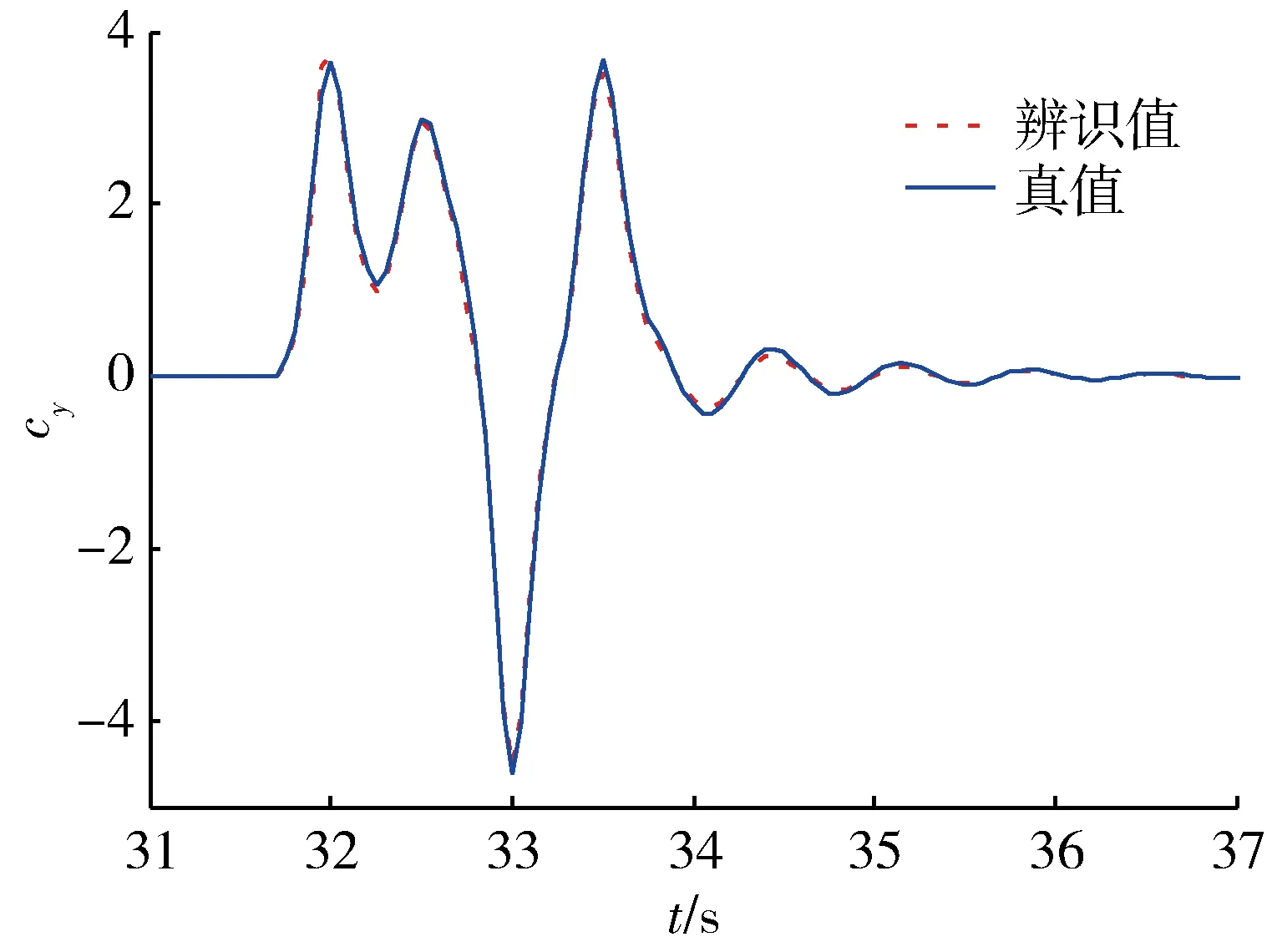
图10 ”211”方波输入法向力系数辨识结果Fig.10 Identification results of normal force coefficient using “211” multistep square wave input
表3为法向力系数辨识的相对误差。在辨识窗口内,对法向力系数辨识效果较好的是偶极方波输入,平均相对误差为5.774%,单极方波和“211”多级方波对法向力系数辨识的平均相对误差分别为6.110%和6.255%。

表3 法向力系数辨识相对误差Table 3 Relative error of normal force coefficient identification
4.3俯仰力矩系数辨识结果
图11~13分别为单极方波,偶极方波,“211”多级方波在辨识窗口内对俯仰力矩系数的辨识结果。

图11 单极方波俯仰力矩系数辨识结果Fig.11 Identification results of pitching moment coefficient using single square wave input
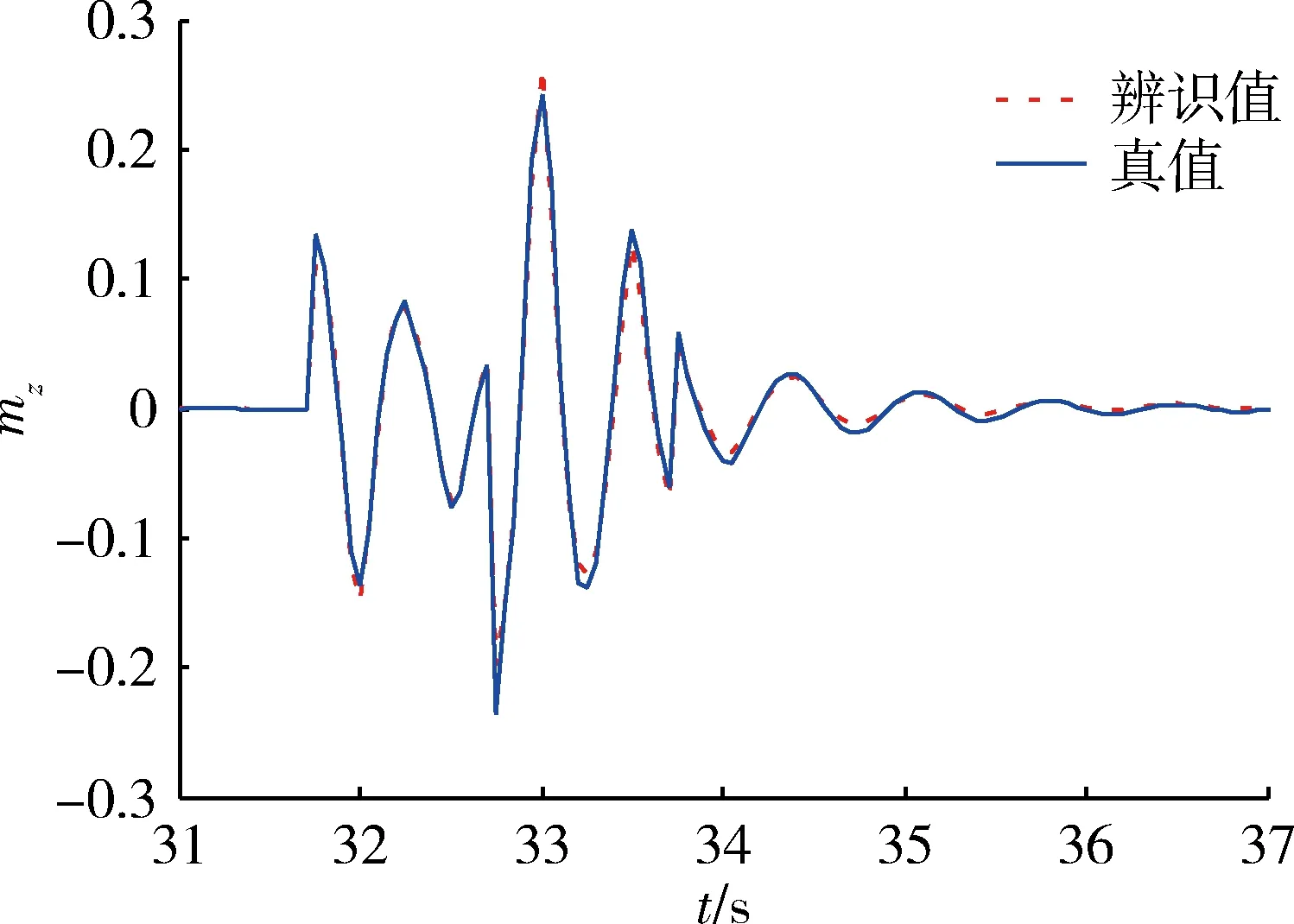
图12 偶极方波俯仰力矩系数辨识结果Fig.12 Identification results of pitching moment coefficient using double square wave input
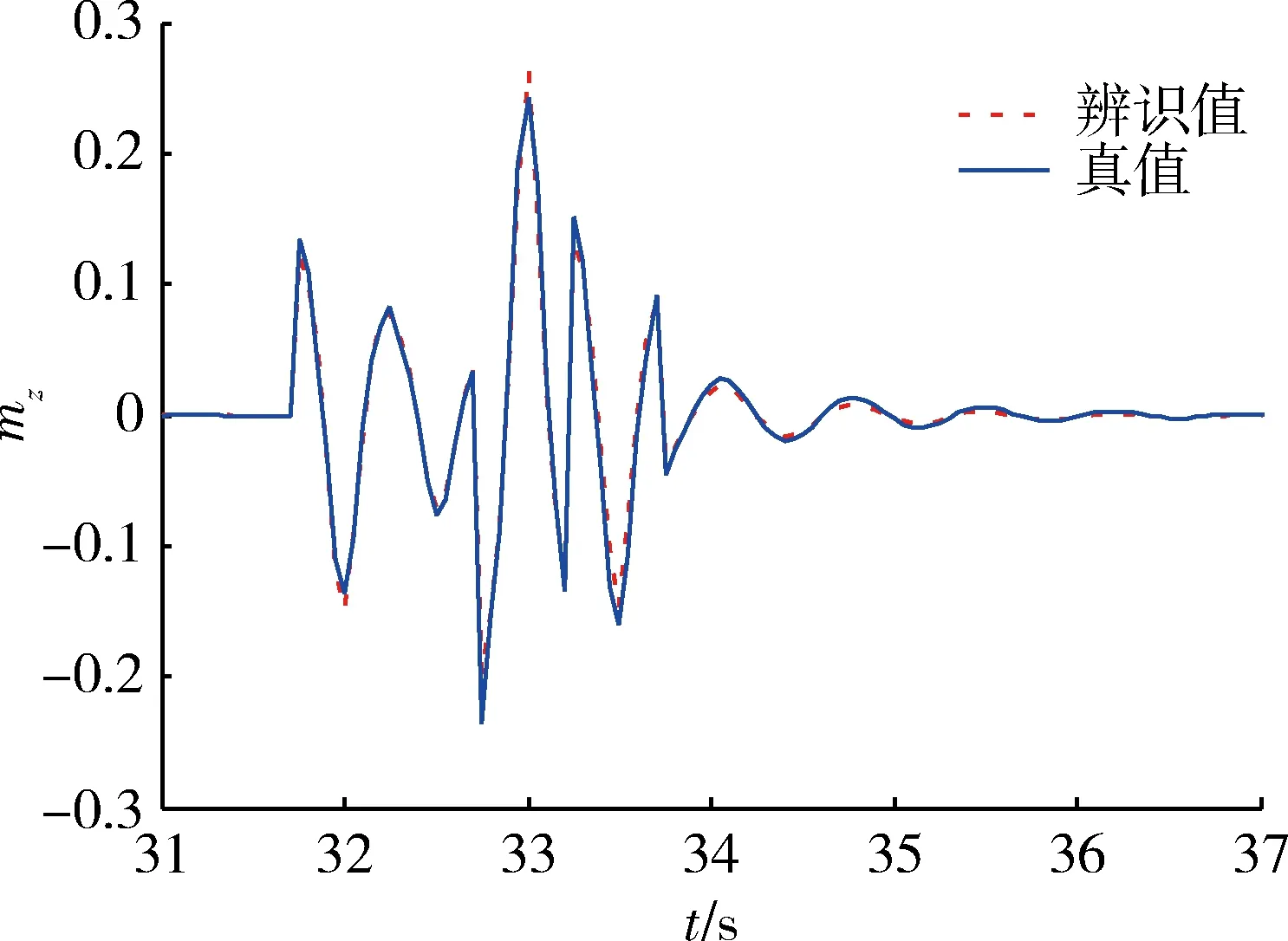
图13 “211”多级方波俯仰力矩系数辨识结果Fig.13 Identification results of pitching moment coefficient using “211”multistep square wave input
表4给出了各输入信号对俯仰力矩系数辨识的相对误差。在持续时间6 s的辨识窗口中,3种输入辨识结果的平均相对误差均超过了8%。俯仰力矩系数总体辨识精度略逊于轴向力系数和法向力系数,这说明俯仰力矩系数的气动力模型有一定的改进潜力。

表4 俯仰力矩系数辨识相对误差Table 4 Relative error of pitching moment coefficient identification
5 结束语
本文设计了3种输入指令,在(8 km,2Ma)条件附近,通过开环飞行弹道仿真试验获取了相关试验数据,针对一种改进的纵向三自由度非线性多项式气动力模型,采用递推最小二乘法对气动参数进行了辨识,比较了3种不同输入的气动参数辨识精度。
辨识结果表明,对于轴向力系数,单极方波指令辨识效果较好。对于法向力系数和俯仰力矩系数,3种输入的辨识效果接近。在开环飞行试验中,单级方波,偶极方波,“211”多级方波3种输入用于气动参数辨识是可行的。
辨识结果验证了纵向三自由度气动力模型的有效性,参数辨识的相对误差表明法向力系数模型和俯仰力矩系数模型仍有改进的空间。
[2] 蔡金狮.飞行器气动参数辨识进展[J].力学进展,1987,17(4):467-478.
CAI Jin-shi.Advances in Identification of Aircraft Aerodynamic Parameters[J].Advances in Mechanics,1987,17(4):467-478.
[3] 于君彩.飞行数据处理与气动参数辨识[D].西安:西北工业大学,2007.
YU Jun-cai.Flight Data Processing and Aerodynamic Parameter Identification[D].Xi’an :Northwestern Polytechnical University,2007.
[4] 张天姣.闭环控制战术导弹气动参数辨识技术研究[D].绵阳:中国空气动力研究与发展中心,2010.
ZHANG Tian-jiao.Aerodynamic Parameter Identification Technology of Closed-Loop Controlled Tactical Missiles[D].Mianyang:China Aerodynamics Research and Development Center,2010.
[5] SHAFER M F.Flight Investigation of Various Control Inputs intended for Parameter Estimation[C]∥The 11th Atmospheric Flight Mechanics Conference,Seattle,USA,August,1984:21-23.
[6] KRINGS M,HENNING K,THIELECKE F.Flight Test Oriented Autopilot Design for Improved Aerodynamic Parameter Identification[C]∥The 2nd CEAS Specialist Conference on Guidance,Navigation and Control,Delft,Netherland,April,2013:11-12.
[7] ALBISSER M,DOBRE S,BERNER C,et al.Identifiability Investigation of the Aerodynamic Coefficients from Free Flight Tests[C]∥AIAA Atmospheric Flight Mechanics Conference,Boston,USA,August,2013:19-22.
[8] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2011.
QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Missile Flight Dynamics[M].Beijing:Beijing Institute of Technology Press,2011.
[9] 蔡金狮.动力学系统辨识与建模[M].北京:国防工业出版社,1991.
CAI Jin-shi.Dynamic System Identification and Modeling[M].Beijing:National Defence Industry Press,1991.
[10] James E Kain,Charles M Brown,Jang G Lee.Missile Aerodynamic Parameter and Structure Identification from Flight Test Data[R].Florida:Air Force Armament Laboratory,1977:ADA056343.
[11] HALL W E,VINCENT J R.Flight Test Design for CH-47 Parameter Identification[R].NASA Contractor Report,1978:141-148.
[12] TLIFF K W.Parameter Estimation for Flight Vehicle[J].Guidance and Control,1989,12(5):608-622.
[13] 王晓鹏,焦天峰,李响.战术导弹气动参数辨识仿真[C]∥第14届中国系统仿真技术及其应用学术年会,三亚,2012:802-806.
WANG Xiao-peng,JIAO Tian-feng,LI Xiang.Simulation of Aerodynamic Parameter Identification for Tactical Missile[C]∥The 14th Chinese Conference on System Simulation Technology & Application,Sanya,2012:802-806.
[14] 强明辉,张京娥.基于MATLAB的递推最小二乘法辨识与仿真[J].自动化与仪器仪表,2008(6):4-5.
ZHANG Ming-hui,ZHANG Jing-e.Recursive Least Squares Identification and Simulation Based on MATLAB[J].Automation and Instrumentation,2008(6):4-5.
[15] 候媛彬,汪梅.系统辨识及其MATLAB仿真[M].北京:科学出版社,2004.
HOU Yuan-bin,WANG Mei.System Identification and MATLAB Simulation[M].Beijing:Science Press,2004.
[16] 汪清,钱炜祺,何开锋.导弹气动参数辨识与优化输入设计[J].宇航学报,2008,29(3):789-793.
WANG Qing,QIAN Wei-qi,HE Kai-feng.AerodynamicParameter Identification and Optimal Input Design for Missile[J].Journal of Astronautics,2008,29(3):789-793.
[17] 徐秀峰.高超声速飞行器闭环气动参数辨识[D].哈尔滨:哈尔滨工业大学,2014.
XU Xiu-feng.Closed-Loop Identification of Aerodynamic Parameters for Hypersonic Vehicle[D].Harbin:Harbin Institute of Technology,2014.
[18] 李超.高超声速飞行器气动参数辨识和输入设计技术研究[D].厦门:厦门大学,2014.
LI Chao.Research on Aerodynamic Parameter Identification and Input Design for Hypersonic Vehicle[D].Xiamen:Xiamen University,2014.
InputDesignfortheAerodynamicParametersIdentificationofTacticalMissile
YANG Chuang,ZHANG Zhen
(Beijing Institute of Electronic System Engineering,Beijing 100854,China)
In order to study the influence of input design on accuracy of aerodynamic parameters identification whenh=8 km,Ma=2 in flight test, three open-loop commands of control surface deflection based on square wave signal are designed. In the open-loop flight trajectory simulation test, recursive least squares method is used to estimate the parameters of nonlinear aerodynamic model. The aerodynamic parameters identification results show that it is feasible to use three inputs including single square wave, double square wave, “211” multistep square wave. The identification accuracy is acceptable. The longitudinal aerodynamic model of three degrees of freedom used for identification is effective.
tactical missile; aerodynamic parameter identification; input design; recursive least squares; aerodynamic model; flight test
2017-01-03;
2017-02-06
有
杨闯(1992-),男,陕西咸阳人。 硕士生,主要研究方向为飞行器总体设计。
通信地址:100854 北京142信箱30分箱E-mail:505511790@qq.com
10.3969/j.issn.1009-086x.2017.05.007
TJ761.1;V417+.1
A
1009-086X(2017)-05-0035-07

