基于IDMS的航空发动机砂尘吸入物定量监测

孙见忠， 刘信超， 刘若晨， 康远荣， 殷逸冰， 左洪福

南京航空航天大学 民航学院， 南京 210016

基于IDMS的航空发动机砂尘吸入物定量监测

孙见忠*， 刘信超， 刘若晨， 康远荣， 殷逸冰， 左洪福

南京航空航天大学 民航学院， 南京 210016

针对航空发动机砂尘吸入物定量监测的问题，提出了基于进气监测系统(IDMS)的砂尘吸入物质量浓度监测及总量估算方法。借助ANSYS电磁场仿真软件建立了IDMS系统有限元模型，实现对发动机实际工况下的砂尘吸入物的静电场模拟，研究确定砂尘吸入物质量浓度、荷质比等宏观参数与IDMS监测信号的关系。研究发现所建立的IDMS有限元模型获得的传感器特性与前期试验获得的结论一致，静电信号随吸入颗粒物浓度的变化与试验中实测信号的变化趋势一致，为基于IDMS信号的砂尘吸入物定量监测和评估提供理论依据。仿真试验表明，荷质比一定的情况下IDMS感应电荷量与砂尘浓度呈线性增长关系，通过IDMS感应电荷信号可实时监测发动机砂尘吸入物质量浓度，并可进一步累积估算一段时间内砂尘吸入物总量，最终总量估计误差不超过4%。

航空发动机； 砂尘吸入物； 静电监测； 有限元分析; 荷质比

飞机在起飞、着陆、地面试车和飞行中，动力装置往往会吸入由风或飞机尾迹扬起的漂浮于空气中的砂粒或灰尘，这些砂尘吸入物不仅影响动力装置的性能，甚至影响其可靠性[1]。针对发动机砂尘吸入物的影响问题，美国制定了砂尘环境和发动机吞砂试验等相关标准，国内参考美军标也制定了国军标GJB 2046—94、GJB 150.12A—2009等规范和要求，对发动机及其附件提出了吞砂和砂尘环境试验要求[2-3]。

为确定发动机长期工作在砂尘环境中的工作能力，世界各国纷纷开展研究，并将吞砂试验列为新型发动机设计定型的考核项目。研究证明，发动机吸入大量砂尘会造成压气机叶片严重的磨蚀，使发动机推力降低，耗油率升高。Ghenaiet等在轴流式压气机上的试验表明，6 h吞砂试验足以造成压气机效率降低7%[4]。某型直升机在中国北方使用600 h后，因压气机气流通道堵塞原因使发动机的排气温度升高20～30 ℃[1]。砂尘进入轴承封严、转动部件内壁等内部气路，会使发动机某些零部件磨损、破坏转子平衡，砂尘随冷却空气进入涡轮叶片容易堵塞冷却气孔，从而影响冷却效果导致叶片烧蚀。中国某型发动机因涡轮冷却气孔堵塞而多次发生涡轮叶片烧蚀故障，导致提前更换发动机，造成了巨大的经济损失[1]。欧美国家非常重视砂尘对发动机性能和可靠性的影响，并开展了大量仿真和试验研究，涉及整机试验[4]、加速磨损试验[5-6]以及内部冷却通道堵塞试验[7-8]等。Walsh等研究表明，在不同的情况下，涡轮叶片由于冷却孔的堵塞可导致冷却效率下降10%[7]。Cardwell[8]和Ogiriki[9]等针对冷却孔堵塞对涡轮叶片冷却效果的影响进行了详细分析，评估了叶片冷却效率的下降对叶片蠕变寿命的影响，结果表明叶片冷却效率降低15%时涡轮叶片蠕变寿命缩短高达31%。

砂尘吸入物对军、民用发动机性能及可靠性的影响受到越来越多的重视，如何定量监测及评估实际运行环境下发动机砂尘吸入物及其影响是发动机健康监测技术领域的新课题。现有发动机状态监测系统不具备监测发动机砂尘等吸入物的能力，美军方提出了发动机砂尘吸入物机载监测传感器系统的需求并开展了相关研究，其中P&W/UTC公司的基于声发射原理的监测系统及Smiths公司的基于静电感应原理的监测系统被认为最具有潜力[10]。公开文献显示静电监测系统(包括进气监测系统(Ingested Debris Monitoring System， IDMS)和尾气监测系统(Engine Distress Monitoring System， EDMS))已应用在F-135发动机上[11-12]，但在吸入物监测技术方面公开文献中并没有详细报道。本文在实验室自研静电监测系统及之前相关试验研究基础上[13-17]，开展基于静电监测传感器的发动机砂尘吸入物定量监测仿真研究，提出砂尘吸入物质量浓度实时监测及吸入物总量估算方法，并通过仿真试验指导进一步物理试验的开展。

1 IDMS传感器理论模型分析与验证

航空发动机吸入物在通过IDMS的传感器前，一般经历了与空气的摩擦、相互碰撞以及与发动机管壁摩擦撞击。试验研究表明，砂尘、金属颗粒、碳颗粒等物体由于运动会带有不同极性以及不同大小的电量，在一定速度的气流携带下经过静电传感器都能产生明显的静电感应现象[13-18]。本文研究的IDMS系统采用环形静电传感器，在进气道静电试验中，将传感器安装在管道的内壁面上，探极内表面与管道内表面齐平，不干扰颗粒在管道内的流动，安装简图如图 1所示。

图1 静电传感器简图Fig.1 Diagram of electrostatic sensor

当带电量为q的单个颗粒通过探极感应区域时，根据库伦定律和高斯定理，可以求出探极上感应出的电荷量[14-16]。以环状探极几何中心为坐标原点，建立坐标系，可以求得环状传感器感应电荷量的具体表达式为

(1)

式中：Q为探极感应电荷量；D为探极径向直径；L为探极轴向长度；xq和zq分别为点电荷在空间的径向和轴向位置；θ为环状探极上积分点绕探极中心旋转的角度；F为表示方便而引入的替换参数。

由式(1)可以推导出静电传感器环状探极上的感应电荷由以下几个因素确定：点电荷带电量q，电荷在模型中所处位置xq和zq，传感器本身几何尺寸(包括轴向尺寸L、径向尺寸D)。在不考虑传感器本身物理参数的情况下，感应电荷量与颗粒带电量存在着正比关系，与电荷在空间的位置存在复杂的非线性关系，即径向越靠近探极壁面、轴向越靠近探极中心感应电荷量越大。为描述传感器感应区间在空间上的分布规律，引入空间灵敏度的概念[15]。定义空间灵敏度为在某一位置上传感器感应电荷量与点电荷的电量大小的比值。文献[14-15]借助静电传感器标定装置，控制单个油滴带电量及经过传感器的径向位置，对单点电荷传感器数学模型及传感器特性进行了试验验证，证明了其正确性。目前有关传感器特性的理论和试验研究都是以单颗粒为主[14-17]，而在发动机气路或油路静电监测的实际工况下，在某一时刻的探极敏感空间内往往存在一团带电颗粒，由于颗粒间相互作用，电场情况非常复杂，多颗粒的情况下难以建立精确的数学模型。因此本文以现有研究为基础，针对探极区域内多颗粒的情况建立基于ANSYS的IDMS有限元模型，研究传感器敏感空间中为带电颗粒团的情况下感应电荷的变化规律，建立带电颗粒团质量浓度、荷质比等宏观参数与IDMS监测信号的关系，为实现基于IDMS信号的砂尘吸入物定量监测和评估提供理论依据。

2 基于ANSYS的砂尘吸入物IDMS信号仿真

2.1 IDMS系统有限元建模

本文使用ANSYS的电磁场分析模块建立IDMS有限元模型，它在介质分布情况复杂或不规则边界的电磁场问题求解中，能够突破电磁场边界形状的限制，简化不同介质分界面的处理，快速求解相应的电磁场问题。砂尘吸入物颗粒尺寸相比进气道直径很小，因此荷电颗粒可以等效为点电荷，可用静电场的Possion方程与Dirichlet边界条件来描述荷电颗粒与静电传感器之间的相互作用[13]，其表达式为

(2)

式中：φ(x,y,z)为场域内的电势分布；ΓP为接地管道内壁，电势为0；ΓE为作为等势体的环状电极，电势为常数；ρ(x,y,z)为场域内的体电荷分布；ε0为真空介电常数；E∞为无穷远处的电场强度，其值为0。根据静电场理论，若已知电荷密度ρ(x,y,z)分布情况和边界条件，则感应区域内的电场分布E(x,y,z)是唯一确定的，根据高斯定理可得圆环电极的感应电荷值Q为

(3)

式中：S为圆环电极的内表面积；G(x,y,z)为S上的电通量分布；ds为面积微元。由于式(3)计算复杂，因而采用有限元仿真的方法计算圆环电极上的感应电量。

IDMS系统有限元仿真模型的建立基于以下几个物理区域：模拟进气道砂尘颗粒大小及空间位置分布的空间区域、圆环静电传感器电极区域以及传感器外壳和管道壁区域。具体建模分为以下2步：

步骤1建立有限元模型。静电传感器的电极是一个环形导体，选择圆环电极的轴向为模型整体笛卡儿坐标系的z轴，径向为x轴，建立模型如图2所示，管道长度为240 mm，管道壁直径与感应电极内径同为100 mm，感应电极轴向(z轴)长度为10 mm。在对三维静电场进行有限元分析时，根据传感器模型的结构特点以及计算精度要求，选择20节点三维六边形单元SOLID121。采用映射网格划分，生成六边形有限元单元，提高计算精度。

步骤2施加载荷和求解。施加载荷是将实际模型中所受边界条件和外部或内部作用函数等效施加在有限元模型上。实际中管道壁接地，因此模型中管壁部分施加电压边界约束，设置为零电位。实际探测中电极是导电性很好的导体，受感应电场激发后内表面为等势面，因此有限元模型中电极部分各节点电势相等，需把各个节点自由度耦合，使其电势相等。电场分析中，带电颗粒视为点电荷，需要根据外来物的粒径和数目变化点电荷施载的位置和密度，在空间域划分的网格节点上根据带电颗粒的空间位置及带电量大小施加电荷载荷。ANSYS电磁场模块的静电场分析得到的基本解是各个节点的电势，因此需要用通用后处理器对结果进行处理，获得各电极各个节点的场强情况。由于电极内表面为等势面，并且只有内外表面间电极法向的电荷运动影响各等势面上的感应电荷量，因而提取感应电极的法向电场强度值计算电极上的感应电荷量。

图2 IDMS三维仿真模型及网格划分示意图Fig.2 Diagram of IDMS three-dimensional simulation model and mesh generation

在建立起IDMS有限元模型后，根据目前已有的理论分析和试验研究结论[14-19]，对IDMS有限元模型进行了验证。利用上述IDMS有限元模型，模拟点电荷带不同电量、从不同径向位置通过模型敏感空间，对产生的感应电荷进行仿真计算，可得到传感器感应电荷量随颗粒带电量、径向位置的变化(见图3)及传感器的空间灵敏度分布(见图4，图中R为电荷径向位置)。由图3 和图4的结果可见，IDMS有限元仿真模型计算得到的传感器特性与理论分析及标定试验验证得到的结果是一致的[14-19]，验证了本文所建有限元模型的准确性。

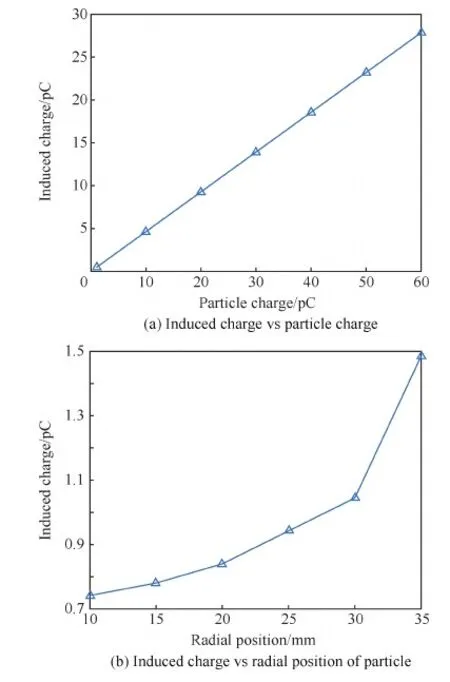
图3 IDMS感应电荷随颗粒带电量及径向位置的变化Fig.3 IDMS induced charge vs particle charge and its radial position

图4 IDMS传感器空间灵敏度Fig.4 Spatial sensitivity of IDMS sensor

2.2 砂尘颗粒带电与尺寸分布模拟

2.2.1 砂尘颗粒带电模拟

自然界中砂尘带电现象一直以来得到广泛的关注，在微观层面对砂尘带电的机理、带电量大小的研究目前尚处于起步阶段，虽已有各种学说来解释这一现象但尚无可普遍接受的定论[20]。在宏观层面众多学者展开了包括空间电荷密度、荷质比以及带电极性等物理量的试验观测，取得了一些具有重要价值的数据和结论，为本文砂尘颗粒带电模拟提供了重要参考。

1) 砂尘带电极性

研究发现自然界中砂尘所带正电荷还是负电荷同砂尘粒径有很大关系，一般来说，大砂尘带正电荷，小砂尘带负电荷。Greeley和Leach[21]通过风洞试验，给出的临界粒径为60 μm，即粒径大于60 μm 时颗粒带正电，小于60 μm时带负电，而Zheng等[22]则发现这一临界粒径值为250 μm。后来的研究结果表明：对不同地区的砂样，其临界粒径是有所不同的。

2) 砂尘荷质比

目前砂尘电荷量的试验测量主要关注的是宏观层面砂尘荷质比的测量，即单位重量砂尘所带的平均电荷量。砂尘荷质比的测量目前已有比较成熟的技术，通常可借助法拉第筒收集砂尘，通过静电计记录收集的砂尘带电量并称重即可得到平均荷质比[23]。Schmidt等[24]首次开展了砂尘荷质比的测量试验，其结果表明粒径为250 μm砂尘平均荷质比为66 μC/kg，黄宁和郑晓静[23]开展了比较系统的荷质比研究，粒径为0～1 000 μm的砂尘，其荷质比为-124～0.95 μC/kg。

对于单个颗粒物的荷电量，Jones等[25]研究发现颗粒的荷电量与颗粒等效粒径存在指数关系，可表示为

(4)

式中：Qp是颗粒的荷电数量，单位为等效电子数；α是与颗粒本身属性和所处的环境有关的常数；Dp是颗粒的等效粒径，单位为μm；γ为试验确定的常数，大小在1.2～1.6之间。

2.2.2 砂尘颗粒尺寸分布模拟

自然界中砂尘主要成分是石英，GB/T 4797.2013—95根据不同的空气动力学特性，将直径大小在1～150 μm之间的颗粒定义为尘，直径在150～1 000 μm 之间的颗粒定义为砂[19]。尘和砂颗粒尺寸大小的近似分布如图5所示。

砂尘浓度，即单位体积空气中砂尘粒子的质量，是砂尘试验中的一个重要指标，大气中砂尘的浓度与地理位置、气候类型及人类活动有较大关系，如GB/T 4797.2013—95中给出自然砂尘浓度的最大值只有2 mg/m3(工业区)和17.4 mg/m3(沙漠地区)，而直升机诱发的砂尘环境浓度高达100～3 000 mg/m3[19]。GJB 150.12A—2009《军用装备实验室环境试验方法第12部分：砂尘试验》中规定对于可能会在未铺砌的路面上空飞行的直升机附近工作的装备，吹砂试验浓度为2 200 mg/m3，吹尘试验浓度为10 600 mg/m3[3]。GJB 2046—94《航空涡喷涡扇发动机吞砂试验》中规定，“除另有规定外，试验时发动机进口砂尘浓度应为每立方米空气含砂尘53 mg”[2]。

图5 砂和尘颗粒尺寸的累积分布[19]Fig.5 Cumulative distributions of size of sand and dust particles[19]

2.3 砂尘吸入物静电监测信号仿真流程

采用ANSYS电磁场仿真方法可以弥补现有物理试验平台无法精确模拟和控制砂尘颗粒带电、尺寸分布及浓度的问题，实现对不同尺寸参数、不同运动参数和不同荷电参数的砂尘吸入物的模拟，进行静电信号理论分析研究。

根据2.2节的分析，在已知砂尘浓度情况下，首先根据砂尘成分即石英的密度和砂尘颗粒的尺寸分布(见图5)得到单位体积空气中不同尺寸的砂尘颗粒的数目。进一步根据荷质比可得单位体积空气中砂尘颗粒总的带电量或电荷数，同时根据式(4)确定的不同粒径颗粒的荷电数量的比例关系，可得到不同粒径颗粒所携带的电荷数目。砂尘吸入物静电监测信号仿真步骤如下：

步骤1根据砂尘颗粒浓度确定单位体积空气中颗粒物总质量，并根据颗粒物尺寸分布，确定各尺寸等级下颗粒的总质量。

步骤2根据砂尘颗粒物质密度，确定各尺寸等级下颗粒总体积及数目。

步骤3根据砂尘荷质比确定单位体积空气中颗粒物总的带电量或电荷数。

步骤4已知砂尘总的颗粒数和总的电荷数目，根据式(4)可得到不同粒径颗粒所携带的电荷数目。

步骤5在砂尘颗粒空间区域中随机分布颗粒，不同粒径颗粒携带不同电荷数，模拟发动机进气道吸入的砂尘。

步骤6在ANSYS环境下，所有砂尘颗粒随气流沿z轴方向每步移动一个网格距离，并判断位于IDMS传感器敏感空间中的砂尘颗粒集。

步骤7根据敏感空间中颗粒携带的电荷量及其空间位置，对IDMS有限元模型施加电荷载荷，提取感应电极的法向电场强度值，计算电极上的感应电荷量。

模拟小颗粒砂尘(粒径≤150 μm)环境浓度为53 mg/m3，荷质比为-100 μC/kg，则根据以上仿真步骤可得不同尺寸砂尘颗粒数目及其携带单位电荷数(见表1)。砂尘颗团移动2 000步(每步3 mm，即2 000×3=6 000 mm)所得的IDMS感应电荷信号如图6(a)所示。若假设砂尘颗粒随气流移动速度为15 m/s，测量电路等效电阻为1 ΜΩ，则仿真得到的电压信号如图6(b)所示。

表1不同尺寸砂尘颗粒数目及电荷数(浓度:53mg/m3，荷质比:-100μC/kg)

Table1Numberandassociatedchargeofsandparticlesofdifferentsizes(Concentration:53mg/m3，charge-to-massratio:-100μC/kg)

Diameterofparticles/μmNo.ofparticlesAverageNo.ofcharges1-15120145352415-30288182043830-4554014628045-6017687928660-7575311853075-9040016340690-105245213476105-120170268401120-135123327912135-150108391782

图6 感应电荷信号和输出电压信号Fig.6 Induced charge and output voltage signals

图6通过ANSYS仿真得到的感应电荷信号与电压信号，与文献[14]物理试验中采集的信号在同一数量级上，感应电荷为pC级别，电压值为mV级别，具体数值的差异与试验中采用的颗粒物浓度及其荷质比有关。此外，在颗粒浓度为53 mg/m3，荷质比为-100 μC/kg的情况下，仿真计算得到式(4)中α值为140，这与文献[25]中得出的α在1～100之间基本吻合，从另一角度也反映了IDMS有限元模型的合理性。实际静电信号受颗粒物浓度、颗粒荷电数以及速度等因素影响，现有试验台无法有效精确控制这些变量，这也是目前静电监测技术进一步深入研究的瓶颈。因此，本文利用有限元技术构建IDMS监测系统的仿真平台，实现输入变量的可控，进而可以模拟各种工况及故障注入，定量分析静电监测系统的特性及故障信号特征值，可进一步指导物理验证试验的开展。

3 砂尘吸入物浓度实时监测与总量估算仿真试验

3.1 砂尘吸入物仿真试验及数据分析

按照2.3节的砂尘吸入物仿真方法，模拟仿真了不同浓度和荷质比砂尘吸入物(见表2)情况下产生的IDMS信号，每种浓度环境下仿真总共2 000步，步长为3 mm，模拟进气道砂尘颗粒所处的空间区域为一长度为6 000 mm、直径为100 mm 的圆柱体。

为研究砂尘吸入物浓度与IDMS感应电荷的关系，统计仿真中每一步得到的敏感空间内砂尘颗粒总数、总体积及相应的感应电荷量，如图7所示为砂尘浓度为59 mg/m3时感应电荷量与颗粒总数及总体积的关系。由图7可见，模拟的进气道砂尘颗粒所处的空间区域内平均砂尘浓度是一定的(59 mg/m3)，但由于颗粒在空间分布的随机性，因此敏感空间内某一时刻颗粒的总数目和体积(或浓度)是不断波动的(见图8，图中仿真砂尘环境浓度为59 mg/m3)，因此其产生的感应电荷量也是不断变化的(见图6)。同时，图7表明敏感空间内相同数目或相同体积的颗粒感应出的电荷量是不同的，主要原因有2个：① 颗粒大小不一，携带的静电荷不一样，即使数目相同，空间内砂尘颗粒总的带电量也不一样；② 颗粒在空间分布的随机性，即使同样数量和尺寸的颗粒也会产生不一样的感应电荷。进一步对图7中数据作相关性分析表明，感应电荷量与颗粒数目和体积均存在明显的相关性(分别为0.77和0.71)，后续分析中将以敏感空间中砂尘颗粒物质量浓度为主。

表2 小颗粒砂尘环境模拟参数Table 2 Simulation parameters of small sand particles environment

图7 感应电荷量与敏感空间内砂尘颗粒总数及总体积的关系(砂尘浓度：59 mg/m3)Fig.7 Induced charge vs total particle number and volume in sensitive zone (Concentration: 59 mg/m3)

图8 敏感空间砂尘质量浓度变化Fig.8 Mass concentration variation of sand particles in sensitive zone

对不同浓度和不同荷质比情况下小颗粒砂尘环境仿真得到的数据进行分析，得到IDMS感应电荷量与敏感空间砂尘质量浓度关系如图9所示。由图9可见，相同荷质比情况下，随着砂尘浓度的升高，IDMS感应电荷量会增加，而同等砂尘浓度下随着砂尘荷质比的升高，感应电荷量也会增加。同时，由图9可见在浓度与荷质比一定的情况下，感应电荷量存在一定波动，如上所述这主要由于砂尘颗粒尺寸及空间位置分布的随机性所致。对相同荷质比情况下感应电荷量与砂尘浓度数据进行拟合，得到的线性关系为

图9 IDMS感应电荷与敏感空间砂尘质量浓度关系Fig.9 Relationship between IDMS induced charge and particle mass concentration of sensitive zone

(5)

式中：C为砂尘质量浓度；q/m为荷质比。式(5)所确立的线性关系为利用IDMS感应电荷量来实时监测发动机砂尘吸入物质量浓度提供了理论依据。

3.2 砂尘浓度实时监测方法

为验证上述基于IDMS系统的发动机砂尘吸入物浓度监测方法，模拟发动机进气道依次吸入不同浓度的小颗粒物砂尘团，C=0.03，0.025，0.04，0.05 g/m3，气流速度为15 m/s，IDMS信号采样频率为5 000 Hz，则通过ANSYS仿真产生的IDMS感应电荷信号如图 10所示。由图 10可见感应电荷信号整体上随吸入砂尘颗粒物浓度而波动，这一结论与文献[14]试验结果一致，即随着颗粒物浓度增大，感应电荷量或活动率水平(文献[14]计算的活动率水平是在一定的时间内感应电荷量信号的均方根值)也相应增加。但即使同一浓度的颗粒物砂尘团在吸入发动机经过传感器的敏感空间时，由于颗粒物空间分布的随机性导致实际得到的感应电荷信号具有较大的波动性。

图10 IDMS感应电荷仿真信号Fig.10 Simulation of IDMS induced charge signals

在得到IDMS感应电荷信号后，即可根据式(5)来估计颗粒物的浓度。图11同时给出了质量浓度的估计值和实际值，由于感应电荷信号的波动性，根据式(5)得到的质量浓度估计值同样具有明显的波动性。

图11所示浓度估计值与实际值偏差的存在是由于3.1节式(5)在建立时就不可避免地存在一定的误差，由于砂尘颗粒在敏感空间分布的随机性决定了式(5)建立的质量浓度和感应电荷量的关系带有一定的随机误差(见图9)，因此在根据感应电荷量来估算颗粒物浓度时也带有一定的误差，误差有时为“负”，有时为“正”(见图12)，但总体上与颗粒物浓度的变化趋势一致。

图11 砂尘颗粒物质量浓度估计值与实际值Fig.11 Sands particle mass concentration estimation and real values

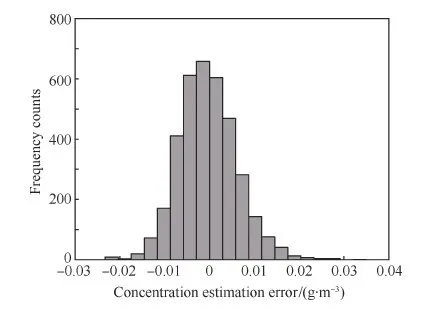
图12 砂尘颗粒物浓度估计误差Fig.12 Estimation error of sand particle concentration

3.3 砂尘吸入物总量估算方法

若已知发动机进气道气流速度和截面积，则可以根据实时监测的颗粒物质量浓度进一步估计某一段时间吸入物总质量M，其表达式为

(6)

式中：Ci为第i次取样时的质量浓度；N为某一段时间T内质量浓度采样总次数；f为信号采样频率(N=fT)；v为气流速度；Ssec为管道截面积。根据式(6)和图 10所示的IDMS感应电荷量信号分别估计进气道吸入的4个不同浓度砂尘团的总质量，结果如图 13所示，图中虚线表示估计值与实际值相等的情况。

图13给出了不同IDMS信号采样频率下估算得到的颗粒物质量与实际质量的对比，图13结果显示采样频率对总质量估计结果影响不大，吸入物总量估计值均比较接近实际值。采样频率越高，单位时间内采样次数越多，意味着测量吸入物质量浓度的空间分辨率越高，采样得到的质量浓度数据越多，越逼近吸入物的实际浓度值。在本文的仿真试验中，依次通过传感器的4个浓度颗粒团的时间均为0.18 s，理论上每0.18 s内颗粒浓度变化不是很明显，近似估计浓度最少可以每0.18 s内采样一次即可(即采样频率为约6 Hz)。因此，实际中采样频率多少取决于宏观上砂尘吸

入物浓度空间变化的情况，在空间上变化越大，采样频率应提高。虽然图11所示的质量浓度的估计值和实际值有较明显的波动性，但由于两者偏差具有一定的对称性(见图12)，因此在计算某一段时间内的总质量时，正负误差抵消，因此最终得到的砂尘颗粒物吸入总量误差较小。表3给出了4个不同浓度的砂尘团及整个砂尘吸入物的质量估计结果及误差，最大误差不超过13%，且随着时间段的累积，由于正负误差的抵消作用，最终总量估计误差不超过4%。

图13 砂尘吸入物总量估计结果Fig.13 Total mass estimation of ingested sand particles

表3 砂尘吸入物质量估计结果及误差Table 3 Estimation mass and error of ingested sand particles

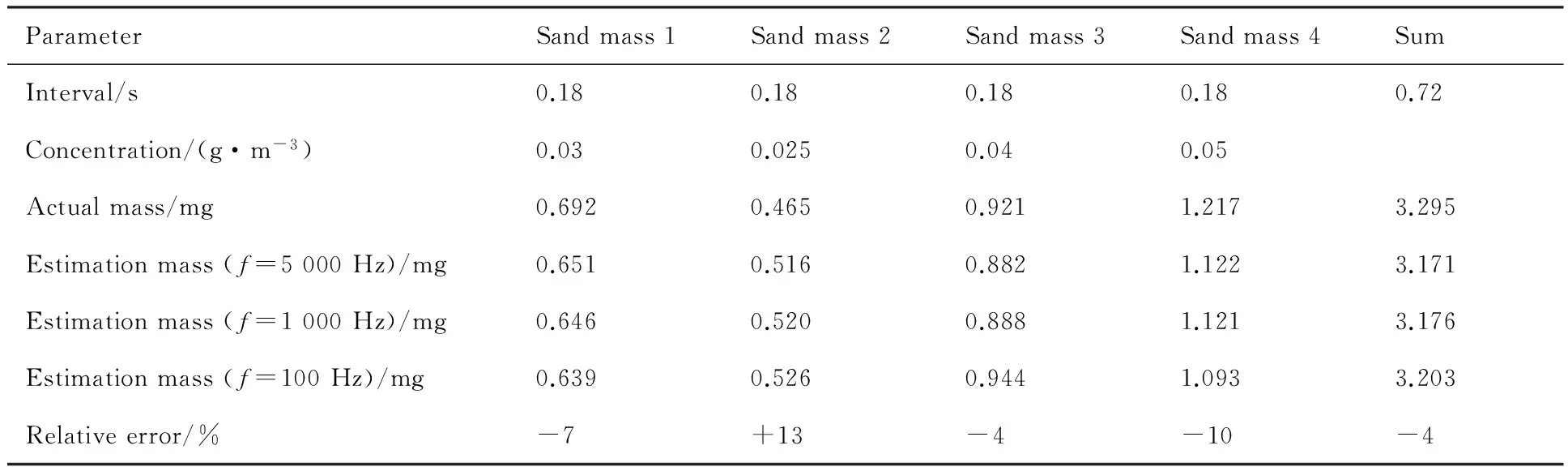
ParameterSandmass1Sandmass2Sandmass3Sandmass4SumInterval/s0.180.180.180.180.72Concentration/(g·m-3)0.030.0250.040.05Actualmass/mg0.6920.4650.9211.2173.295Estimationmass(f=5000Hz)/mg0.6510.5160.8821.1223.171Estimationmass(f=1000Hz)/mg0.6460.5200.8881.1213.176Estimationmass(f=100Hz)/mg0.6390.5260.9441.0933.203Relativeerror/%-7+13-4-10-4

4 结 论

1) 仿真试验表明，本文建立的IDMS有限元模型获得的传感器特性与前期试验获得的结论一致，仿真静电信号随吸入颗粒物浓度的变化与试验中实测信号的趋势一致，证明了IDMS有限元模型的合理性。

2) 仿真试验表明，荷质比一定的情况下IDMS感应电荷量与砂尘浓度呈线性增长关系。

3) 通过IDMS感应电荷信号可实时监测发动机砂尘吸入物质量浓度，估计值与实际浓度值表现出较好的一致性，进一步可累积估算一段时间内砂尘吸入物总量，且随着时间段的延长，由于正负误差的抵消作用，最终总量估计误差不超过4%。

本文研究所确立的IDMS感应电荷信号与吸入物质量浓度的线性关系为利用IDMS感应电荷量来实时监测发动机砂尘吸入物质量浓度提供了理论依据，同时也为后续吸入物静电监测试验台的改进及物理试验的开展提供了借鉴。

[1] 章伟, 郭徽. 浅谈灰尘对直升机动力装置性能和可靠性的影响[C]//湖南国防科技论坛. 湖南： 湖南省兵工协会, 2009: 451-454.

ZHANG W, GUO H. Influence of dust on the performance and reliability of helicopter power plant[C]//Hunan National Defence Science and Technology Forum. Hunan: Hunan Ordnance Association, 2009： 451-454 (in Chinese).

[2] 国防科学技术工业委员会. 航空涡喷涡扇发动机吞砂试验： GJB 2046—94[S]. 北京: 中国航空综合技术研究所, 1994.

Committee of Defense Industry of Science and Technology. Swallowing sands tests of turbojet and turbofan engines： GJB 2046—94[S]. Beijing: AVIC China Aero-Polytechnology Establishment, 1994 (in Chinese).

[3] 中国人民解放军总装备部. 军用装备实验室环境试验方法第12部分： 砂尘试验： GJB 150.12A—2009[S]. 北京: 总装备部军标出版发行部, 2009.

General Armament Department of PLA. 12th part of environmental test methods for military equipment: Sand dust test： GJB 150.12A—2009[S]. Beijing: General Armament Department Military Label Publishing Department, 2009 (in Chinese).

[4] GHENAIET A, ELDER R L, TAN S C. Particles trajectories through an axial fan and performance degradation due to sand ingestion: 2001-GT-0497[R]. New York: ASME, 2001.

[5] DUNN M G, PADOVA C, MOLLER J E, et al. Performance deterioration of a turbofan and a turbojet engine upon exposure to a dust environment[J]. Journal of Engineering for Gas Turbines & Power, 1987, 109(3): 336-343.

[6] HAMED A A. Turbine blade surface deterioration by erosion[J]. Journal of Turbomachinery, 2004, 127(3): 445-452.

[7] WALSH W S, THOLE K A, JOE C. Effects of sand ingestion on the blockage of film-cooling holes[C]//Turbomachinery Technical Conference and Exposition 2006. New York: ASME, 2006: 81-90.

[8] CARDWELL N D, THOLE K A, BURD S W. Investigation of sand blocking within impingement and film-cooling holes: 2008-GT-51351[R]. New York: ASME, 2001.

[9] OGIRIKI E, THANK-GOD I, GOWON S. Effect of fouling, thermal barrier coating degradation and film cooling holes blockage on gas turbine engine creep life[J]. Procedia Cirp, 2015, 38: 228-233.

[10] SCALA S, KONRAD M, MASON R, et al. Sensor requirements to monitor the real time performance of a gas turbine engine undergoing compressor blade erosion: AIAA-2004-3548[R]. Reston, VA: AIAA, 2004.

[11] POWRIE H E G, FISHER C E. Monitoring of foreign objects ingested into the intake of a jet engine[C]//International Conference on Condition Monitoring. Swansea: University of Wales, 1999: 175-190.

[12] POWRIE H E G, FISHER C E. Engine health monitoring: Towards total prognostics[C]//Aerospace Conference. Piscataway, NJ: IEEE Press, 1999: 11-20.

[13] 文振华, 左洪福, 李耀华. 气路颗粒静电监测技术及实验[J]． 航空动力学报, 2008, 23(12): 2321- 2326．

WEN Z H, ZUO H F, LI Y H. Gas path debris electrostatic monitoring technology and experiment[J]. Journal of Aerospace Power, 2008, 23(12): 2321-2326 (in Chinese).

[14] 殷逸冰, 左洪福, 冒慧杰, 等. 航空发动机进气道静电传感器空间模型解析及感应信号影响因素实验分析[J]. 仪器仪表学报, 2015, 36(4): 795-803.

YIN Y B, ZUO H F, MAO H J, et al. Spatial analysis of inlet electrostatic sensor and experimental study on influence factors of charge-induced signal[J]. Journal of Instrument and Meter, 2015, 36(4): 795-803 (in Chinese).

[15] 殷逸冰, 左洪福, 文振华, 等. 航空发动机吸入颗粒物静电感应特性的模拟实验及分析[J]. 航空学报, 2015, 36(2): 691-702.

YIN Y B, ZUO H F, WEN Z H, et al.Electrostatic induction characteristics of aeroengine inhaled particles: Simulated experiment analysis[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 691-702 (in Chinese).

[16] 冒慧杰, 左洪福, 黄文杰, 等. 航空新型静电传感器建模与标定实验[J]. 航空学报, 2016, 37(7): 2242-2250.

MAO H J, ZUO H F, HUANG W J, et al. Mathematical modeling and calibration experiment of new electrostatic sensor in aviation[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2242-2250 (in Chinese).

[17] LIU R C, ZUO H F, SUN J Z, et al. Simulation of electrostatic oil line sensing and validation using experimental results[J]. Tribology International, 2017, 105: 15-26.

[18] 李耀华, 左洪福, 文振华. 航空发动机气路颗粒静电监测技术模拟实验[J]. 航空学报, 2009, 30(4): 604-608.

LI Y H, ZUO H F, WEN Z H. Simulated experiment of aircraft engine gas path debris monitoring technology[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(4): 604-608 (in Chinese).

[19] 中国国家标准化管理委员会. 环境条件分类·自然环境条件·尘、沙、盐雾： GB/T 4797.2013—95[S]. 北京: 中国标准出版社, 2013.

China National Standardization Administration Committee. Classification of environmental conditions-natural conditions-dust, sand, salt fog： GB/T 4797.2013—95[S]. Beijing: China Standard Press, 2013 (in Chinese).

[20] 郑晓静, 黄宁, 周又和. 风沙运动的沙粒带电机理及其影响的研究进展[J]. 力学进展, 2004, 34(1):77-86.

ZHENG X J, HUANG N, ZHOU Y H. Advances in investigation on electrification of wind-blown sands and its effects[J]. Advances in Mechanics, 2004, 34(1): 77-86 (in Chinese).

[21] GREELEY R, LEACH R. A preliminary assessment of the effects of electrostatics on aeolian processes: NASA TM-79729-236[R].Washington, D.C: NASA, 1978.

[22] ZHENG X J, HUANG N, ZHOU Y. Laboratory measurement of electrification of wind-blown sands and simulation of its effect on sand saltation movement[J]. Journal of Geophysical Research: Atmospheres, 2003, 108(D10): 1-9.

[23] 黄宁, 郑晓静. 风沙流中沙粒带电现象的实验测试[J]. 科学通报, 2000, 45(20): 2232-2235.

HUANG N, ZHENG X J. Experimental study on charged phenomena of sand grains in wind blown sand[J]. Chinese Science Bulletin, 2000, 45(20): 2232-2235 (in Chinese).

[24] SCHMIDT D S, SCHMIDT R A, DENT J D. Electrostatic force on salting sand[J]. Journal of Geophysical Research: Atmospheres, 1998, 103(D8): 8997-9001.

[25] JONES A D, JOHNSTON A M, VINCENT J H. The measurement of electric charge on airborne dusts in quarries and mines[J]. Staub Reinhaltung Der Luft, 1985, 45(10): 475-480.

(责任编辑： 王娇)

*Correspondingauthor.E-mail:sunjianzhong@nuaa.edu.cn

IDMSbasedmethodforquantitativemonitoringofaero-engineingestedairbornesands

SUNJianzhong*,LIUXinchao,LIURuochen,KANGYuanrong,YINYibing,ZUOHongfu

CollegeofCivilAviation,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

Inordertomonitortheingestedairbornesandsinsidetheaero-enginequantitatively,thispaperbuildsthesimulationmodelbasedoningesteddebrismonitoringsystem(IDMS)toanalyzedifferentingestedairbornesanddistributionsandalsoproposesthemethodforestimatingthetotalamountofingestedairbornesands,basedontheIDMSsignal.IDMSmodelisdevelopedinfiniteelementsoftwareANSYStosimulatetheelectrostaticfieldofingestedairbornesandswithelectrostaticcharges.TherelationshipbetweentheIDMSmonitoringsignalsandtheparametersoftheingestedairbornesandsisstudied,suchasmassconcentrationsandcharge-to-massratio.TheIDMSsensingcharacteristicderivedfromthefiniteelementmodelproposedisfoundtobeconsistentwiththeresultsofpreviousexperiments.Thetrendofelectrostaticsignalsfrombothsimulationandexperimentarethesame,layingthebasisforthemonitoringofthemassconcentrationsoftheingestedairbornesandsaswellastheestimationoftotalamount.ThissimulationstudyshowsthattherelationshipbetweeninducedchargesofIDMSandmassconcentrationislinear,givenaconstantcharge-to-massratio.Theinducedchargesalongwithdifferentingestedairbornesanddistributionscanbeextractedfromreal-timemonitoringsystem.Therefore,basedonthemeasuredchargesignalsusingtheIDMS,themassconcentrationsoftheingestedairbornesandscanberecordedon-line,andfurtherthetotalamountofairbornesandsingestedduringaspecifiedintervalcanbeestimatedwithanestimationerrornogreaterthan4%.

aero-engine;ingestedairbornesand;electrostaticmonitoring;finiteelementanalysis;charge-to-massratio

2016-11-24；Revised2016-12-07；Accepted2016-12-14；Publishedonline2016-12-281514

URL：www.cnki.net/kcms/detail/11.1929.V.20161228.1514.002.html

s：NationalNaturalScienceFoundationofChina(61403198)；NaturalScienceFoundationofJiangsuProvince(BK20140827)；AeronauticalScienceFoundationofChina(2014ZB52020)

2016-11-24；退修日期2016-12-07；录用日期2016-12-14； < class="emphasis_bold">网络出版时间

时间：2016-12-281514

www.cnki.net/kcms/detail/11.1929.V.20161228.1514.002.html

国家自然科学基金 (61403198)； 江苏省自然科学基金 (BK20140827)； 航空科学基金 (2014ZB52020)

.E-mailsunjianzhong@nuaa.edu.cn

孙见忠， 刘信超， 刘若晨， 等． 基于IDMS的航空发动机砂尘吸入物定量监测J． 航空学报,2017,38(8):320977.SUNJZ,LIUXC,LIURC,etal.IDMSbasedmethodforquantitativemonitoringofaero-engineingestedairbornesandsJ.ActaAeronauticaetAstronauticaSinica,2017,38(8):320977.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.320977

V231.25

A

1000-6893(2017)08-320977-11