内压作用下的航空轮胎爆破碎片动力响应

张帆， 郑津洋， 马利

1.浙江大学 能源工程学院， 杭州 310012 2.浙江工业大学 应用力学研究所， 杭州 310012

内压作用下的航空轮胎爆破碎片动力响应

张帆1， 郑津洋1， 马利2,*

1.浙江大学 能源工程学院， 杭州 310012 2.浙江工业大学 应用力学研究所， 杭州 310012

航空轮胎爆破时受内压释放的影响，爆破碎片的速度会有明显增加，而非与适航标准规定的与轮胎降落时的胎速相同。利用Fluent中用户自定义函数编写动力响应程序，采用动网格和用户自定义函数相结合的方法，展开内压释放作用下的轮胎爆破碎片速度动力响应特性的数值模拟研究。假设轮胎爆破失效是存在先前缺陷造成的，将碎片受冲击后的动态过程分解为内压释放冲击加速阶段和以一定初速度在空气阻力下减速运动两个阶段，提出仅考虑碎片两侧实时压力差作为动力源的简化物理爆破模型，来分析碎片的速度受内压作用的响应和整个流场压力以及速度变化情况，弥补了数学模型未考虑内外压平衡过程的不足，为预测轮胎爆破后碎片获得能量和爆破气流能量等提供数值参考，以便提出相应的安全防范措施。

航空轮胎； 爆破碎片； 流固耦合； CFD； 用户自定义函数

航空轮胎是飞机上安全性与可靠性要求极高的重要部件，随着航空工业的发展, 航空轮胎的性能不断提高, 基本适应了航空工业发展的需要。但是，由于航空轮胎使用条件苛刻，其发生爆破失效而引发的飞机偏离、冲出跑道，爆破碎片打坏机翼、击伤平尾、击漏油箱等事故发生率依旧较高[1-4]，成为目前中断飞机起飞的首要原因[3,5]，也是飞机安全航行的重大隐患。近年来，国内外航空轮胎爆破事故层出不穷，轮胎爆破本身产生的碎片以及冲击波会直接引发一系列导致人员伤亡的事故[6]，若在飞机起飞或降落过程中发生轮胎爆破，引发飞机在空中的操纵障碍，则后果不堪设想。因此飞机适航验证必须考虑轮胎爆破的风险，无论轮胎爆破发生的概率如何，均应保证飞机的飞行安全，以避免带来巨大的经济损失和不良政治影响[2,4]。

美国联邦航空局(FAA)颁布的联邦航空条例(FAR)第25部对飞机轮胎承载能力计算进行了详细说明，可是未提出对于轮胎爆破的相关计算模型以及适航验证方法；欧洲航空安全局(EASA)接替联合航空局(JAA)之前，由JAA于2002年颁布的JAA TGM/25/8《JAA Temporary Guidance Material, TGM/25/8(issue 2)Wheel And Tire Failure Model》是当时轮胎爆破适航验证的唯一指导材料，针对轮胎爆破碎片提出以机轮的最大旋转速度作为碎片飞行速度；2008年EASA替代JAA，并于2013年颁布NPA-2013.02《Noticeof Proposed Amendment》，以及之后颁布对运输类飞机轮胎爆破适航条款CS-25的修正案等，对JAA TGM/25/8内容进行更新改进，详述了轮胎爆破碎片的危害模式、爆胎空气喷流压力效应模式、甩胎模式和轮缘碎片模式这四大模型的定义，并提出爆破碎片速度与飞机轮胎额定速度一致，航空轮胎爆破模型有了进一步发展[7-8]。国内相关文献较少，其中白杰等[9]曾针对外来物损伤条件研究了轮胎爆破碎片的产生机理，并综合热力学、固体力学及材料断裂准则建立了轮胎碎片速度计算的数学模型。然而，国内外对轮胎爆破碎片速度问题的研究中均存在着一定的不足，尤其是适航验证标准中提出爆破碎片速度的确定不考虑由于轮胎内压释放带来的额外速度增量，而实际轮胎爆破所释放的巨大能量是不可忽略的，对碎片速度的影响起着重要作用[10-11]。

本文针对实际的飞机轮胎几何模型，通过计算流体力学方法，建立了空气流场中轮胎碎片响应的流固耦合动力学模型，实现轮胎爆炸过程中轮胎碎片在爆炸时飞出过程的数值模拟，预测轮胎碎片在爆破瞬时的运动状态和所具备的能量，评估其破坏能力，为建立有效预防轮胎爆破事故的对策提供理论依据。

1 航空轮胎爆破分析

飞机轮胎爆破是一种复杂的现象，碎片飞出过程实质上是由胎面碎片受轮胎内外部压力气体共同作用下，使原本轮胎薄弱的环节脱离原有位置的动力响应过程。冲击气流的变化会引起爆破周围空气流场、流场力的变化，而在流场力作用下，碎片的动力响应可能发生改变，进而流场的变化可能会有所加剧，冲击气流及流场变化和轮胎碎片是相互耦合、相互影响的，二者的互反馈作用将使碎片与空气处于特定的流固耦合形态[12]。流固耦合力学的重要特征是两相介质之间的交互作用。其基本原理涉及流体力学、固体力学、传热、传质等多个方面[13]，轮胎爆破过程属于其范畴。

对于轮胎爆破过程，将其简化为碎片突然失去各方向上物理约束，被轮胎中压缩气体冲击飞起的过程。轮胎转速对碎片初始速度的响应与碎片受内压影响而产生的冲击速度在最初始阶段是一种矢量性的叠加，在此主要研究内压对碎片速度的影响故忽略了此种耦合；轮胎爆破的失效模式假设是轮胎先前的缺陷造成的，若详细考虑轮胎材料内部的细节结构以及轮胎碎片逐渐剥离的动态损伤过程，将极大增加计算量和收敛难度，故在计算初始时刻将轮胎碎片视为与原轮胎整体不存在物理约束，仅考虑轮胎内压释放推动爆破碎片独立运动喷射过程，忽略了轮胎碎片动态剥离过程所消耗的能量对碎片速度的影响。计算方面采用Eulerian/Lagrangian混合方法，利用Fluent的可压缩、动网格流场分析功能来求解轮胎爆破后流场中气体的压力分布、速度分布等物理响应，利用Fluent的用户自定义函数 (User Defined Function, UDF)来实现求解轮胎碎片的动力响应，即速度和飞出位移，采用局部网格重划法解决了轮胎碎片的大位移问题[14]。

轮胎附近的结构复杂，故模型需要一定的简化。图1所示为航空轮胎在起落架放下时的环境示意图。其中支架会对膨胀的压缩气体流场产生一定的侧向扰动；侧面轮胎也对流场有影响，轮胎只在单侧阻挡，可能会导致轮胎碎片产生复杂的动力响应(例如碎片碰撞后的翻滚)。由于其影响并非关键因素，故模型中予以忽略，经后文分析可知，实际的响应过程主要是在初始极短的时间内发生作用的结果，以上外部环境的影响可以忽略。

轮胎碎片受到的载荷主要可以分为3种:大气外压、压缩气体的内压和附加载荷。其中内压是使轮胎碎片飞出的关键动力，外压则具有一定的反作用。另外附加载荷包括：① 轮胎材料内部本身存在的帘线结构在产生碎片后拉扯而产生的扭矩与转矩，将导致碎片的翻滚；② 碾压的外来物，可能对轮胎泄压产生影响。第①种情况下的载荷因不考虑轮胎动态剥离的过程,予以忽略，第②种附加载荷较难测定，但其力度较小、作用较慢，故模型仿真时也忽略其影响。

图1 起落架放下模式结构Fig.1 Structure of landing gear down model

2 流固耦合、Fluent动网格以及UDF二次开发技术2.1 流固耦合求解

目前针对流固耦合求解问题，从控制方程的解法上分为统一耦合解法和迭代耦合解法，二者的主要区别在于前者所有变量在同一时间步内同时求解，而后者则是在每一时间步内依次求解流体控制方程和固体动力学方程[15]，对于爆破轮胎碎片的模拟因其速度随内压变化而不断改变故采用迭代耦合解法。流固耦合求解按运动学描述分类，求解技术包括欧拉方法、拉格朗日方法和ALE(Arbitrary Lagrange-Euler)方法[16]。ALE描述能比拉格朗日描述承受更大的网格畸变，比欧拉描述提供更精细的网格解析度，但其计算量太大，因此实际计算中全ALE方法求解的方案仍不被采用[17]。采用单一类型网格以及单一类型数值方法来解决流固耦合问题是目前提高流固耦合分析精度的主流研究方向[15]。

2.2 动网格技术的网格变形与局部重构

动网格技术对包含物体变形及物体间的相对运动具有重要意义[18]，轮胎碎片边界随时间变化而引起流体发生变化，其边界位置以一定的速度变化方式发生改变，下一个时间步的运动取决于现在的时间步结果，因此需要采用动网格来实现每个时间步流体域中的网格在Fluent中的自动更新，以保证计算的连续、准确。

对于任意一个控制体V内含有运动边界的动网格模型，其满足的守恒方程为

(1)

式中：ρ为液体密度；φ为通量；μ为速度矢量；μg为运动网格的速度；A为面积向量；Γ为扩散系数；Sφ为源项；∂V为控制体的边界。将式(1)的时间导数进行一阶向后差分得

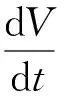
(2)

式中:上标n和n+1分别代表当前时间步和下一时间步。

为了满足网格守恒，式(2)中的dV/dt为

(3)

式中：nf为面网格数；Aj为j面的面积向量；μg,j·Aj=δVj/Δt，δVj为j面在Δt时间内形成的空间体积。

动网格的网格更新算法有3种[19]：弹簧变形法(Smoothing)、动态层法(Layering)和局部网格重构法(Remeshing)[20-21]。弹簧变形法是目前广泛应用的网格变形方法，周璇等[22]曾通过引入弹簧倔强系数的逐层改进方法，改善变形后的网格质量，并同时引入背景网格和直接插值法，提出弹簧-插值法，通过减小弹簧法的求解规模来提高网格变形的效率。动态层法[23]则是在非定常计算中使绕各个物体的子网格随物体一起运动，不断建立网格之间插值关系，该方法不需要网格再生和变形，具有处理多体间大幅相对运动的能力。局部网格重构法针对边界位移比单元网格尺寸过大的情况进行网格重构[24]，下文数值模拟中通过应用局部网格重构法和弹簧变形法相结合的方法[25]，成功克服了算例中碎片飞行中因大位移问题而产生的网格质量差、出现负体积、结果不收敛等弊端。

2.3 动网格技术与UDF二次开发

通过编译UDF程序，准确描述了碎片因受内外压强差而产生的动力响应，使碎片运动得以体现，动网格技术则解决了网格的畸变变形，克服了碎片运动的大位移问题。二者的结合使得此工程问题顺利求解，为预测轮胎爆破后碎片获得能量、爆破气流能量等提供了数值参考，具有学术价值和工程实践意义。

3 数值建模

3.1 航空轮胎爆破模型

目前国内外公开文献未见研究轮胎爆破碎片受内外压引发的动力响应相关实验数据，故采用JAA TGM/25/08[8]中给定的碎片模型，标准中规定轮胎大碎片定义厚度为胎面的全厚度，尺寸为W×W，W为轮胎胎面宽度；并根据轮胎实际服役条件进行建模及数值模拟，以便将数值模拟结果与标准中相关规定进行对比分析。仿真分析的轮胎为某型号飞机前轮胎，规格为24×7.7 12PR，仿真轮胎碎片尺寸为0.201 93 m×0.201 93 m(0.040 m2)，厚度为0.020 3 m，质量为0.934 4 kg。进行1∶1建模，如图2所示，采用二维模型网格足够达到计算要求，确定轮胎碎片在x与y方向的大小，z方向的长度数据则在编译的UDF文件中体现，以满足三维尺寸上的一致性。

图2 爆破轮胎及碎片模型Fig.2 Model for bursting tire and debris

3.2 模型选择及参数设置

3.2.1 湍流模型

湍流模型采用Spalart-Allmaras模型，该模型是一种单方程湍流模型，在该方程里不必计算和剪应力层厚度相关的长度尺度。该模型适用于航空领域，主要用于求解墙壁束缚流动(高速可压)，其数值鲁棒性较好[26]，已经显示出很好的效果，本文中除爆破碎片外其余部分均为墙壁，轮胎内部为高压流体，符合此模型适用范围。

其方程为

(4)

式中：u为流动速度；μt为湍流黏性系数；ν为湍流运动黏性系数；σν和Cb2为Spalart-Allmaras模型常数；Gν为湍流黏度生成项；Yν为近壁区域的湍流黏性耗散项。

3.2.2 动网格设定以及UDF二次开发程序设计

动网格用于模拟碎片在空气域中的运动，而动网格由碎片运动方程来控制。碎片运动方程的确定是一个十分复杂的过程，由于碎片所受的力是随时间和空间的变化而变化的，某时刻(假设该时刻碎片已经开始运动)碎片的受力情况如图3所示。根据牛顿第二定律可知：

(5)

式中：m为碎片质量；P1为碎片一侧所受内压；P0为大气压强；A1、A0为碎片两侧的作用面积。

碎片的位置由碎片两侧的流体作用力决定，在Fluent UDF二次开发程序中，将碎片定义为movingwall，其运动过程由软件内提供的DEFINE_CG_MOTION宏函数用C语言将式(5)进行编译，根据读取碎片两侧流场实时变化的流体作用力进行积分获得碎片受到的流体作用力。由于内外压不平衡，碎片便开始产生运动达到新的位置，网格也随之不断更新，如此循环往复，直到满足停止的条件为止。

轮胎碎片的飞行轨迹以及获取初速度的方式是由轮胎碎片两侧的压力差产生的，通过C语言编译的UDF程序来完成轮胎碎片飞行的动力响应；网格更新方法采用弹簧近似光滑模型和局部重划模型。

图3 爆破轮胎碎片受力模型Fig.3 Model for tire bursting debris threat force

3.2.3 基本假设

1) 初始状态时，轮胎本身温度与内部气体温度、大气环境温度相同，均设为300 K。

2) 轮胎外部和轮胎面与周围空气形成对流，取对流热传导系数为恒定值。

3) 认为外部大气环境压力稳定，设为0.1 MPa；轮胎内压稳定。

4) 初始状态模型静止。

5) 碎片变形可忽略，视其为刚体。

3.2.4 流体介质

数值模拟中流体介质为空气，与实际环境中介质完全相同，轮胎中的气体为氮气，因其物性与空气接近暂且统一处理以简便计算，空气性质相关参数如表1所示。

表1 空气热相关参数Table 1 Thermodynamic parameters of air

4 模拟结果与分析

考虑到求解该问题的难收敛性，采用密度基隐式与压力基结合的方法进行求解，求解之前对计算域进行初始化，根据FAA/FAR25.733[27]的规定，每个轮胎最大承载能力应至少比其所在位置应承受的飞机载荷大7%，初始充气内压也要随额定载荷的改变而成比例改变，充气内压在有负荷时工作压力要比无负荷时高出4%。降落时由于重力影响出现的轮胎下沉变形等会直接反映在内部压强的增大上，由于具体数值不能确定，故以该轮胎额定充气压力值1.1 MPa为中心，取范围较大的1.0 MPa、1.1 MPa和1.3 MPa的工况分别进行计算，在此范围内包括了轮胎可能达到的内压谷值与峰值，同时可对比分析内压变化对爆破碎片的动力响应产生的影响。计算采用固定时间步长10-4s，设置每个时间步最多迭代次数为20次。考虑到轮胎内部压力释放过程极为迅速，位移也相对较大，故在碎片飞出计算域时自动停止计算。

4.1 轮胎碎片动力响应

4.1.1 数值计算结果

图4为轮胎碎片分别在内压p=1.0，1.1，1.3 MPa 下发生物理爆破后，速度v迅速上升达到峰值，又随时间下降的变化曲线。

图4为前0.05 s内速度随时间变化曲线，图4 局部放大图为前0.003 s的速度随时间变化曲线，以便清楚表示其速度拐点。从图4局部放大图可以看出碎片快速加速过程在0.003 s内全部完成，瞬时速度达到极值，内压基本释放完毕，对碎片的冲击作用基本完成，此后碎片仅在空气阻力的作用下开始减速运动。

图4 爆破轮胎碎片速度响应曲线Fig.4 Velocity response curves of tire bursting debris

在CS-25修正案中在不考虑内压作用以及胎面厚度的情况下定义轮胎落地的轮胎速度为爆破碎片起始速度，此模型则成功考虑了轮胎内压释放引发的碎片动力响应。

4.1.2 数值结果理论验证

物理爆炸如压力容器破裂时，气体膨胀所释放的能量(即爆破能量)不仅与气体压力和容器的容积有关，而且与介质在容器内的物性相态有关。有的介质以气态存在，如空气、氧气、氢气等，有的以液态存在，如液氨、液氯、高温饱和水等。容积与压力相同而相态不同的介质，在容器破裂时产生的爆破能量也不同，爆炸过程也不完全相同，其能量计算公式也不同。

对于压力容器中介质为压缩气体，即以气态形式存在而发生物理爆炸的情况，其释放的爆破能量为

(6)

式中：Eg为气体爆破能量，kJ；p′为容器内气体的绝对压力，MPa；V′为容器的容积，m3；κ为气体的等熵指数，即气体的定压比热容与定容比热容的比值。

对空气、氮气、氧气、氢气、一氧化碳等常用气体的等熵指数均取为1.4或近似1.4，得到气体的爆破能量为

Eg=CgV′

(7)

式中：Cg为常用压缩气体爆破能量系数，kJ/m3。

各种常用压力下的气体爆破能量系数如表2所示。压力容器爆破时，爆破能量在向外释放过程中以冲击波能量、碎片能量和容器残余变形能量3种形式表现出来，其中后两者所消耗的能量只占总爆破能量的3%～15%，也就是说大部分的能量产生空气冲击波[28]。

现将表2数据用线性插值法确定1.1 MPa以及1.3 MPa的Cg数据，并计算轮胎内部总能量，将数值模拟结果中碎片所获动能及占比列于表3。

以内压1.0 MPa的轮胎为例，根据理论计算得到轮胎内压总能量为62.49 kJ，其碎片的最高速度达到78 m/s，动能约为2.84 kJ，所占比例为4.55%；同理得到内压1.1 MPa与1.3 MPa的结果分别为8.22%与9.87%，该结果满足经验范围的参数，并在一定程度上体现了爆破碎片生成以及飞行过程中的基本规律和特点，随着内压升高，碎片获取能量的比例也随之提高。

表2常用压力下气体爆破能量系数

Table2Energyfactorofgasexplosionunderdifferentpressure

p/MPa0.81.01.62.5Cg/(103kJ·m-3)1.11.42.43.9

表3不同内压下轮胎碎片所获动能及占比

Table3Kineticenergyandpercentageoftiredebrisunderdifferentpressure

p/MPa1.01.11.3Kineticenergy/kJ2.845.658.02Totalenergy/kJ62.4968.7481.24Percentage4.558.229.87

现将内压为1.0 MPa时轮胎爆破碎片在2.5 m 范围内的动能数值列于表4。由表可见，碎片动能在2.5 m范围内，均保持在2 kJ以上，不同位置的碎片动能可为轮胎周围零部件的强度设计提供一定参考。

表4轮胎爆破碎片不同位置动能

Table4Kineticenergyatdifferenttireburstingdebrislocations

Distance/m0.40.81.01.62.5Kineticenergy/kJ2.692.542.482.322.21

4.2 流场云图

流场中气体膨胀的过程可以通过流场的压力云图、速度云图进行清晰地表达。流场发展的具体阶段主要由内外压力平衡进度来界定。爆破过程流场发展类似，仅以内压为1.0 MPa情况为例进行说明。图5为轮胎在爆破发生后的流场压力云图(图中标尺为绝压，单位为Pa)。图5(a)～图5(c)中，气体初步膨胀，内部气体出口压力在0.002 s内迅速从绝压1.0 MPa下降到0.5 MPa。图5(d)中，气体进一步膨胀，内部气体总体压力在0.003 s内迅速将至0.1 MPa，内外压力平衡速度加快并基本达到平衡，这说明气体在0.003 s时已充分膨胀，与碎片速度于0.003 s时获得最大速度的分析结果对应，此后流场与轮胎碎片状态的变化则基本是在惯性作用下产生的。

图6为轮胎在爆破发生后的流场速度云图发展过程(标尺单位为m/s)。图6(a)中，0.000 1 s时流场初步膨胀，流动速度较大的气体都集中在轮胎碎片与轮胎的间隙；图6(b)～图6(c)中，气体进一步膨胀，且流动速度仍维持在较大值，最大流动速度为508.1 m/s；由0.002 s开始气流速度发生缩减，直到t=0.01 s，如图6(f)所示，流场的膨胀基本结束，流场最大速度值衰减至89.7 m/s，此时碎片飞行速度也达到70 m/s，气流的冲击影响已经不再显著。综合压力云图可以看出，压力降最明显处就是气体膨胀速度最大处(即模型预设缺陷的缺口处)。

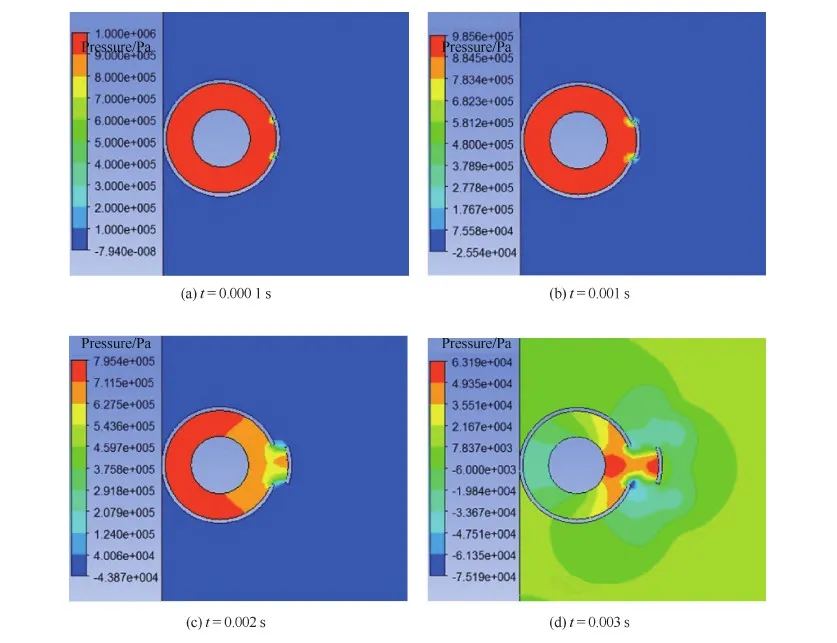
图5 爆破轮胎流场压力云图Fig.5 Pressure contour of tire bursting flow field

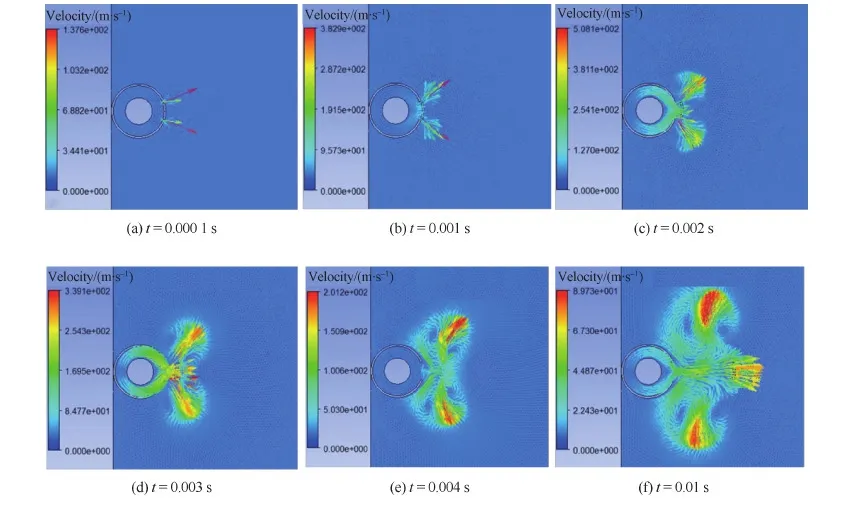
图6 爆破轮胎流场速度云图Fig.6 Velocity contour of tire bursting flow field

4.3 与数学模型结果对比

白杰等[9]在外来物损伤条件下利用压力容器爆炸模型建立轮胎碎片计算数学模型，得到碎片的抛射速度公式为

(8)

式中：a为初始裂纹长度；l为初始裂纹宽度；M为碎片的质量。

现将数值模拟中内压为1.0，1.1，1.3 MPa的初始条件代入式(8)，得到其碎片抛射速度，根据文献[9]所述，其抛射速度的定义为碎片离开轮胎瞬间的速度，为增加可比性，与数值模拟碎片离开初始位置时的速度(即碎片位移刚好达到轮胎胎面厚度时的速度)进行对比，见表5。

表5两种模型不同内压下轮胎碎片速度

Table5Velocityoftiredebrisunderdifferentpressureandmodels

p/MPaVelocity/(m·s-1)MathematicalmodelNumericalsimulation1.033.1836.281.134.8137.411.337.8442.31

由表5中可看出，数值仿真与数学模型在相同条件下所获速度值结果契合度很高，但仍然存在高于数学模型10%左右的误差。主要原因是：① 数学模型考虑了碎片分离过程的裂纹扩展过程，即胎面脱离过程中所消耗的能量，故其速度值比数值模拟结果偏低；② 数值模拟充分考虑了整个内压释放到与外界气压达到平衡的过程，而不仅仅是脱离瞬间的状态，气压的平衡过程并非是在碎片脱离轮胎瞬间完成的，在碎片脱离轮胎瞬间仍会受到未平衡的压强作用，并且随着初始内压的增大气压平衡的时间会有所增大，碎片获取的速度也会随之增大，故数值模拟的结果相比数学模型更为全面、准确。

5 结 论

1) 航空轮胎爆破失效后轮胎碎片动力响应表现为典型的流固耦合问题；利用Fluent中动网格和UDF技术相结合的方法顺利对其完成数值模拟，提高了模拟的真实性，对其他运动流场的数值模拟具有重要的借鉴意义。根据分析，认为轮胎爆破失效是轮胎先前的缺陷造成的，将碎片受冲击后的动态过程分为内压释放冲击加速和以一定初速度在空气阻力下减速运动两个阶段。

2) 爆破后碎片的物理加速完成迅速，在模拟情况下于0.003 s内达到最大速度，内部压缩气体在0.01 s内与外部大气的压力完成平衡。

3) 轮胎碎片所获取能量占总能量比例随着内压增大而增大，且内压对碎片造成的冲击作用明显，在航空适航标准相关条款中是不可忽略的。

4) 轮胎爆破后，最明显压力降与最大气体流动速度出现在同一区域。

通过数值模拟与数学模型对比，弥补了数学模型考虑内压释放时间过短，未考虑内压释放到平衡过程的缺点。

[1] 龚荣亮. 飞机轮胎的结构及常见故障探究[J]. 中国高新技术企业, 2011(27): 81-82.

GONG R L. Aircrafttire structure and common faults[J]. China High Technology Enterprises, 2011(27): 81-82 (in Chinese).

[2] 张建敏. 飞机轮胎爆破模式浅析[J]. 力学季刊, 2014, 35(1): 139-148.

ZHANG J M. A brief study on damaging effects of aeroplane tire and wheel failures[J]. Chinese Quarterly of Mechanics, 2014, 35(1):139-148 (in Chinese).

[3] 周易之, 舒平. 起飞阶段冲偏出跑道事故预防分析[J]. 中国安全科学学报, 2009, 19(1): 38-44.

ZHOU Y Z, SHU P. Analysis on prevention of runway overrun/excursion accident during takeoff[J]. China Safety Science Journal, 2009, 19(1):38-44 (in Chinese).

[4] 周应求. 航空轮胎爆破的原因分析及其预防措施[J]. 化工新型材料, 1980(10): 1-6.

ZHOU Y Q. Analysis and preventive measures of aviation tire blasting[J]. New Chemical Materials, 1980(10):1-6 (in Chinese).

[5] 霍志勤, 罗帆. 近十年中国民航事故及事故征候的统计分析[J]. 中国安全科学学报, 2006, 16(12): 65-71.

HUO Z Q, LUO F. Statistic analysis on accidents and incidents in the last decade in China civil aviation[J]. Chinese Safety Science Journal, 2006, 16(12): 65-71 (in Chinese).

[6] HEFNY A F, EID H O, AL-BASHIR M, et al. Blast injuries of large tyres: Case series[J]. International Journal of Surgery, 2010, 8(2): 151-154.

[7] European Aviation Safety Agency. Notice of proposed amendment (NPA) 2013-02, Protection from debrisimpacts[S]. 2013.

[8] Joint Aviation Authorities. JAA temporary guidance material, TGM/25/08 (issue2), Wheel and tire failuremodel[S]. 2002.

[9] 白杰， 董兴普， 王伟. 外来物损伤条件下航空轮胎爆破碎片产生机理及速度分析[J]. 橡胶工业, 2011, 58(11): 658-661.

BAI J, DONG X P, WANG W. Formation mechanism and speed of aircraft tire burst debris under FOD[J]. China Rubber Industry, 2011, 58(11): 658-661 (in Chinese).

[10] 黄喜平， 陆波， 曹丹青. 在飞机起落架轮胎爆破时主起落架系统安全性分析方法[J]. 流体传动与控制, 2013(5): 22-24.

HUANG X P, LU B, CAO D Q. Method of main landing gear system security analysis when airplane landing gear’s tire is bursting[J]. Fluid Power Transmission and Control, 2013(5): 22-24 (in Chinese).

[11] 谢孟恺， 周昌明， 范平. 轮胎爆破下飞机液压能源系统安全性分析方法[J]. 航空科学技术, 2015, 26(9): 46-49.

XIE M K, ZHOU C M, FAN P. Aircraft hydraulic system safety analysis method for tire burst[J]. Aeronautical Science and Technology, 2015, 26(9): 46-49 (in Chinese).

[12] 李田. 高速列车流固耦合计算方法及动力学性能研究[D]. 成都: 西南交通大学, 2012.

LI T. Approaches and dynamic performances of high-speed train fluid-structure[D]. Chengdu: Southwest Jiaotong University, 2012 (in Chinese).

[13] 邢景棠， 周盛， 崔尔杰. 流固耦合力学概述[J]. 力学进展, 1997, 27(1): 20-39.

XING J T, ZHOU S, CUI E J. A survey on the fluid-solid interaction mechanics[J]. Advances in Mechanics, 1997, 27(1): 20-39 (in Chinese).

[14] STEIN K, TEZDUYAR T E, BENNEY R. Automatic mesh update with the solid-extension mesh moving technique[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(21-22): 2019-2032.

[15] 陈锋, 王春江, 周岱. 流固耦合理论与算法评述[J]. 空间结构, 2012, 18(4): 55-63.

CHEN F, WANG C J, ZHOU D. Review of theory and numerical methods of fluid-structure interaction[J]. Spatial Structures, 2012,18(4): 55-63 (in Chinese).

[16] WALL W A, GERSTENBERGER A, GAMNITZER P, et al. Large deformation fluid-structure interaction—Advances in ALE methods and new fixed grid approaches[C]//Lecture Notes in Computational Science and Engineering, 2006, 53: 195-232.

[17] 何涛. 流固耦合新算法研究及其气动弹性应用[D]. 上海: 上海交通大学, 2013.

HE T. Novelpartitioned coupling algorithms for fluid-structure interaction with applications to aero elasticity[D]. Shanghai: Shanghai Jiao Tong University, 2013 (in Chinese).

[18] 刘学强, 李青, 柴建忠, 等. 一种新的动网格方法及其应用[J]. 航空学报, 2008, 29(4): 817-822.

LIU X Q, LI Q, CHAI J Z, et al. A new dynamic grid algrithm and its application[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(4): 817-822 (in Chinese).

[19] MURMAN S M, AFTOSMIS M J, BERGER M J. Implicit approaches for moving boundaries in a 3-D Cartesian method: AIAA-2003-1119[R]. Reston, VA: AIAA, 2003.

[20] LIEFVENDAHL M, TROENG C. Deformation and regeneration of the computational grid for CFD with moving boundaries: AIAA-2007-1458[R]. Reston, VA: AIAA, 2007.

[21] HASSAN O, MORGAN K, WEATHERILL N. Unstructured mesh methods for the solution of the unsteady compressible flow equations with moving boundary components[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007, 365(1859): 2531-2552.

[22] 周璇， 李水乡， 陈斌. 非结构动网格生成的弹簧-插值联合方法[J]. 航空学报, 2010, 31(7): 1389-1395.

ZHOU X, LI S X, CHEN B. Spring-interpolation approach for generating unstructured dynamic meshes[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1389-1395 (in Chinese).

[23] FAST P, SHELLEY M J. A moving overset grid method for interface dynamics applied to non-Newtonian Hele-Shaw flow[J]. Journal of Computational Physics, 2004, 195(1): 117-142.

[24] 辛颖. Fluent UDF方法在数值波浪水槽中的应用研究[D]. 大连: 大连理工大学, 2013.

XIN Y. Applicationof fluent UDF method in the study of numerical wave tank[D]. Dalian: Dalian University of Technology, 2013 (in Chinese).

[25] 伍贻兆， 田书玲， 夏健. 基于非结构动网格的非定常流数值模拟方法[J]. 航空学报, 2011, 32(1): 15-26.

WU Y Z, TIAN S L, XIA J. Unstructured grid methods for unsteady flow simulation[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1): 15-26 (in Chinese).

[26] 杨小权， 杨爱明， 孙刚. 一种强耦合Spalart-Allmaras湍流模型的RANS方程的高效数值计算方法[J]. 航空学报, 2013, 34(9): 2007-2018.

YANG X Q, YANG A M, SUN G. An efficient numerical for coupling the RANS equations with Spalart-Allmaras turbulence model equation[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2007-2018 (in Chinese).

[27] USA Federal Aviation Administration. FARS, PART25- airworthiness standards: Transport category airplanes[S]. 2000.

[28] 赵雪娥， 孟亦飞， 刘秀玉. 燃烧与爆炸理论[M]. 北京: 化学工业出版社, 2011: 194.

ZHAO X E, MENG Y F, LIU X Y. Combustion and explosion theory[M]. Beijing: Chemical Industry Press, 2011: 194 (in Chinese).

(责任编辑： 李明敏)

*Correspondingauthor.E-mail:malizjut@zjut.edu.cn

Dynamicresponseofaircrafttireburstingdebrisunderinternalpressure

ZHANGFan1,ZHENGJinyang1,MALi2,*

1.CollegeofEnergyEngineering,ZhejiangUniversity,Hangzhou310012,China2.InstituteofAppliedMechanics,ZhejiangUniversityofTechnology,Hangzhou310012,China

Whentheaircrafttirebursts,thevelocityofthedebriswillbesignificantlyincreasedbecauseoftheimpactofinternalpressure，ratherthanremainconsistentwiththatofthetireinlandingasspecifiedbyairworthinessstandards.ThemodelfordynamicresponseofburstingdebrisunderinternalpressurereleasingissimulatedbyusingdynamicgridanduserdefinedfunctioninFluent,andthedynamicresponseprogramiscodedbyusingtheuserdefinedfunction.Tireburstingfailureisassumedtobecausedbypreviousdefectsofthetire,andthedynamicprocessofdebriscanbedecomposedintotwophasesaccelerationphaseundertheimpactofinternalpressurereleasing,anddecelerationmotionphaseunderairresistance.Thereal-timepressuredifferencebetweenbothsidesofdebrisisregardedastheonlypowersourceofthesimplifiedphysicalburstmodelforanalysisofthevelocityofdebris,theflowfieldpressureandvelocitychangesaffectedbyinternalpressure.Thereductionmodelmakesupthedeficiencythatpreviousmathematicalmodelsdonottakeintoaccountthebalanceofinternalandexternalpressure.Themodelcanprovidenumericalreferenceforpredictingtheenergyofdebrisafterburstingandtheenergyofburstingairflow,andcanthushelpwiththeproposalofcorrespondingsafetyprecautions.

aircrafttire;burstingdebris;fluid-solidcoupling;CFD;userdefinedfunction

2016-12-06；Revised2017-02-13；Accepted2017-03-03；Publishedonline2017-03-131638

URL：www.cnki.net/kcms/detail/11.1929.V.20170313.1638.002.html

s：TheNationalKeyResearchandDevelopmentProgramofChina(2016YFC0801501);CooperationProjectwithAviationIndustryCorporationofChina

2016-12-06；退修日期2017-02-13；录用日期2017-03-03； < class="emphasis_bold">网络出版时间

时间：2017-03-131638

www.cnki.net/kcms/detail/11.1929.V.20170313.1638.002.html

国家科技支撑计划 (2016YFC0801501)； 中航工业合作项目

.E-mailmalizjut@zjut.edu.cn

张帆， 郑津洋， 马利． 内压作用下的航空轮胎爆破碎片动力响应J． 航空学报,2017,38(8):221032.ZHANGF,ZHENGJY,MAL.DynamicresponseofaircrafttireburstingdebrisunderinternalpressureJ.ActaAeronauticaetAstronauticaSinica,2017,38(8):221032.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221032

V19

A

1000-6893(2017)08-221032-10