石油价格与股票市场的动态相关性分析

郦 博 文，巴 曙 松,2，韦 伟

(1.中国科学技术大学 管理学院，安徽 合肥 230026; 2.中国银行业协会，北京 100033； 3.上海证券交易所，上海 200120)

石油价格与股票市场的动态相关性分析

郦 博 文1，巴 曙 松1,2，韦 伟3

(1.中国科学技术大学 管理学院，安徽 合肥 230026; 2.中国银行业协会，北京 100033； 3.上海证券交易所，上海 200120)

能源信息变量和金融信息变量的关系是能源经济学的重要课题。文章试图应用非参数时变Copula方法来检验石油价格与股票市场间的相关关系，发现石油价格和全球股票市场间的相关性随着时间变化而发生变化。通过度量尾部相依系数的变化趋势，两者之间的相关性在经济动荡或金融危机期间显著增强。

石油价格；股票市场；时变Copula；非参数方法；尾部相关性

一、引 言

随着全球经济的高速发展以及工业化进程不断深入，能源市场和金融市场的联系越来越密切，能源经济学成为了重要的研究课题。石油作为一种战略资源，近年来成为规避通货膨胀和美元疲软风险的“黑黄金”，各国对石油的需求也不断攀升。石油成为名符其实的“经济血液”，其价格直接反映一个国家的经济变动状况与趋势。在经济金融领域，股票素有市场经济发展的“晴雨表”之称，即在市场有效的前提下，股市发挥着市场经济预测的功能。股票价格也是经济金融研究中重要的信息变量。所以，石油价格与股票市场之间应存在密切的关联性。

目前，学术界关于油价变化对股票市场的影响，并没有得出一致的结论。Apergis和Miller使用8个发展中国家作为研究样本，得出石油价格变动对于股票市场并没有显著影响[1]。相反，Park和Ratti以美国与13个欧洲国家为样本，结果显示石油价格的波动对股票的收益率有显著的影响，且对于石油进口国和石油出口国的影响有所不同[2]。Cong和Wei使用VAR模型分析石油价格对中国股市的影响，发现其影响并不十分显著[3]。Miller和Ratti利用VECM模型对石油价格和股票市场之间的长期相关性进行研究，得出在不同时期石油价格和股票之间相关性的大小是不同的结论[4]。Reboredo和Ugolini等应用分位点回归方法研究石油和股票市场相关性，发现在金融危机期间的相关性更加显著[5]。国内学者也做过相关研究，金洪飞和金荦采用VAR-GARCH模型研究发现中国股票市场与国际石油价格之间不存在相关关系[6]。孙晨辉和李富有应用Logistic模型也进行了相关研究[7]。李素芳和朱慧明应用石油与股市之间的非对称效应，指出石油和研究对象中的各国股市存在着格兰杰因果关系[8]。但是正是运用这些研究方法，他们往往假设资产收益率服从正态分布，那么这些方法就存在着不可避免的局限性。而金融数据往往是非线性的，具有非对称相依关系，存在着尖峰厚尾、时变偏斜和波动聚类等特点。此外，他们也无法捕捉到数据的非线性相关性或尾部收益率曲线的变化。

与上述的方法比较，Copula方法更为适合研究二者之间的动态相关性。Copula函数既不要求资产收益是否符合正态分布这个前提假设条件，也不拘泥于联合分布函数是否符合椭圆分布，可以建立一个更有效的联合分布。Schweizer和Sklar提出了Copula函数方法[9]，Embreehts和McNeil较早地将Copula理论应用到金融数据的分析上[10]。Riadh等运用Copula-GARCH的方法研究石油和汇率间的相关关系[11]。但这些Copula方法都基于常系数方法，假定相依结构不随时间变化而发生变化[11]。Patton最先研究时变Copula模型，使用条件Copula对研究汇率之间的相关性建模，并发现它们的相关性是随时间变化且呈现非对称的[12]。Chen和Fan提出半参数Copula函数理论，使用经验分布代替假设的边缘分布以减少估计计算产生的误差[13]。Riadh等使用时变Copula来测量石油价格冲击对东欧六国的影响[14]。以上研究主要是检测相关系数是否逐渐增大，依此来说明两个市场之间的关系，忽视对相关程度以及变化趋势的分析。

还有一些研究引入时变Copula方法，通常假设参数演变方程或固定数据窗口，但金融市场之间的相依结构具有相当的不确定性以及复杂性，因此，估计时变系数时会带来较大的偏差。Hafner和Reznikova提出用非参数时变Copula方法来研究石油市场与股票市场之间的动态相关性和变化趋势[15]。龚金国和时代敏进一步给出了非参数时变Copula模型的非参数估计算法[16]。这些偿试给本研究提供了借鉴和启示。本文应用非参数时变Copula方法，研究了布伦特原油FOB现货价格与全球6个股票市场的相关关系，发现原油价格和股指的收益率间的尾部相关系数随着时间变化而变化，在经济动荡时期或金融危机期间，其相关性显著增强。研究能源信息变量和金融信息变量的关系，有利于规避能源金融风险，帮助投资者优化全球资产配置，提高风险管理水平。

二、理论方法

1.Copula函数与Sklar定理

Copula函数也称连接函数，是利用边缘分布来确定其联合分布的数学方法，可用来描述随机变量的非线性关系以及度量随机变量之间的相关程度和相依机制。

定理1(Sklar定理)：设随机向量(X1,…,Xp)的联合分布函数为具有边缘分布F1,…,Fp的联合分布，则存在CouplaC：[0,1]p→[0,1],使得对所有随机变量Xi，满足F(X1,…,Xp)=C(F1(x1),…,Fp(xp))。

2.时变Copula函数

假定随机变量(X,Y)的联合分布函数为H(x,y)，其边缘分布分别是F(x)和G(x)，样本观察值为(xt,yt)。根据Sklar定理，那么有H(x,y)=C(F(x),G(y))成立，其联合密度函数为H(x,y)=C12[F(x),G(y)]f(x)g(x)。

作为一种重要的阿基米德Copula函数，Gumbel Copula能够准确地描述收益率之间的相依结构。二元Gumbel Copula的函数形式如(1)所示：

(1)

3.时变Copula的非参数估计

本文采用非参数建模方法对时变Copula函数的参数进行估计。我们直接将时变参数看作时间t的一个非参数函数，这样就不需要对时变尾部相关系数做出任何假设，避免了演化方程中的繁琐计算，从而达到对时变Copula模型的时变参数进行建模的目的。文中我们直接采用经验分布函数将(xi,yi)转化为(F(xi),G(yi))来对Copula参数进行估计。假设Copula的参数α是时间的函数，且至少二阶可导，α(t)是时间t的线性函数。因此，局部似然函数就可以表示为：

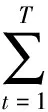
(2)

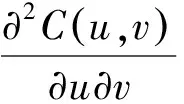
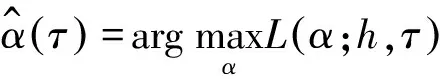
(3)

4.光滑参数h的选择

在非参数的估计过程中，光滑参数h的选择是非常重要的，光滑参数的选择直接关系到参数估计的确定性与稳定性。在通常情况下，利用核函数时都应用最小积分均方误差(MISE)来确定最优窗宽，而由于本文所研究的局部极大似然估计中此方法不能得出确切结果，因此，我们采用的龚金国等所给出最大似然函数法[13]。给定光滑参数h的取值集合Ωh，然后使每一个集合点hi且hi∈Ωh，在样本观测值的经验分布函数(F(xi),G(xi))条件下根据(3)式计算时变参数α(τ,hi)得到hi时对数似然函数值：

(4)

因此，每一个可能的hi都得到了相应的L(hi)，那么找到最优的窗hopt方法，可以通过极大化(4)式所得到，即：

(5)

5.尾部相关系数

尾部相关系数是Copula理论当中的重要内容，它表示一个观测变量出现极值情况下，另一个变量也出现极值的概率。尾部相关系数可以较好地测度极端事件发生时金融市场的关联性。

定义2(上尾和下尾相依)：设随机变量X和Y的分布分别为F和G，

(6)

若(6)存在，λu称为X和Y的上尾相依系数。若λu∈[0,1]，称X和Y上尾渐相依；若λu=0，称X和Y上尾渐近独立。类似的，

(7)

若(7)存在，则称λl为X和Y的上尾相依系数。

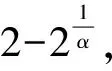
三 、数据描述

本文选用布伦特原油FOB现货价格(Brent Spot Price FOB)代表国际石油价格。这是因为与国际WTI原油价格相比，全球有超过60%的石油贸易是参照布伦特原油进行定价的，且布伦特原油的供应相对稳定，受当地影响因素极小。为了尽可能全面反映股市的波动情况，本文选取全球6个具有代表性的国家(或地区)的股票价格指数，分别为：美国S&P500指数、沪深300指数、日经指数、KOSPI指数、FTSE100指数、沪深300指数和DAX指数，以此分别代表美国、中国、日本、韩国、英国和德国的股票市场状况。考虑到2008年美国次贷危机引发的全球金融危机和后续发生的欧债危机，本文选取样本的区间为2006年1月1日至2016年1月1日，包括了石油价格及股票指数的大幅动荡期。采用各股指的对数收益率反映股价变化，计算方法为：Rt=ln(pt)-ln(pt-1)。其中，Rt表示指数对数收益率，pt表示t时期的市场指数。由于不同国家在节假日上的差异，剔除了交易日不匹配的数据，以得到在时间上一致的序列数据。

表1显示了石油价格和各国指数对数收益率的描述性统计量。可知，除日本外，石油价格和各国股指序列的平均收益率序列都是呈正的，均值都非常接近于0。标准差反映着收益率序列的离散程度，都在1.5左右。S&P500指数、沪深300指数、日经225指数、KOSPI指数、FTSE100指数和DAX指数的偏度系数明显小于0，表明它们的收益率都是左偏的。另外，所有的股指收益率的峰度系数都不显著为0，可见收益率序列都呈尖峰厚尾的特征，收益率序列不能很好地由正态分布拟合。J-B统计量也在至少99%的置信水平上拒绝了序列为正态分布的假设。

表1 Brent价格与各国指数对数收益率描述性统计

注：石油价格和各国股指数据均来源于Wind数据库，使用R软件数据处理，下同。

四、实证分析

1.Copula函数的拟合

本节使用Gumbel Copula函数模型拟合布伦特原油价格与各国股指收益率。Gumbel Copula并不要求收益率序列具有对称的上下尾相依结构，它能够准确地描述上尾相依结构，且其参数与尾部相关系数具有对应的函数关系，因而更适合对尾部相关结构的建模。经过实证结果发现，收益率之间的相依结构可以被Gumbel Copula很好地拟合，拟合效果优胜于其他阿基米德Copula类。在许多研究中也都被证实Gumbel Copula能够最好地用来拟合收益率之间的相依结构。之后对Copula拟合优度进行了检验，具体结果见表2。

表2 Brent价格与各国指数收益率Gumbel Copula拟合结果

2.拟合结果分析

在此，将使用式(2)、(3)给出的局部极大似然估计方法来对布伦特原油价格与各国指数收益率之间的时变Copula参数进行估计。由于过于精细的时间刻度τ没有实际经济意义，所以本文基于每个交易日计算一个Copula参数值，这样也可以近似将Copula参数看作是关于时间的平滑函数。估计时需要选择适合的窗宽hopt，通过程序计算最优窗宽为100个交易日。在计算出每个时间点的Gumbel Copula参数值α(τ)后，计算出每个交易日的上尾相依系数λ(u)(t)。本文将此时间区间内尾部相关系数的平均值大小作为衡量相关性大小的方法。根据度量上尾相依系数λ(u)(t)的大小及变化趋势来进行石油价格和股票市场的相关性分析。因为Gumbel Copula度量的是上尾相关系数，所以将对数收益率取负号进行建模，从而可以研究股票指数收益率的下尾相关系数的变化。

图1 各国指数与Brent原油收益率之间尾部相关系数

图1显示了使用Gumbel Copula模型拟合的布伦特原油价格与各指数收益率之间的尾部相关系数的变化趋势。可以看到，石油价格和指数之间的尾部相关系数是随着时间变化而变化的，且石油与各国指数间的Copula尾部相关系数的变化具有相似的特征。在2007年7月次贷危机爆发之前，原油价格与各国指数收益率尾部相关系数都在0.1左右，这表明在金融危机发生之前二者之间的尾部相依程度很弱，可以认为两者间几乎没有相关性。随着金融危机的蔓延，全球经济的持续下滑抑制了经济的增长，也减少了潜在的和现有的消费者对石油的需求。经济基本面的危机也导致原油生产资金方面的压力，随之原油价格短时间内急剧下跌。在2008年9月15日，美国第五大投资银行雷曼兄弟公司陷入严重财务危机并宣布申请破产，由此标志着次贷危机达到了最高潮。次贷危机发生后，石油价格和各国股指收益率间的尾部相关系数急剧增加，并且相对于之前的时间都到达了一个高点。例如，原油价格和美国标普500指数的尾部相关系数增长显著，从0上升到了0.5，之后保持在了一个相对较高的水平；原油价格和沪深300指数的尾部相关系数也从0上升至0.25。从图1可以看出，石油价格和美国标普500指数的尾部相依系数增长幅度最大，而亚洲国家股指的上尾相依系数增长幅度相对较小，石油价格与其他欧洲国家股指间的尾部相关系数涨幅则介于美国标普500指数与沪深300指数之间。随着次贷危机影响的逐渐消退，世界经济面逐渐向好，石油和各国股指的收益率间尾部相关系数都有着一定幅度的下降，但随着2012年欧债危机逐渐激化，上尾相关系数又逐渐增加形成一个新的峰值，并且这样的趋势在美国、英国、德国指数的走势图中显示的更加明显。在2014年最后一季度至2016年，石油价格持续下跌，从100美元跌至40美元，幅度较大。2015年6月开始，中国股市发生了持续性暴跌的股灾，进而影响了全球股市。在此期间，石油价格与各国股指间的尾部相关系数也迅速增加，但整体增长幅度小于金融危机期间的增幅。

这也与实际情况相一致，金融危机对美国的经济影响最大，欧洲的国家影响次之，亚洲国家特别是中国所受影响相对最小。IEA(国际能源机构)认为，2009年世界石油价格是对需求预期的响应，无论作为生产者、消费者，还是经营者都在寻找世界经济何时恢复，将以什么样的形态恢复，以及对石油的需求会如何上涨。金融危机爆发之后的2009年，布伦特石油价格从1月的每桶45美元上升至12月的每桶78美元，原油价格的上涨，带来了一些经济复苏的明确信号。之后随着次贷危机影响的减弱和经济的复苏，原油价格和股指收益率之间的尾部相关系数有下降的趋势，甚至一些国家出现了不小幅度的回落。以2009年10月19日三大评级公司下调对希腊的主权债务评级为标志，欧债危机呈逐渐蔓延之势。随着欧债危机的爆发，石油价格和指数的收益率之间的尾部相关系数也再度上升至前期高点，几乎超越次贷危机时期水平且在2010年达到了一个新的高度。之后的一段时间内，原油价格和股指的收益率的上尾相依系数起起伏伏，总体呈下降趋势。这可以解释为，欧债危机对石油市场和金融市场的冲击是长期性的，影响至今也未完全消除。总体来说，原油价格和股指的收益率尾部相关系数是随着时间变化而变化的，并且随着全球金融危机蔓延，它们会持续增长，这说明它们在经济动荡时期收益率相关性更强。

五、结 论

从上述实证结果可以看出本文运用的方法是比较有效的，应用非参数时变Copula方法并且以时变尾部系数作为相关性大小变化趋势的度量方法，很好地捕捉到了原油和股指的收益率间的非线性和非对称关系。现有的很多文献均研究了石油价格与股票市场的相关关系，但它们往往局限于相依结构是静态常系数或者是线性的，从而导致对市场相依结构的测度结果存在着或多或少的偏差。

实证分析结果显示，原油价格和股指的收益率尾部相关系数随着时间变化而变化，并且在经济动荡时期或危机期间相关性显著增强。升高的尾部相关系数也表明，石油价格和股指收益率同时出现负收益的概率在危机期间也会显著增加。此外，在两次金融危机期间石油市场和股票市场间还存在着Forbes和Rigobon所定义的传染效应[17]，这也与Wen的实证研究结果相符合[15]。与次贷危机期间相比，石油和股票市场间的传染效应在欧债危机期间有所增强，并呈现长期化和复杂化的特征。通过研究危机期间石油和金融市场间的尾部相关系数，可以度量它们之间的相关程度及变化趋势。在能源经济学的研究中，研究能源信息变量与金融信息变量之间的关系是促进两大产业共同发展的前提，此举有助于对市场做出预测，并有效地规避潜在的金融风险。通过研究金融危机期间石油和金融市场间的尾部相关系数，可以度量它们之间的相关程度及变化趋势。这可以帮助投资者关注到不同市场间的联动风险，重视投资的风险管理，优化投资组合投资，并且也会得出一些有益于监管层的政策建议。对投资者而言，一是传染效应的存在意味着石油和金融多元化的相关投资组合利益将减少；二是忽略时变的尾部相关性可能导致对投资风险的低估。对监管层而言，一是监管机构应减缓金融化进程的步骤，减少不良波动溢出效应的出现；二是石油进口国应合理地进行石油储存，减少对石油进口的过度依赖，并注重采用创新节能技术。本文通过应用非参数时变Copula的尾部相关系数对石油价格与股票市场的相关性进行研究，但这方面目前所做的工作还是远远不够的，样本的选取还应该更多，且应该偿试使用多种度量方法进行比较研究，在今后的研究中会加以改进与提升。

[1] APERGIS N，MILLER S M.Do structural oil-market shocks affect stock prices?[J].Energy Economics，2009，31(4)：569-575.

[2] PARK J，RATTI R A.Oil price shocks and stock markets in the US and 13 European countries[J].Energy Economics，2008，30(5)：2587-2608.

[3] CONG R G，WEI Y M，JIAO J L，etal.Relationships between oil price shocks and stock market：an empirical analysis from China[J].Energy Policy，2008，36(9)：3544-3553.

[4] MILLER J I，RATTI R A.Crude oil and stock markets：stability，instability，and bubbles[J].Energy Economics，2009，31(4)：559-568.

[5] REBOREDO J C，UGOLINI A.Quantile dependence of oil price movements and stock returns[J].Energy Economics，2016，54(5)：33-49.

[6] 金洪飞，金荦.石油价格与股票市场的溢出效应——基于中美数据的比较分析[J].金融研究，2008,30(2):83-97.

[7] 孙晨辉，李富有.民间金融与正规金融的比较优势与均衡发展——基于 Logistic模型的研究[J].大连理工大学学报(社会科学版)，2014，(1):81-85.

[8] 李素芳，朱慧明，李荣.基于贝叶斯机制转换协整模型的石油——股市非对称效应研究[J].中国管理科学，2015，23(9):46-54.

[9] SCHWEIZER B，SKLAR A.Probabilistic Metric Spaces[M].New York：Courier Corporation，2011.

[10] EMBRECHTS P,MCNEILA,STRAUMANN D.Correlation and Dependence in Risk Management：Properties and Pitfalls[A].DEMPSTERA H.Risk Management Value at Risk & Beyond[C].New York：Cambridge University Press，2001:176-223.

[12] PATTON A J.Modelling asymmetric exchange rate dependence[J].International Economic Review，2006，47(2):527-556.

[13] CHEN X，FAN Y.Estimation and model selection of semiparametric copula-based multivariate dynamic models under copulamisspecification[J].Journal of Econometrics，2006，135(1):125-154.

[14] ALOUI R，HAMMOUDEH S，NGUYEN D K.A time-varying copula approach to oil and stock market dependence：the case of transition economies[J].Energy Economics，2013，39(12):208-221.

[15] HAFNER C M，REZNIKOVA O.Efficient estimation of a semiparametric dynamic copula model[J].Computational Statistics & Data Analysis，2010，54(11):2609-2627.

[16] 龚金国，史代敏.时变 Copula 模型的非参数推断[J].数量经济技术经济研究，2011，28(7)：137-150.

[17] FORBES K J，RIGOBON R.No contagion，only interdependence：measuring stock market comovements[J].The journal of Finance，2002，57(5):2223-2261.

AnalysisoftheDynamicCorrelationbetweenCrudeOilandStockMarkets

LIBowen1，BAShusong1,2，WEIWei3

(1.SchoolofManagement，UniversityofScienceandTechnologyofChina，Hefei230026，China；2.ChinaBankingAssociation，Beijing100033，China；3.ShanghaiStockExchange，Shanghai200120，China)

The correlation between energy variables and financial variables is a key issue in energy economics.In this paper,we employ the non-parametric Time-varying Copula approach to investigate the dynamic between the Brent crude oil price and stock markets,and have found the relationship between oil and stock markets is time-varying.By measuring the tail dependence coefficient,its increase shows that the dynamic relation between the two variables became strong in the economic turmoil and financial crisis.The empirical results have important implications for portfolio diversification and risk management.

Oil price； Stock market； Time-varying Copula； Non-parametric method； Tail dependence

10.19525/j.issn1008-407x.2017.04.006

F830.9

A

1008-407X(2017)04-0040-06

2016-03-10;

2016-05-22

国家自然科学基金重点项目：“复杂纵向数据的统计推断”(11231010)

郦博文(1992-)男，陕西西安人，中国科学技术大学管理学院博士研究生，主要从事金融风险管理与非参数统计研究，E-mail：leefeng92@163.com；巴曙松(1969-)，男，湖北新洲人，教授，博士生导师，主要从事金融机构风险监管研究；韦伟(1989-)，男，安徽合肥人，硕士，研究方向为金融工程。