考虑海底接触的钢悬链式立管静力学行为
, , , ,
(西南石油大学 油气藏地质及开发工程国家重点试验室, 成都 610500)
考虑海底接触的钢悬链式立管静力学行为
陈祥,王小梅,高云,苌北,程俊霖
(西南石油大学油气藏地质及开发工程国家重点试验室,成都610500)
基于考虑海底接触的钢悬链式立管(Steel Catenary Riser, SCR)的结构特性,采用考虑管土分离的线性截断模型对p-y曲线进行描述。通过在立管顶端施加固定的水平位移模拟上端浮体的水平漂移,分别研究立管外径、立管壁厚、管内流体介质以及海流流速的变化对立管位移响应以及等效应力的影响。分析结果表明:立管位移响应随着壁厚和内部流体密度的增加呈下降趋势,随着海流流速的增加呈上升趋势,但外径变化对立管位移响应的影响却不显著。触地点处的等效应力发生了剧烈变化,从触地点到悬挂点,立管所受等效应力呈振荡波形,峰值整体呈上升趋势,波峰之间的间距逐渐增大。立管位移响应主要受立管壁厚、内部流体密度以及海流流速的影响,而立管等效应力主要受立管内部流体密度和海流流速的影响。
钢悬链式立管;海底接触;位移响应;等效应力
0 引 言
钢悬链式立管(Steel Catenary Riser, SCR)是近些年来迅速发展起来的一种新型立管,与张紧式立管(Top Tension Riser, TTR)相比,SCR不需要张紧力补偿,且允许上端浮体在较大范围内运动。与柔性立管(Flexible Riser)相比较,SCR可以承受更为恶劣的环境荷载作用,适用于多种海况,尤其在高温高压环境下,SCR凭借其诸多优点,逐渐成为了深水油气能源开发中的首选立管形式。

图1 SCR结构示意图
考虑海底接触的SCR由流线段和悬垂段2段组成,如图1所示,其中:触地点是SCR流线段与悬垂段的连接点;流线段与海床接触,在结构和外界环境载荷的共同作用下,与海床反复相互作用;悬垂段悬浮在海水中,主要受海流和波浪等环境载荷的作用。
国内外已有相关学者对钢悬链式立管的静力学特性进行了研究。FOYT等[1]指出转塔式系泊浮式生产储油卸油装置的垂向运动幅度较大,导致立管产生较大的运动响应。为提高钢悬链式立管的强度等性能,使用不同质量分布方案,即沿钢悬链式立管长度方向涂上不同密度的涂层实现立管质量的优化分布。HEJAZI等[2]考虑钢悬链式立管与海底土壤的接触特性,提出等效线性土壤刚度理念。KIM等[3]通过试验研究钢悬链式立管-土壤相互作用的机制。李艳等[4]首先对钢悬链式立管进行分类,其次阐述在设计钢悬链式立管时的主要影响因素以及设计步骤,最后分析钢悬链式立管的静态受力和动态受力,并给出钢悬链式立管的运动方程。刘贤雷[5]利用ANSYS有限元软件对模型求解得出:在静力学分析下,致使立管破坏的主要原因不是材料强度,而是累积的疲劳损伤。李传凯[6]用ANSYS有限元分析软件建立模型时,假定PIPE 59的cable单元不具有抗弯刚度也不能承受弯曲力,同时认为立管材料是均匀和各向同性的,没有考虑材料的非线性影响,认为立管在变形和运动中始终保持线弹性特点。
目前,从国内外研究现状看,诸多关于SCR的静力学研究都没有考虑到立管与海床的相互作用,若考虑SCR流线段,SCR整个结构的位移响应以及等效应力的变化情况对设计参数的敏感度,SCR强度是否满足要求都是需要研究的问题。因此,本文采用考虑管土分离的线性截断模型为研究对象,为简化p-y曲线,在立管顶端施加一固定的水平位移模拟上端浮体的水平漂移,并开展立管外径、立管壁厚、管内流体介质以及海流流速的变化对考虑海底接触的SCR位移响应和等效应力的影响。
1 设计理论及模型设计
1.1立管强度校核理论
在对考虑海底接触的钢悬链式立管进行静力学分析之后,可得到沿立管管身等效应力的大小,利用该等效应力对立管进行组合应力[7-8]校核。立管上任意一点处不同方向应力为
式中:σr为径向应力;σh为环向应力;σa轴向应力;Do为外径;Di为内径;t为壁厚;I为立管惯性矩;Po为沿立管上任一点的外压;Pi为内压;T为真实的管壁力;M为弯矩;A为立管截面积。
von Mises应力理论校核为
式中:σv为von Mises应力;σs为材料的最小屈服强度;n为安全系数,由设计工况和设计要求决定(n>1),本文中n取1.5。
1.2管土相互作用理论
本文考虑SCR与海床土体的接触特性,使用等效弹簧模拟海床土体,并用线性截断模型描述p-y曲线。立管-弹簧接触模型如图2所示。线性截断模型如图3所示。

图2 立管-弹簧接触模型

图3 等效弹簧的p-y曲线
图3中Pmax为土体极限承载力,计算公式[9]为
式中:cu为海床土体未排水抗剪强度,cu随土体埋深的增大而非线性增大;NPmax为承载力系数NP的最大值;承载力系数NP与海床沟槽宽度w、管道入土深度h以及管道外径Do有关,当w:Do=1时,NP可表示为h的函数,即
式中:a,b与h/Do的值以及管道外壁粗糙度有关a,b的取值见表1。
根据文献[9]中的经验公式,NPmax的计算公式为
管壁粗糙时:
管壁光滑时:
图3中Pt表示最大土体吸力,引入无量纲参数fsuc表征Pt(弹簧受拉)与Pmax(弹簧受压)之间的关系[10],即
单位管道长度下的弹簧刚度为
式中:Λ是与Do有关的常数。
本文选取极限承载力Pmax=5.8 kN,吸力系数fsuc=0.2,弹簧刚度K=2 500 kN/m/m作为简化p-y曲线的计算参数。基于立管-弹簧接触模型和线性截断p-y曲线模型,在ANSYS中建立SCR有限元模型,并对其进行静力分析,得到考虑海底接触的SCR的位移响应以及等效应力。
1.3立管结构参数
本文考虑钢悬链式立管与海底土壤的接触特性,SCR上端与SPAR平台相连接,下端与井口相连;钢悬链式立管总长1 865 m;假设立管所受海流的流速均匀分布;风载荷和浪载荷作用于SPAR平台,SPAR平台又作用于立管,对立管的影响为致使立管的悬挂点水平漂移10 m。SCR模型的具体参数见表2。

表2 SCR模型参数
2 分析与讨论
本文进行9种工况计算,分别讨论立管外径、立管壁厚、管内流体介质以及海流流速变化对SCR位移响应以及等效应力的影响,并进行强度校核。
2.1立管外径的影响
本部分讨论了立管外径变化对SCR位移响应以及等效应力的影响。此时,立管外径分别取0.355 6 m,0.455 6 m和0.555 6 m,立管壁厚为0.017 5 m,内部流体为油,海流为0.5 m/s的均匀流。
图4为在不同立管外径下SCR矢量位移云图,图中的x/L(无量纲长度,假设初始位置在立管与海底井口的连接处)表示最大位移量位置。由图4可知:随着立管外径的增加,SCR最大位移量及其发生的位置几乎保持不变,发生最大位移的位置靠近悬挂点。
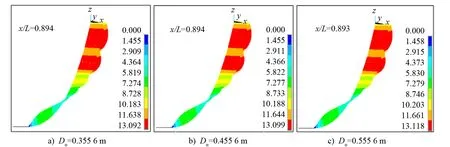
图4 不同外径对应的立管矢量位移云图

图5 不同外径对应的立管应力图
图5为在不同立管外径下SCR等效应力随立管管身的变化曲线,可以看出:随着立管外径的增加,SCR的流线段所受等效应力仅小幅度增加,悬垂段所受等效应力整体呈下降趋势;触地点处的等效应力发生了剧烈变化,从触地点到悬挂点,SCR所受等效应力呈振荡波形,峰值整体呈上升趋势,波峰之间的间距逐渐增大。SCR的最大等效应力σmax为274 MPa <σs/n),发生在Do=0.355 6 m,x/L=0.797处,符合强度设计标准。
2.2立管壁厚的影响
讨论立管壁厚变化对SCR位移响应以及等效应力的影响。此时,立管壁厚分别取0.017 5 m,0.022 5 m和0.027 5 m,立管外径为0.355 6 m,内部流体为油,海流流速为0.5 m/s的均匀流。
图6为在不同立管壁厚下SCR矢量位移云图,可以看出:随着立管壁厚的增加,SCR最大位移量小幅度减小,发生最大位移的位置靠近悬挂点。

图6 不同壁厚对应的立管矢量位移云图

图7 不同壁厚对应的立管应力图
图7为在不同立管壁厚下SCR等效应力随立管管身的变化曲线,可以看出:随着立管壁厚的增加,SCR的流线段所受等效应力小幅度减小,悬垂段所受等效应力几乎保持不变;触地点处的等效应力发生了剧烈变化,从触地点到悬挂点,SCR所受等效应力呈振荡波形,峰值整体呈上升趋势,波峰之间的间距逐渐增大。SCR的最大等效应力σmax为293 MPa <σs/n,发生在t=0.027 5 m,x/L=0.797处,符合强度设计标准。
2.3立管内部流体介质的影响
讨论立管内部流体介质的变化对SCR位移响应以及等效应力的影响。此时,内部流体介质分别为空气、油和海水,立管外径为0.355 6 m,立管壁厚为0.017 5 m,海流流速为0.5 m/s的均匀流。
图8为在不同内部流体介质下SCR矢量位移云图,可以看出:随着内部流体介质密度的增加,SCR最大位移量逐步减小,发生最大位移的位置有向悬挂点方向移动的趋势。
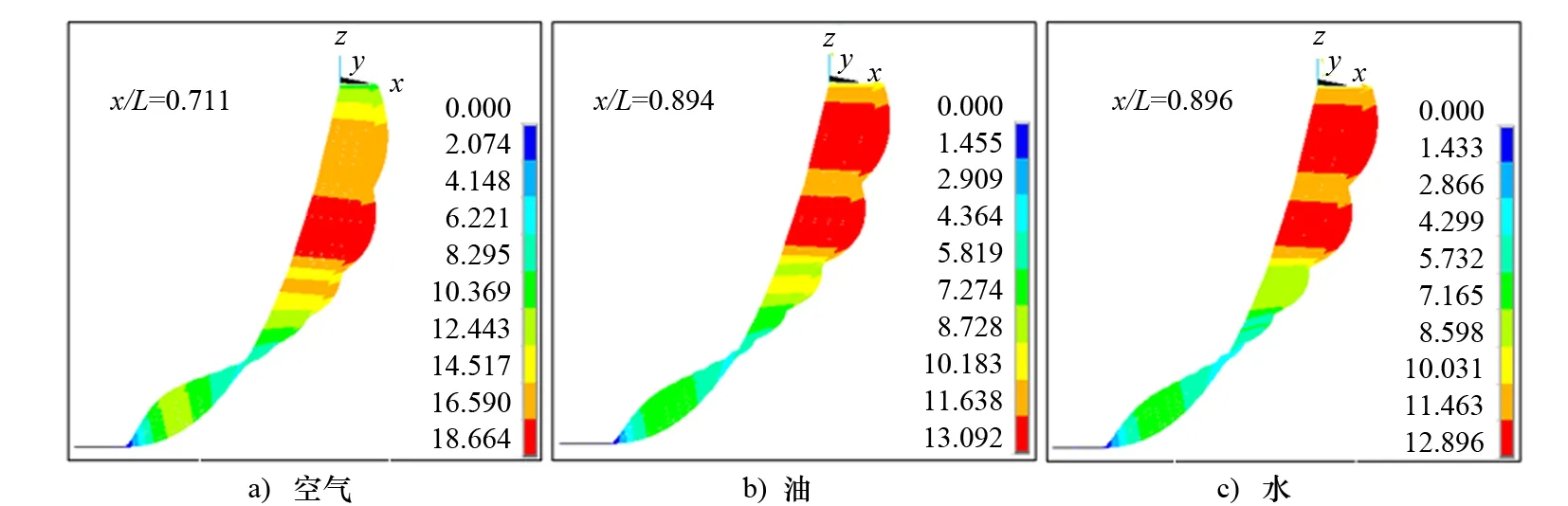
图8 不同流体对应的立管矢量位移云图

图9 不同流体对应的立管应力图
图9为在不同内部流体介质下SCR等效应力随立管管身的变化曲线,可以看出:随着内部流体介质密度的增加,SCR所受等效应力整体呈上升趋势;触地点处的等效应力发生了剧烈变化,从触地点到悬挂点,SCR所受等效应力呈振荡波形,峰值整体呈上升趋势,波峰之间的间距逐渐增大。SCR的最大等效应力σmax为283 MPa <σs/n,发生在内部流体介质为水,x/L=0.797处,符合强度设计标准。
2.4海流流速的影响
讨论海流流速的变化对SCR位移响应以及等效应力的影响。此时,海流为均匀流,流速分别取0.5 m/s,1.0 m/s和1.5 m/s,立管外径为0.355 6 m,立管壁厚为0.017 5 m,内部流体为油。
图10为在不同海流流速下SCR矢量位移云图,可以看出:随着海流流速增大,SCR最大位移量逐步增大,发生最大位移的位置逐渐向触地点方向移动。

图10 不同流速对应的立管矢量位移云图
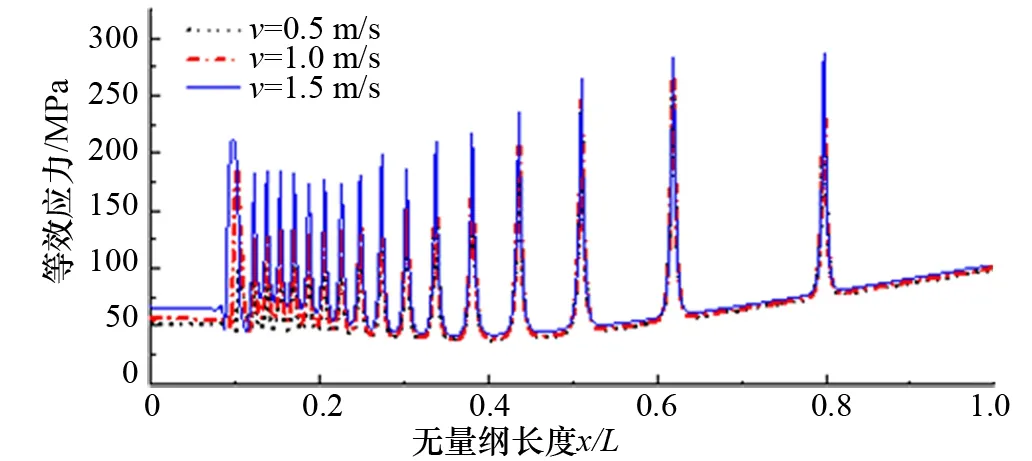
图 11 不同流速对应的立管应力图
图11为在不同海流流速下SCR等效应力随立管管身的变化曲线,可以看出:随着海流流速增大,SCR所受等效应力整体呈上升趋势;触地点处的等效应力发生了剧烈变化,从触地点到悬挂点,SCR所受等效应力呈振荡波形,峰值整体呈上升趋势,波峰之间的间距逐渐增大。SCR的最大等效应力σmax为287 MPa <σs/n,发生在v=1.5 m/s,x/L=0.797处,符合强度设计标准。
3 总 结
本文考虑钢悬链式立管流线段与海底土壤的接触特性,使用等效弹簧来模拟海床土体,利用ANSYS有限元软件,对其整体进行静力分析,研究立管外径、立管壁厚、立管内部流体介质以及海流流速对考虑海底接触的钢悬链式立管位移响应以及等效应力的影响,得出以下结论:
(1) 随着外径的增大,立管最大位移响应几乎保持不变,发生最大位移的位置靠近悬挂点;随着壁厚或内部流体密度的增大,最大位移响应呈下降趋势,发生最大位移的位置靠近悬挂点;随着海流流速的增大最大位移响应呈上升趋势,发生最大位移的位置逐渐向触地点方向移动。
(2) 随着外径的增大,流线段等效应力随着坐标位置的增加仅小幅度增加,悬垂段等效应力随着坐标位置的增加整体呈下降趋势;随着壁厚的增大,流线段等效应力随着坐标位置的增加小幅度减小,悬垂段等效应力随着坐标位置的增加几乎保持不变;随着内部流体密度和海流流速的增加,立管等效应力随着坐标位置的增加整体呈上升趋势。
(3) 悬垂段等效应力呈现振荡变化特性,且峰值之间的间距随着坐标位置的增加逐渐变大。
[ 1 ] FOYT E, GRIFFIN C, CAMPBELL M, et al. Weight Optimized SCR-Enabling Technology for Turret Moored FPSO Developments [C]// Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering, 2007.
[ 2 ] HEJAZI R, KIMIAEI M. Equivalent Linear Soil Stiffness in Fatigue Design of Steel Catenary Risers [J]. Ocean Engineering, 2016, 111: 493-507.
[ 3 ] KIM W J, NEWLIN J A, HAWS J H. Experimental and Analytical Investigation of Soil/SCR Interaction Under VIV [C]//Proceedings of the International Offshore and Polar Engineering Conference, California, USA, 2006.
[ 4 ] 李艳,李欣,罗勇,等.深水钢悬链线立管(SCR)的设计与研究进展[J]. 中国海洋平台,2013,28(02):7-13.
[ 5 ] 刘贤雷. 钢悬链线立管静力及涡激疲劳损伤研究[D]. 天津:天津大学,2010.
[ 6 ] 李传凯.钢悬链线立管静力及波激疲劳分析[D]. 大连:大连理工大学,2008.
[ 7 ] 于洪旭, 杨琥, 冯现洪. 钢悬链式深水立管壁厚选择研究[C]//第十七届中国科协年会, 2015.
[ 8 ] 王凤莲, 李秀锋. 深水钢悬链式立管 (SCR) 强度分析方法研究[J]. 科技经济导刊, 2016(08): 1-2.
[ 9 ] AUBENY C P, BISCONTIN G, ZHANG J. Seafloor Interaction with Steel Catenary Risers[D]. Texas:Texas A&M University, 2006.
[10] 杜金新. 海洋立管-海床土体接触作用数值分析[J]. 工程地质计算机应用, 2008 (04): 6-11.
StaticBehaviorofSteelCatenaryRiserConsideringSeabedContact
CHEN Xiang, WANG Xiaomei, GAO Yun, CHANG Bei, CHENG Junlin
(State Key Laboratory of Oil and Gas Reservoir Geology and Exploration, Southwest Petroleum University, Chengdu 610500, Sichuan, China)
Based on the structural characteristics of the Steel Catenary Riser(SCR) considering seabed contact, a linear truncation model considering pipe-soil separation are used to describe p-y curves. The displacement response and equivalent stress of the riser are analyzed by changing the riser diameter, the riser wall thickness, the pipe fluid medium and the current velocity. The horizontal displacement at the top of the riser is used to simulate the horizontal drift of the upper body. The results indicate that the vertical displacement response is a downward trend with the increase of wall thickness and internal fluid density,and with the increase of current velocity, the vertical displacement response is a rising trend. The influence of the outside diameter on the displacement response of the riser tube is not significant. The equivalent stress has changed dramatically on touch down point. From touch down point to hang off point, equivalent stress of riser is the oscillation waveform peak and the peak value is a upward trend, and the distance between wave crests increases gradually. It is concluded that the displacement response of the riser is mainly affected by the wall thickness of the riser, the internal fluid density, and the current flow velocity. The equivalent stress of the riser is mainly affected by the internal fluid density and the current flow velocity.
Steel Catenary Riser(SCR); seabed contact; displacement response; equivalent stress
O357
A
2017-02-17
国家自然科学基金资助项目 (51609206, 51522902, 51379033) ;国家留学基金资助项目(201608515007)
陈 祥(1978-),男,本科
1001-4500(2017)05-0082-07

