有限水深海流感应电磁场数值模拟❋
朱心宇, 李予国,2❋❋
(1.中国海洋大学海洋地球科学学院,山东 青岛 266100;2.青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237)
海水是良导体,处于不停地运动之中。根据法拉第定律和安培定律,运动的海水因切割地磁场而产生感应电流,从而产生感应电磁场。人们在研究海流感应电磁场时,通常只考虑地磁场垂直分量的作用。在两极及其附近区域,磁力线与地表近乎垂直,只考虑地磁场垂直分量的作用是合适的。在低纬度地区,地磁场水平分量会对海流感应电磁场产生一定的影响。因而研究地磁场三分量作用下的海流感应电磁场很有意义。在计算海流感应电磁场时,通常假定海水的电导率是均匀不变的,而实际上海水电导率随海水温度和盐度的变化而变化,故而研究变化的海水电导率产生的海流感应电磁场很有必要。
海流感应电磁场的研究始于20世纪50年代,Longuet-Higgins等分析了表面波和稳定海流引起的电场及电流[1]。Sanford计算了带地形的一维大尺度低频海流感应磁场[2]。Chave用格林函数法计算海水运动感应电磁场,分析了表面重力波和开尔文波感应电磁场的特征[3]。Larsen等推导了海流中任意两点间电势差表达式,分析了大尺度海流感应电场的分布[4]。陈标等计算了地磁场垂直分量作用下宽海流产生的感应磁场,研究表明当海流宽度较大时,海流感应磁场不应被忽略[5]。林春生等根据电磁感应原理分别讨论了地磁场水平分量和垂直分量作用下的海流感应电场[6]。李洪平结合世界地磁场模型WMM2005,计算了地磁场垂直分量作用下海流产生的感应磁场[7]。张自力模拟了地磁场垂直分量作用下海流感应电磁场[8]。Bhatt采用格林函数法计算了地磁场垂直分量作用下一维和二维匀速海水运动感应电磁场[9]。
本文利用麦克斯韦方程推导出地磁场三分量作用下一维海流感应磁场表达式,构建了海流-地电模型,模拟地磁场三分量作用下的海流感应电磁场,分析了地磁场水平分量对海流感应电磁场的影响,并分析了不同海流速度以及变化的海水电导率产生的海流感应电磁场特征。
1 方法原理
1.1 海水运动感应电磁场控制方程
在忽略位移电流的情况下,海水运动产生的感应电磁场满足如下麦克斯韦方程:
▽×H=σE+σμ[v×(F+H)],
(1)
(2)
式中:F为地磁场;H为感应磁场;v为海水运动速度;σ为介质电导率;μ=4π×10-7Vs/Am,为真空磁导率。由于海水运动产生的磁场|H|远小于地磁场|F|,故可用F代替式(1)中的F+H。
假设海水运动速度v是谐变的(e-iωt),ω=2π/T为角频率,T为海水运动周期,则方程(1)和(2)式可写成:
▽×H=σ[E+μ(v×F)],
(3)
▽×E=iωμH。
(4)
由式(3)和式(4),可以得到海水运动感应磁场所满足的偏微分方程:
▽2H-k2H=-μσ▽×(v×F)。
(5)
式中:k2=-iωμσ,(Re(k)>0),k称为波数。
1.2 海流感应电磁场表达式
考虑如图1所示的海流-地电模型,它由海流、海水和海底基岩构成。建立直角坐标系(x,y,z),坐标原点位于海流顶界面中心,z轴正向垂直向下。假设海流宽度为b,海流底界面深度为h1,海水深度为h2,海流、海水和海底基岩的电导率分别为σ1、σ2和σ3。

图1 海流-地电模型Fig.1 Ocean current model
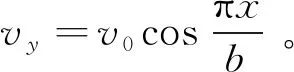
满足的亥姆霍兹方程:
(6)
采用分离变量法求解方程(6),可得到磁场水平分量Hy的表达式:
(7)
式中
(8)
结合(3)式,可得到电场分量Ex的表达式。
方程(7)中的A和B为待求系数。为了得到A和B,必需利用如下边界条件:(1)在水平分界面上,海流感应电场和磁场的切向分量连续;(2)在空气-海水界面上,电流密度的垂直分量为零;(3)在海底下半空间中,当z→∞时,感应磁场衰减至零。
2 海流感应电磁场
假定图1所示模型中,海水深度为3 100 m,海流厚度为500 m,海流宽度为10 km,海流速度v0为0.1 m/s,运动周期为10 s。海流、海水和海底基岩的电导率分别为3.3、3.3和1.0 S/m。
利用上一节所述计算方法及公式,计算北极附近某点(90°00′00″N,110°00′00″E)的海流感应电磁场。基于国际地磁场模型WMM2015,计算得到该点地磁场水平分量为-543.2 nT,垂直分量为56 718.4 nT。利用本文方法可以得到该点地磁场三分量作用下的海流感应电磁场振幅随深度变化曲线,如图2所示。

((a)电场Ex Electric fields; (b)磁场By Magnetic field.)
为了验证前述方法和程序的正确性,图2中也绘出了地磁场垂直分量作用下的海流感应电磁场曲线[10]。图中红色曲线为地磁场垂直分量作用下的海流感应电场和感应磁场振幅随深度变化曲线,蓝色曲线为地磁场三分量作用下的海流感应电场和感应磁场振幅随深度变化曲线。由图2可知:
(1)当纬度为90°N时,地磁场垂直分量作用下的海流感应电磁场曲线与地磁场三分量作用下的海流感应电磁场曲线重合。
(2)电场水平分量Ex在海表面处有最大值2.964 5 μV/m,但随着深度的增加而减小,在海底界面处达到最小值0.129 0 μV/m;磁场水平分量By在海表面处取最小值0.011 nT,且随着深度的增加而增大;在海流底界面处达到最大值5.736 1 nT,然后By开始减小。
假定计算点的经纬度为(20°00′00″N,110°00′00″E)。利用国际地磁场模型WMM2015计算得知,该点地磁场值水平分量为27 489.6 nT,垂直分量为28 335.5 nT。图3绘出地磁场三分量作用下海流感应电磁场振幅随深度变化曲线。为了比较起见,图3中也绘出了地磁场垂直分量作用下的海流感应电磁场曲线。由图3可知,两种情形下感应电磁场随深度变化曲线的形态类似,但幅值相差较大。地磁场三分量作用下的海流感应电场和磁场的最大值分别为2.271 5 μV/m和4.405 5 nT,但地磁场垂直分量作用下的海流感应电场和磁场的最大值分别1.488 7 μV/m和2.880 1 nT,电场和磁场最大值降低了大约35%。可见,研究低纬度地区海流感应电磁场时,地磁场水平分量的影响不应被忽略。
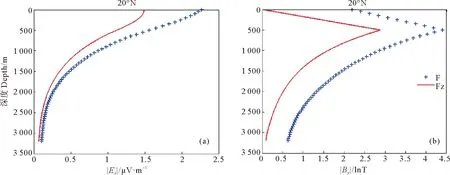
((a)电场Ex Electric fields;(b)磁场By Magnetic field.)图3 低纬度测点地磁场三分量作用下的海流感应电磁场与地磁场垂直分量作用下的海流感应电磁场对比Fig.3EM fields induced by ocean current with considering three components of the Earth’s magnetic fieldin low latitudes, compared to those obtained with only considering vertical component
地磁场水平分量随纬度增大而逐渐减小,其对海流感应电磁场的影响也随之减少。沿110°E经度线,从赤道到北极,纬度每增加10°选取一个计算点,分别计算每个点处地磁场垂直分量作用下和地磁场三分量作用下的海流感应电磁场。首先利用国际地磁场模型WMM2015计算得到各观测点的地磁场值,然后分别计算地磁场三分量和地磁场垂直分量作用下各个深度处的海流感应磁场,选取各观测点两种情形下感应磁场最大值,并计算其相对差。图4为沿经度线上地磁场三分量和地磁场垂直分量作用下的海流感应磁场最大值相对差与地磁场三分量作用下海流感应电磁场最大值之比。
由图4可知,在赤道处,地磁场水平分量对海流感应磁场的影响很大。随着纬度的增加,地磁场水平分量对海流感应磁场的影响逐渐减小。当纬度增大到80°N(或80°S)时,地磁场水平分量对海流感应磁场的影响降到1.4%。可见,在80°N~90°N(或80°S~90°S)区域内,地磁场水平分量对海流感应磁场影响可以忽略,模拟海流感应电磁场时可以只考虑地磁场垂直分量。而在0°N~80°N(或0°S~80°S)区域内,地磁场水平分量对海流感应电磁场的影响较大,模拟海流感应电磁场时应将地磁场水平分量的影响考虑在内。
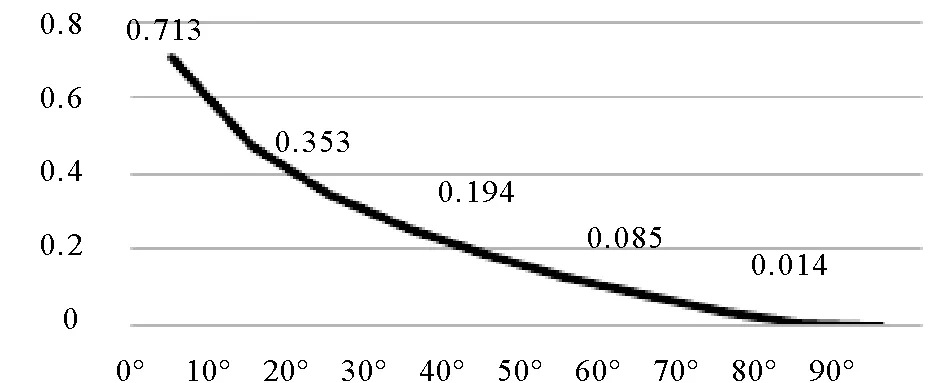
图4 地磁场水平分量对海流感应磁场的影响Fig.4 Impact of the horizontal component of the Earth’s magnetic field on the induced field
3 海流感应电磁场模拟及特征分析
3.1 海流速度对海流感应电磁场的影响
海流感应电磁场的幅值主要取决于海流速度及海流厚度[8]。下面,我们讨论海流速度对海流感应电磁场的影响。
图5绘出三个不同海流速度(v0=1、0.75、0.5 m/s)情形下海流感应电磁场随深度变化曲线。由图5可知:
(1)海流感应电场强度与海流速度正相关。海流速度越大,感应电场值越大,衰减的也越快。海流速度为1、0.75和0.5 m/s时,相应的感应电场最大值分别为22.715 4,17.036 6和11.357 7 μV/m,即海流速度每增大0.25 m/s,感应电场最大值增大约 5.68 μV/m。
(2)海流感应磁场强度亦与海流速度正相关。海流速度越大,其产生的感应磁场越大。在海流层内,海流速度越大,感应磁场增长越快。在海流底界面处,感应磁场达到极大值。海流速度为1、0.75和0.5 m/s时,相应的感应磁场最大值分别为44.054 9 ,33.041 2,22.027 5 nT,即海流速度每增大0.25 m/s,感应磁场最大值增大约11.013 7 nT。可见海流速度对其感应磁场具有明显的影响。

((a)电场Ex Electric fields;(b)磁场By Magnetic field.)
3.2 变化的海水电导率对海流感应电磁场的影响
在模拟海流感应电磁场时,通常假设海水的电导率是均匀不变的,而实际上海水的电导率与海水的盐度、温度等因素有关。随着深度的增加,海水的盐度和温度降低,海水电导率也随之减小。
考虑如图6所示海流-地电模型。假设海水深度为400 m, 海流厚度为300 m,海流速度为0.1 m/s。假设海流层可以分为三层:0~100 m,电导率为σ1=5.0 S/m;100~200 m,电导率为σ2=4.2 S/m;200~300 m,电导率为σ3=3.3 S/m。300~400 m为海水层,海水的电导率为σ4=3.3 S/m。海底基岩电导率为σ5=1.0 S/m。
图7绘出图6所示海流-地电模型的海流感应电场和感应磁场随深度变化曲线。图中绿色曲线为变化的海水电导率情况下海流感应电磁场振幅随深度变化曲线。为了比较起见,图7中也绘出了海流层电导率均匀不变时,海流感应电场和磁场随深度变化曲线,图中蓝色、红色和青色曲线表示海流层电导率分别为5.0,4.2和3.3 S/m时的计算结果。由图7可知:
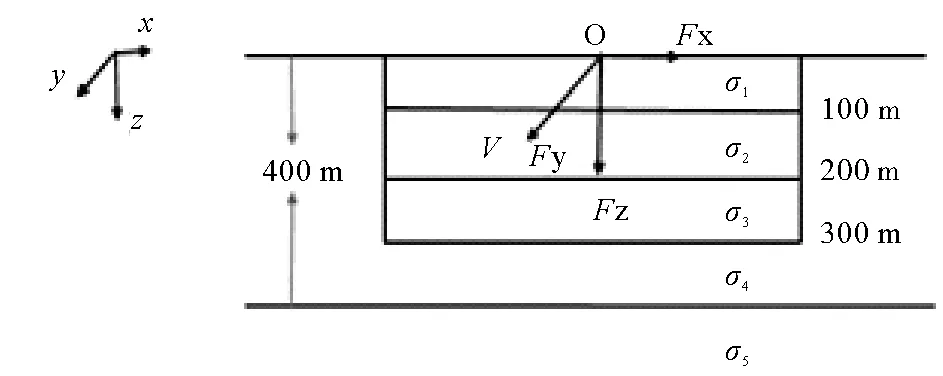
图6 海水电导率分层变化的海流-地电模型 Fig.6 Ocean current model with variable seawater conductivity
(1)当海流层电导率均匀不变时,海流感应电场与海流电导率正相关。海流电导率越大,电场振幅越大。电导率增大约1 S/m,感应电场振幅最大值增大约0.005 μV/m。当海流层电导率分层变化时,感应电场振幅最大值增大约0.05 μV/m,可见变化的海水电导率对海流感应电场值具有较明显的影响。

((a)电场Ex Electric fields;(b)磁场By Magnetic field)
(2)在海表面处,不同海水电导率情况下海流感应磁场By幅值相近,约为 2.2 nT。随着深度的增加,By快速增大,在海流底界面处,感应磁场达到极大值。在海流层内,海流电导率越大,感应磁场增长越快,同一深度的感应磁场越大。海流电导率每增大1 S/m,感应磁场最大值增大约0.2 nT,即感应磁场振幅值增大约5%。可见海流电导率对其感应磁场具有明显的影响。当海流层电导率分层变化时, 感应磁场非线性增长,且增长速率与海流电导率有关。
4 结语
本文推导了地磁场三分量作用下的一维海流感应磁场表达式,建立海流-地电模型,模拟和分析了地磁场水平分量对海流感应电磁场的影响。算例表明,地磁场水平分量对海流感应电磁场的影响随着纬度的降低而增大,在模拟较低纬度处海流感应电磁场时,应将地磁场水平分量的影响考虑在内。海流速度与海流感应电磁场正相关,海流速度越大,其感应电磁场越大,且衰减越快。变化的海水电导率对海流感应电场具有较明显的影响。

