利用Elman神经网络预测三元水盐体系相平衡溶解度❋
孟宪泽, 付云朋, 袁俊生, 李 斌
(1.中国海洋大学 海洋化学理论与工程技术教育部重点实验室,山东 青岛 266100; 2.中国海洋大学 化学化工学院,山东 青岛 266100; 3.河北工业大学 化工学院,天津 300130; 4.泉州师范学院 化工与材料学院,福建 泉州 362000)
水盐体系相平衡的实验与理论研究有助于指导盐化工、煤化工、精细化工等行业的高盐卤水资源化利用工艺的形成与优化[1-3]。数十年来,研究者通过繁琐的实验方法获得了大量的相平衡数据。随着Debye-Hückel理论的提出[4],通过热力学理论估算水盐体系的固-液相平衡溶解度开始进入人们的视野。半经验半理论的Pitzer模型建立了渗透系数、活度系数和溶液超额Gibbs自由能之间的关系[5]。改进的Pitzer模型,如HMW模型、PSC模型等,将热力学模型的适用范围拓展到了混合电解质溶液体系,至今被广泛采用[6-8]。Zhao和Song结合密度泛函理论提出了一种统计力学模型[9],成功预测了典型三元相图,并被证明是一种通用高效的预测方法。考虑到离子水化效应,基于E-UNIFAC模型的Lu-M单级水化模型通过计算溶液各组分的活度系数来得到相平衡溶解度[10]。陆小华以Lu-M模型为基础编制了电解质溶液相平衡计算软件包PHEES,Yuan以HMW模型为基础编制了简单三元体系相平衡软件CalPha,为相应三离子体系的溶解度预测提供了便利。
随着人工智能技术的发展,神经网络在预测、函数拟合、模式识别等方面的独特优势引起人们的关注[11-13]。Elman神经网络(Elman neural network, ENN)相对于经典的反向传播神经网络(back propagation neural network, BPNN)而言,引入了上下文单元(context units, CU)层,使之具有了短时记忆的特性,展现出更优的学习能力和泛化能力。Wang,Li和Akhil等基于ENN的延时特点,将其应用于锂离子电池寿命预测[14-15],X射线荧光光谱的分析[16]和室内空气质量进行评估预测[17]。以上应用均显示出ENN优异的性能与泛化能力,而其在水盐体系相平衡中的应用至今鲜有报道。
本文以溶解度数据的文献值与ENN预测值的均方误差(MSE)作为指标,考察了隐含层数,神经元数目,不同学习函数对模型训练效果的影响,获得了最优的ENN拓扑结构。通过与文献值、HMW模型计算值对比,分析了ENN在精确度和运算速度方面的优势。运用优化的ENN-(2,3)GDX模型对未发表的15.0 ℃下NaCl-KCl-H2O体系、87.5 ℃下Na2SO4-MgSO4-H2O体系、60.0 ℃下KCl-K2SO4-H2O体系和60.0 ℃下NaCl-Na2CO3-H2O体系的平衡溶解度进行了预测。
1 ENN结构概述
ENN包含输入层、隐含层和输出层(见图1)。相比于常见的BPNN,ENN在隐含层中增加了一个CU层,将前一步的输出值作为一步延时算子,返回神经元作为线性加权。CU层增强了ENN对历史信息的敏感性[18-19],提高了神经网络应对突变的能力,特别适合于包含突变点的水盐体系平衡溶解度的预测。

图1 ENN模型拓扑结构
ENN隐含层神经元传递函数fj的数学表达如式1所示:
(1)

ENN输出层神经元传递函数gj的数学表达如式2所示。输出层(O)神经元不包含隐含层神经元中的延时算子。
(2)
2 建模数据采集
本文收集了海水体系Na+, K+, Ca2+, Mg2+// Cl-, SO42-, CO32-, HCO3-, B4O72--H2O的15个三元子系统的数据[20-21]用于ENN的训练,温度范围为0.0~150.0 ℃。系统组成与数据集信息如表1所示。按照80.0%和20.0%的比例将数据点随机分配为训练集和验证集。训练集用来训练构建好的ENN模型,验证集数据与模型预测值的均方误差(MSE)作为评估模型性能的指标。

表1 数据点采集信息
3 结果与讨论
3.1 ENN建模与拓扑结构优化
以MgCl2-MgSO4-H2O体系为例,MgSO4的在溶液中的平衡浓度(CMS)受系统温度(T)与MgCl2浓度(CMC)影响。视T与CMC为输入参数,视CMS为有导师学习的输出参数,如式3所示。以CMC作为输出参数时表达式同理。
CMS=f(T,CMS)。
(3)
将数据集遵循80.0%、20.0%的比例随机分配为训练集和验证集。训练集的输入参数和输出参数一一对应,导入ENN进行训练。验证集的输入参数导入训练好的神经网络进行训练,将神经网络的预测结果与验证集的输出参数求得MSE作为指标,用以验证ENN模型性能。
影响ENN性能的因素主要包括网络结构,训练函数等。含有两层以上隐含层的深层神经网络已经被证实能够提升浅层神经网络的学习速率和收敛速率,且能够在一定程度上提升预测结果的准确性[22]。此外,选取合适的训练函数也能够优化收敛速率,避免陷于局部极小值,提升神经网络预测精度。因此,有必要将ENN隐含层神经元数量与学习函数作为变量,以探究最优神经网络拓扑结构。常见的训练函数包含L-M反向传播算法(Levenberg-Marquardt backpropagation, L-M),带动量的梯度下降的自适应学习率的反向传播算法(Gradient descent with momentum and adaptive learning rate backpropagation, GDX)和自适应学习速率的梯度下降反向传播算法(Gradient descent with adaptive learning rate backpropagation, GDA)[23]。隐含层设置为2层,每层神经元数量为2~5,训练函数分别选用LM、GDX和GDA算法分三次建模,建模因素分布如表2所示。

表2 ENN建模因素分布
图2所示为基于LM/GDX/GDA学习函数的神经网络MSE热力图,横坐标对应实验因素(Factors No.),纵坐标对应三元水盐子系统编号(System No.)。在预测结果精确度方面,图2(b)具有较低的MSE,说明GDX学习函数在运算精度上具有优势。图3所示为ENN-GDX的预测精度受神经网络拓扑结构变化的影响。当layer Ⅰ 取值为2时,建模因素为F-1, F-8, F-9 和 F-16,逐渐增大layer Ⅱ 神经元数量,系统MSE值呈现先下降后升高的趋势,F-8对应的2-3神经元结构MSE值为0.70×10-2,预测精确度最高。当layer取值为3时,建模因素为F-2, F-7, F-10 和 F-15,MSE值均大于1.00×10-2,说明Layer Ⅰ 为3的模型预测精度较低。当layer Ⅰ 取值为4时,建模因素为F-3, F-6, F-11 和F-14,参数F-6对应的神经网络MSE值为0.76×10-2,性能优于其他三组。当layer Ⅰ 取值为5时,建模因素为F-4, F-5, F-12 和 F-13,其中F-4和F-5的神经网络MSE值为0.86×10-2。综上所述,单纯增大隐含层的神经元数量不是提高神经网络性能的充分必要条件。最终,ENN的最优拓扑结构设定为(2,3)-GDX,即隐含层Ⅰ包含2个神经元,隐含层Ⅱ包含3个神经元,学习函数采用GDX。

图3 ENN-GDX模型子系统MSE平均值

3.2 模型性能分析
参考图2,以预测精度较低的NaCl-CaCl2-H2O (F-8,S-3)体系作为研究对象,将神经网络的预测值对比文献值和HMW模型的计算值,考察ENN-(2,3)GDX的网络性能。HMW模型中,各溶质的活度系数依照公式(4)~(7)计算得出。

(a. LM学习函数 LM training function; b. GDX学习函数 GDX training function; c. GDA学习函数 GDA training function.)图2 基于三种不同学习函数的ENN性能(MSE)分布图
(4)

(5)

(6)

(7)
式中:C/C′和A/A′分别对应阳离子和阴离子;mC和ZC表示阳离子C的摩尔数和电荷量;Ψ是三元离子相互作用参数;φφ、φ和φ′是与离子强度有关的第二维里系数。上式中未知参数由公式(8)~(13)计算。
(8)
(9)
(10)

(11)

(12)
式中:Bφ和B是与离子强度有关的第二个维里系数;B′是B对离子强度的微分。水的活度系数由公式(13)得出。
lnαw=-φ∑(mi/55.51)。
(13)
图4所示为25.0 ℃下NaCl-CaCl2-H2O体系平衡溶解度的模型计算值与文献值[21]。ENN-(2,3)GDX模型的预测值取5次计算的平均(见表3)。CaCl2wt.%预测值相对文献值的相对误差为2.60%,NaCl wt.%为2.40%。红色误差棒为运用ENN-(2,3)GDX模型,在确定的NaCl浓度下预测的CaCl2浓度,蓝色误差棒为在确定的CaCl2浓度下与之平衡的NaCl浓度。橙色虚线表示运用HMW模型计算所得液相线。ENN-(2,3)GDX模型的预测值更接近于文献值,预测误差小于HMW模型。对于HMW模型而言,若离子相互作用参数与电解质的Pitzer参数是已知的,则可以通过编程实现快速运算,否则仍需要通过繁琐实验方法求得该温度下的物理参数,然后再进行液相线的测算。而对于ENN模型,不存在物理参数的求解过程,因此在运算速度上具有优势。

表3 ENN-(2,3)GDX模型5次预测结果

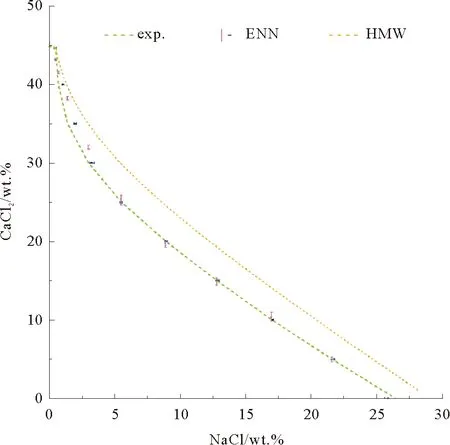
图4 25.0 ℃下NaCl-CaCl2-H2O体系液相线的文献值和ENN-(2,3)GDX模型、HMW模型预测值
3.3 液相线预测
本文运用ENN-(2,3)GDX模型,对未知温度体系的液相线进行预测。参考图2中不同系统的MSE分布图研究对象选择为预测误差偏高的四组系统:S-1、S-8、S-9和S-14。对应体系的预测温度分别为15.0、87.5、60.0和60.0 ℃,预测结果取5次运算的平均值。预测结果如图5和支撑文件表S1~S4所示。由图5可知,在S-8,S-14体系中的液相线对应多种复杂的平衡固相,虽然ENN-(2,3)GDX模型的个别预测值的相对偏差较大,但共饱点的预测结果稳定,预测液相线也能够较好地符合随温度的变化趋势。可以认为ENN-(2,3)GDX模型是一种有效的预测三元水盐体系相平衡溶解度的神经网络模型。

(ENN, Elman网络预测值; exp., 实验值 ENN, predicted value by Elman neural network; exp. experimental value.)图5 S-1、S-8、S-9和S-14系统的预测液相线
4 结语
运用Elman神经网络建立了预测三元水盐体系相平衡溶解度的ENN-(2,3)GDX模型。通过对比文献中25.0 ℃下NaCl-CaCl2-H2O体系的预测液相线可知,ENN-(2,3)GDX模型在运算精度和速度方面均优于传统的HMW热力学模型。对未发表的简单和复杂三元体系:NaCl-KCl-H2O体系(15.0 ℃)、Na2SO4-MgSO4-H2O体系(87.5 ℃)、KCl-K2SO4-H2O体系(60.0 ℃)和NaCl-Na2CO3-H2O体系(60.0 ℃)的平衡溶解度进行了预测,结果显示,神将网络模型预测得到的液相线能够较好地符合温度变化趋势,共饱点预测值稳定,体现出ENN-(2,3)GDX模型在预测三元水盐体系溶解度上的优异性能。

