基于复相关相位斜率的海面弱小目标检测方法❋

程孝龙， 姬光荣

(中国海洋大学信息科学与工程学院，山东 青岛 266100)

海杂波背景下的海面弱小目标通常具有较小的雷达回波强度和较低的多普勒速度，很容易被淹没在海杂波信号中，可探测性较低，是目前涉海雷达面临的一个难题。尤其是对于高分辨率雷达而言，由于“海尖峰”现象[1-2]的存在，使得海面弱小目标的可探测性进一步降低。

传统恒虚警检测[3-5]和分型特征[6-7]检测等目标检测方法主要是基于雷达信号的幅度特征，海杂波幅度统计特征研究经历时间最长也最为成熟，但是基于幅度特征的目标检测方法性能一直没有新的突破，也渐渐无法满足现代军事发展的需求，这就要求我们从新的领域或者新的角度进行海杂波背景下的目标检测方法研究。

从雷达信号处理角度来看，改善海杂波背景下目标检测方法主要有两种途径：一种途径是在理论上获得突破性进展，彻底颠覆现有目标检测方法体系；另一种途径是引入新的特征，从完全不同的角度或维度进行目标检测方法研究。前一种途径是研究人员孜孜以求的长期目标，不管面临的困难有多么巨大，人类都需要进行积极地努力争取突破。而后一种是短期内比较可行的途径，尝试用新的特征进行目标检测方法研究，

打破现有理论成果的束缚，有很大的几率可以提升目标检测方法效率。

在现有目标检测方法研究[8-11]中，虽然雷达信号的自相关特性是一种非常重要的统计特征，但是只被作为一种参考量而已，研究人员关心的只是雷达信号的去相关时间或去相关距离，导致现有海杂波自相关特性研究都是在实数领域进行的，即便是面对复数形式的雷达信号，也都将信号取模后再进行相关系数计算，或者将复数信号进行相关系数计算后再取模，这就意味着人们“故意”丢失了自相关系数的相位信息。

在信号处理领域中，相位信息在有着举足轻重的作用，因为实信号只能存在于平面中，而包含相位信息的复信号则是在立体空间中进行传播的，相当于扩展了信号的维度，这就带来了新的研究方向，因此我们可以推断雷达信号自相关系数的相位信息在目标检测领域将有着非常巨大的潜力。

本文将从海杂波复数域下的时间自相关特性(以下称复相关)研究入手，分析复相关系数的统计特性，尤其是复相关系数相位信息的统计特性。然后对比目标单元与杂波单元复相关相位分布的差异性，并利用这种差异性进行目标检测方法研究。

1 海杂波复相关统计特性

对于复数形式的海杂波时间序列，其归一化的自相关系数计算公式可表示为

(1)

式中：z(k)为零均值化处理后的海杂波时间序列;N为序列长度;τ为时间延迟。

以1993年IPIX雷达实验320#海杂波数据为例，该组数据具有14个距离门，脉冲重复频率为1 000 Hz，包含131 072个脉冲，记录时长大约131 s。

首先提取其中一个纯杂波距离单元数据z(k)，并将其包含的131 072个脉冲进行分组，每组含有256个脉冲序列，构成512组时间子序列zi(k)，并对每一组时间子序列zi(k)按照公式(1)进行复相关计算，获得复相关系数Ri(τ)。复相关系数Ri(τ)包含幅值和相位信息，因此可以通过极坐标进行展示，如图1所示。

图1 海杂波复相关系数

图1中浅色曲线簇为同一距离门内512组时间子序列zi(k)的复相关系数分布曲线图，深色曲线为其中某一组时间子序列的复相关系数分布曲线。

从图1可以发现：

(1)海杂波复相关系数Ri(τ)在极坐标中呈螺旋状分布，并且都是以(1.0，0)为起点，无限逼近极坐标中心点(0.0，0)；

(2)同一距离门内各时间子序列，其复相关系数的旋转方向是一致的，并且复相关系数的分布比较集中。

进一步提取复相关系数Ri(τ)的相位信息pi(τ)，并对其解缠绕处理，如图2所示。

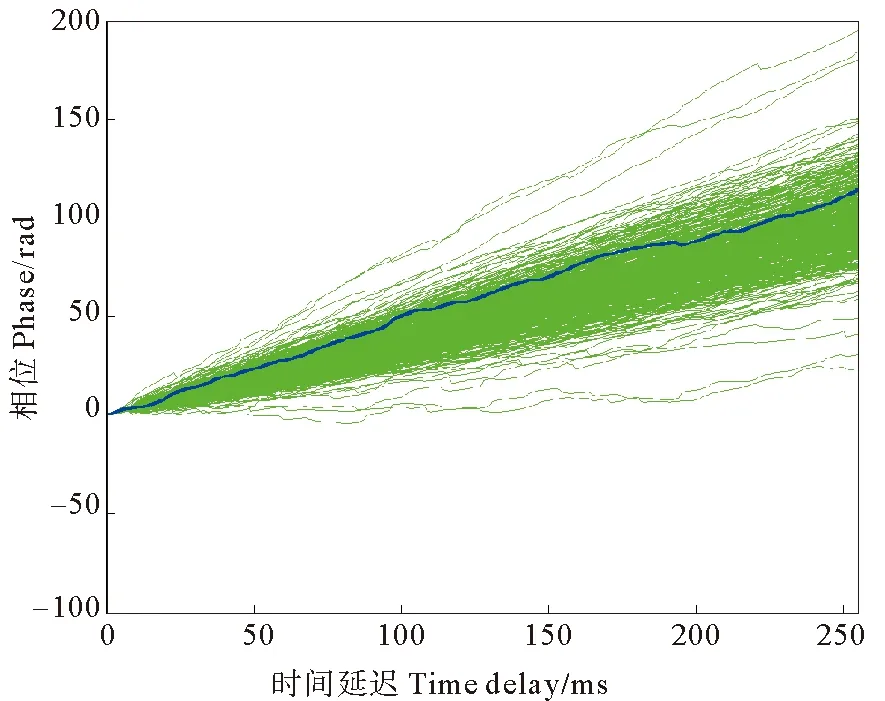
图2 复相关相位分布

图2中浅色曲线簇为同一个距离门内512组时间子序列复相关系数的相位分布，深色曲线为其中某一组时间子序列复相关系数的相位分布。从中可以发现，海杂波复相关系数的相位信息呈线性分布。

对于线性分布的信号来说，我们最感兴趣的是其随时间变化的速率，因此我们提出一个全新的统计特征——复相关相位斜率：复相关系数的相位信息pi(τ)随时间延迟τ变化的速率。

利用最小二乘法可以对复相关系数的相位信息pi(τ)进行线性拟合，然后统计同一距离单元内的512组时间子序列复相关相位斜率的分布情况。

我们将杂波距离单元与目标距离单元的复相关相位斜率的概率密度函数进行对比，结果如图3所示。

图3 复相关相位斜率概率密度函数

图3中实线为目标单元复相关相位斜率概率密度函数曲线，虚线为杂波单元复相关相位斜率概率密度函数曲线。

从图3可以看出，目标单元与杂波单元的复相关相位斜率概率密度函数基本上都符合正态分布。目标单元复相关相位斜率的概率密度函数曲线比较扁平，其在正态分布模型中的方差较大，说明相位分布比较分散；而杂波单元复相关相位斜率的概率密度函数曲线比较尖锐，其在正态分布模型中方差较小，说明相位分布比较集中。

从图3还可发现，目标单元复相关相位斜率的概率密度函数曲线与杂波单元复相关相位斜率的概率密度函数曲线均值差异非常明显，且两条曲线交集区域面积较小，很容易将目标单元与杂波单元进行区分，这表明复相关相位斜率特征可以作为一种目标识别的特征量。

假设以目标单元与杂波单元的概率密度曲线的交点位置作为目标检测的判别门限，可对比使用复相关相位斜率和功率谱密度两种不同特征的目标检测效果(见图4)。

图4 目标与杂波分布特性

图4(a)为目标单元与杂波单元功率概率密度分布曲线，图4(b)为目标单元与杂波单元复相关相位斜率概率密度函数曲线。图4中实线为目标单元概率密度函数，虚线为杂波概率密度曲线，点线代表目标检测门限。

从图4可以发现，目标单元与杂波单元功率概率密度函数曲线的重合区域面积比较大，而目标单元与杂波单元复相关相位斜率概率密度函数曲线的重合区域面积比较小。假设以目标单元与杂波单元概率密度函数曲线的交点位置作为判别门限进行目标检测，以信号功率特征进行目标检测，检测概率为60.34%，虚警概率高达16.02%；而以复相关相位斜率特征进行目标检测，检测概率高达91.60%，虚警概率仅为2.93%。

这证明了复相关相位斜率特征比功率谱特征或幅度特征更适合目标检测应用，是一种全新的有效的目标检测特征。

2 目标检测方法设计

针对复相关相位斜率特征，我们设计了如图5所示的目标检测方法。

图5 目标检测方法示意图

目标检测方法绝大多数是在某一种特征空间内进行的，特征空间的选取对检测方法效率十分重要，对于本文提出的基于复相关相位斜率特征的目标检测方法而言，获得复相关相位斜率特征矩阵十分关键。

按照图5所示的目标检测方法，需要将海杂波背景下的实测雷达数据进行特征空间转换，即从幅度特征空间转换到复相关相位斜率特征空间，特征空间转换具体过程如下：

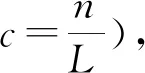
(2)对子序列矩阵G[m,c]中每一个元素都进行复相关系数计算，并提取相位信息，构建复相关相位矩阵P[m,c]，复相关相位矩阵P[m,c]中每一个元素都代表一段长度为L的相位序列。

(3)对复相关相位矩阵P[m,c]中每一个元素都进行相位线性拟合，获得各组相位信息的斜率，并构建复相关相位斜率矩阵K[m,c]。

至此，完成了海杂波数据S[m,n]从幅度特征空间到复相关相位斜率特征空间的转换，获得了复相关相位斜率特征矩阵K[m,c]。

仍以1993年IPIX雷达实验320#数据为例，待检测目标是直径1 m的漂浮圆球，其外表被金属丝所包裹，处于15 m×30 m的距离分辨单元内。由于雷达以小擦地角方式照射海域，漂浮圆球的起伏会导致雷达回波信号能量的扩散，使得目标单元临近距离单元受到影响而成为受目标影响单元。对于320#数据来说，目标位于7号距离单元，6、8、9号为受目标影响单元，其余为杂波单元。

经过特征空间转换，IPIX实验320#数据复相关相位斜率矩阵KIPIX的幅度如图6所示。

图6 复相关相位斜率矩阵

图6为复相关相位斜率矩阵KIPIX幅度的三维展示，从中可以看出复相关相位斜率矩阵KIPIX中目标单元与杂波单元差异性十分显著。

利用目标单元与杂波单元复相关相位斜率幅值的差异性可进行判别门限设置：

(2)

式中：Ks和Kc分别为目标和海杂波单元的复相关相位斜率；H为检测结果；η为判别门限。

3 目标检测方法性能评估

为验证本文提出的基于复相关相位斜率特征的目标检测方法的有效性，将其与时域Hurst指数检测方法进行对比。

时域Hurst指数检测器在现有雷达信号处理研究中比较流行，多尺度Hurst指数可以简单描述海杂波时间序列在不同尺度上的粗糙程度，如果在多个尺度上的Hurst指数相同，则意味着海杂波序列在不同尺度上具有相近似的粗糙程度，该扩展自相似过程就退化为自相似过程，可用Hurst指数来完全描述，例如分形布朗运动。

海杂波信号并不是理想的分形体，其分形特征只能在一定尺度区间内得以体现。对于IPIX雷达实验数据而言，经过大量实验[6,12]证明，其海杂波时域信号的FRFT域分形的无标度区间为4～12尺度。

本文中利用小波分析中的方差法提取IPIX雷达实验320#数据时域信号的Hurst指数，并与雷达信号的复相关相位斜率特征进行对比，对比结果如图7所示。图7中给出了VV极化和HH极化方式下的各距离单元Hurst指数和复相关相位斜率均值。

图7 目标检测性能对比

对于Hurst指数计算结果，可以看出：

(1)目标单元的Hurst指数高于杂波单元的Hurst指数，Hurst指数具备一定的能力来区分杂波与目标。

(2)Hurst指数受信杂比影响严重，VV极化下的雷达信号的信杂比很低，导致杂波单元Hurst指数最大值与目标单元Hurst指数的差值较小，这就限制了目标检测方法中判别门限的选择范围及目标检测概率。

(3)不同杂波单元的Hurst指数差别较大，尤其是在VV极化方式下。

而从复相关相位斜率均值计算结果中可以看出：

(1)目标单元与杂波单元的复相关相位斜率均值差距较大，给目标检测方法中判别门限提供了选择空间。

(2)在不同极化方式下，目标单元与杂波单元的复相关相位斜率均值都有较大差异。

(3)不同杂波单元的复相关相位斜率均值之间较为均衡，稳定在相对固定的区间之内，这可以很大程度上减低虚警概率，而且十分有助于海杂波抑制方法研究。

接下来定量对比复相关相位斜率特征与时域Hurst指数检测方法，我们将检测结果在杂波最大值、杂波标准差、目标值及差值等方面进行对比(见表1)。

表1 检测结果对比

从表1可以看出，在不同极化方式下，目标单元与杂波单元复相关相位斜率特征的差值都大于其Hurst指数的差值，这说明利用复相关相位斜率特征比Hurst检测方法更容易识别海面弱小目标，尤其是在低信杂比条件(VV极化方式)下，复相关相位斜率特征的优势更明显。对于不同海洋环境参数下的低信杂比雷达数据，复相关相位斜率特征的优势同样存在(见表2)。

表2 IPIX雷达数据检测结果对比

假设以图7b中目标与杂波单元复相关相位斜率的均值作为判别门限，则320#数据在HH极化方式下的检测概率为96.48%，即便信杂比较低的VV极化方式，检测概率也可达88.67%，从而证明了该方法的有效性。

4 结语

针对海杂波严重制约雷达目标探测性能的问题，本文提出了一种基于复相关相位斜率特征的海面弱小目标检测方法。

首先，通过研究海杂波复数域下的时间自相关特性，发现了海杂波复相关系数的相位信息呈线性分布，并由此提出了复相关相位斜率特征的概念。研究表明，复相关相位斜率特征可显著提高雷达数据的信杂比。

然后，本文设计了一种基于复相关相位斜率特征的目标检测方法，其核心在于特征空间转换。通过将雷达数据由幅度空间转换到复相关相位斜率空间，目标单元的可检测性显著提高。

最后，利用不同极化方式实测的雷达数据对目标检测性能进行评估。结果表明，目标单元与杂波单元复相关相位斜率特征的差值明显大于其Hurst指数的差值。这说明利用复相关相位斜率特征比传统时域Hurst检测方法更容易识别海面弱小目标，尤其是在低信杂比条件下，复相关相位斜率特征的优势更加明显。

本文只是利用了复相关系数的相位特征来进行目标检测方法研究，目的在于证明复相关相位斜率特征应用于目标检测方法研究的可行性。未来，可以尝试结合其他多种统计特征，建立联合特征矩阵，利用机器学习方法来进一步提高目标检测方法的性能，这将是十分有潜力的研究方向，值得关注。