水平荷载下基于桩-土相互作用的定位桩承载能力

， ， ，

(1.中国舰船研究设计中心，武汉 430064；2.上海交通大学 高新船舶与深海开发装备协同创新中心， 上海 200240；3. 上海交大海洋水下工程科学研究院有限公司， 上海 200231；4. 中国铁建港航局集团有限公司， 广东 珠海519070)

水平荷载下基于桩-土相互作用的定位桩承载能力

陶鹏1，2，杨启2，3，程旭东4，金晔4

(1.中国舰船研究设计中心，武汉430064；2.上海交通大学高新船舶与深海开发装备协同创新中心，上海200240；3.上海交大海洋水下工程科学研究院有限公司，上海200231；4.中国铁建港航局集团有限公司，广东珠海519070)

研究挖泥船定位桩在桩顶水平载荷下的承载特性，引入p-y曲线描述桩-土界面的非线性接触，分别基于连续算法及微元法建立桩-土相互作用下的定位桩 “梁”力学模型，对其桩身内力及位移分布进行探讨。实例表明，桩细长比、土体特性以及桩基深度等对定位桩承载能力都有较大的影响。在作业区域土体性质确定的情况下，可通过增加桩径及定位桩插桩深度来提高定位桩水平极限承载能力。

水平载荷；定位桩；桩-土分析；承载能力；p-y曲线

0 引 言

定位桩是保证海洋疏浚工程的超大型桩定位挖泥船正常作业的关键部件。抓斗船在进行插桩作业时，环境载荷与工作载荷直接作用于船舶主体，最终由定位桩承受并传至海底[1]。这种定位桩一般都插深较小且具有较长的土体外露段，而钢桩整体的刚度值远小于船舶主体。为保证船体正常作业及定位桩结构的安全性，定位桩主要用于限制船体水平方向的运动，而对于船体摇摆及升沉运动不直接进行控制。在挖泥船定位桩结构设计中，传统做法大多将土体对定位桩的约束作用简化为绞支座或弹性固定端，对土体承载机理的研究不足，计算精度难以保证。因此，寻求更为有效的桩-土相互作用处理方式对于挖泥船定位桩的结构设计具有较大意义。

在理论研究方面，目前对于定位桩结构响应中的桩-土相互作用问题的处理方式[2-6]主要有3种：(1)将泥土对于桩基的约束作用看成弹性固定端。该方法最简单，但计算精度难以保证。(2)基于地基反应力法(土弹簧法)模拟泥土对于钢桩的约束作用，将泥土离散为一个个独立的弹簧。根据对土的侧向抗力系数的不同考虑，有K法、m法及p-y曲线法等，计算精度较第1种有所提高，而难点在于土体参数与弹簧刚度系数的获取。(3)利用非线性有限元软件模拟桩-土之间的相互作用，并采用接触算法。软件内大多内置有可供选择的土体本构模型，可以保证较高的计算精度，但这与有限元网格如何划分等有很大关联，需要较高的软、硬件资源。

在试验研究方面，DAVISSON等[7]于1975年在标准沙中用铝合金管模拟水平荷载作用下的桩，并进行模型试验，结果表明：循环载荷及桩基深度等对于单、群桩的弯曲行为有较大影响。ISMAEL[8]对中等密实砂浆中单桩和群桩的水平承载特性进行模型试验，并提出砂浆中水平受载桩的非线性受力特点。DYSON等[9]使用离心机对砂土中的水平受载桩进行模拟，提出在桩-土相互作用过程中需分开处理钙质沉积物与其他土壤类型，并得到较理想的试验结果。在国内，韩理安等[10]根据多年的现场试桩资料提出一种非线性计算方法，并采用相似理论方法构造出一种新的p-y曲线，称作NL法。

为充分考虑挖泥船定位桩桩-土间接触的非线性问题，并进一步揭示钢桩细长比、插桩深度及土体参数等对定位桩水平承载能力的影响。本文采用p-y曲线描述定位桩桩-土接触特性，并根据水平荷载下的桩身受力平衡方程和“梁”结构分析法等对该类定位桩的承载特性及桩身内力、位移分布等进行研究。

1 桩-土界面接触模型与水平承载桩受力特性

1.1桩-土接触面模型

在设计挖泥船定位桩时，为充分考虑定位桩桩-土相互作用的非线性特性，采用弹性地基反力法即p-y曲线法。p-y曲线是一种弹塑性方法，能综合反映桩周土的非线性、外载荷作用特性及由地表开始的渐进性破坏现象。图1a)为挖泥船定位桩，它通常插深较小且具有较长的土体外露段，对定位桩及其桩周土体承载特性的详细研究，将决定其在桩顶水平载荷F下能否保证挖泥船定位精度，并能改进定位桩结构设计。

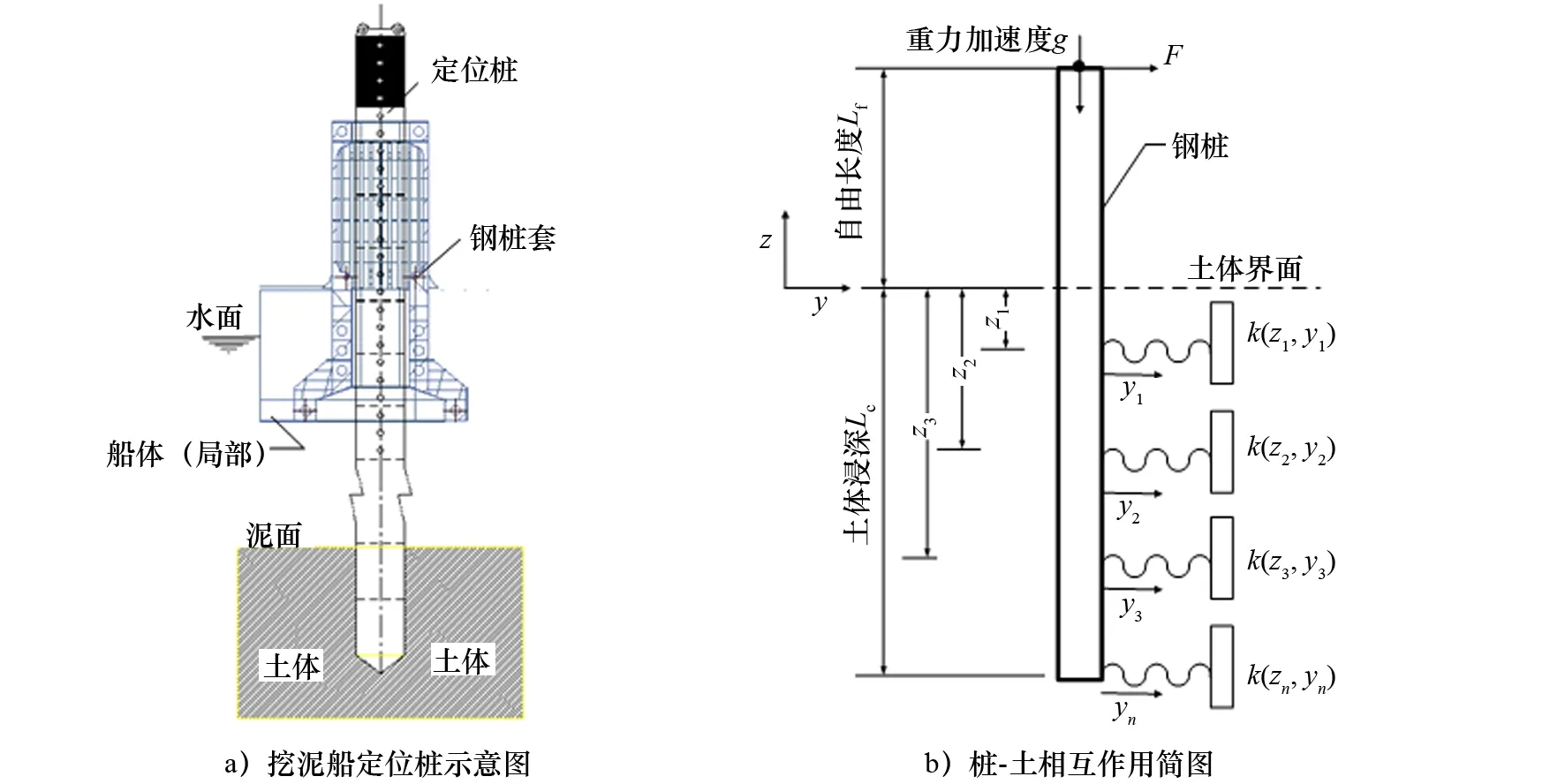
图1 定位桩桩-土相互作用简化

在定位桩泥面以下建立p-y曲线桩-土简化模型[11]，如图1b)所示。钢桩为等截面圆管钢质摩擦承载桩，土体分层设置有p-y曲线型土弹簧。需确定不同深度相对应的p-y曲线。p-y曲线法基本表达式[11]为

式中：P(z,y)为z处土体侧向位移为y时的土抗力，即桩-土相互作用力；k(z,y)为土抗力系数即弹簧刚度系数；be为桩的计算宽度(与桩径有关)。

1.2钢桩侧向力分布

参考相关数值试验结果[2-6]，在同类型钢桩桩顶作用某一水平载荷F时，其侧向位移在泥面以下满足如下分布规律：(1)在泥面处取得最大值，该处土体通常也是最先发生破坏的地方。(2)随着桩基深度值加大，其侧向位移(与载荷同向)逐渐减小，直至某一临界深度时变为0；当桩基深度值进一步加大时，钢桩出现较小的反向位移。按桩基临界深度将土体分为上层与下层土体，其交界处节点记为“位移零点”M。如图2所示。

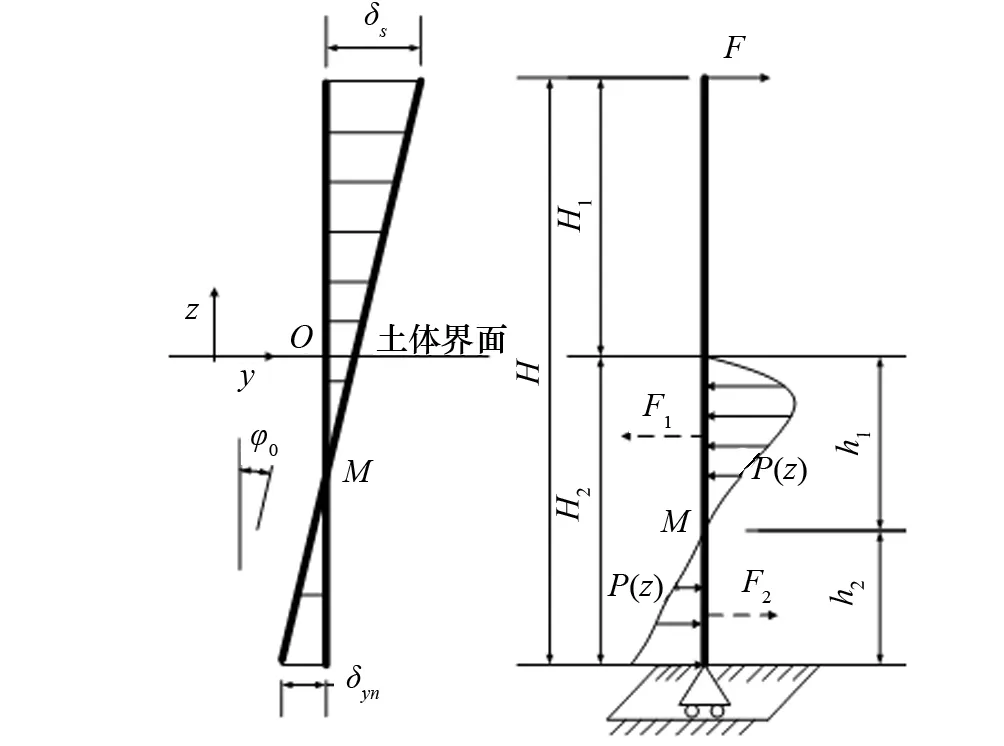
图2 定位桩桩-土力学模型

由于土体土抗力与其侧向位移在土体破坏前一般呈正相关，根据作业精度要求，挖泥船会允许一定的水平位移， 即定位柱桩顶位移(为分析方便，在某一插桩深度H2下假定位移为δs)。在挖泥船作业工况下，可根据船体外载荷确定桩顶水平载荷F。由于挖泥船定位桩大多为浅插深桩，且钢桩的自身刚度值明显大于浅层土体，在钢桩小角度倾斜时，初步假定钢桩是完全刚性的，此时钢桩绕位移零点M的倾斜转角记为钢桩刚性转角φ0。运用梁分析方法推导出定位桩在泥面以下的侧向力分布与桩基位移零点的位置。

图2为定位桩梁力学模型，假设定位桩侧向位移在泥面以下h1处为零。在泥面处建立yOz直角坐标系，z方向垂直泥面向上，坐标系原点取为钢桩垂直位置与泥面相交处，桩身(泥面以下)初始位移分布为

将δy代入土抗力系数k，并沿桩身积分，确定土体的土抗力为

式中：F1为上层土体土抗力；F2为下层土体土抗力；Crz为桩基z位置处截面桩-土接触带周长。

以定位桩桩基“位移零点”M为基准建立平衡方程：

式中：l1为F1到M的作用力臂；l2为F2到M的作用力臂；G为钢桩自重，完全由土体侧向摩擦力平衡，钢桩重心约位于钢桩长度H/2位置处；由于φ0一般不会太大，式(5)中sinφ0项基本为零。

综上，可确定h1与h2(可得插桩深度H2)，从而求得桩基侧向力及桩身内力分布。

2 桩身内力与位移分析方法

将钢桩等效为悬臂梁，如图2所示，对钢桩内力(弯矩、剪力)及位移分布进行计算。定位桩主要受到桩顶水平载荷及土体反力的作用，钢桩重力及土体侧向摩擦力对桩身弯矩及剪力分布的影响可以忽略不计。为分析方便，将桩身坐标系原点移至桩顶。

(1) 桩身剪力及弯矩分布:

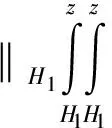
式中：P(z)为z(z>H1)处土抗力密度(离散值)；N(z)为桩身剪力函数；M(z)为桩身弯矩函数；Hni为桩身第ni个单元的垂向坐标。

(2) 定位桩合成应力为

式中：Gz为钢桩在z位置以上钢桩自重；Az为z位置处钢桩截面面积；Kz为钢桩桩基z位置以上所受到的土体侧向摩擦力，与土抗力成正比；μ为侧向土体摩擦力系数。

3 定位桩力学模型的应用

3.1钢桩模型介绍

当钢桩插桩深度H2一定时，根据第1节可确定钢桩位移零点M与桩顶位移δs。由于钢桩与土体弹性模量相差较大，在钢桩侧向位移分量中δy≪ye。本文通过实例研究钢桩承载能力，即桩顶载荷F与其刚性转角φ之间的规律，并考虑钢桩直径的影响，钢桩基本参数设置见表1。定位桩为金属钢桩，内敷设骨材。

表1 钢桩基本参数设置

3.2土体参数计算

由于挖泥船作业区域浅层土体大多为硬质砂土，参考文献[12]，确定各直径钢桩在砂土中的p-y曲线数据。砂土极限土抗力转折点深度[12]满足：

式中：zr为极限土抗力转择点深度；C1,C2,C3为已知系数；d为桩径或桩宽。

土体参数的设置情况见表2，由于定位桩桩基位移零点大多靠近桩底，为分析方便，假定位移零点始终位于桩底。

表2 土体参数设置

单位桩长的极限水平土抗力标准值[12]为

砂土中的p-y曲线[12]为

式中：P为泥面以下Z位置单位桩长的水平土抗力标准值；ψ为计算系数；K为土抗力初始模量；Z为泥面以下桩基某一深度；y为泥面以下Z深度处桩的侧向位移。

根据式(10)可确定定位桩在砂土中给定深度处的p-y曲线，各钢桩直径p-y曲线结果如图3～图5所示。钢桩直径3 m时各桩深水平土抗力计算函数见表3。

表3 钢桩直径为3 m时的p-y曲线函数

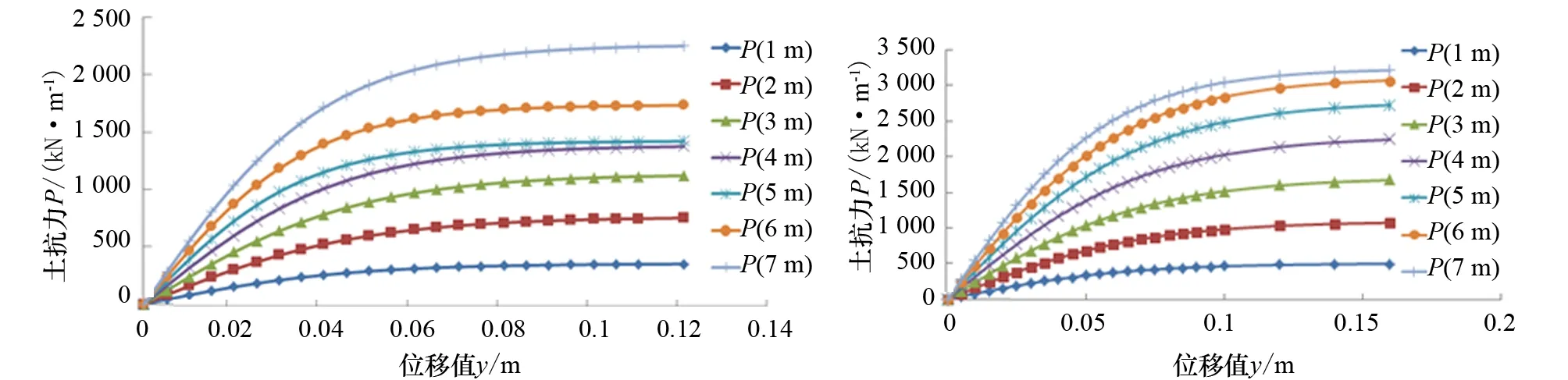
图3 钢桩直径为2 m时各桩深p-y曲线 图4 钢桩直径为3 m时各桩深p-y曲线

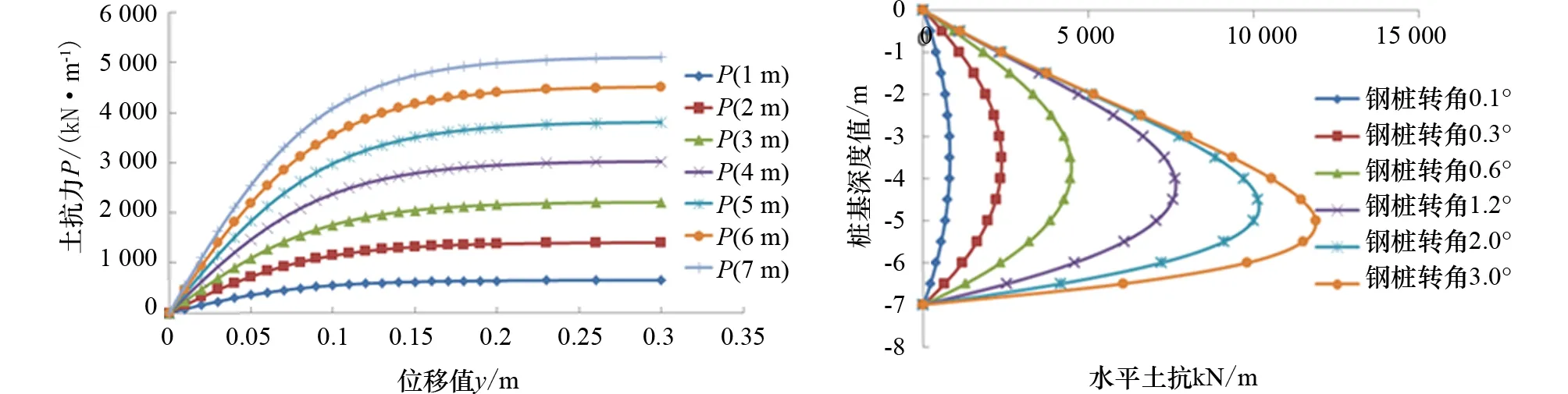
图5 钢桩直径为4 m时各桩深p-y曲线 图6 钢桩直径为4 m时各桩深承载特性

为更好评估桩周土体承载特性，对各桩深土体承载能力进行计算(直径4 m)，结果如图7所示，可以看出：(1)在同等条件下，钢桩直径越大，各桩深处土体的土抗力极值越大，达到土抗力极值时的横向位移值有所增大；(2)同一桩深处，土抗力随着土体侧向位移变大而逐渐增大，并快速进入缓和段直至土抗力极值。

3.3定位桩承载能力参数化研究

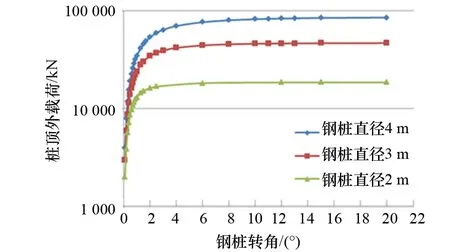
图7 各直径钢桩F-φ承载曲线

图7为定位桩桩顶水平外载F(即定位桩承载能力)与其刚性转角φ之间的关系曲线，不同定位桩直径还需考虑接触带周长的影响。

在插桩深度一定的情况下，土体所能承受的极限桩顶水平载荷不超过桩基位移零k点以上土体的极限土抗力总和。以钢桩直径3 m时为例，本例中土体所能承受的极限桩顶载荷约为45 181 kN，此时钢桩刚性转角φmax约为8°。在实际情况下，桩基位移零点M会稍高于桩底，随着φ的增大，位移零点会向下移动并靠近桩底，桩周土体所能承受的极限桩顶载荷F会有所增大。在同等条件下，土体所能承受的极限桩顶载荷与钢桩直径成正比。

3.4桩身位移及应力分布

以定位桩直径3 m时为例，如果其桩顶作用载荷为6 000 kN (设计载荷)，则钢桩刚性转角为0.203°，此时定位桩桩顶位移约为0.15 m，能够满足挖泥船桩作业精度要求。图8为定位桩在泥面以下转动位移值、弹性修正位移值及实际位移值的桩身分布曲线，可以看出：与钢桩转动位移相比，其弹性修正位移几乎可忽略不计，这也表明了上述假定(钢桩作刚性转动)在一定情况下是满足精度要求的。

由于钢桩自重与土体侧向摩擦力引起的轴向压缩作用，选取钢桩截面受压一侧最大应力值进行计算，图9为定位桩泥面以下弯曲应力值与其合成应力值的桩身分布情况。定位桩弯曲应力在合成应力值中占主要成分，本例桩身最大应力值约为85 MPa，其位置靠近位移零点。

图8 桩身位移值分布曲线(泥面以下) 图9 桩身应力值分布(泥面以下)

4 结论

本文综合考虑挖泥船定位桩承载特点及其桩土相互作用特性，引入p-y曲线描述桩-土的非线性接触，运用“梁”分析方法探讨钢桩在桩顶水平载荷下的受力特性，并对桩身位移及内力分布也进行了相关研究，主要得出以下结论：

(1) 本文所建立的定位桩梁力学模型综合考虑定位桩受力特性与桩-土接触非线性，能够很好地辅助挖泥船定位桩初步设计工作，评估定位桩承载能力及其结构强度状态。

(2) 实例分析表明，土体主要承载区域靠近桩基位移零点，定位桩结构设计时应注意对该区域进行适当加强，如适当增大定位桩局部区域壁厚或增设内骨材等。

(3) 钢桩承载能力与钢桩细长比、桩基深度、土体特性等都有很大关联，作业区域土体性质确定条件下，可通过适当增加桩径与定位桩插桩深度来提高定位桩水平极限承载能力。

[ 1 ] 李竹森，罗君文. 钢桩式抓斗挖泥船施工流程分析[J]. 装备制造技术，2014 (03)：237-239.

[ 2 ] 孙希. 海上风电基础结构桩-土相互作用研究[D]. 青岛：中国海洋大学，2014.

[ 3 ] 张兴其. 桩-土相互作用的接触分析研究与应用[D]. 南京：河海大学，2007.

[ 4 ] 李强. 基于桩-土相互作用的自升式平台桩靴强度研究[D]. 大连：大连理工大学，2008.

[ 5 ] 朱照清，龚维明，戴国亮. 大直径钢管桩水平承载力现场试验研究[J]. 建筑科学学报，2010, 26(09): 36-39.

[ 6 ] 胡翔，陈锦剑. 波浪荷载下海底单桩与土共同作用的数值分析[J]. 岩土工程学报，2015, 37(02): 217-221.

[ 7 ] DAVISSON M T, SALLY J R. Model Study of Laterally Loaded Pile[J]. SMF Div, ASCE, 1970, 96(05)：1605-1620.

[ 8 ] ISMAEL N F. Behavior of Laterally Loaded Bored Piles in Cemented Sands[J]. Geotechnical Engineering, ASCE, 1990, 116(11): 1678-1699.

[ 9 ] DYSON G J, RANDOLPH M F. Monotonic Lateral Loading of Piles in Calcareous Sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(04): 346-352.

[10] 韩理安. 群桩水平承载力的实用计算[J]. 岩土工程学报，1986, 8(03): 23-36.

[11] 赵明华，邬龙刚，刘建华. 基于p-y 曲线法的承重阻滑桩内力及位移分析[J]. 岩石力学与工程学报, 2007, 26(06): 1220-1226.

[12] 中国交通运输部. 港口工程桩基规范[M]. 北京．人民交通出版社，2012

BearingCapacitiesofPositioningPileUnderLateralLoadsBasedonPile-SoilInteraction

TAO Peng1，2，YANG Qi2,3，CHEN Xudong4，JIN Ye4

(1.China Ship Development and Design Center, Wuhan 430064， Hubei, China; 2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China; 3. Shanghai Jiao Tong University Underwater Engineering Institute Co., Ltd., Shanghai 200231, China; 4. China Railway Port Bureau Group Co., Ltd., Zhuhai 519070, Guangdong, China)

Bearing properties of the positioning pile under lateral load is studied, and the p-y curve is introduced to describe the nonlinear contact interface between pile and soil. The beam mechanical model of positioning pile considering pile-soil interaction is presented based on continuation algorithm and differential method respectively. Both of the inner-force and displacement distribution of pile are discussed. The examples show that the slenderness ratio of pile, the soil characteristics and the depth of pile foundation have great influence on bearing capacity of positioning pile. With the soil type determined in the working area, the horizontal ultimate bearing capacity of the positioning pile can be improved by increasing the diameter of pile and the depth of pile foundation.

lateral load; positioning pile; pile-soil analysis; bearing capacity; p-y curve

U616

A

2016-06-13

工信部高技术船舶科研计划项目(工信部联装[2012]539号),国家自然科学基金项目(51179104)

陶 鹏(1991-)，男，硕士研究生

1001-4500(2017)05-0055-07