窄条翼布局导弹摇滚特性及流动机理

冯黎明， 达兴亚， 吴军强， 赵忠良

中国空气动力研究与发展中心 高速空气动力研究所， 绵阳 621000

窄条翼布局导弹摇滚特性及流动机理

冯黎明*， 达兴亚， 吴军强， 赵忠良

中国空气动力研究与发展中心 高速空气动力研究所， 绵阳 621000

钝头体窄条翼布局导弹在大攻角下拥有极为优异的纵向气动特性，但横向容易失稳，做快速机动时容易诱发非指令的横向不稳定运动。通过开展高速风洞自由摇滚试验和数值模拟，研究了窄条翼导弹自由摇滚特性和流动机理，试验与计算吻合较好。研究发现：较大迎角时，窄条翼面积中心距离尾舵前缘根部5～6倍直径时，模型会进入极限环摇滚，窄条翼位置对模型稳定性有显著的影响，去掉窄条翼或尾舵时，模型均不会进入摇滚；模型空间流场特性表明，气流经过窄条翼时形成的片涡，对背风舵产生强烈的干扰，抑制了尾舵涡的形成和发展，使背风舵动态失稳，导致模型进入极限环摇滚。

窄条翼； 导弹； 极限环摇滚； 动态； 流动干扰

“摇滚”是飞行器滚转方向的自激振荡，通常以极限环振荡形式出现[1-3]，摇滚运动在一个周期内运动吸收的能量等于耗散的能量，形成等幅等周期振荡[4-9]。传统导弹的布局形式相对简单，飞行迎角不大，摇滚问题不突出。研究主要集中在机翼摇滚，例如，国内外对典型三角翼摇滚开展了大量研究[10-12]。已有文献表明，摇滚运动特性与飞行器布局密切相关[13-14]，不同构型的摇滚运动机理差别很大。所以机翼摇滚的研究成果很难直接应用于细长体外形布局的导弹上，孙海生[14]在研究战斗机摇滚特性时，观察到了单独机身的摇滚现象，因此刘伟等[15]指出，现代导弹也应进行摇滚运动的研究。

窄条翼布局是高机动战术导弹采用的一种典型布局形式，其特点是在弹身中后部和尾舵的正前方布置极小展弦比窄条翼[16]。这种布局导弹纵向气动特性极为优异，在大迎角范围内(60°)法向力保持单调递增，但由于窄条翼和舵之间强烈的流动干扰，导致导弹横向气动特性非常复杂，导弹在做快速机动时，容易诱发滚转方向不稳定的运动。目前，还不清楚亚、跨声速范围内该类布局导弹的摇滚特性，更缺乏对摇滚运动产生机理的认识。因此迫切需求开展这方面的研究，能够给导弹飞行控制系统提供理论支撑。

小展弦比导弹的滚转气动阻尼相对很小，动态试验中轴承摩擦阻尼等干扰因素对摇滚特性具有显著的影响，目前也没有一种普适的修正方法，造成试验系统误差偏大的困难；摇滚数值模拟涉及气动和运动耦合问题，对耦合求解策略和计算任务量提出了很高的要求。本文拟在气动和运动高阶紧耦合计算方法的基础上，开展数值模拟，结合高速风洞自由摇滚试验，搞清窄条翼布局导弹自由摇滚特性，挖掘气动/运动耦合特性和摇滚运动产生的流动机理。

1 自由摇滚数值模拟方法

1.1 流场主控方程

研究对象属于三维非定常湍流流动，一般采用三维可压缩非定常雷诺平均Navier-Stokes方程[17]，在贴体坐标系(ξ，η，ζ)可写为

(1)

式中：Q为守恒变量；F、G和H为无黏通量；Fv、Gv和Hv为黏性通量；t为时间。

1.2 飞行力学方程

弹体坐标系里导弹绕质心转动的动力学方程为[18]

(2)

运动学方程为

(3)

式中：ϑ、ψ和γ分别为导弹俯仰、偏航和滚转角；I为转动惯量；M为力矩；ω为角速度。

1.3 数值模拟方法

流场求解采用基于结构网格的有限体积法，时间推进采用双时间步法[19]，黏性项采用Jameson中心差分，无黏项采用Roe格式[20]，使用Venkat限制器，湍流模型采用Spalart-Allmaras模型。气动/运动耦合策略采用了文献[21]中提到的三阶Adams紧耦合方法，在保证一定的精度和流场收敛的前提下，能显著减小计算任务量。

2 自由摇滚高速风洞试验

2.1 设备和模型

试验在中国空气动力研究与发展中心高速空气动力研究所1.2 m×1.2 m跨超声速风洞中进行。

试验模型为钝头体、窄条翼和梯形尾舵布局导弹，如图1中所示，模型弹径D=42 mm，全长L=19D，窄条翼根部长6D，窄条翼面积中心距弹头顶点11D，将该状态定义为基本状态模型。0° 迎角时的堵塞度约0.1%。摇滚特性通常用平均滚转角γ0，(°)、滚转角均方根σγ、频率f,Hz和振幅φ，(°)来表征。

平均滚转角：

(4)

滚转角均方根：

(5)

图1 窄条翼布局导弹外形
Fig.1 Shape of missile with strake wings

2.2 结果及讨论

图2 模型自由摇滚时间历程
Fig.2 History of free roll angle of model

试验马赫数Ma=0.6，迎角α范围为7°～40°，图2中给出了基本状态模型自由摇滚时间历程曲线。定义模型在滚转角等于0° 时，处于“×”字布局。模型在迎角为7°～15° 时稳定在“十”字布局；在15°～20° 之间转向“×”字布局；在20°～30° 时模型基本稳定在“×”字布局，但平衡滚转角与对称状态略有偏差，同时伴有微振，以25° 最为明显；在35°时模型形成“×”字布局准极限环摇滚，平均滚转角γ0=1.35°，频率f=13 Hz，滚转角均方根σγ=11.3°，振幅φ=16°；在40°迎角时，平均滚转角γ0=0.73°，频率f=14 Hz，滚转角均方根σγ=8.9°，振幅φ=12.6°。可见，基本状态模型随着迎角增大，先从“十”字稳定过渡到“×”字稳定，然后在35° 迎角出现摇滚，且摇滚的振幅随迎角增大而减小，频率基本保持不变。

在基本模型状态基础上，去掉窄条翼或尾舵时，模型均基本稳定在0°附近，即模型只有单独窄条翼或尾舵时不会发生摇滚。

3 自由摇滚数值模拟

3.1 基本状态自由摇滚特性

首先计算基本状态模型，图3中给出了模型计算网格。网格采用标准多块对接形式，弹身周向分布了223个网格点，将尾舵流向方向的网格进行了加密，网格总量约500万，其上游距头部10L，下游距后缘10L，远场边界距中心线7L。为提高并行计算效率，将网格分为140个块，保证每个计算核心分配到大致相等的计算量。使用了三重“W”型多重网格。

计算时，在平均滚转角γ0和初始角速度等于0的状态下启动。计算条件为：Ma=0.6，来流密度为1.225 kg/m3，基于弹径的雷诺数ReD=1×106，转动惯量为0.001 kg·m，计算迎角α=30°～40°；物理时间步长取0.001 s；导弹在初始滚转角释放。

表1中给出了不同迎角下的计算结果。当迎角小于35°时，模型处于动稳定，最终稳定在平衡滚转角处；当迎角增大到36°～40°时，模型进入极限环摇滚。迎角进一步增大时，气动力作用下极限环开始不稳定，出现连续翻滚等复杂的动态运动特性。

图3 模型计算网格
Fig.3 Computational grids of model

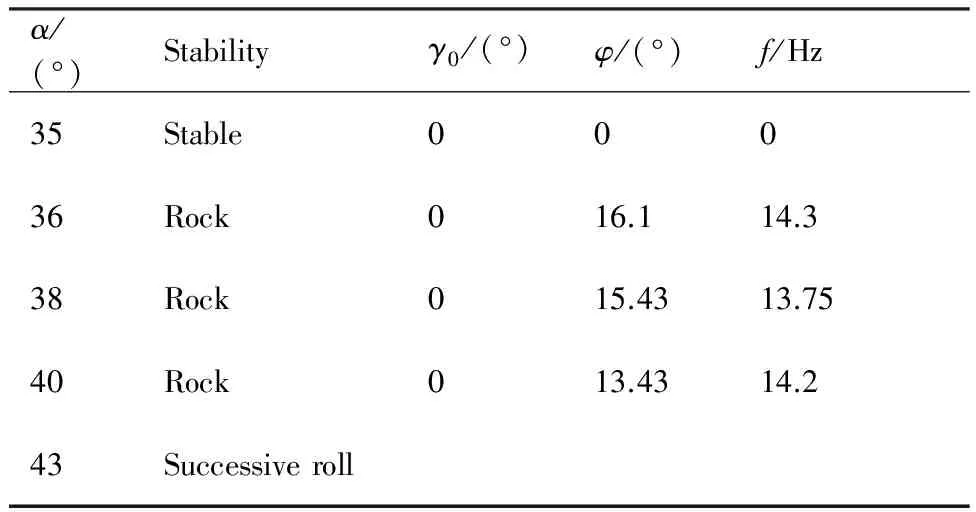
表1 基本状态模型仿真结果Table 1 Simulation results of basic model

图4中给出了α=35°、36° 时的摇滚特性曲线。Cmx为滚转力矩系数，α=35° 时，模型从γ= -5° 开始释放，滚转振幅一直在衰减，直到最终稳定在γ=0° 处；α=36° 时，滚转力矩随滚转角的迟滞曲线呈双“8”形，模型进入极限环摇滚，相图中前一个周期和下一个周期完全重合，摇滚振幅为16.1°，频率为14.3 Hz；此状态的风洞试验振幅为16°，频率为14 Hz。数值模拟与试验基本吻合。

图4 摇滚运动特性
Fig.4 Rock motion characteristics

3.2 窄条翼和尾舵对摇滚特性的影响

对去掉全部窄条翼(No strake wings)或去掉全部尾舵(No tailfins)状态进行了数值模拟，计算得到的结果均是动态稳定的，即如果弹体上只有窄条翼或只有尾舵时，导弹均不会进入极限环摇滚，这一结果与试验结果一致，也从侧面说明窄条翼和尾舵之间存在强烈的流动干扰，对导弹摇滚特性有显著影响。

3.3 窄条翼位置对摇滚特性的影响

以基本状态模型的窄条翼位置为基准，远离尾舵的方向移动D，记作Strake+D，靠近尾舵的方向移动D，记作Strake-D，表2中给出了计算结果，只有Strake-D模型进入了极限环摇滚，且摇滚起始迎角提前到33°，振幅相对于基本状态显著增大，即动不稳定性增强了；同时，Strake+D模型动态稳定，这一结论进一步验证了窄条翼与尾舵的干扰特性，且作用强度随距离的减小而增强。第4节将详细讨论摇滚中窄条翼与尾舵之间的干扰。

表2 不同窄条翼位置模型仿真结果

4 窄条翼导弹摇滚的流动机理分析

4.1 部件稳定性分析

以基本状态模型在迎角等于36°的状态为例，由于模型的轴对称性，可将模型分解为弹体、迎风和背风窄条翼以及迎风和背风尾舵。计算时，利用网格分块可以很方便的对某一块物面区域单独积分，输出气动力和力矩等。图5中给出了部件滚转力矩迟滞曲线。

弹身的迟滞环面积几乎等于0，处于中立动稳定；迎风和背风窄条翼的迟滞环都是逆时针，处于动稳定；迎风尾舵和背风尾舵迟滞环都是顺时针，处于动不稳定，但背风尾舵的迟滞环面积相对比迎风尾舵大很多。背风尾舵在平衡滚转角附近迟滞环面积非常大，在两头相对较小，窄条翼则分布比较均匀。结合前面的窄条翼对模型尾舵动稳定性影响的结论，可以直观地得到摇滚运动的动力特性：

1) 在小滚转角范围，由于窄条翼产生的动稳定性不足以抵消背风尾舵产生的动不稳定性，模型整体会吸收能量，导致了模型在滚转方向的运动发散。

图5 部件滚转力矩迟滞曲线
Fig.5 Roll moment time-lag of part

2) 当滚转角逐渐增大，背风尾舵的动不稳定性逐渐减弱(对应图中迟滞环缩小)，在“8”字环交叉点后模型又重新进入动稳定状态，此后模型不断耗散能量，角速度开始减小。

3) 在最大滚转角处，模型的动能被全部耗散，速度减小到零，在尾舵的静态滚转力矩(窄条翼和弹身提供的滚转力矩很小)作用下，模型重新开始向平衡点加速。

4) 在从最大滚转角向平衡点加速的过程中，尾舵依然在吸收能量，但吸收的能量不足以抵消窄条翼耗散的能量，模型处于动稳定，经过“8”字环交叉点后模型又重新进入动不稳定状态，模型吸收能量加速经过平衡位置。

4.2 窄条翼对尾舵的流场干扰分析

4.2.1 静态干扰

首先对基本状态模型开展了静态数值模拟，图6中给出了在迎角为36°时有/无窄条翼模型的流线和压力云图。

对于窄条翼导弹，较大迎角时涡系对导弹气动特性有着至关重要的影响，因此有必要对涡系的形成、发展和相互作用的过程开展详细的研究，图6 中分别给出了基本状态模型和去窄条翼模型，在迎角等于36°时的静态流场特性，Cp为压力系数，观察方向为由后向前。

从图6所示的基本状态模型流线图可以看出，气流向下游运动，在到达x/L=0.2截面时已经分离(记作前体涡)，并在模型表面诱导分离出二次涡；当气流到达窄条翼后，前体涡已经飘得很高，并从窄条翼上方掠过，同时吸收了背风面窄条翼上方产生的涡量。上下窄条翼之间由于气流受阻，黏性作用增大，产生了一对新的分离涡(记作片涡)，但受背风窄条翼的影响，空间发展受到制约。气流经过窄条翼之后，在x/L=0.75 截面，由于片涡不再受窄条翼阻挡，逐渐抬高，又受到主流的横向挤压，最后与前体涡合并。到达x/L=0.85时，已经合并成了一对新的自由涡(依然将其称作片涡)。气流到达尾舵截面x/L=0.91时，形成了一对远离背风舵、高高飘起的自由涡，上下尾舵之间产生了一对分离涡，但背风面没有产生新的涡，这与窄条翼截面的流场结构具有相似性。

无窄条翼的情况下(图6(b))，分离涡结构在尾舵附近发生了显著的变化。无窄条翼时前体涡向下游发展，不断吸收弹身表面产生的涡量，导致前体涡一直贴近弹体，同时保持较高的强度。到达x/L=0.91时，前体涡依然保持较低的高度，此时背风舵也产生了分离涡(在x/L=0.95清晰可见)。尾舵涡的产生也导致背风舵表面形成了大面积的低压区。显然带窄条翼模型背风舵上下表面压差小很多，使得舵面横向稳定性减弱。

以上静态流场分析表明，窄条翼片涡对背风尾舵的影响最大，直接导致背风舵表面不再产生尾舵涡，从而减弱了导弹的横向稳定性。这与前文力矩迟滞曲线得到的结论是一致的。

图6 不同截面静态流线及压力分布
Fig.6 Steady streamline and pressure distribution of different sections

4.2.2 动态干扰

图7给出了基本状态模型在迎角等于36°、极限环摇滚时，一个周期内窄条翼和尾舵截面的流场特性。

在模型顺时针经过0°时(ω>0，图7(a))，尾舵上方左涡接近舵面，而右涡高高飘起，这直接导致了左侧背风舵表面产生很大的压差，形成顺时针的滚转力矩(力矩大于0)，而右侧背风舵的压差相对小很多，所以背风舵总体产生了顺时针滚转力矩。在模型逆时针经过0°时(ω<0，图7(c))，涡结构刚好相反，进而导致背风舵产生逆时针滚转力矩(力矩小于0)。可见，模型处于平衡滚转角附近时，背风舵总是会产生使模型偏离平衡位置的力矩，即模型动不稳定。模型顺时针到达极限位置16.1° 时(ω>0，图7(b))，右侧尾舵背风面上方压力呈负值，产生逆时针滚转力矩，当模型逆时针到达极限位置-16.1° 时(ω>0，图7(d))，则在左侧尾舵背风形成低压区，产生顺时针滚转力矩。极限位置时，力矩会阻止模型偏离平衡点，模型又处于动稳定。

对于无窄条翼模型，由于自由涡靠近弹体表面，很难像带窄条翼模型那样使自由涡在空间非对称运动，因此也就没有进入摇滚。

图7 截面流线及压力云图
Fig.7 Streamline and pressure countour of sections

5 结 论

1) 窄条翼面积中心距离尾舵前缘根部5～6倍直径、在迎角等于33° 到40° 时，模型会进入极限环摇滚；去掉窄条翼或尾舵后，模型均不会进入极限环摇滚；而改变窄条翼的位置，也会使模型从不稳定转变为稳定。

2) 导致模型进入摇滚的直接原因是背风尾舵的动不稳定性；随着滚转角的增大，背风尾舵的动不稳定性减弱，整个模型又重新进入动稳定状态，最终导致模型进入极限环摇滚。

3) 从稳态和动态流场中都可以看出，摇滚与窄条翼片涡对尾舵的干扰密切相关，其中最显著的是片涡抑制了尾舵涡的产生和发展。

[1] NGUYEN L T, YIP L P, CHAMBERS J R. Self induced wing rock of slender delta wings: AIAA-1981-1883[R]. Reston: AIAA, 1981.

[2] DIMITRIADIS G, COOPER J E. Limit cycle oscillation control and suppression[J]. Aeronautical Journal, 1999, 103(1023): 257-263.

[3] NELSON H C, ANDREW S A. Experimental investigation of wing rock of slender wings and aircraft configurations, fluid dynamics of high angle of attack[M]. Berlin: Springer-verlag,1992: 413-422.

[4] ANANTHKRISHNAN N, SUDHAKAR K. Characterization of periodic motions in aircraft lateral dyanmics[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(3): 680-685.

[5] PLANEAUX J B, BECK J A, BAUMANN D D. Bifurcation analysis of a model fighter aircraft with control augmentation: AIAA-1990-2836[R]. Reston: AIAA, 1990.

[6] EVANS C. An investigation of large amplitude wing-rock[J]. The Aeronautical Journal, 1984, 38(873): 55-57.

[7] CHADERJIAN N M. Navier-Stokes prediction of large-amplitude delta-wing roll oscillations[J]. Journal of Aircraft, 1994, 31(6): 1333-1340.

[8] NELSON R C, ARENA A S, THOMPSON S A. Aerodynamic and flow field hysteresis of slender wing aircraft undergoing large-amplitude motions: AGARD CP-498 [R]. Neuilly: AGARD,1992.

[9] BRANDON J M, NGUYEN L T. Experimental study of effects of forebody geometry on high angle of attack static and dynamic stability: AIAA-1986-331[R]. Reston: AIAA, 1986.

[10] ROSS A J. Investigation of nonlinear motion experienced on a slender-wing research aircraft[J]. Journal of Aircraft, 1972, 9(9): 625-631.

[11] LIEBST B S. The dynamics, predicition, and control of wing rock in high-performance aircraft[J]. Philosophical Transactions of Royal Society, 1998, 356(1745): 2257-2276.

[12] ORLIKRUCKEMANN K J. Aerodynamic aspects of aircraft dynamics at high angles of attack[J].Journal of Aircraft, 1983, 20(9): 737-752.

[13] ERICSSON L E. Various sources of wing rock[J]. Journal of Aircraft, 1990, 27(6): 488-494.

[14] 姜浴标, 孙海生, 张钧, 等. 不同部件对机翼摇滚特性影响的风洞试验研究[J]. 飞行力学， 2002, 20(4): 39-43.

JIANG Y B, SUN H S, ZHANG J, et al. Investigation on wing rock in a low speed wind tunnel for fighter with different configurations[J]. Flight Dynamics, 2002, 20(4): 39-43 (in Chinese).

[15] 刘伟, 刘小亮, 张涵信, 等. 大攻角运动时的机翼摇滚问题综述[J]. 力学进展， 2008, 38(2): 214-228.

LIU W, LIU X L, ZHANG H X, et al. A review on investigations of wing rock problems under high angles of attack[J]. Advances in Mechanics, 2008, 38(2): 214-228 (in Chinese).

[16] ALLEN J M. Aerodynamics of an axisymmetric missile concept having cruciform strakes and in-line rail fins form Mach 0.60 to 4.63: NASA/TM-2005-213541[R]. Washington, D.C.: NASA, 2005.

[17] 阎超. 计算流体力学方法及应用[M]. 北京： 北京航空航天大学出版社， 2006: 18-23.

YAN C. CFD method and applications[M]. Beijing: Beihang University Press, 2006: 18-23 (in Chinese).

[18] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京： 北京理工大学出版社， 2008: 36-41.

QIAN X F, LIN R X, ZHAO Y N. Missile flight mechanics[M]. Beijing: Beijing Institute of Technology Press, 2008: 36-41 (in Chinese).

[19] DUBUC L, CANTARITI F, WOODGATE M, et al. Solution of the unsteady Euler equations using an implicit dual-time method[J]. AIAA Journal, 1998, 36(8): 1417-1424.

[20] ROE P. Approximate Riemann solvers, parameter vectors, and different schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.

[21] 达兴亚, 陶洋, 赵忠良. 基于预估校正和嵌套网格的虚拟飞行数值模拟[J]. 航空学报， 2012, 33(6): 977-983.

DA X Y, TAO Y, ZHAO Z L. Numerical simulation of virtual flight based on prediction-correction method and chimera grid[J]. Acta Aeronautica et Astronatica Sinica, 2012, 33(6): 977-983 (in Chinese).

Rockmotionandflowmechanismofmissileconfigurationwithstrakewings

FENGLiming*,DAXingya,WUJunqiang,ZHAOZhongliang

HighSpeedAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

Bluntforebodymissileconfigurationwithstrakewingshasexcellentlongitudinalaerodynamiccharacteristics,buthasseriousproblemsinlateralstabilitytoinduceuncommandedmotioninunsteadilylateraldirectionwhenthemissilemaneuversrapidly.Free-to-rollaerodynamicsandflowmechanismofmissilewithstrakewingsarestudiedthroughhighspeedwindturnelfree-to-rolltestsandnumericalsimulation.Resultsofsimulationsagreewellwithwindtunneltestresults.Studyshowsthatmodelentersintolimitcyclerockwhenthedistancebetweenthecenteroftheareaofstrakewingsandleadingedgeoftailfinsis5to6diameters.Positionofstrakewingshassignificanteffectonthestabilityofmodel.Themodelwillnotenterintolimit-cyclerockwhenstrakesortailfinsareremoved.Spacialflowcharacteristicsshowthatthewingvorticesgeneratedbystrakewingscanstronglyinterfereleewardfinstoaffecttheformationanddevelopmentoffinvortices.Thisleadstothelossofdynamicstabilityofleewardfins,andmodelthusenterslimit-cyclerock.

strakewing;missile;limit-cyclerock;dynamic;flowinterference

2016-05-09；Revised2016-08-02；Accepted2016-08-24；Publishedonline2016-09-260950

URL：www.cnki.net/kcms/detail/11.1929.V.20160926.0950.004.html

s：NationalNaturalScienceFoundationofChina(11372336,91216203,11532016)

2016-05-09；退修日期2016-08-02；录用日期2016-08-24； < class="emphasis_bold">网络出版时间

时间：2016-09-260950

www.cnki.net/kcms/detail/11.1929.V.20160926.0950.004.html

国家自然科学基金 (11372336,91216203,11532016)

＊

.E-mailfenglm8201@163.com

冯黎明， 达兴亚， 吴军强， 等． 窄条翼布局导弹摇滚特性及流动机理J． 航空学报,2017,38(4):120410.FENGLM,DAXY,WUJQ,etal.RockmotionandflowmechanismofmissileconfigurationwithstrakewingsJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):120410.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0252

V211.3

A

1000-6893(2017)04-120410-09

(责任编辑： 鲍亚平， 张晗)

＊Correspondingauthor.E-mailfenglm8201@163.com