仿人跑步机器人稳定性研究

赵子傧

(上海理工大学 机械工程学院，上海 200093)

仿人跑步机器人稳定性研究

赵子傧

(上海理工大学 机械工程学院，上海 200093)

针对仿人跑步机器人跑步过程中不易控制、容易跌倒的问题，将机器人跑步过程分为起跳、飞行两个阶段，分别采用ZMP与角动量定理进行稳定性分析。在起跳阶段，推导出机器人ZMP轨迹的计算公式，飞行阶段的角动量与起跳阶段的起跳瞬间角动量相同，因此根据起跳瞬间的角动量大小判断机器人在飞行阶段是否会发生翻转。仿真结果显示，机器人起跳阶段ZMP轨迹始终位于机器人的支撑多边形之内，飞行阶段的动量矩为0.01 kg·m2/s,说明机器人能够保持稳定。

跑步机器人；稳定性；ZMP；角动量

跑步机器人研究开始于上世纪80年代，最早的是Raibert 等人[1]，Raibert团队采用数种方法研制出跳跃机器人，这些方法为后来机器人的动态研究提供了早期的原则[2]。近年来跑步机器人研究受到越来越多的重视[3-5]，2003年以后相继有日、美、法、韩等国成功研制出数款跑步机器人，比如日本的Asimo，Athlete机器人。国内仿人跑步机器人研制还处于实验室研究阶段，目前还没有研制出仿人跑步机器人样机。清华大学陈恳、付成龙等人提出了跑步机器人截面稳定性判据[6]；哈尔滨工业大学洪炳熔等[7]研究了跑步机器人的基本运动模型以及控制方法；上海交通大学雷旭升[8]等以最小能量方程为优化了跑步机器人运动轨迹。

仿人跑步机器人脚掌和地面之间存在单边约束，这种双足系统本质上是不稳定的系统[9]，同时仿人机器人机械结构复杂，因此不易控制[10]、稳定性差。稳定性较差以及能耗较高的问题已成为仿人机器人实用化进程的两大障碍[11]，国内尚未研制出仿人跑步机器人样机，稳定性是其中很重要的原因。目前，步行机器人的稳定性研究较多[12-13]，而跑步机器人的稳定性还需要更加的深入研究。鉴于以上问题，本文对跑步机器人稳定性进行了研究，将跑步过程分为起跳与飞行阶段各自进行分析，得到了跑步机器人的稳定性判据，并对该方法进行了仿真验证。

1 机器人稳定性分析

1.1 起跳阶段稳定性

仿人跑步机器人在起跳阶段有一只脚着地，因此稳定性判据可以借鉴步行机器人稳定性判别方法：机器人ZMP必须始终位于机器人的支撑多边形以内[14]。

图1描述了机器人压力分布与ZMP的关系。如图1(a)所示，当地面对机器人足底作用力基本均匀分布时，机器人ZMP位于足底中间位置；如图1(b)，当地面作用力向机器人脚前端偏移时，机器人ZMP处于机器人脚的前部；极端情况下如图1(c)所示，当所有作用力均由机器人脚尖承受时，此时机器人ZMP便位于机器人脚尖位置，在这种情况下，由于机器人足底位置与地面不再保持接触，因此一个轻微的外界扰动作用于机器人身上都有可能使机器人旋转或者跌倒。为了提高仿人机器人运动的稳定性，ZMP必须位于机器人支撑多边形的内部，并距离支撑多边形边界有一定的距离。式(1)和式(2)为仿人机器人在起跳阶段的ZMP计算公式

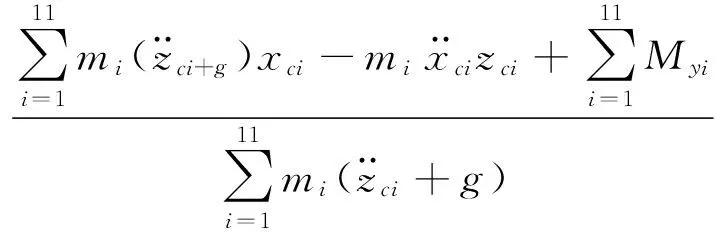
(1)

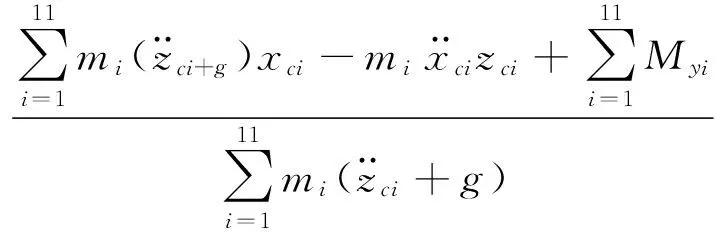
(2)

图1 机器人压力分布与ZMP关系

1.2 飞行阶段稳定性

机器人在飞行阶段处于腾空状态，与地面没有接触，只受重力与惯性力的作用，因此在此阶段机器人作自由落体运动。由达朗贝尔原理得

(3)

(4)

其中，ai为机器人杆件 的质心惯性加速度；1ci为机器人杆件i质心与重心的距离；Mi为机器人杆件 在飞行阶段所受的力矩；M为机器人杆件绕机器人质心的合力矩。将式(3)带入到式(4)得

(5)

对式(5)进行积分，得到机器人在飞行阶段的角动量为

(6)

其中ts，tf，T分别为机器人起跳阶段持续时间、飞行阶段持续时间以及单步长(右脚落地到下一次左脚落地之间的距离)持续时间，T=ts+tf，k为机器人步数，Li为机器人杆件i角动量。在飞行阶段，机器人所受外力矩为零，角动量守恒，即在飞行阶段机器人角动量保持不变，设为常数C，则由式(6)得

(7)

若C较大，则机器人在飞行过程中容易发生翻转，为此在机器人起跳末端必须控制C为零或者接近于零，即

(8)

其中，ε为常数，其取值与跑步机器人的跑步速度以及机器人质量等因素有关。

2 机器人落地时的碰撞分析

2.1 碰撞分析

机器人在飞行阶段结束落地，落地脚与地面碰撞，速度变为零。碰撞的产生必然会影响机器人的稳定性。为了分析机器人的碰撞问题，对机器人的碰撞作如下假设：(1)碰撞为瞬时完成，碰撞过程中脚与地面不发生打滑；(2)碰撞过程中只考虑碰撞力的作用，其他诸如摩擦力等忽略不计；(3)碰撞后机器人脚始终与地面接触(机器人脚底可能有弹簧等缓冲装置)。

在起跳阶段，机器人自由度为10，但在飞行阶段脱离地面约束，因此在矢状面内增加了两个转动与一个移动自由度，此时自由度变为13。设机器人独立广义为x=[θ,p,r]T，其中θ为机器人关节转角，θ=[θ1,θ2,…,θ12]；p,r分别为机器人质心在参考坐标系的位置与方向矢量。在机器人着地的瞬间，机器人自由度为10，机器人的拉格朗日方程为

(9)

(10)

即

(11)

将式(11)在碰撞时间Δt内进行积分

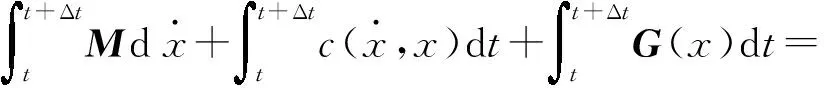
(12)

根据前文假设，碰撞是在瞬时完成的，因此Δt→0，在取此种极限的情况下，由式(12)得到

(13)

机器人落地后瞬间落地脚的速度降为零，因此

(14)

将式(12)带入式(11)得到

(15)

I#为6×6的单位矩阵。

因此，若要减小着地时脚与地面的碰撞，提高机器人的稳定性，需要从两方面考虑：(1)尽量减小落地前落地脚的速度，需在机器人的轨迹规划时予以考虑；(2)使机器人在落地时与地面有一个缓冲，跑步机器人质心与参考坐标系原点位置的连线可以看作一条“弹簧腿”，此“弹簧腿”在落地时一边伸缩运动一边旋转运动，通过调整落地时“弹簧腿”的伸缩与旋转可以达到缓冲目的，或在落地脚底面加上弹簧等的缓冲装置以达到缓冲目的。本文采用第一种方法，对机器人轨迹规划时将机器人落地速度规划为零。

2.2 机器人脚的轨迹规划

假设机器人跑步时第一次落地为右脚落地，则到下一次右脚落地时机器人完成一个跑步周期，经历了右脚起跳、飞行、左脚落地起跳、飞行、右脚落地5个阶段。以右脚为例采用三次样条曲线拟合脚的轨迹，以右脚落地时开始计时。右脚运动的边界条件为

(16)

(17)

Ds为单步长，在t=T0时，右脚底面中心在参考坐标系中达到最高点(Da，Ha)，xf，zf为右脚底面中心在参考坐标系在x，z方向的坐标。另外，由于在t=0时刻机器人右脚刚离开地面，此时初速度为0；而t=(k+2)T时刻，机器人右脚从空中落地，若此时右脚在x轴和z轴上的速度分量为vxt和vzt，得到右脚运动速度的边界条件(第二类边界条件)[15]

(18)

(19)

为减小落地时脚与地面的碰撞，将vxy和xzt规划为0。令Ts=0.204 s，单步长Ds=0.47 m，飞行时间Tr=0.067 s，(Da，Ha)为(0.137 m，0.17 m)则根据式(16)～式(19)拟合出右脚的轨迹如图2和图3所示。

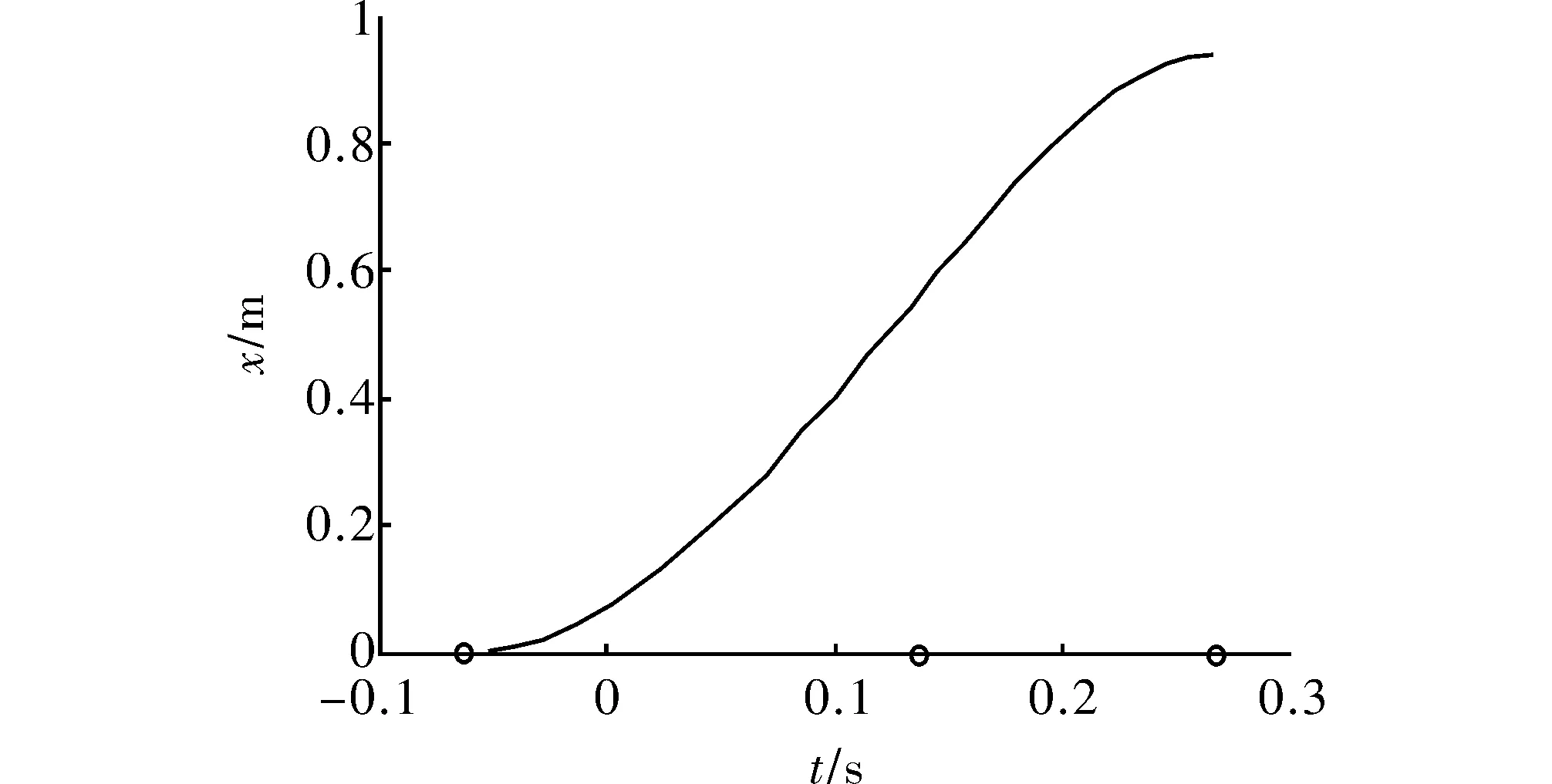
图2 机器人右脚在x轴的轨迹

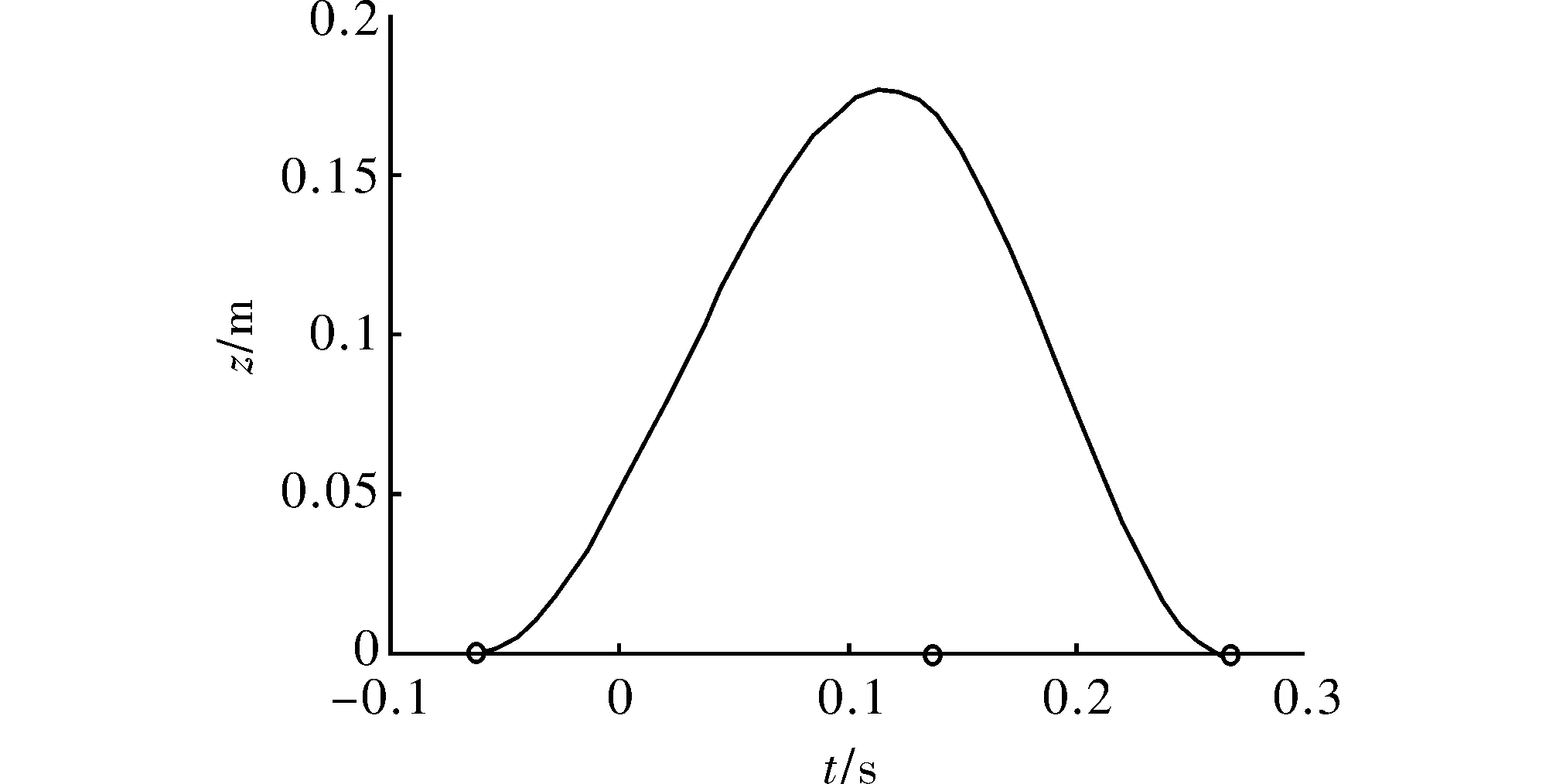
图3 机器人右脚在z轴轨迹

3 仿真分析

为检验方法的正确性与有效性，对该方法进行仿真验证，所采用的机器人主要参数如表1所示。首先规划了机器人的质心轨迹与双脚轨迹，然后建立了机器人坐标系，对机器人正逆解进行分析，得到了机器人的关节转角，并对机器人进行动力学分析，求得机器人动力学逆解；最后将机器人关节转角带入Matlab中进行仿真验证。

根据式(1)和式(2)计算机器人在起跳阶段的ZMP轨迹，如图4所示，可以看出在起跳阶段机器人的ZMP轨迹始终位于机器人的支撑多边形以内，说明机器人在起跳阶段是稳定的；计算机器人在起跳结束时刻的动量矩，在起跳结束时刻机器人的动量矩为0.01 kgm2/s，接近于0，说明机器人在飞行阶段不会发生翻转。图3给出了机器人的Matlab仿真杆状图，由图3可以看出机器人实现了稳定的跑步动作，单步长为0.47 m。

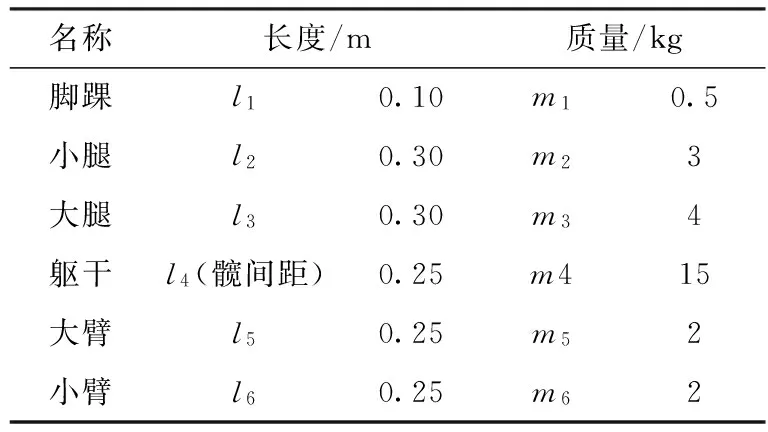
表1 机器人主要参数

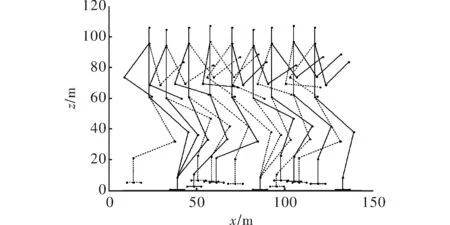
图4 跑步机器人杆状图

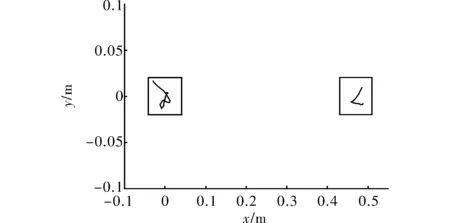
图5 机器人起跳阶段ZMP轨迹

4 结束语

针对跑步机器人容易跌倒的问题进行了分析，为维持稳定，在起跳阶段机器人ZMP必须位于机器人的支撑多边形以内，在飞行阶段机器人的角动量必须为零或接近于零。此外为减小机器人落地时脚与地面产生碰撞对稳定性的影响，须控制落地速度或增加缓冲。仿人跑步机器人的进步需要基础理论与机器人样机的共同推进，将机器人理论应用于仿人跑步机器人、提高仿人跑步机器人运动能力，是目前仿人跑步机器人工作的重点与难点。

[1] Park J,Kim Y K,Yoon B,et al.Design of biped robot inspired by cats for fast running[J].EIectronics Letters,2014,50(10):730-731.

[2] Raibert M,Tello E R.Legged robots that balance[J].IEEE Expert,1986,1(4):89-89.

[3] Sullivan T,Seipel J.3D dynamics of bipedal runn- ing:effects of step width on an amputee- amputee-inspired robot[C].HA,USA: IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014),IEEE,2014.

[4] Amagata Y,Nakaura S,Sampei M.The running of humanoid robot on uneven terrain utilizing output zeroing[C].Qubic:SICE Annual Conference,IEEE,2008.

[5] Cho B K,Kim J H,Oh J H.Online balance controllers for a hopping and running humanoid robot[J].Advanced Robotics,2011,25(9-10):1209-1225.

[6] 贾丁.仿人机器人概述[J].机器人技术与应用,2002(5):6-7.

[7] 洪炳熔,贺怀清.虚拟人的步行和跑步运动控制方法的研究[J].高技术通讯,2001,11(3):91-95.

[8] Lei X S,Su J B.Running trajectory generation for humanoid robot[C].HongKong:Proceedings of 2004 International Conference on Machine Learning and Cybernetics,2004.

[9] 彭胜军,税海涛,马宏绪.仿人跑步机器人稳定性与控制策略研究进展[J].控制工程,2011,18(1):142-146.

[10] 顾岩秀,华云松.双足载人机器人的结构设计及高度优化[J].电子科技,2016,29(2):77-80.

[11] 杨亮,傅瑜,付根平,等.基于能效优化的仿人机器人跑步步态优化与控制[J].计算机科学,2016,43(6):59-63.

[12] 王险峰,李建平,王辉.基于ZMP的仿人机器人跑步运动模式[J].计算机研究与发展,2013,50(10):2206-2211.

[13] Jungyup Kim,Youngseog Kim. Human-like gait generation for biped android robot using motion capture and ZMP measurement system[J].International Journal of Humanoid Robotics,2010,7(4):511-534.

[14] 梶田秀司,管贻生.仿人机器人[M].北京:清华大学出版社,2007.

[15] 张明,文世鹏.应用数值分析[M].北京:石油工业出版社,2001.

Research on Stability of Humanoid Running Robot

ZHAO Zibin

(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

Aiming at the problem of humanoid running robot in the running process is not easy to control,easy to fall,the robot running process is divided into two stages: take-off phase and flight phase,the stability analysis is carried out by using ZMP and angular momentum theorem respectively. In the take-off phase,the calculation formula of the ZMP trajectory of the robot is derived; The angular momentum of the moment of Take-off is same with the angular momentum of the flight phases,therefore,according to the angular momentum of the moment of take-off to judge whether the robot will turn over the flight phase. The simulation results show that the ZMP trajectory of the robot is always in the support polygon of the robot,and the moment of momentum of the flight phase is 0.01kg·m2/s,which indicates that the robot can keep stable.

running robot;stability;ZMP;angular momentum;simulation.

TP242

A

1007-7820(2017)11-089-04

2016- 10- 22

赵子傧(1990-),男，硕士研究生。研究方向：机器人学。

10.16180/j.cnki.issn1007-7820.2017.11.024