基于FPFH特征和模糊聚类的自适应点云压缩

王艺楠，郝矿荣,2，杨焕宇,3

(1.东华大学 信息科学与技术学院，上海 201620；2.数字化纺织服装技术教育部工程研究中心，上海 201620；3.上海开放大学，上海 200233)

基于FPFH特征和模糊聚类的自适应点云压缩

王艺楠1，郝矿荣1,2，杨焕宇1,3

(1.东华大学 信息科学与技术学院，上海 201620；2.数字化纺织服装技术教育部工程研究中心，上海 201620；3.上海开放大学，上海 200233)

针对三维激光扫描技术获取的点云数据存在大量冗余问题，文中提出了一种基于快速点特征直方图和模糊C均值聚类(FPFH-FCM)的点云压缩算法。利用FPFH特征在点云模型不同几何位置的分布差异，基于FCM算法自适应地将点云集合分为特征点集和非特征点集。并建立压缩准则：对非特征点集进行较大比例的压缩，去除冗余点；对特征点集进行较小比例的压缩，尽量保留更多的特征点，以实现点云压缩。在对比试验中，分别使用提出的基于FPFH特征的点云压缩算法与基于曲率特征的点云压缩算法，对人体点云数据进行压缩，对比压缩后点云的曲面重建效果，同时使用原始点云与压缩后点云之间的Hausdorff距离作为压缩误差评价指标，结果证明，该压缩算法能够更好地保留重建模型的细节特征，具有更高的压缩精度。

点云压缩；快速点特征直方图；模糊C均值聚类；泊松曲面重建；Hausdorff距离

三维激光扫描技术以其非接触、高精度等特点广泛应用于空间信息获取，但扫描得到的海量点云数据通常在几十万，甚至上百万的数量级，且存在大量冗余，这就增加了点云数据存储、传输、运算负担和后续处理工作的难度[1]。

点云数据在虚拟现实、逆向工程、模式识别和机器视觉领域广泛应用。例如即时定位与地图构建技术(SLAM)是目前实现真正全自主移动机器人的关键，这项技术在实际应用中需要对获取的点云数据进行去噪、压缩等预处理。近年的热门技术-虚拟现实也需要在三维重建前对点云数据进行去噪、压缩、网格化等处理。因此，对三维点云数据的压缩研究是当前的一个研究热点。

不同应用场景中，对压缩后点云数据的要求也有很大差别。例如用于SLAM的点云数据[2]，压缩后只需保留可完成点云拼接[1]的几何特征点，使得经过点云拼接、信息融合后重构出的点集能够刻画出实际场景的轮廓，无需保留大量表面细节信息。而在虚拟现实[3]应用中的点云数据则需要保留更多的细节特征，使其通过三维重建获得逼近真实的场景模型，带来更好的虚拟现实体验。

点云压缩不仅要有较高的压缩比，还需要保留足够多的特征点。因而点云压缩问题可定义为：k时刻从视点Vk获取的点云集合为Mk，求取Mk的一个子集Pk，在满足预设压缩比ρ的情况下

(1)

使压缩后的子集Pk保留足够多的特征点，即

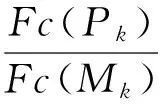
(2)

其中， 为特征点数量度量函数； 为设定的特征点保留率。

现有的压缩算法可以分为两类：(1)基于距离的压缩算法。如包围盒法[4]、均匀/非均匀网格法[5]、自适应距离法[6]等。这类方法简单、高效，对均匀的点云能够取得一定效果，但只适应于表面不复杂、曲率变化不大的物体的数据压缩；(2)基于特征[7]的压缩算法。如曲率采样法[8]、曲线拟合法[9]等。这类方法虽然计算快速、容易，但是无法获得太多信息，因为这类方法只使用很少的几个参数值来近似的表示一个点的k邻域的几何特征，仅能表征某些相同或者相近的特征值，无法获得太多信息，而对于包含大量特征信息的复杂模型，无法保留其全局特征信息。

作者引入一种新的复合特征—点特征直方图(Point Feature Histogram，PFH)[10]，该特征经过多年的发展和实践，被证明是一种非常有效的点云描述特征，并广泛应用于点云处理[11]。由于快速点特征直方图(Fast Point Feature Histogram，FPFH)[12]在仍保留PFH大部分识别特性的基础上将PFH的理论计算复杂度从O(n·k2)降至O(n·k)，因而作者选用FPFH特征。利用点云的FPFH特征在模型不同几何位置的显著分布差别，有选择的剔除冗余点，尽可能多的保留特征点，使得压缩后的点云模型在一定压缩率下，可以保留更多用于曲面重建、物体识别的几何特征，获得更好的压缩效果，同时保证算法的计算速度在可接受范围内。

1 计算快速点特征直方图

1.1 PFH特征描述子

点特征直方图(PFH)[10]的计算方式是通过参数化查询点与邻域点之间的空间差异，形成一个多维直方图对点的 邻域几何属性进行描述。具有3个优势：(1)刚体变换不变性；(2)采样一致性，改变采样密度，特征保持不变；(3)轻微噪声不变性。具有这些不同优势的特征描述子往往能在实际应用中带来更好的效果[13-14]。

图1所示为查询点Pq及其PFH计算的影响区域，Pq位于半径为 的圆球中心位置，Pq的所有k邻元素(即与点Pq的距离小于半径r的所有点)全部互相连接在一个网络中。PFH描述子通过计算k邻域内所有两点之间的法线偏差而得到直方图。如图2所示，为了计算k邻域内任意两点Ps和Pt对应的法线ns和nt之间的相对偏差，在Ps点上定义一个固定的三维直角坐标系uvw，并将这一uvw坐标系平移至Pt点处。

图1 查询点 及其 邻域

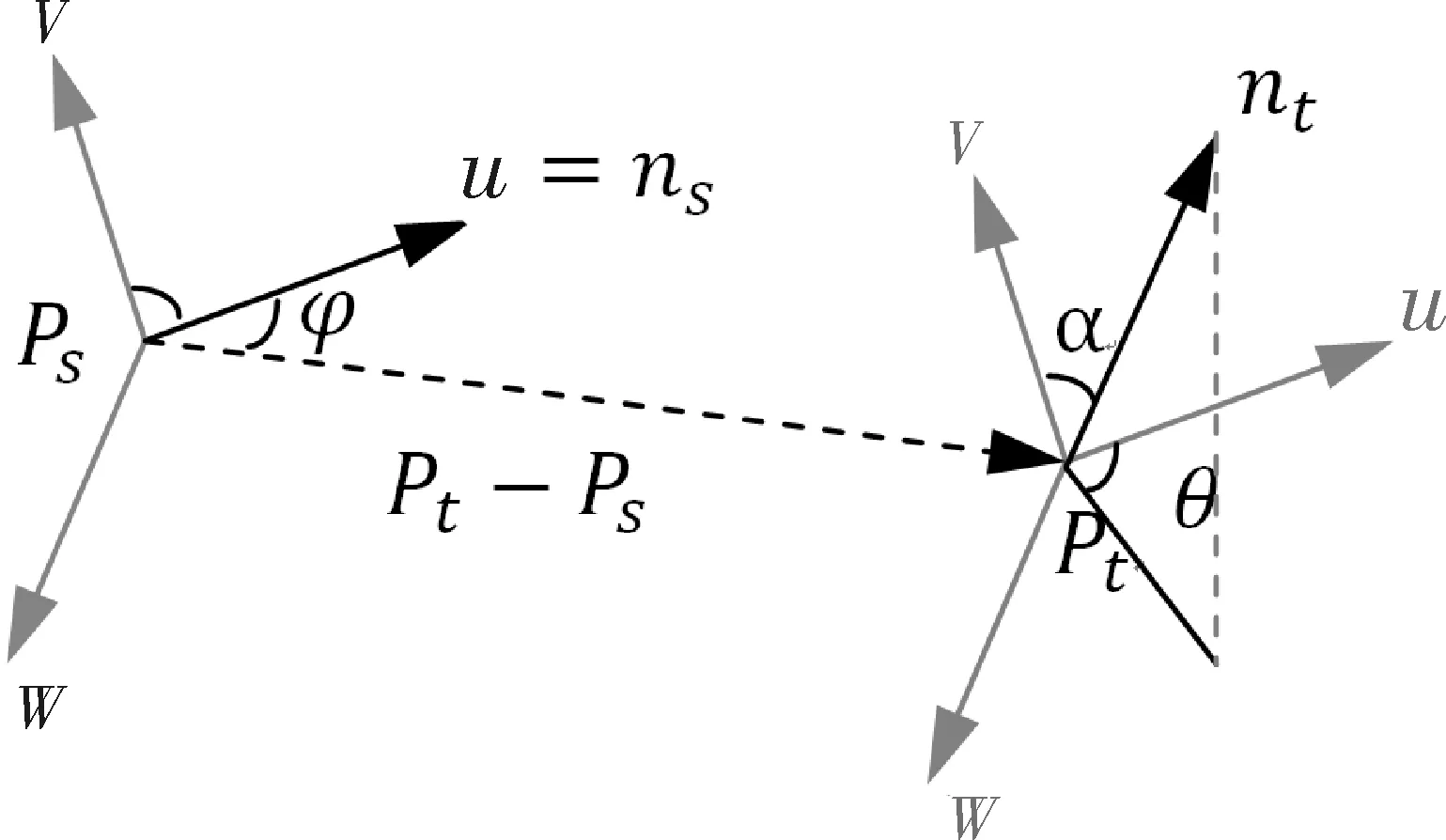
图2 定义一个固定的局部坐标系

使用图2中定义的uvw坐标系，法线ns和nt之间的偏差可以通过式(3)和式(4)的计算后使用4组值(α,φ,θ,d)来表示

(3)

(4)

式(4)中，d是Ps和Pt两点之间的欧氏距离，d=‖Ps-Pt‖。

按照上述计算方式，Pd的k邻域内任意两点的法线偏差都可以用4组值(α,φ,θ,d)来表示。将邻域内所有的4组值以某种统计的方式放进直方图中，就得到了Pq点的特征直方图。

PFH的理论计算复杂度是O(n·k2)，n是点的数量，k是最近邻的个数。对于实时应用或接近实时的应用，密集点云的PFH计算存在性能瓶颈。因而提出了PFH的简化版-快速点特征直方图(FPFH)[12]，其计算复杂度减少至O(n·k)，并保持了较好的和PFH接近的特征区分能力。

1.2 FPFH特征描述子

快速点特征直方图(FPFH)[12]是由PFH改进而来，其计算原理如图3所示。

图3 FPFH计算原理

FPFH的计算过程如下：

(1)对于每一个查询点(Pq)，计算该点和灰色区域内邻域点之间的元组(α,φ,θ)，第一步结果称为简化的点特征直方图(Simplified Point Feature Histograms，SPFH)；

(2)确定查询点(Pq)的每个邻域点的k邻域，分别计算每个邻域点的SPFH；

(3)使用Pq点的SPFH值和它邻域点Pk的SPFH值按式(5)计算获得 FPFH。

式(5)中，以Pq和其邻近点Pk之间的距离作为权重wk。FPFH利用三元组(α,φ,θ)描述查询点与邻域点之间法向量的偏差，将三元组中每个分量的统计值归一化为[0,100]，并划分11个区间，这样共形成33个角度区间用于元组值的数量统计，由此获得一个33维的特征向量。

1.3 FPFH特征分析

图4和图5分别是实际平面上的点和角点的FPFH直方图。在平坦的表面上，由于查询点与周围点的法线方向差异比较小，描述法线差异的各个角度分量都集中在特定的区间，因而FPFH统计直方图的分布比较集中。

图4 实际平面点的FPFH图

而位于边缘、角点处，由于查询点与周围点的法线方向差异较大，描述法线差异的各个角度分量会在整个区间上出现，因而FPFH统计直方图的分布比较均匀。

图5 实际角点的FPFH图

2 模糊C均值(FCM)聚类算法

模糊C均值(FCM)聚类算法[15]在众多模糊聚类算法中应用最广泛且较成功，它通过优化目标函数得到每个样本点对所有类中心的隶属度，从而确定样本点的类属，以实现样本的自动分类。对给定的样本集X={x1,x2,…,xn}⊆Rd，在FCM算法中，设U=(uij)n·c为隶属度矩阵，V=[v1,v2,…,vc]为c个类中心点组成的矩阵，式(6)定义了类内平均误差函数J(X,U,V)

(6)

其中，m∈[1,+∞)是模糊指数；c是样本集聚类的类别；uij(1≤i≤n,1≤j≤c)表示xi在第j个类的隶属度值，并满足以下3个约束条件

(7)

1≥uij≥0,1≤i≤n,1≤j≤c

(8)

(9)

此外，vj表示第j类的类中心；d2(xi,vj)表示样本xi和类中心vj的相似度量，一般用欧式距离表示。

FCM的实现包含下列步骤：

(1)选定聚类数目c、模糊指数m、最大迭代次数T和阈值ε，并令迭代计数器t=0，初始化隶属度矩阵；

(2)利用拉格朗日乘法计算聚类中心V和隶属度矩阵U；

(3)根据当前V和U，计算目标函数式(6)中类内平均误差函数J(X,U,V)的值，若迭代次数>T或者相邻两次目标函数值的绝对值小于阈值ε，则算法停止；否则，令t=t+1转步骤(2)。

3 基于FPFH-FCM的点云压缩算法

3.1 问题描述

作者提出的压缩算法的基本思路是，利用点云的FPFH特征在不同几何位置的显著分布差别，选择性地剔除一些点。剔除的基本原则是：位于平坦表面的点应尽可能剔除，因为这种类型的点数量庞大，包含的几何特征较少；而位于几何体边缘、角点位置的点应尽可能保留，因为这些点能够定义几何体的形状，具有较大的几何区分度，点云的后续处理(如点云拼接)经常需要利用这些特征关键点做进一步处理。

为了能够自适应地将点云数据按照上述准则进行压缩，需要一种智能算法实现点云的自动分类。选取FCM( Fuzzy C-Means)[15]对点云数据进行聚类，将每个点云数据的FPFH(33维特征直方图)转化为数值向量作为训练样本，参数聚类数目C和加权指数m均设为2，使用这种无监督的机器学习算法可将点云数据自动聚类为特征点集和非特征点集。

3.2 算法流程

作者提出了一种基于FPFH和FCM的点云压缩算法，具体的算法流程如下

(1)在 时刻.通过扫描仪获取点云集合Mk={pi|i=1,…,m}，并构建集合Mk的索引树。其中m为集合包含的扫描点数量；

(2)计算Mk集合中每个点Pi的法向量ni，得到法向量集合Nk={ni|i=1,…,m}，并构建集合Nk的索引树；

(3)根据式(1)和式(2)计算集合中每个点的特征直方图hi，得到直方H={hi|i=1,…,m}；

(4)基于模糊C均值聚类算法对FPFH特征进行无监督聚类，获得特征点集和非特征点集；

(5)通过设置参数K(两类点集压缩率的比=非特征点集压缩比例：特征点集压缩比例)，给予非特征点集较高的压缩率，特征点集较低的压缩率(默认情况下：K=1.5:1)；

(6)合并压缩后的两类点集，获取压缩点云模型。

4 实例应用与分析

为验证算法的有效性，采用C++语言在Microsoft Visual Studio 2010上实现点云压缩算法，同时调用OpenGL库函数显示点云。作者使用包含复杂曲面的人体点云模型进行压缩实验，从不同压缩率下的压缩结果、压缩后模型的曲面重建效果、压缩误差3个方面对FPFH-FCM算法进行评价与分析，并与文献[16]中的算法进行对比。

4.1 不同压缩率下的压缩结果

作者提出的点云压缩算法中有两个参数需要设置，分别是K和ratio，其中K默认取值为1.5；ratio是整体点云的压缩比(剔除点数/输入点数)，可根据用户需求设定，这里分别选取ratio为0.7、0.8、0.9进行实验。

图6 不同压缩率下的压缩结果

图6为人体点云模型在不同压缩率下的压缩结果。其中图6(a)为人体模型的原始点云，共包含52 565个点；图6(b)为压缩至70%的点云模型，共包含15 770个点，其中保留11 174个特征点，4 596个非特征点；图6(c)为压缩至80%的点云模型，共包含10 513个点，其中保留7 453个特征点，3 060个非特征点；图6(d)为压缩至90%的点云模型，共包含5 257个点，其中保留3 727个特征点，1 530个非特征点。

从图6的点云压缩结果可以看出，FPFH-FCM算法自适应地在高曲率区域保留较多点，在平坦区域保留少数点，使得在不同压缩率下都具有较好的压缩效果，压缩后的点云模型特征信息保留较为完好，轮廓信息依然清晰可见。同时该算法可根据实际情况对参数K(两类点集的压缩比)进行调整，改变特征点的保留比例，大幅提高算法的灵活度。

4.2 压缩算法对比

为验证压缩算法的有效性，将FPFH-FCM点云压缩算法与基于曲率特征的点云压缩算法[16]对比，分别使用两种算法在同一实验数据、相同压缩率下进行实验，并从曲面重建效果和压缩误差两个方面对比两种算法的压缩效果。

4.2.1 曲面重建效果对比

为了更加形象地描述点云模型的压缩效果，常常需要进行点云曲面重建。选取Poisson曲面重建算法，具体实现过程如下：(1)输入有向点云数据；(2)建立八叉树空间；(3)计算向量场；(4)解泊松方程求指示函数；(5)提取等值面。

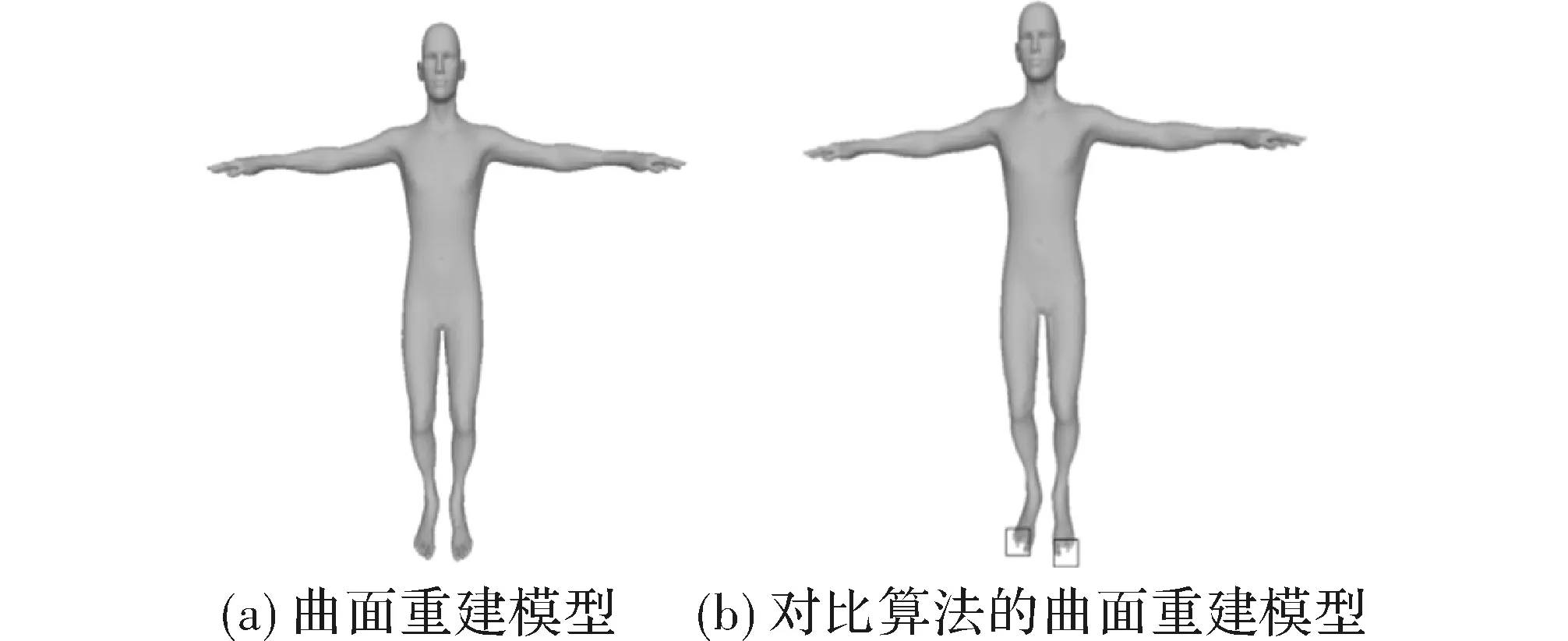
图7 基于曲率特征进行70%的点云压缩

图8 两种算法压缩后曲面重建模型的细节对比

使用基于FPFH和FCM的点云压缩算法将点云压缩至15 272个点(ratio=70%)，压缩后的曲面重建模型如图7(a)所示；使用基于曲率特征的点云压缩算法进行同样比例的压缩，压缩后的曲面重建模型如图7(b)所示；两种算法压缩后曲面重建模型的细节对比如图8(a)和图8(b)所示，文中所提算法的重建模型可以完好地保留模型细节特征，而对比算法的重建模型有部分细节缺失。综上所述，FPFH-FCM算法压缩后的点云模型可在高曲率区域保留更多的特征信息，压缩后的曲面重建模型可以更好的展现人体细节部位。

4.2.2 压缩精度对比

为评估点云压缩算法的质量，需要衡量压缩后点云与原始点云之间的压缩精度。作者使用压缩后点云与原始点云之间的Hausdorff距离作为压缩精度的评价指标。Hausdorff距离是描述两组点集之间相似程度的一种量度，给定两个有限集合A=a1,a2,…,an和B=b1,b2,…,bn，则这两个点集合之间的Hausdorff距离定义为

H(A,B)=max(h(A,B),h(B,A))

(10)

在相同压缩率下，分别比较两种算法[17]获得的压缩后点云集合与原始点云集合之间的Hausdorff距离，结果如表1所示。

表1 Hausdorff距离对比

如表1所示，在不同压缩率下，基于FPFH-FCM压缩算法计算获得的Hausdorff距离均小于对比算法计算获得的Hausdorff距离，表明FPFH-FCM算法具有更好的压缩精度。

5 结束语

作者提出一种基于FPFH-FCM的点云压缩算法，利用点云FPFH特征在模型不同几何位置的显著分布差异，基于模糊C均值聚类算法自适应地将点云数据分为特征点集和非特征点集，然后建立压缩准则：对非特征点集进行较大比例的压缩，去除冗余点；对特征点集进行较小比例的压缩，尽量保留更多的特征点，以实现点云压缩。同时，该算法可通过调整参数压缩率ratio，自动实现不同点云压缩率的要求。

在实验仿真部分，分别从不同压缩率下的压缩结果、压缩后模型的曲面重建效果、压缩误差3个方面对FPFH-FCM算法进行评价与分析，并与文献[17]中的算法进行对比。实验结果证明提出的FPFH-FCM压缩算法能够更好的保留重建模型的细节特征，具有更高的压缩精度。

[1] 王英男,戴曙光.基于单位四元数法的激光点云拼接算法研究[J].电子科技,2015,28(6):202-204.

[2] 李玉.基于3D激光点云的无人车城市环境SLAM问题研究[D].北京:北京理工大学,2016.

[3] 刘军,耿国华.文化遗址的三维真实感建模与虚拟展示技术[J].计算机工程,2010,36(20):286-290.

[4] 刘涛,徐铮,沙成梅,等.基于包围盒法的散乱点云数据的曲率压缩[J].科学技术与工程,2009,9(12):3333-3336.

[5] 姚顽强,郑俊良,陈鹏,等.八叉树索引的三维点云数据压缩算法[J].测绘科学,2016,41(7):18-22.

[6] 吴禄慎,俞涛,陈华伟.基于自适应椭圆距离的点云分区精简算法[J].计算机应用与软件,2016,11(2):42-45.

[7] 史宝全,梁晋,张晓强,等.特征保持的点云精简技术研究[J].西安交通大学学报,2010,44(11):37-40.

[8] 代星,崔汉国,胡怀宇.基于曲率特征的点云快速简化算法[J].计算机应用,2009,12(11):3030-3032.

[9] 韩江,江本赤,夏链,等.基于轮廓关键点的B样条曲线拟合算法[J].应用数学和力学,2015,36(4):423-431.

[10] Rusu R B,Blodow N,Marton Z C,et al. Aligning point cloud data views using persistent feature histograms[C].CA,USA:IEEE/RSJ International Conference on Intelligent Robots and Systems,2008.

[11] 陆军,彭仲涛.基于快速点特征直方图的特征点云迭代插值配准算法[J].国防科技大学学报,2014,23(6):12-17.

[12] Rusu R B,Blodow N,Beetz M.Fast point feature histograms (FPFH) for 3D registration[C].PF,USA:IEEE International Conference on Robotics and Automation,IEEE Press,2009.

[13] Liu H,Hao K R,Ding Y S.New anti-blur and illumination-robust combined invariant for stereo vision in human belly reconstruction[J].Imaging Science Journal,2014,62(5):251-264.

[14] 刘欢,郝矿荣,丁永生,等.光照鲁棒的抗模糊新组合不变矩图像匹配方法[J].传感技术学报,2013,26(9):1258-1264.

[15] Pal N R,Pal K,Keller J M,et al.A possibilistic fuzzy C-means clustering algorithm[J].IEEE Transactions on Fuzzy Systems,2005,13(4):517-530.

[16] Song H,Feng H Y.A global clustering approach to point cloud simplification with a specified data reduction ratio[J].Computer-Aided Design,2008,40(3):281-292.

A Self-adaptive Simplification Algorithm for Point Cloud based on Fast Point Feature Histogram and Fuzzy Clustering

WANG Yinan1，HAO Kuangrong1,2，YANG Huanyu1,3

(1. School of Information Sciences and Technology,Donghua University,Shanghai 201602,China;2. Engineering Research Center of Digitized Textile &Fashion Technology,Ministry of Education,Shanghai 201620,China; 3.Shanghai Open University,Shanghai 200233,China)

Due to data redundancy in point cloud obtained by 3D scanning technology,this paper proposes a simplification algorithm for point cloud based on Fast Point Feature Histogram and Fuzzy C-Means(FPFH-FCM).Using the different distribution of FPFH in different geometric location of model,point cloud data is divided adaptively into feature point set and unfeature point set based on the FCM clustering algorithm. Then the two types of point set are compressed in different proportions,in order that the compressed point cloud can retain enough geometrical characteristics. For comparison experiments,we compress body point cloud model by our algorithm based on FPFH feature and comparing algorithm based on curvature feature respectively,then compare the effect of surface reconstruction of compressed point cloud，meanwhile，we evaluate the compression precision by Hausdorff distance of original point cloud and compressed point cloud,It is proved that our compression algorithm can preserve the details of the reconstruction model and get higher compression precision.

point cloud simplification;fast point feature histogram;fuzzy C-means algorithm;possion surface reconstruction; Hausdorff distance

TN911.73;TP391.41

A

1007-7820(2017)11-073-06

2016- 12- 24

国家自然科学基金(60775052)

王艺楠(1992)，女，硕士研究生。研究方向：计算机图形学。郝矿荣(1964)，女，博士，教授，博士生导师。研究方向：图像处理等。杨焕宇(1985-)，女，博士，讲师。研究方向：三维点云数据处理。

10.16180/j.cnki.issn1007-7820.2017.11.020