全面二孩政策下人口结构对经济发展影响研究

韩林峄，吴 晟，周海河，刘英莉，崔庆发

（昆明理工大学 信息工程与自动化学院，云南 昆明 650500）

全面二孩政策下人口结构对经济发展影响研究

韩林峄，吴 晟，周海河，刘英莉，崔庆发

（昆明理工大学 信息工程与自动化学院，云南 昆明 650500）

自2016年起，我国正式实施全面二孩政策。为了评估在二孩政策下人口结构对经济发展的影响。本文首先基于Leslie模型和灰色GM(1,1)模型，进行人口数量及结构预测。其次对人口结构和人均GDP进行单位根检验以及协整检验，再进行因果分析。最后将2017-2030年实施全面二孩政策下的人口结构与不实施全面二孩政策下的人口结构对比，并使用因果分析进行综合评价。实验结果表明，劳动力人口与城镇人口比重对经济发展影响可信度分别为 0.68和 0.60，结果可信度较高。实施二孩政策之后劳动力人口与城镇人口比重均大于实施二孩政策之前的比重。得出结论：在二孩政策的影响下，2017-2030年，我国经济会有所提升。

全面二孩；Leslie模型；GM(1,1)模型；因果关系检验

0 引言

中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。2015年十八届五中全会明确提出“全面实施一对夫妇可生育两个孩子”的政策，2015年 12月人大常委会表决通过了《人口与计划生育法》修正案，全面二孩政策于2016年1月1日起正式实施，目前正处于全面二孩阶段。

从当初实行计划生育政策调整到逐步放开生育政策再到全面实行二孩政策，我国的人口发展出现了一些新的特点[1]。2016年是我国自2000年以来出生人口最多的一年。国家卫计委表示，根据国家统计局公布的数字，我国2016年出生人口达1786万人，同比增长7.9%，二孩及以上占出生人口比重超过45%。就当前而言，“80后”是主要的婚育主体，因此对于未来新生人口的增减趋势，“80后”的生育意愿在其中起着很重要的作用。

生育政策是一个国家或地区重要的社会政策之一，它决定着这个国家或地区在今后相当一段时间内的人口发展态势（包括人口的规模、结构及质量等方面），对经济社会的发展起着至关重要的作用[2]。本文重点研究了在实施二孩政策后，人口结构对我国经济发展的影响。

1 基本理论

1.1 Leslie模型

Leslie模型是一种离散矩阵模型，它主要以年龄和性别为基础[3]。此模型的构建原理是：首先从年龄的角度对数据进行分组，以女性的分年龄别人口数作为分组标准，根据这些分组构造列向量。然后把列向量按照年龄别生育率、年龄别死亡率等标准重新排列组合，构建Leslie矩阵。最后再把分年龄别人口数的列向量与Leslie矩阵相乘，会得到一个新的列向量，它就是将来的女性人口数量，进而算出整体的男女比例。从而通过这种方法去推断人口总数。

Leslie是一个可以预测特定区域人口数量和各年龄阶段人数的预测模型。用这个模型进行预测的优势就是预测结果较为准确，因为它的数据核心就是人口相关自变量、性别分组及某一初始时期的人口发展，这些数据相对于其他同类型的数据而言具有一定的稳定性[4]。

设需要预测的起始时间为t年，用 ()xt表示人口数量，年龄组内女性生育率为ib，w为女性人口比例，存活率为 ()st，就第1年龄组的女性人口而言，第 1t+年的人口数可表达为（1）式：

同理，在第t年第i年龄组人数可表达为（2）式：

这个人数也是第 1t+年第 1i+年龄组的女性人口的人数。

构造Leslie矩阵如下：

1.2 协整和Granger因果检验

（1）序列平稳性检验

协整理论用于非平稳时间序列中[5]，主要是为了获得相应的均衡关系。要进行协整和因果分析，首要的就是对变量进行平稳检验，一般都采用ADF单位根方法来进行相关的检验操作，检验模型有以下三种。

模型1：没有时间趋势及常数项，检验公式为：

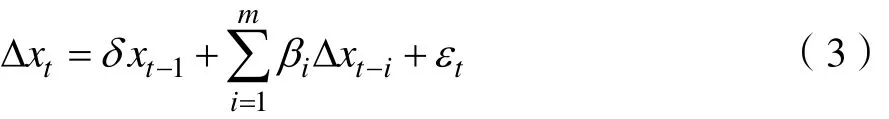
模型 2：包含常数项但不存在趋势项。检验公式为：

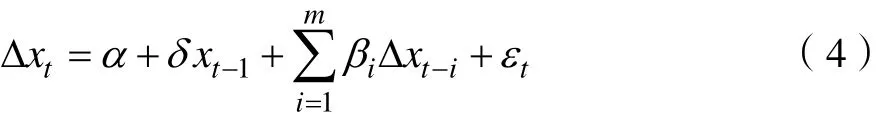
模型3：有时间趋势及常数项，检验公式为：

（2）协整、误差修正模型

协整理论中，若变量之间属于同一个阶数的单整序列，就可以构建协整方程对变量关系进行分析。若序列tx和ty都是单整序列，并且两个序列都不平稳，则对于OLS协整方程而言：

再对xt和yt进行协整检验，来判断残差εt的平稳性。若 xt和 yt不存在协整关系，则他们的任意组合都是非平稳的，从而证明残差εt也是不平稳的。若检验结果显示εt的平稳性很好，则可判断出xt和yt协整关系是良好的。

（3）Granger因果关系检验

某变量对另一变量而言是否存在因果变化，主要采用Granger因果关系检验法[6]来进行判断，通过以下两个变量回归模型来进行相关检验。

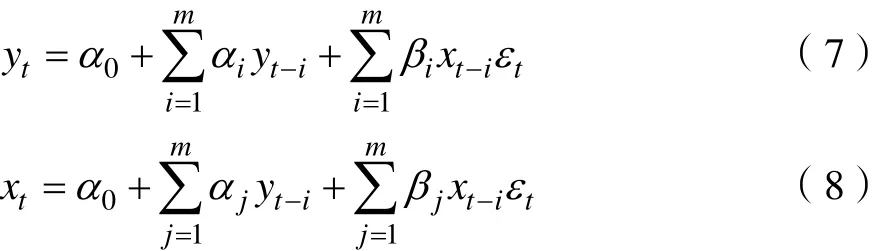
式中，若 βi=0（i=1,2,...m），则x不是造成y变化的原因；若拒绝 βi=0，则x是造成y变化的原因，得到的最终结论为：x相对于y具有Granger因果关系。同时，可以对 βi=0进行验证来判断y和x是否存在因果关系。

2 实验分析

2.1 人口结构预测

2.1.1 不实施全面二孩政策下的人口结构预测

根据对1996-2015年总人口、劳动力人口结构、城镇人口结构、文化素质人口结构的数据统计，在不实施全面二孩政策的条件下，通过线性回归[7]和灰色预测[8]方法，分别画出总人口和各人口结构关于时间的变化如图1所示，图中圆点表示人口的实际值，曲线表示人口的预测值。

在实行一对夫妻只能生一个孩子的计划生育政策下，根据图形数据计算分析可得：

（1）劳动力人口占比略有降低，从2020年10.1亿人（占比71.63%）持续缓慢降至2025年9.9亿人（占比67.81%）和2030年9.6亿人（占比64.01%）。（2）城镇人口占比有小幅度增高，从 2020年 8.8亿人（占比62.41%）持续增至2025年9.9亿人（占比68.49%）和2030年11.1亿人（占比74.01%）。

（3）普通高等学校在校生人数占总人口的比重基本不变，2020年至2030年占比持续维持在2.16%到2.24%之间。

2.1.2 实施全面二孩政策下的人口结构预测

通过对“二孩政策”下社会生育比率的调整，运用Leslie模型对2020-2030年的各个人口结构指标进行预测[9]。本文假定全面实施二孩政策下的生育率为2.0，根据Leslie模型对2020-2030年人口规模及不同年龄结构人口数量进行预测，进而预测出2020-2030年总人口、劳动力、城镇人口结构以及人口文化素质结构变化趋势[10]。预测总人口和各人口结构关于时间的变化如图2所示。

在实行全面二孩政策下，根据图形计算分析可得：

（1）劳动力人口比重缓慢降低，与同期不实施全面二孩政策情况基本一致，但靠近2030年时，劳动力人口出现缓慢增高趋势;

（2）城镇人口比重持续增高，从2020年9.5亿人增至2030年13.4亿人;

（3）普通高校在校大学生人数缓慢增长，与同期不实施全面二孩政策情况基本一致。

图1 2020-2030年不实施全面二孩人口预测图Fig.1 Variation of population under Birth Control Policy from2020 to 2030

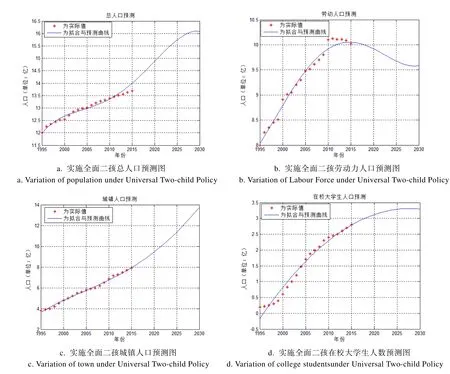
图2 2020-2030年实施二孩各种人口预测图Fig.2 Variation of population under universal Two-child policy from2020 to 2030

2.2 人口结构和经济发展的因果分析

由于人口劳动力结构、人口城乡结构及人口文化素质结构这三个方面的数据比较稳定，并且在很大程度上可以代表整体的人口结构，因此选择这三个方面作为人口结构的指标。人口劳动力结构用15-64岁人口在总人口中占的比重 X1(%)来表示，人口城乡结构用城镇人口占总人口的比重 X2(%)来表示，人口文化素质结构用普通高等学校在校生人数占总人口的比重 X3(%)来表示。反映经济增长的指标选用人均 G DP ( Y)。选取完指标之后，再对这些指标进行消除异方差的预处理。首先对所有指标取对数，记为 l nX1、 l nX2、 ln X3和lnY，用他们的一阶差分来表示增长率，可以建立模型：

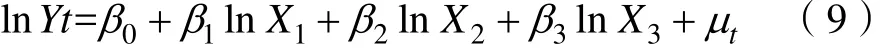
由于会有“伪回归”存在的情况，需要对指标lnX1、 ln X2、 ln X3和lnY的差分序列进行平稳性检验，本文采用ADF方法来进行[11]。借助E－Views软件得检验结果如图3所示。

根据软件显示的内容，对检验类型、ADF统计量、5%水平临界值等信息进行汇总统计，然后根据这些信息判断变量是否平稳。再根据变量的平稳性来进行协整检验。汇总检验结果参见表1。

从表1可以看出：序列1lnX、2lnX、3lnX和lnY都满足差分平稳序列的条件，因此可以进行单整的协整分析与检验。

本文在进行两个变量协整关系检验时用 EG两步检验法，然后在进行回归时用OLS法，结果如图4所示。

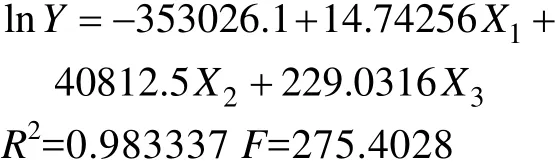
由于回归的DW=0.676654。须要在这个残差的基础上进行平稳性检验。

从上述方程可知，残差的估计值为:

然后对残差做单位根检验，结果如表2所示。

图3 ADF检验结果图Fig.3 ADF test result

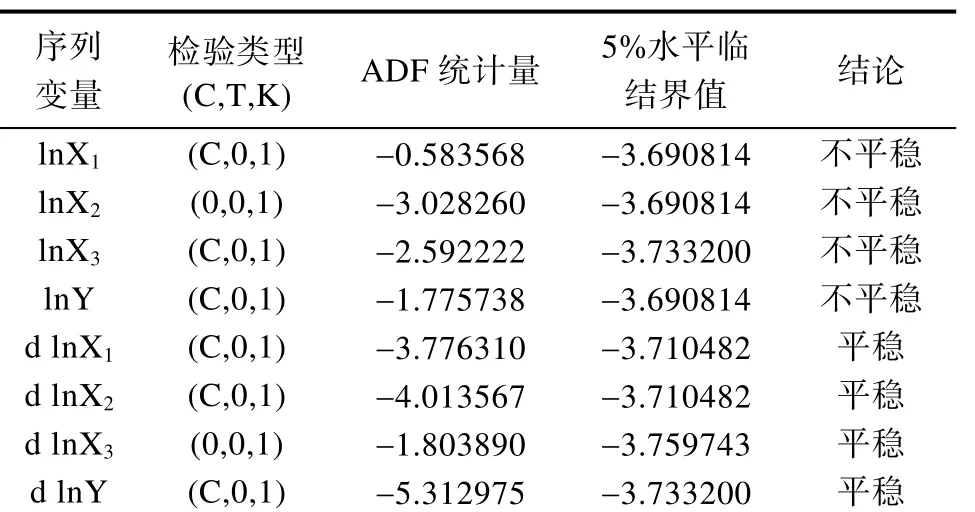
表1 各个序列变量的ADF检验结果Tab.1 ADF test result about sequence variable

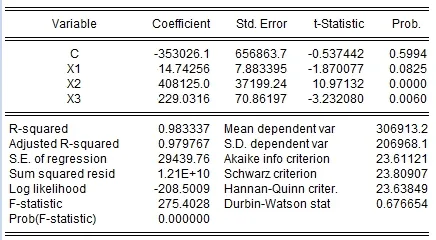
图4 回归方程结果图Fig.4 Regression equation results

表2 残差序列的ADF检验结果Tab.2 ADF test result about residual sequence

从表2可以看出：时间序列是协整的，可以进行下一步的检验。也就是说，本文选取的人口结构与人均GDP两者之间的时间序列是稳定的。从回归方程得出：长期来看，劳动力人口比重(1X)、城镇人口比重(2X)和普通高等学校在校大学生人口比重（3X）与经济增长呈正相关关系。

用Eviews进行Granger因果检验，结果如图5所示。

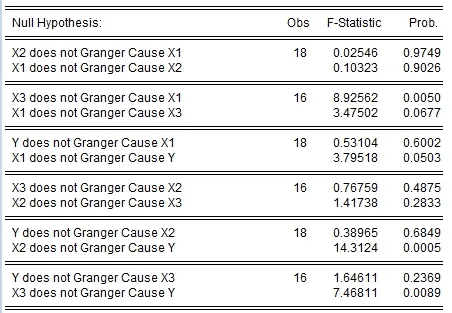
图5 Granger因果检验图Fig.5 Granger causality test

汇总结果如表3所示。

表3 Granger因果检验汇总表Tab.3 Summary about granger causality test

从表3可以看到：劳动力人口的比重(1X)、城镇人口的比重(2X)、普通高校在校大学生人口的比重(3X)都是经济变动的原因[12]。

通过对以上检验的分析，可得如下关系：

（1）劳动力人口和城镇人口都是影响人均GDP的原因，由双方的回归方程可知，两者都与人均GDP是一种正向关系。也就是说劳动人口和城镇人口比重均与经济增长存在正相关关系。

（2）普通高校在校生人数比重虽然是影响人均GDP的原因，但是影响程度不高，由回归方程可知，在校生人数与人均GDP有一种微弱的正向关系。也就是说，在校大学生人数的增多，在小幅范围内可以促进经济发展，但影响程度不高。

结合上述对人口结构的预测[13]可知：

如果不实施二孩政策，2020-2030年劳动力人口占比缓慢降低，阻碍经济的发展；同时城镇人口的小幅增高对经济发展具有推动作用；高校生比重不变，因此对经济发展影响不明显。

如果实施二孩政策，2020-2030年前期劳动力呈现缓慢降低的态势，但是后期劳动力人口比重明显增高，对经济发展具有促进作用；城镇人口大幅增加，推动经济的快速发展，但2030年左右开始呈现下滑趋势；高校生人口比重不变，对经济发展依然影响不大。

3 结论

根据以上结果，进行综合分析可得到以下结论：

（1）不实施全面二孩政策情况下，劳动力人口数量开始缓慢降低，人口结构出现老龄化趋势，导致经济无法维持较高较快的发展趋势。从2016年实施全面二孩政策到2030年，劳动力人口比重小幅降低但整体趋势平稳。但在2030年后，人口劳动力结构从降低逐渐转为增长，因此经济也将得到发展。

（2）不论是否实施全面二孩政策，城镇人口比重始终保持小幅度增长。但实施二孩政策后的 15年，城镇人口占比开始降低。也就是说，长远来看，持续开放二孩政策最终会导致城镇人口占比先增后减，乡村人口占比先减后增，最终会阻碍经济的发展。

通过以上分析，本文对我国人口政策提出如下建议：

在不同时期采取不同的生育政策。为使人口的发展更加科学合理，建议在开放全面二孩政策的20-30年后，逐步对社会的生育率进行限制（实施如单独二孩等政策），逐步降低生育率，这样才能保证经济持续稳定发展。

[1] 叶成绪, 郭超凡, 任竞尧, 凌应标, 张雨浓. 三次样条和二次删除相辅助的WASD神经网络与日本人口预测[J]. 软件, 2017, (6): 7-12.Ye C X, Guo C F, Ren J Y, Ling Y B, Zhang Y N; Cubic Spline and Double Deletion Assisted WASD Neural Network and Japanese Population Forecast [J], Software, 2017, (6):7-12.

[2] 李明来, 张梦宇, 张仪, 彭庆. 中国人口与经济发展关系探析与预测[J]. 经济研究导刊, 2017, (2): 1-2.Li M L, Zhang M Y, Zhang Y, Peng Q. An Analysis of the Relationship between Population and Economic Development in China[J]. Economic Research Guide, 2017, (2): 1-2.

[3] 杨新星, 李春青. 基于改进极限学习机的MBR仿真预测研究[J]. 软件, 2016, (12): 17-20.Yang X X, Li C Q. Research on MBR Simulation and Prediction Based on Improved Extreme Learning Machine[J].Software, 2016, (12): 17-20.

[4] 刘帅, 袁汝华. 基于Leslie矩阵的水资源供需平衡灰色预测研究[J]. 贵州师范大学学报(自然科学版), 2016, (1):22-27.Liu S, Yuan R H. Research on Gray Forecast of Water Resources Supply and Demand Balance Based on Leslie Matrix[J]. Journal of Guizhou Normal University (Science and Technology) 2016, (1): 22-27.

[5] 胡伟. 基于蒙特卡罗模拟实验的协整模型应用若干问题研究[D]. 北京: 北京邮电大学, 2015.Hu W. Research on Application of Cointegration Model Based on Monte Carlo Simulation Experiment [D]. Beijing:Beijing University of Posts and Telecommunications 015

[6] 刘华军, 何礼伟. 中国省际经济增长的空间关联网络结构——基于非线性Granger因果检验方法的再考察[J]. 财经研究, 2016, (2): 97-107.Liu H J, He L W. Spatial Correlation Network Structure of Inter-Provincial Economic Growth in China: A Re- examination Based on Nonlinear Granger's Causality Test [J]. Journal of Finance and Economics, 2016, (2): 97-107.

[7] 张哲来. 基于协同表示和线性回归的人脸识别算法研究[D]. 江苏: 苏州大学, 2015.Zhang Z L. Research on Face Recognition Algorithm Based on Cooperative Representation and Linear Regression [D].jiangsu: Soochow University, 2015.

[8] 刘运花, 黎雄, 刘志雄, 孙元章, 周歧林. 基于灰色预测的广域电力系统稳定器分布延时补偿设计[J]. 电力系统自动化, 2015, (12): 44-49.Liu Y H, Li X, Liu Z X, Sun Y Z, Zhou Q L. Delayed Design of Wide-area Power System Stabilizer Based on Gray Prediction [J]. Automation of Electric Power Systems, 2015,(12): 44-49.

[9] 陈友华. 全面二孩政策与中国人口趋势[J]. 学海, 2016, (1):62-66.Chen Y H. The universal Two-child Policy and China 's Demographic Trend [J]. Academia Bimestris, 2016, (1):62-66.

[10] 张月蓉. 中国天然气年消费量预测[D]. 辽宁: 东北财经大学, 2016.Zhang Y R. Forecast of China 's Natural Gas Consumption[D]. liaoning: Dongbei University of Finance and Economics,2016.

[11] 毛庆. 一带一路背景下西部地区旅游产业金融支持的实证分析——基于ADF检验和回归分析[J]. 新经济, 2016, (2):24.Mao Q. An Empirical Analysis of Financial Support for Tourism Industry in the Western Regional Belt and Road Backgroud - Based on ADF Test and Regression Analysis[J].New Economy, 2016, (2): 24.

[12] 郭凯明, 余靖雯, 龚六堂. 计划生育政策、城镇化与经济增长[J]. 金融研究. 2015 (11): 47-63.Guo K M, Yu Q W, Gong L T. Family planning policy, Urbanization and Economic growth[J]. Journal of Financial Research. 2015 (11): 47-63

[13] 史尤昭. 数据挖掘技术研究与应用[J]. 软件, 2015, (11):38-42.Shi Y S. Research and Application of Data Mining Technology[J]. Software, 2015, (11): 38-42.

A Study on the Effects of Population Structure on Economic Development Under the Universal Two-child Policy

HAN Lin-yi, WU Sheng, ZHOU Hai-he, LIU Ying-li, CUI Qing-fa
(School of Information Engineering and Automation, Kunming University of Science and technology, Kunming 650500, China)

China officially implemented the universal two-child policy since 2016. In order to assess the impact of demographic structure on economic development under the universal two-child policy. This paper is based on the Leslie model and the GM (1,1) model, and forecast the population and structure. And then doing unit root test and co-integration test about the population structure and per capita GDP, and on this basis for causal analysis. Finally,this paper compared between the population structure under the universal two-child policy and not the policy in 2017-2030, and causal analysis is used for comprehensive evaluation. The experimental results show that the credibility of the labor force population and the proportion of urban population have the influence are 0.68 and 0.60 in economic development. Moreover, the proportion of the labor force population and the urban population after the implementation of the universal two-child policy is greater than that before the implementation of the universal two-child policy. Concluded that under the influence of the universal two-child policy, China's economy will be improved from 2017 to 2030.

: Universal two-child; Leslie model; GM (1,1) Model; Causality test

TP391.4

A

10.3969/j.issn.1003-6970.2017.10.024

本文著录格式：韩林峄，吴晟，周海河，等. 全面二孩政策下人口结构对经济发展影响研究[J]. 软件，2017，38（10）：124-129

韩林峄(1992-)，男，硕士研究生，数据挖掘。

吴晟，教授，主要研究方向：数据挖掘，算法设计。