给定速度需求的移动机器人路径跟踪控制与实验

顾万里 胡云峰,2 宫 洵 蔡 硕 陈 虹,2

(1.吉林大学通信工程学院，长春 130025； 2.吉林大学汽车仿真与控制国家重点实验室，长春 130025；3.密歇根大学航空航天工程系，安娜堡 48105)

给定速度需求的移动机器人路径跟踪控制与实验

顾万里1胡云峰1,2宫 洵3蔡 硕1陈 虹1,2

(1.吉林大学通信工程学院，长春 130025； 2.吉林大学汽车仿真与控制国家重点实验室，长春 130025；3.密歇根大学航空航天工程系，安娜堡 48105)

针对轮式移动机器人给定速度需求的非连续路径跟踪控制问题，将其转换为满足速度约束的轨迹规划和轨迹跟踪控制。首先，针对给定速度需求的路径跟踪问题，以运行时间和能量为优化目标，给定的路径和速度为约束条件，采用五次Bezier样条方法优化得到了满足需求的连续光滑轨迹。其次，利用轮式移动人系统的微分平坦特性，采用微分平坦方法设计前馈控制器；然后，将轮式移动机器人运动学模型在前馈控制的平衡点处进行一阶泰勒展开，得到了线性时变的误差模型，并通过定义新的状态变量，设计了具有Lyapunov稳定性的误差反馈控制器。结合前馈控制和反馈控制得到了二自由度轨迹跟踪控制器。同时将泰勒展开的高阶项考虑为有界的扰动输入，在输入到状态稳定性框架下证明了控制系统的鲁棒稳定性；最后，通过Pioneer 3-dx轮式移动机器人进行了实验验证，实验结果表明，提出的算法能够满足给定速度需求的非连续路径的跟踪控制需求。

轮式移动机器人； 路径跟踪控制； Bezier样条； 微分平坦方法； Lyapunov方法

引言

随着移动机器人在航天[1]、工业[2]、农业[3-5]中的广泛应用，其轨迹跟踪问题受到越来越多人的关注。在实际应用中，移动机器人需准确、快速地跟踪上期望轨迹。但由于轮式移动机器人是一种典型的非完整约束系统，其高精度轨迹跟踪控制具有一定的难度[6]。

目前，针对非完整移动机器人的路径跟踪问题已有很多研究。文献[7-8]针对连续的期望路径，设计了基于非线性模型预测控制的路径跟踪控制器，该方法能够有效处理系统的约束，但是上述路径跟踪控制方法无法用于离散路径点跟踪控制问题；针对路径点的跟踪控制问题，主要是将其转换为轨迹规划和轨迹跟踪控制两部分。对于轨迹规划问题，早期的研究采用简单的直线、圆弧及回旋线来生成轨迹曲线，该方法简单、直观，但无法保证速度和加速度的连续性[9]。为此，文献[10-12]采用样条函数研究轨迹规划方法，克服了速度和加速度不连续的缺点。但是上述成果中均没有考虑给定的速度需求。对于轨迹跟踪控制问题，研究方法主要分成两方面，一方面是采用非线性控制方法设计控制器，比如滑模控制方法[13-14]、反步法[15]及反馈线性化方法[16]。但该类控制器结构复杂且设计过程繁琐，由此限制了上述方法的实际应用；另一方面是基于智能控制的轨迹跟踪控制器设计方法，比如神经网络方法[17]和迭代学习方法[18]等。该类方法可以在不知精确的机器人系统模型情况下，取得较好的控制效果，但是该算法对控制系统的计算能力要求极高，所以多数停留在仿真阶段。

综上，现有的轮式移动机器人路径跟踪控制方法仅是针对路径需求进行了研究，但是随着轮式移动机器人应用场景的不断扩大，不仅对路径点有要求，也对通过路径点的速度提出了要求[19]，但目前还鲜有这方面的研究成果。本文针对包含给定速度和位置需求的离散路径点的轮式移动机器人跟踪控制问题，设计基于五次Bezier样条的轨迹规划方法，以及前馈和反馈相结合的二自由度轨迹跟踪控制器，并采用Lyapunov方法分析闭环误差系统的稳定性及鲁棒性。

1 问题描述

轮式移动机器人模型如图1所示。后轮为2个差动驱动轮，前轮为1个起支撑作用的万向随动轮。其中，驱动中心和质心重合在P点，(x,y)为机器人的位置坐标，后轮直径为2r，间距为2b，θ为机器人的位姿角，ω为以垂直轴Z为转动中心的转动角速度，v为机器人运动过程中的瞬时线速度。

图1 轮式移动机器人模型Fig.1 Model of wheeled mobile robot

轮式移动机器人系统为典型的非完整约束系统，其非完整约束包含2个含义：①机器人不能够侧向滑移。②机器人前进时，轮子与地面之间满足纯滚动无滑动的约束条件。轮式移动机器人运动学方程为

(1)

轮式移动机器人给定速度需求的路径规划及跟踪控制问题可以描述为：对于如图2所示的给定速度需求的路径点W(x*,y*,v*)，设计路径跟踪控制方法使式(1)的实际轨迹能够通过期望的路径点(x*,y*)，并且通过该路径点的速度为v*。为此，本文设计了如图3所示的控制方案。首先，设计了轨迹规划算法，根据期望的给定速度需求的路径点W(x*,y*,v*)生成与时间相关的连续光滑的期望轨迹(xd(t),yd(t))；然后，设计前馈和反馈相结合的二自由度轨迹跟踪控制器，实现对期望的给定速度需求的路径点的精确跟踪控制。

图2 给定速度需求的期望路径点Fig.2 Discontinuous path with given velocity requirement

图3 控制方案Fig.3 Control strategy

2 基于Bezier样条的轨迹规划

基于离散的给定速度需求的路径点P(x*,y*,v*)，生成与时间相关的光滑的轨迹(xd(t),yd(t))。为了让移动机器人能够精确跟踪参考轨迹，生成的轨迹须满足曲率连续。因此采用五次Bezier样条曲线对轨迹进行参数化。

假设给定路径点的个数为n+1，由W{(xi,yi,vi),i=0,1,2,…,n}所示。将任意的相邻路径点(Wi,Wi+1)之间的时间归一化为1 s，则相邻路径点(Wi,Wi+1)之间的曲线fi(t)的表达式为

fi(t)=(1-t)5Pi,0+5(1-t)4tPi,1+10(1-t)3t2Pi,2+
10(1-t)2t3Pi,3+5(1-t)t4Pi,4+t5Pi,5

(2)

式中Pi,0、Pi,5——控制轨迹形状参数

Pi,1、Pi,4——控制轨迹速度参数

Pi,2、Pi,3——控制轨迹加速度参数

针对该参数化轨迹，可以将路径规划问题转换为非线性优化问题，即

其中

式中f(P,H)——优化目标函数，可以选择为时间、能量或者冲击量

P——优化参数H——优化参数

hi——相邻路径点间的实际运行时间

fvi(t)——根据轨迹表达式fi(t)求得的速度

fai(t)——根据轨迹表达式fi(t)求得的加速度

最后，对该非线性优化问题进行求解就可以得到满足需求的轨迹。该轨迹规划过程共分为3步：

(1)选择5次Bezier样条曲线对轨迹进行参数化，参数分为：控制轨迹形状的参数P和调节各路径点之间时间的参数H。

(2)将轨迹规划问题转换为非线性优化问题，优化目标函数可以选择为时间、能量或者冲击量。约束条件为对应路径点的位置和速度，且满足加速度连续条件。

(3)求解该非线性优化问题(如Matlab自带的fmincon函数)。

3 二自由度轨迹跟踪控制器设计

3.1 前馈控制器设计

基于微分平坦技术设计了前馈控制器。但在实际过程中，由于系统数学模型不可能完全精确，总会存在不确定性和内外部扰动，在参考轨迹附近，对模型进行线性化，针对得到的误差模型，设计了反馈控制器，并在Lyapunov稳定性框架下证明了闭环误差系统的稳定性。

由于轮式移动机器人系统是微分平坦系统[21]，因此，可以通过选取合适的平坦输出将系统所有的状态变量和输入变量用平坦输出及其有限阶导数表示。这里选取平坦输出

z=(x,y)

(3)

结合轮式移动机器人的运动学模型(1)经简单推导得

(4)

由于轮式移动机器人系统的状态和输入可由平坦输出及其有限阶导数表示，进而可以由期望轨迹(xd(t),yd(t))得到前馈控制率为

(5)

3.2 反馈控制器设计

首先将轮式移动机器人模型在前馈控制的平衡点处进行一阶泰勒展开，得到跟踪误差系统，进而设计了误差反馈控制器，并在Lyapunov稳定性框架下证明了闭环系统的稳定性。

定义反馈控制输入为Δv=v-vf,Δω=ω-ωf，以及系统控制偏差为xe=x-xd,ye=y-yd,θe=θ-θy。将系统(1)在(xd,yd,vf,θf,ωf)点处进行一阶泰勒展开得

(6)

式中dx、dy——泰勒展开的高阶项，将其考虑成建模误差

设计控制器的过程中先不考虑建模误差项，结合式(1)和式(6)，进一步整理可得

(7)

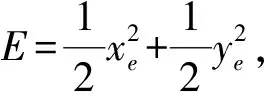
(-vfsinθfxe+vfcosθfye)θe

(8)

由式(8)可知，如果能证明E收敛于0，即可证明xe、ye收敛于0，因此，通过上述变量，将xe、ye2个变量的收敛性问题转换为一个变量E的收敛性问题。

为了证明误差系统(7)的稳定性，定义Lyapunov函数

(9)

对式(9)两端进行求导，并将式(7)、(8)代入可得

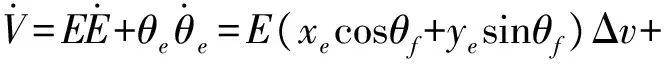
(10)

为了证明误差系统的稳定性，取

(11)

将式(11)代入式(10)整理可得

(12)

式中k1、k2——控制器参数

由式(12)可知，当选择k1>0,k2>0时，有

(13)

并且式(13)只在原点处等于零，因此，可以得到E、θe可以渐进收敛于0，即可得到xe、ye、θe收敛于0。

上述过程证明了在忽略系统建模误差时，闭环误差系统具有渐进稳定性，但是系统中存在泰勒展开的高阶项等建模误差，因此，需要进一步证明，闭环系统存在扰动情况下的鲁棒稳定性。

3.3 鲁棒稳定性分析

在以上控制器设计过程中，由于未考虑建模误差，本节将建模误差考虑成幅值有界的扰动，在输入到状态稳定性理论框架下，证明了闭环误差系统的鲁棒性。

包含建模误差的误差动力学方程为

(14)

为了证明其闭环系统的鲁棒性，本文将包含建模误差的式(14)代入到式(9)定义的Lyapunov函数导数方程中，得到

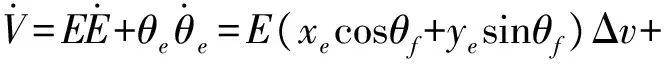
(15)

将控制输入式(11)代入到式(15)，得到

(16)

为此，对式(16)右端使用Young’s不等式可得

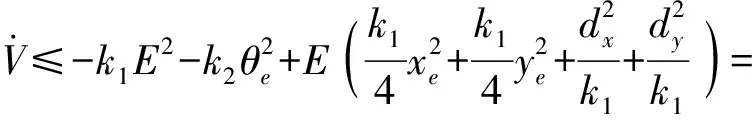
因此，由输入到状态稳定性理论可知，系统从扰动输入dx、dy到状态E、θe具有稳定性，即具有鲁棒稳定性。

4 实验与分析

图4 Pioneer 3-dx实物图Fig.4 Photo of Pioneer 3-dx

为了验证本文所提出的算法有效性，在Mobilerobots公司开发的Pioneer 3-dx实验平台上对该算法进行了实验验证。该平台实物如图4所示。Pioneer 3-dx机器人以客户端—服务器模式运行。客户端采用PC实现，用于运行Windows程序和基于C++编写的用户应用程序。服务器端基于DSP实现，用于执行移动机器人底层控制，包括速度控制及采集传感器信息。客户端和服务器端采用串口进行通讯。该移动机器人主要参数如表1所示。

表1 Pioneer 3-dx机器人参数Tab.1 Parameters of Pioneer 3-dx

在实验过程中，首先基于Pioneer 3-dx机器人PC客户端运行的Matlab软件编写了轨迹规划程序，对于步骤3中的优化函数选择为fmincon函数，由此得到了期望的运行轨迹。然后，基于Mobilerobots公司开发的ARIA控制接口库，在VS2010编译器下采用C++编写了轨迹跟踪控制程序。

针对本文所设计算法，给出以下两种路径用于进行实验验证。

(1) 路径点的跟踪控制

以路径点W0=[(0,0,0.18);(0.6,0.1,0.30); (1.8,0.6,0.50); (3.0,0.9,0.60); (5.0,1.0,0.30); (5.8,0.6,0.10)]和W1=[(0,0,0.18); (0.6,0.1,0.30); (1.5,0.5,0.50); (2.6,1.5,0.60); (3.9,3.5,0.50); (5.0,6.0,0.10)]为例，来验证本文算法的有效性。

对于路径点的跟踪控制，首先需要进行轨迹规划，采用前文基于Bezier样条的轨迹规划方法进行轨迹规划，对于得到的期望轨迹，其Bezier样条参数如下：

针对路径点W0规划得到的轨迹，对应的五次Bezier样条曲线的参数为

针对路径点W1规划得到的轨迹，对应的五次Bezier样条曲线的参数为

由此得到规划的参考轨迹和期望的路径及速度对比曲线如图5～8所示。

图5 路径点W0规划得到的x和y方向轨迹Fig.5 Generated reference trajectories for waypoints W0 in x and y directions

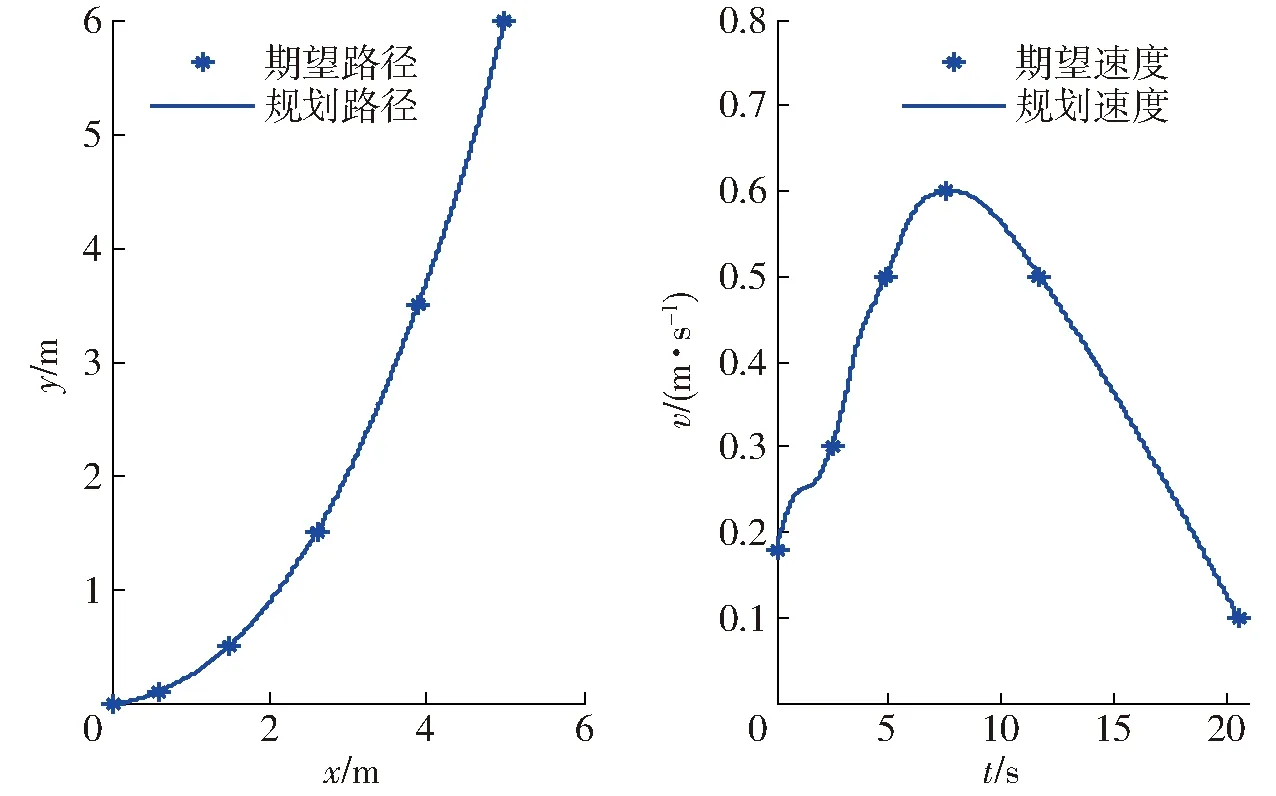
图6 路径点W0规划路径和速度与参考值对比Fig.6 Comparison of generated reference trajectory and reference value for waypoints W0

由图5～8可看出，采用该方法规划得到的轨迹能够精确经过期望的路径点。

以图5和图7中的轨迹作为跟踪实验的参考轨迹，采用推导的轨迹跟踪算法进行轨迹跟踪实验，对于路径点W0初对应的始偏差分别选择为(0,0,0)和(0.6,0.3,0)。对于路径点W1初对应的始偏差分别选择为(0,0,0)和(1.0,1.0,0)。其实验结果如图9～12所示。

图7 路径点W1规划得到的x和y方向轨迹Fig.7 Generated reference trajectories for waypoints W1 in x and y directions

图8 路径点W1规划路径和速度与参考值对比Fig.8 Comparison of generated reference trajectory and reference value for waypoints W1

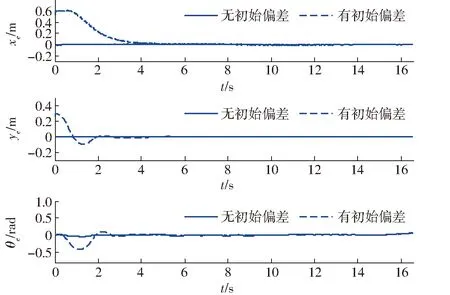
图9 路径点W0跟踪误差Fig.9 Tracking errors for waypoints W0

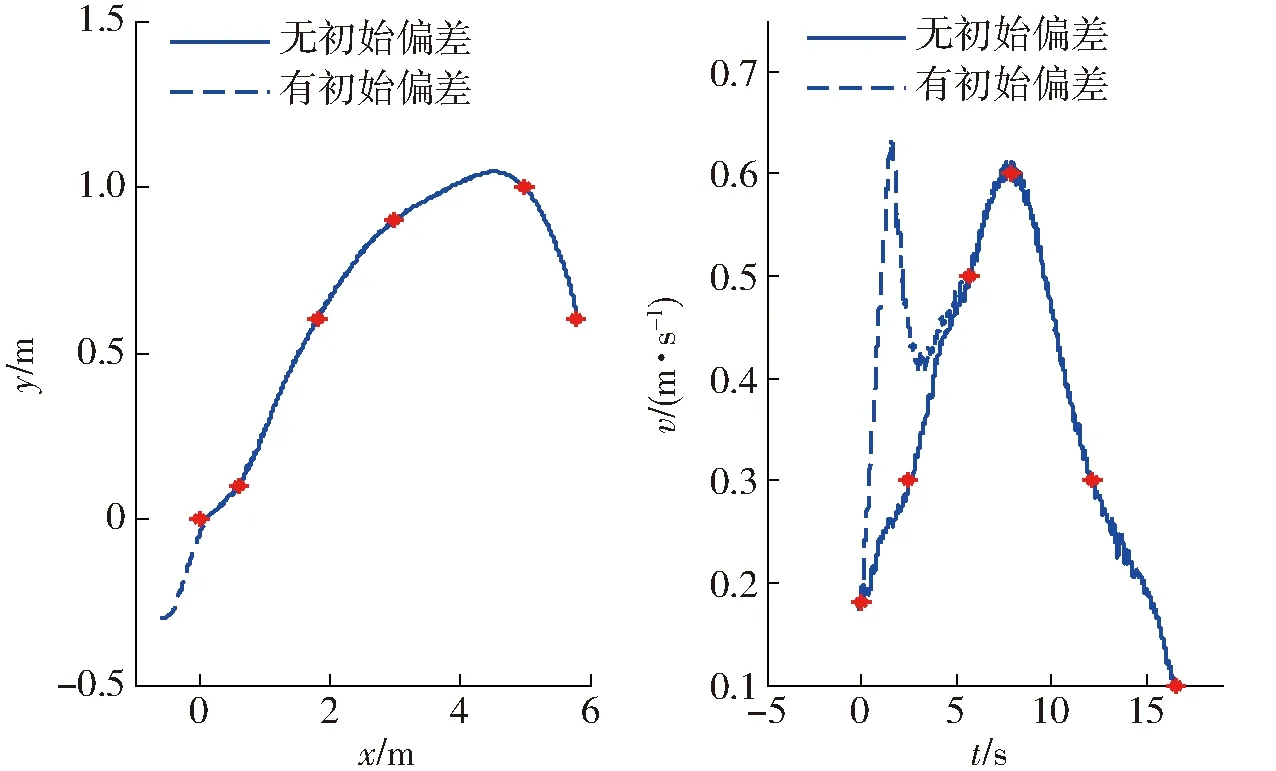
图10 路径点W0实际路径和速度与参考值对比Fig.10 Comparison of real path and velocity with reference value for waypoints W0

由图9～12可得，在没有初始偏差情况下，该控制器能够很好跟踪上期望轨迹。在有初始偏差情况下，该控制器能够很快收敛到期望轨迹。

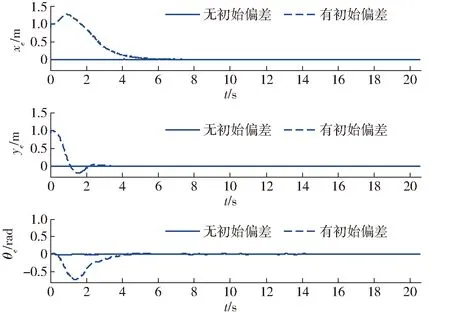
图11 路径点W1跟踪误差Fig.11 Tracking errors for waypoints W1

图12 路径点W1实际路径和速度与参考值对比Fig.12 Comparison of real path and velocity with reference value for waypoints W1

(2) 圆轨迹跟踪控制

其参考轨迹为

采用推导的轨迹跟踪算法进行轨迹跟踪实验，初始偏差分别选择为(0,0,0)和(0.6,0.6,0)。其实验结果如图13、图14所示。

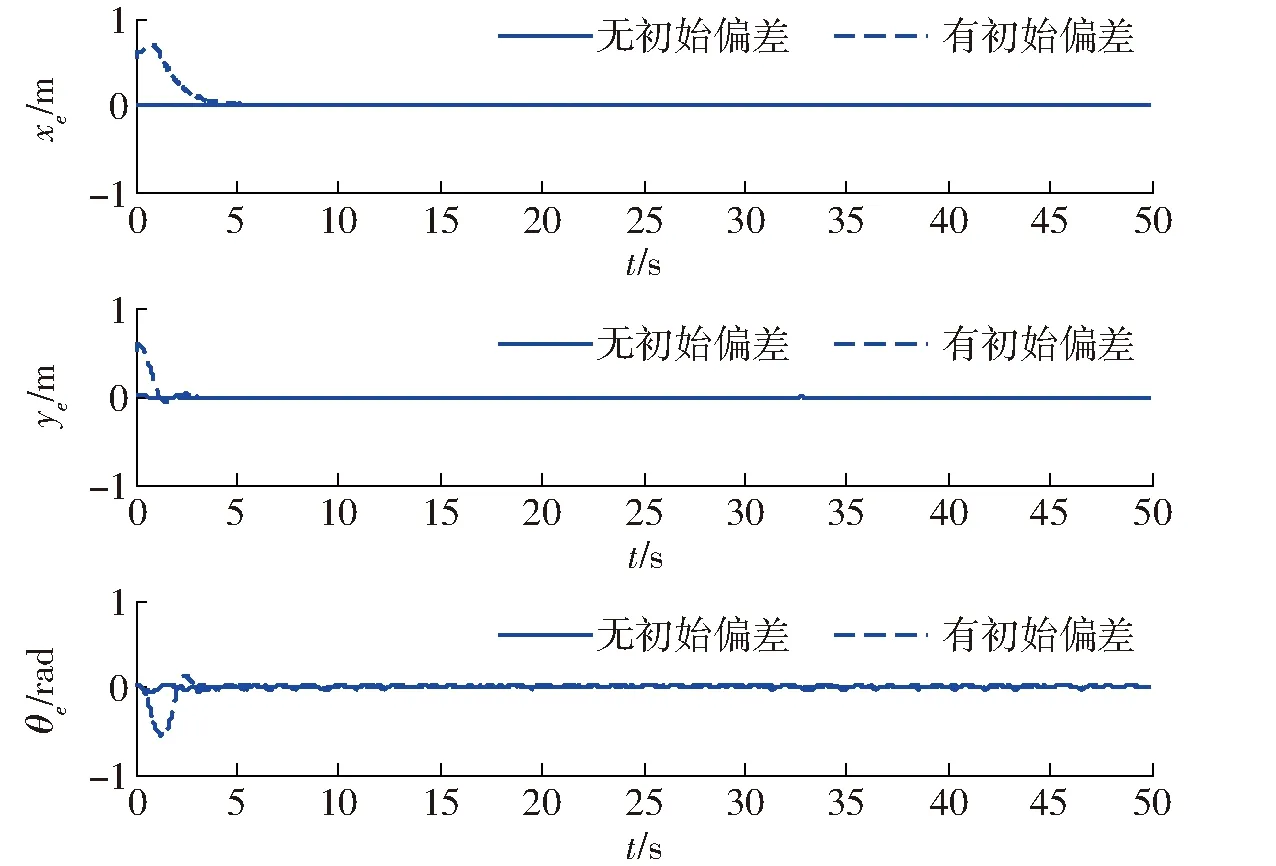
图13 跟踪误差Fig.13 Tracking errors

由图13、图14可以得到，在没有初始偏差情况下，该控制器能够很好跟踪上期望的轨迹。在有初始偏差情况下，该控制器能够很快收敛到期望的轨迹。

5 结束语

研究了给定速度需求的路径点跟踪控制问题。首先,设计了能够满足速度需求的基于Bezier样条优化的轨迹规划方法。针对规划得到的轨迹，设计了具有前馈和反馈结构的轨迹跟踪控制器，对其进行跟踪控制。结果表明，本文设计的轨迹规划方法能够满足精确的速度需求，且设计的轨迹跟踪控制器可以使系统跟踪上该轨迹，从而完成了整个运动控制。

图14 实际路径和速度与参考值对比Fig.14 Comparison of real path and velocity with reference value

1 SUTOH M, OTSUKI M, WAKABAYASHI S, et al.The right path: comprehensive path planning for lunar exploration rovers [J].IEEE Robotics & Automation Magazine, 2015, 22(1): 22-33.

2 CEN Y, SONG C, XIE N, et al.Path planning method for mobile robot based on ant colony optimization algorithm[C]∥3rd IEEE Conference on Industrial Electronics and Applications.ICIEA, Iciea, 2008: 298-301.

3 赵源深, 贡亮, 周斌,等.番茄采摘机器人非颜色编码化目标识别算法研究[J/OL].农业机械学报, 2016, 47(7):1-7.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160701&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.07.001.

ZHAO Yuanshen, GONG Liang, ZHOU Bin, et al.Object recognition algorithm of tomato harvesting robot using non-color coding approach [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(7):1-7.(in Chinese)

4 钱晓明, 张浩, 王晓勇,等.基于激光扫描匹配的移动机器人相对定位技术研究[J/OL].农业机械学报, 2016, 47(3):14-21.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160303&journal_id=jcsam.DOI:10.6041/ j.issn.1000-1298.2016.03.003.

QIAN Xiaoming, ZHANG Hao, WANG Xiaoyong, et al.Relative localization technology for mobile robot based on laser scan matching [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3):14-21.(in Chinese)

5 褚佳, 张立博, 张铁中,等.葫芦科穴盘苗单人操作嫁接机器人设计与试验[J/OL].农业机械学报, 2017,48(1):7-13.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170102&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2017.01.002.

CHU Jia, ZHANG Libo, ZHANG Tiezhong, et al.Design and experiment of grafting robot operated by one person for cucurbitaceous seedlings cultivated in plug trays[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2017,48(1):7-13.(in Chinese)

6 BOMG S P, SUNG J Y, JIN B P, et al.A simple adaptive control approach for trajectory tracking of electrically driven nonholonomic mobile robots [J].IEEE Transactions on Control Systems Technology, 2010, 18(5): 1199-1206.

7 YU S, LI X, CHEN H.Nonlinear model predictive control for path following problems [J].International Journal of Robust and Nonlinear Control, 2015, 25(8): 1168-1182.

8 刘洋.基于模型预测控制的移动机器人路径跟踪控制[D].长春：吉林大学,2016.

LIU Yang.Nonlinear model predictive control for path-following problems of wheeled mobile robots [D].Changchun:Jilin University, 2016.(in Chinese)

9 KOMORIYA K, TANIE K.Trajectory design and control of a wheel-type mobile robot using B-spline curve[C]∥Intelligent Robots and Systems’89.The Autonomous Mobile Robots and Its Applications.IROS’89.Proceedings, IEEE/RSJ International Workshop on IEEE, 1989: 398-405.

10 GASPARETTO A, ZANOTTO V.Optimal trajectory planning for industrial robots[J].Advances in Engineering Software, 2010, 41(4): 548-556.

11 KUCUK S.Maximal dexterous trajectory generation and cubic spline optimization for fully planar parallel manipulators[J].Computers & Electrical Engineering, 2016, 56: 634-647.

12 BHARATHI A, DONG J.Feedrate optimization for smooth minimum-time trajectory generation with higher order constraints[J].The International Journal of Advanced Manufacturing Technology, 2016, 82(5-8): 1029-1040.

13 QIAN D, TONG S, LI C.Leader-following formation control of multiple robots with uncertainties through sliding mode and nonlinear disturbance observer[J].ETRI Journal, 2016, 38(5): 1008-1018.

14 QIAN D, LI C, TONG S, et al.Integral sliding mode-based formation control of multiple unertain robots via nonlinear disturbane observer[J].International Journal of Advanced Robotic Systems, 2016, 13(6): 1-11.

15 CHWA D.Robust distance-based tracking control of wheeled mobile robots using vision sensors in the presence of kinematic disturbances[J].IEEE Transactions on Industrial Electronics, 2016, 63(10):6172-6183.

16 LUVIANO-JUREZ A, CORTS-ROMERO J, SIRA-RAMREZ H.Trajectory tracking control of a mobile robot through a flatness-based exact feedforward linearization scheme[J].Journal of Dynamic Systems, Measurement, 2015, 137(5): 051001.

17 YE J.Tracking control of a non-holonomic wheeled mobile robots using improved compound cosine function neural networks [J].International Journal of Control, 2015, 88(2): 364-373.

18 LU X, FEI J.Velocity tracking control of wheeled mobile robots by iterative learning control [J].International Journal of Advanced Robotic Systems, 2016, DOI: 10.5772/63813.

19 孙施浩,赵林,贾英民.空间合作目标运动再现的相似设计方法研究[J].宇航学报, 2014, 35(7): 802-810.

SUN Shihao, ZHAO Lin, JIA Yingmin.Similitude design method for motion reconstruction of space cooperative vehicles [J].Journal of Astronautics, 2014, 35(7): 802-810.(in Chinese)

20 余伶俐, 龙子威, 周开军.基于贝塞尔曲线的机器人非时间轨迹跟踪方法[J].仪器仪表学报, 2016, 37(7): 1564-1572.

YU Lingli, LONG Ziwei, ZHOU Kaijun.Non-time trajectory tracking method based on Bezier curve for robot[J].Chinese Journal of Scientific Instrument, 2016,37(7):1564-1572.(in Chinese)

21 WALSH G, TILBURY D, SASTRY S, et al.Stabilization of trajectories for systems with nonholonomic constraints [J].IEEE Transactions on Automatic Control, 1994, 39 (1): 216-222.

PathTrackingControlandExperimentsforWheeledMobileRobotswithGivenVelocityRequirement

GU Wanli1HU Yunfeng1,2GONG Xun3CAI Shuo1CHEN Hong1,2

(1.CollegeofControlScienceandEngineering,JilinUniversity,Changchun130025,China2.StateKeyLaboratoryofAutomotiveSimulationandControl,JilinUniversity,Changchun130025,China3.DepartmentofAerospaceEngineering,MichiganUniversity,AnnArborMI48105,USA)

For the discontinuous path tracking problem of wheeled mobile robots with given velocity requirement, it was transformed into the trajectory planning and trajectory tracking problems.Firstly, for the given position and velocity requirements, quintic Bezier curve was used to parameterize the trajectory.Then the trajectory planning problem was transformed into the nonlinear optimization problem, for which the energy and interval times were selected as the optimization objective to optimize the parameterized trajectory.By solving the nonlinear optimization problems, a continuous and smooth trajectory was generated, which satisfied the given position and velocity requirements.Secondly, by exploiting the differential flatness properties of the wheeled mobile robots system, a feedforward controller was designed by using the differential-flatness approach.Thirdly, the kinematic model of the wheeled mobile robots was linearized at its equilibrium point of the feedforward control by using the first order Taylor expansion.Then, an linear time-varying error model was deduced.By defining a new error variable, a feedback controller was designed and the stability of closed loop error system was proved in the Lyapunov framework.Therefore, a two degree of freedom trajectory tracking controller was given.This method had the advantages of simple structure and clear engineering significance.In addition, the higher order terms of the Taylor series were considered as a bounded disturbance input, and the robustness of the system was discussed in the framework of input to state stability theory.Finally, the effectiveness of the proposed trajectory planning and trajectory tracking methods was validated on the Pioneer 3-dx wheeled mobile robot experiment platform.It can be seen from the experimental results that the proposed methods can track the discontinuous path with the given velocity requirement precisely.

wheeled mobile robot; path tracking control; Bezier curve; differential-flatness approach; Lyapunov method

10.6041/j.issn.1000-1298.2017.10.003

TP273

A

1000-1298(2017)10-0025-07

2017-05-18

2017-07-21

国家自然科学基金重点项目(61520106008、61374046)

顾万里(1988—)，男，博士生，主要从事非线性控制系统设计研究,E-mail: guwl13@mails.jlu.edu.cn

胡云峰(1983—)，男，副教授，主要从事非线性控制应用及汽车电子控制研究,E-mail: huyf@jlu.edu.cn