基于柔性多体动力学的机械臂结构优化设计
梁明轩 李正刚 唐任仲 陈 立 黄 川
1.浙江大学机械工程学院, 杭州,3100272.杭州新松机器人自动化有限公司, 杭州,310000 3. 中国计量大学机电工程学院, 杭州,310018
基于柔性多体动力学的机械臂结构优化设计
梁明轩1,2,3李正刚2唐任仲1陈 立2黄 川2
1.浙江大学机械工程学院, 杭州,3100272.杭州新松机器人自动化有限公司, 杭州,310000 3. 中国计量大学机电工程学院, 杭州,310018
针对柔性关节对工业机器人动力学特性的影响,基于“转子-扭簧”模型和有限元法,研究关节刚度对机械臂固有动力学特性的影响规律;考虑臂杆柔性和关节柔性,建立了机械臂多柔体动力学有限元模型,以机械臂轻量化为设计目标,以末端总位移量为约束条件对机械臂结构进行优化。研究结果表明,不同关节刚度对机械臂各阶固有频率的影响不同,优化后的机械臂载重/自重比增大,刚度和强度均得到提高,整体动力学性能明显提高。
机械臂;关节刚度;柔性多体动力学;拓扑优化;载重/自重比
0 引言
机械臂是工业机器人主要支撑与执行部件,载重/自重比是衡量其动作性能的重要指标,相对国外机械臂,国产机械臂载重/自重比较小,末端承载能力低,因而研究机械臂动态性能优化对提高国产机器人载重/自重比和末端操作精度具有重要意义[1]。机械臂过于轻量化往往会引起各部件产生较大的弹性变形及末端振动,在机器人的自重和外部负载的作用下,变形会累积到机器人的末端,引起末端的定位误差[2]。在某些对末端定位精度要求高的场合,弹性作用不能忽略[3]。在机械臂动力学性能分析和优化时,必须考虑机器人系统柔性环节的影响。
针对机械臂柔性关节引起的末端振动,国内外已有很多关于柔性关节建模的研究,例如SPONG[4]首次采用“转子-扭簧系统”模型来模拟柔性关节作用。在此基础上,BAHRAMI等[5]建立了“线性扭簧-阻尼”模型,使之成为柔性关节力学建模的首选。有些学者同时考虑了臂杆柔性和关节柔性、间隙等因素,采用拉格朗日方程和假设模态法建立机械臂系统的简化模型,这对于机械臂非线性振动特性分析至关重要,但在实际机械臂优化中还很少应用[6-7]。目前许多对机械臂的结构优化主要将机械臂关节看成刚性的,且是针对某一个零件在模拟载荷下的结构改进,忽略了各部件之间的耦合作用关系,对考虑臂杆柔性和关节柔性的机械臂结构优化有待深入研究。
本文以某型国产六自由度机械臂本体初始设计模型为对象,研究机械臂关节柔性和负载质量对机械臂动力学特性的影响;结合多柔体动力学、有限元法和结构拓扑优化理论,以机械臂轻量化为设计目标,开展机械臂关键部件结构优化设计。
1 柔性关节对动力学特性的影响分析
机械臂弹性变形主要有臂杆变形和关节变形,关节变形主要是由传动件如谐波减速器、传动带等产生的。为了分析关节柔性对机械臂整体动力学性能的影响,采用“线性扭簧-阻尼”模型表示关节柔性特性。用Δθ表示关节相对扭转角,则关节扭矩可以表示为τ=KΔθ,其中,K表示关节综合扭转刚度,可由谐波减速器的扭转刚度近似代替[8]。机械臂末端手腕关节柔性对动力学性能影响较小,把手腕关节设成固定副,仅考虑腰关节、大臂关节和肘关节等关节柔性的影响。
基于机械臂初始三维设计模型建立底座、腰部、大臂、肘部、小臂以及手腕等关键部件有限元模型,如图1所示。有限元网格模型共有1 341 036个四面体单元和336 870个节点。柔性臂杆材料为浇铸铝合金,密度为2700 kg/m3,弹性模量为72 GPa,泊松比为0.3。机械臂工作过程中形位姿态不断变化,不同形位姿态下结构质量分布和承载能力不同,本文选取机械臂处于水平最大臂展位置这一危险姿态进行分析。在底座4个螺栓孔建立螺栓预紧单元,采用block lanczos法提取不同关节刚度下机械臂前五阶模态。图2和图3所示分别为腰关节扭转刚度和大臂关节扭转刚度对机械臂前五阶固有频率的影响规律。

(a)实体模型

(b)有限元模型图1 机械臂实体模型和有限元模型Fig.1 The solid model and finite element model of robot arm

图2 腰关节刚度的影响Fig.2 Effect of waist joint stiffness

图3 大臂关节刚度的影响Fig.3 Effect of upper arm joint stiffness
当考虑腰关节柔性时,机械臂前三阶振型均含有腰部扭转振动,前三阶固有频率受腰关节扭转刚度的影响较大,从图2中可以看出,当腰关节扭转刚度小于0.3 MN·mm/(°)时,机械臂前三阶固有频率会随着腰关节刚度的增大而明显增大,当扭转刚度大于0.3 MN·mm/(°)时,腰关节刚度变化对前三阶固有频率的影响相对减弱;第四、五阶固有频率受腰关节柔性的影响较小。由于第二阶振型主要为机械臂左右摆动振动,该振型与大臂关节的扭转方向无关,从图3也可以发现,大臂关节刚度对第二阶频率没有影响;当大臂关节刚度大于0.3 MN·mm/(°)时,对第一、三、四阶固有频率的影响并不明显,但当该刚度在0.01~0.3 MN·mm/(°)范围内时,第一、三、四阶固有频率随着该关节刚度的增大而增大;由于第五阶振型为大臂与腰部连接处的相对扭转,该阶固有频率会随着大臂扭转刚度的增大而持续增大。

图4 肘关节刚度的影响Fig.4 Effect of elbow joint stiffness
图4所示为肘关节扭转刚度对机械臂固有频率的影响规律,考虑肘关节柔性时,机械臂第五阶振型为肘关节与大臂连接处的相对扭转,肘关节刚度对第五阶固有频率影响较大,但对第一、二阶频率没有影响。当肘关节刚度小于50 kN·mm/(°)时,第三、四阶频率会随着肘关节扭转刚度的增大而增大,但当该刚度大于50 kN·mm/(°)时,第三、四阶频率变化很小。以上分析结果表明,不同部位的关节刚度变化对机械臂各阶固有频率的影响不同,关节刚度的增大会使相应固有频率提高,腰关节刚度主要影响与腰部扭转有关的机械臂侧方向摆动固有频率,大臂关节主要影响机械臂末端上下振动频率,肘关节主要影响肘部弯曲振动频率。由此可知,在对机械臂结构进行优化时,必须考虑各关节刚度的影响,建立机械臂多柔体耦合优化模型。
2 多柔体机械臂结构优化设计
为了提高机械臂载重/自重比,笔者针对机械臂初始设计进行结构优化设计,在满足机械臂末端承载能力的前提下,减小机械臂本体质量和部件运动惯量,提高动力学性能。结构拓扑优化通常以有限元理论为基础,在优化模型中,利用各向同性固体材料惩罚函数法(SIMP),以优化区域内每个单元的密度作为设计变量,将结构的拓扑优化问题转换为单元材料的最优分布问题,引入插值惩罚因子来描述弹性模量E与单元密度xe的关系[9]:
E=(xe)pE0
(1)
其中,e为单元序号;p为惩罚因子,p>1;E0为致密化单元实体材料弹性模量;E为插值以后的单元空洞单元的弹性模量。同理,初始单元刚度k0和插值后的单元刚度k的关系可以表示为
k=(xe)pk0
(2)
初始单元密度ρ0和插值后的单元密度ρ的关系可以表示为
ρ=xeρ0
(3)
若以机械臂结构柔度的最小化(即刚度最大化为目标),则基于有限元法的拓扑优化数学模型为

(4)
s.t.F=KU
0 式中,C为机械臂结构总柔度;x为单元设计变量;U为位移向量;ue为单元位移向量;F为载荷向量;n为机械臂结构优化区域内总单元体数量;M0为机械臂结构初始质量;xmin为防止总体刚度矩阵奇异而设定的密度下限,通常取一极小的正数。 该优化模型以优化区域内单元的相对密度作为拓扑优化设计变量,这样结构的拓扑优化问题就转换为材料的最优分布问题。依据各关节谐波减速器实际型号,在腰部关节处建立扭转刚度为31 kN·mm/(°)的扭转弹簧单元,在大臂关节和肘关节建立扭转刚度为16 kN·mm/(°)的扭转弹簧单元,各关节阻尼比取0.8。在底座螺栓孔处建立螺栓预紧单元,模拟底座螺栓约束,末端手腕关节采用固定副连接。在机械臂末端竖直方向和水平方向施加额定力载荷40 N,绕机械臂轴向方向施加额定力矩载荷50 N·m。由静力学分析得到机械臂末端最大位移为1.5 mm,最大应力位于腰部,为6.2 MPa,远远小于臂杆材料的屈服强度217 MPa,则该机械臂具有足够的强度裕度,优化过程中主要考虑刚度约束。 本文主要针对大臂、肘部和小臂结构进行优化,各部件可优化区域如图5所示。以机械臂可优化区域内材料最少为设计目标,以机械臂末端总位移小于1.5 mm为约束条件,考虑机械臂自身重力和末端负载的影响,对机械臂进行拓扑优化,经过25次迭代得到机械臂单元相对密度云图,如图6所示。 图5 优化区域分布Fig.5 Distribution of optimized area 图6 机械臂单元相对密度云图Fig.6 Element density nephogram of robot arm 在密度云图中数值代表相对于初始模型密度比值,相对密度值越接近1的区域材料去除越少,越接近0.01的区域材料可以去除越多,根据优化结果,考虑机械臂各部件铸造工艺约束,对大臂、小臂和肘部的初始模型进行改进设计,具体优化部位如图7所示。 (a)初始三维设计模型 (b)优化后三维设计模型图7 优化前后设计模型对比Fig.7 Comparison of design model 优化的机械臂总质量为12.4 kg,相对初始设计质量减小5%,机械臂载重/自重比由0.30提高到0.32。为了验证优化设计的合理性,对优化后的机械臂动重新进行静力学分析,得到优化后的机械臂在额定负载下的总应力云图和变形云图,如图8所示。 从图8可以看出,优化后的机械臂在前述额定工况下的最大应力为5.5 MPa,最大应力位于机械臂腰部,相对于优化前的机械臂该应力有所减小;机械臂末端的最大变形为1.3 mm,相对于优化前机械臂末端变形减小了13.3%。优化前后机械臂动力学特性对比见表1。 从表1可以看出,优化前后机械臂前两阶固有频率均有所增大,分别提高了3.2%和3.9%,优化后的机械臂在额定负载下最大应力减小到5.5 MPa,末端总位移由1.5 mm减小到1.3 mm,表明机械臂总体刚度和强度性能指标均有所提高,优化后的机械臂动力学性能得到明显提高。 (a)总应力云图 (b)总变形云图图8 优化后机械臂总应力云图和总变形云图Fig.8 Total stress and deformation nephogram 性能指标优化前优化后相对变化量(%)一阶固有频率(Hz)21.622.303.2二阶固有频率(Hz)27.929.003.9最大应力(MPa)6.25.50-11.3最大变形(mm)1.51.30-13.3结构质量(kg)13.112.40-5.0载重/自重比0.30.326.3 本文结合“转子-扭簧”模型和有限元法建立了机械臂柔性多体动力学模型,通过对比分析不同部件的关节刚度变化对机械臂前五阶固有频率的影响规律可以发现:关节刚度的增大会使相应固有频率提高,腰关节刚度主要影响与腰部扭转有关的机械臂侧方向摆动固有频率,大臂关节主要影响机械臂末端上下振动频率,肘关节主要影响肘部弯曲振动频率,在对机械臂进行优化时必须考虑关节刚度的影响。 通过考虑关节柔性和臂杆柔性对机械臂进行拓扑优化,相对初始设计模型,优化后的机械臂前两阶固有频率和自身载重/自重比均有所提高,额定负载下的最大应力和末端总位移均有所减小,表明机械臂自身动力学性能得到提升。该研究结果可为机械臂本体的动力学优化和相关类型产品的改进升级提供理论依据。 [1] HEGDEE G S, VINOD M S, SHANKAR A. Optimum Dynamic Design of Flexible Robotic Manipulator[J]. International Journal of Mechanics and Materials in Design,2009,5(4):315-325. [2] 王斌锐, 方水光, 金英连. 综合关节和杆件柔性的机械臂刚柔耦合建模与仿真[J]. 农业机械学报,2012,43(2):211-215. WANG Binrui, FANG Shuiguang, JIN Yinglian. Dynamics and Simulation of Rigid-flexible Coupling Robot Arm with Flexible Joint and Link[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(2):211-215. [3] 刘燕, 刘洋. 基于变柔性关节的机械臂运动误差研究[J]. 机械设计,2010,27(12):62-65. LIU Yan, LIU Yang. Study onKinematics Error of Manlpulator Based on Variable Flexible Joint[J]. Journal of Machine Design,2010,27(12):62-65. [4] SPONG M W. Modeling and Control of Elastic Joint Robots[J]. Journal of Dynamic Systems, Measurement and Control,1987,109(1):310-319. [5] BAHRAMI M, RAHI A. Tip Dynamic Response of Elastic Joint Manipulators Subjected to a Stochastic Base Excitation[J]. JSME International Journal: Series C,2003,46(4):1502-1508. [6] 卢剑伟, 陈昊, 孙晓明, 等. 考虑减速机构间隙的机械臂动力学建模分析[J]. 机械工程学报,2013,49(15):15-21. LU Jianwei, CHEN Hao, SUN Xiaoming, et al. Dynamic Modeling and Analysis of Robot Arm with Consideration of Clearance in Gear Reducer[J]. Journal of Mechanical Engineering,2013,49(15):15-21. [7] Al-YAHMADI A S, ABDO J, HSIA T C. Modeling and Control of Two Manipulators Handling a Flexible Object[J]. Journal of the Franklin Institute,2007,344(5):349-361. [8] ZHANG H W, AHMAD S, LIU G J. Modeling of Torsional Compliance and Hysteresis Behaviors in Harmonic Drives[J]. IEEE /ASME Transactions on Mechatronics,2015,20(1):178-185. [9] GAO Dongming, WANG Dacheng, WANG Guanghui, et al. Topology Optimization of Conditioner Suspension for Mower Conditioner Considering Multiple Loads[J]. Mathematical and Computer Modelling,2013,58:489-496. StructureOptimizationDesignofRobotArmBasedonFlexibleMulti-bodyDynamics LIANG Mingxuan1,2,3LI Zhenggang2TANG Renzhong1CHEN Li2HUANG Chuan2 1.College of Mechanical Engineering, Zhejiang University, Hangzhou,310027 2.Hangzhou Siasun Robot Automation Co., Ltd., Hangzhou,310000 3.College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou,310018 Aiming at the influences of the flexible joints on the dynamics of industrial robots, the effect laws of the joint stiffness on the natural dynamics characteristics of the robot arm were investigated based on the rotor-torsional spring model and the finite element method. A flexible multi-body dynamics model of robot arm was established by considering the flexible characteristics of the arms and the joints. The topology optimization on the robot arms was carried out by taking the lightweight as the design goal and the total displacement as the constraints. The results indicate that the tare-load ratio of the optimized robot arm increases, the stiffness and strength of the robot arm enhances, and the overall dynamics performance improves significantly. robot arm; joint stiffness; flexible multi-body dynamics; topology optimization; tare-load ratio TK122 10.3969/j.issn.1004-132X.2017.21.008 2016-12-30 国家自然科学基金资助项目(51705494);浙江省自然科学基金资助项目(LQ17E050005) (编辑陈勇) 梁明轩,男,1986年生。浙江大学机械工程学院和杭州新松机器人自动化有限公司联合培养博士后研究人员,中国计量大学机电工程学院讲师。研究方向为机器人机电耦合系统动力学优化、转子非线性动力学及振动控制。发表论文7篇。E-mail:mingliangxuan@163.com。李正刚,男,1966年生。杭州新松机器人自动化有限公司总经理、高级工程师。唐任仲,男,1960年生。浙江大学机械工程学院教授、博士研究生导师。陈立,男,1984年生。杭州新松机器人自动有限公司研究院院长、高级工程师。黄川,男,1988年生。杭州新松机器人自动化有限公司工程师。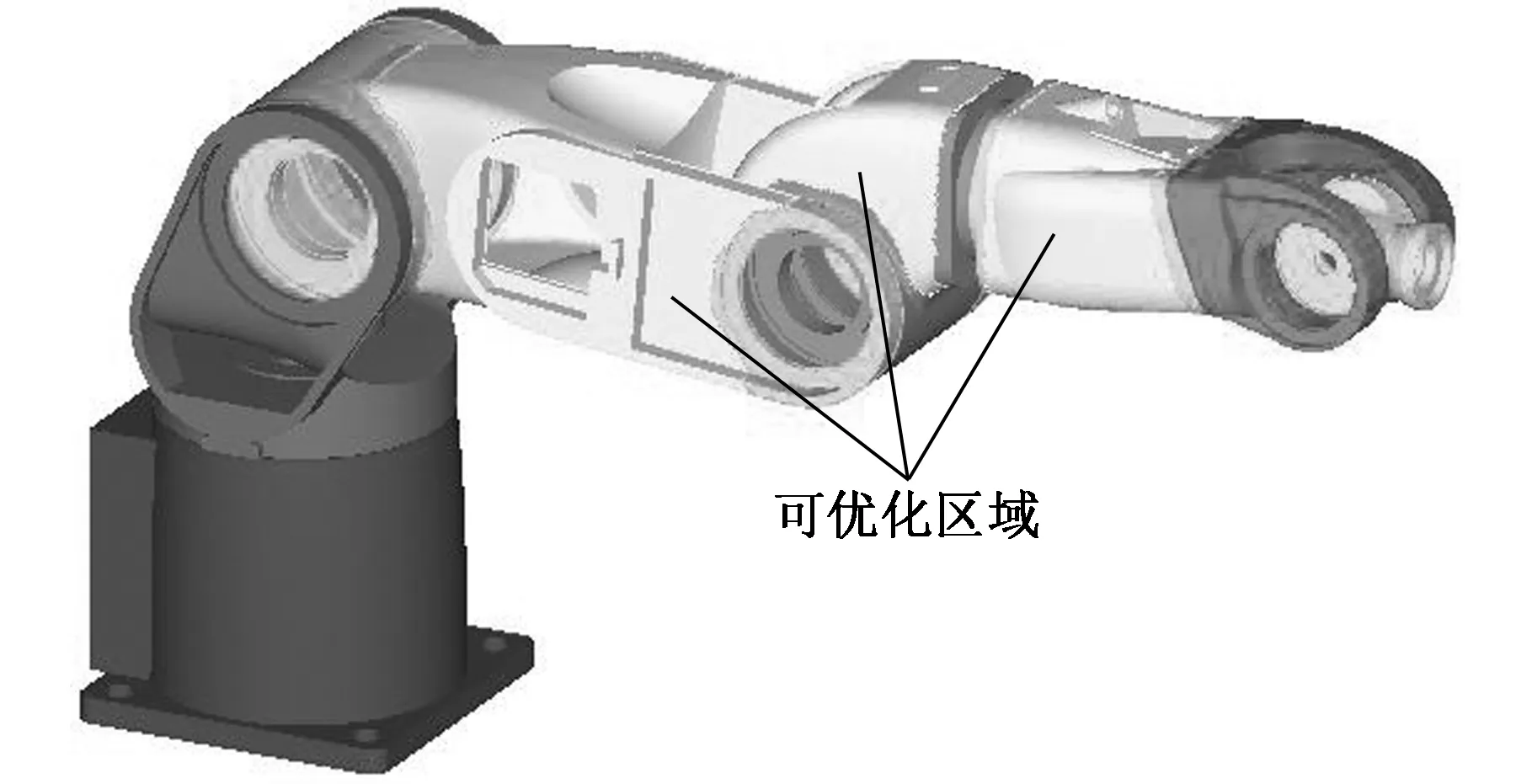






3 结语

