改进小生境蝙蝠算法在无功优化中的应用
罗荇子,汪 沨,谭阳红,胡君楷,王 睿
(湖南大学电气与信息工程学院,长沙 410082)
改进小生境蝙蝠算法在无功优化中的应用
罗荇子,汪 沨,谭阳红,胡君楷,王 睿
(湖南大学电气与信息工程学院,长沙 410082)
为了克服基本蝙蝠算法后期收敛速度慢、易陷入局部最优的缺点,在原始算法中引入小生境技术并进行改进。在改进算法中,将小生境半径设置为自适应变化的动态函数;在单个小生境群体中采用信息共享机制,对相似蝙蝠数量的过度增长进行抑制;采用优质蝙蝠邻域搜索及存储策略对每一代每个小生境群体的优质蝙蝠进行储存。对某21节点系统进行了无功优化,并与遗传算法、基本蝙蝠算法进行比较,结果表明改进的算法具有更好的全局搜索能力和收敛性能。
无功优化;小生境;蝙蝠算法;小生境半径动态划分;信息共享机制
紧跟着经济发展的脚步,中国电力行业也在不断进步中,日益扩大的电网规模和持续增长的负荷需求对系统的安全、稳定、经济运行提出了更高的要求。在此背景下,现代电力系统中无功功率的影响及其辅助服务日渐得到重视,如何有效利用系统的既有无功资源并合理配置无功补偿设备,以期达到降低网损、提高电压控制能力的目的,对电网的经济可靠运行以及提升电能供应质量等都有重要意义[1-5]。
电力系统无功优化即通过对系统中某些可控变量(如发电机端电压、无功补偿装置投入点及配置容量、变压器分接头、分布式电源接入等)进行调控,使系统在满足各项约束条件下达到目标运行状态的优化问题,其属于多变量、约束多样的混合非线性规划问题。传统的优化算法,如非线性规划法、内点法、混合整数规划法等,均被应用于无功优化当中,并表现出了一定的收敛性和适应性,但传统优化算法具有求解时间长、要求目标函数可微、因“维数灾”限制而难以对大规模优化问题进行求解等缺点。近年来,一些人工智能算法迅速发展并被引入电力系统的运算分析中,遗传算法GA(genetic algorithm)[6-7]、模拟退火算法[8]、粒子群算法[9-11]等均被应用于无功优化问题中。然而,在计算分析过程中,各种算法表现出了不同的缺点,如遗传算法易出现早熟收敛;模拟退火算法对退火方案的选择具有较高的敏感性,而优化方案的初值和优化参数均难以确定;禁忌搜索算法在进行单点搜索时获得的初始解对收敛速度和最终解的优劣度有很大影响;粒子群算法易陷入局部最优解。
蝙蝠算法 BA(bat algorithm)[12]是剑桥大学Yang教授于2010年提出的一种新型启发式算法,其基于仿生方法启发于蝙蝠回声定位的目标搜索行为方式,目前已被应用于工程优化问题中。该算法规则简单,参数设置简易,具有潜在并行性,随着微型蝙蝠(算子)的移动能自主调节全局大范围搜索与局部邻域搜索的比重。本文建立了无功优化模型,并将蝙蝠算法应用于区域配电网无功优化运算中,对算法中优化参数的更新公式进行改进,使微型蝙蝠能更优质地分布于搜索域,提高全局搜索能力。在此基础上,引入小生境技术,提出改进小生境蝙蝠算法INBA(improved niche bat algorithm),利用动态聚集方法划分小生境群体,在迭代过程中实现小生境内适应度信息共享,提高算法的收敛速度。通过算例仿真并与其他算法相比较,表明了算法的有效性。
1 无功优化数学模型
无功优化以发电机端电压、变比可调变压器分接头、无功补偿装置配置等为控制变量,通过改变上述变量来达到降低网损并保证电压稳定在规定范围内的目的。本文把有功网损最小作为优化算法的目标函数FΩ,即

式中:Pk,loss为系统有功网损;N为系统支路数;n为系统节点数;Gij为节点i、j间的支路电导;Ui、Uj分别为节点i、j电压;θij为节点i、j电压相角差。
考虑到优化过程中可能会出现系统节点和发电机无功功率越界情况,把上述目标函数拓展为带罚函数的形式,即
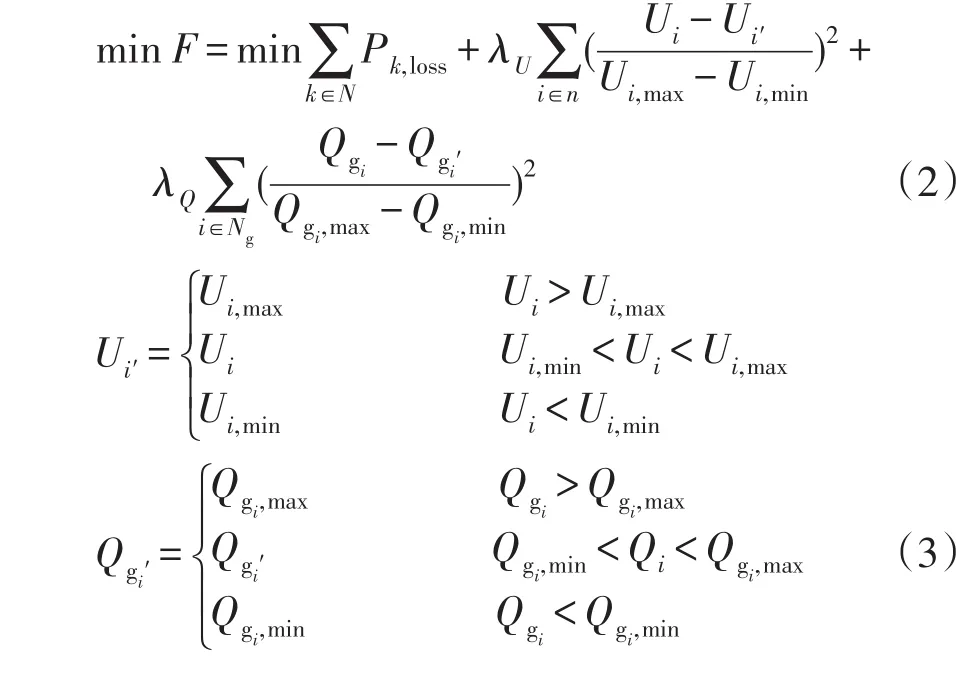
式中:λU、λQ为惩罚因数;Qgi为第i号发电机所发无功功率;Ng为发电机节点数;Ui,max、Ui,min分别为节点电压的上、下限值;Ui′、Qgi′为不同情况下节点电压和发电机无功出力的惩罚参数,其取值依据由式(3)给出;Qgi,max、Qgi,min分别为发电机可发无功的上、下限值。
目标函数式(2)还应附加约束条件,分别为潮流约束方程(等式约束)和变量约束条件(不等式约束),其公式为
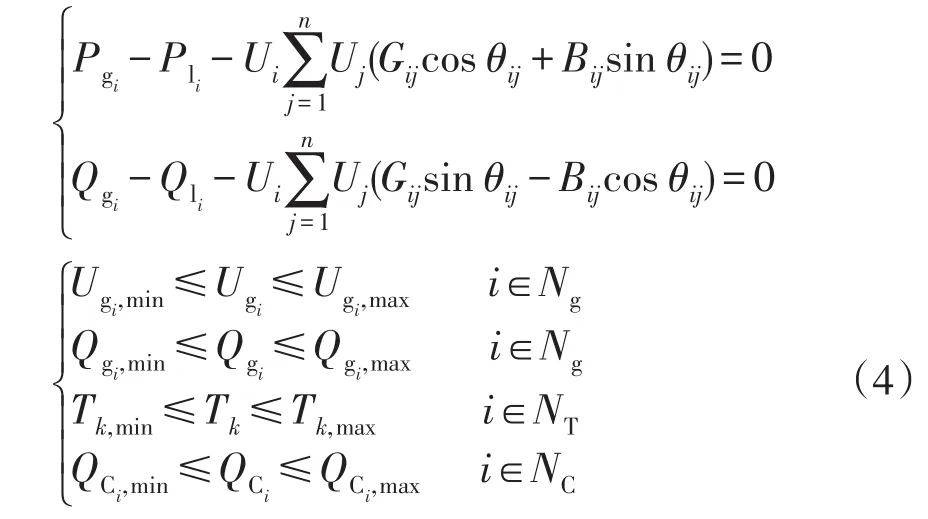
式中:Pgi、Qgi分别为发电机的有功功率和无功功率;Pli、Qli分别为节点i负荷的有功功率和无功功率;Bij为节点i、j间的电纳;优化运算过程中的控制变量Ugj、Tk、QCi分别为发电机端电压、可调变压器变比和无功补偿装置无功功率;NC和NT分别为投入无功补偿数和可调变压器节点数。
2 改进小生境蝙蝠算法
2.1 蝙蝠算法
蝙蝠算法的基本运算单元为微型蝙蝠,在搜索空间中蝙蝠所处某个位置时正对应一个优化问题的潜在解,微型蝙蝠本身固有的特征量有速度vi、发射脉冲的频率fi、发射脉冲的响度A。每个蝙蝠通过调整自身特征量以追随当前最优蝙蝠的趋势在空间中搜索,而当前处在最优位置的蝙蝠根据概率的动态变化进行局部搜索并判断是否接受新的更优解。基本蝙蝠算法的流程如下[13-14]。
步骤1初始化优化计算的目标函数和算法参数。设置蝙蝠种群大小nb、脉冲频率上限fu和下限fl、脉冲响度A0、脉冲发射率R,位置向量的维数D,最大迭代次数NI。
步骤2随机设置微型蝙蝠的初始位置及特征量。对单元蝙蝠i需随机产生1个脉冲频率fi和1个D维位置向量Xi0,并初始化1个D维零向量表示起始速度vi0且后续用于储存更新后的速度。
步骤3计算初始种群中各蝙蝠的适应度fitness,并检索出具有初代最优适应度值的蝙蝠X*。
步骤4对种群中各蝙蝠个体进行特征值更新运算,运算公式为

式中:t为当前迭代次数;β为随机变量系数,β∈[0,1];fu和fl分别为蝙蝠的脉冲频率上限和下限。
步骤5在每次迭代中,对于单元蝙蝠生成随机数rand1,若rand1>R(i)(R(i)为第i只蝙蝠的脉冲发射率),则选择当前最佳解对其进行局部扰动,判断是否接受扰动后的解为新解。判断依据为:计算扰动后蝙蝠的新适应度,若新适应度优于自身最优适应度或随机数rand2<A(i)(A(i)为第i只蝙蝠的脉冲响度),就用扰动后的新位置替换旧位置进行储存。
步骤6检索本次迭代过程中是否存在单元蝙蝠的适应度优于全局最优适应度,若存在,则对全局最优解的位置和适应度值进行更新。
步骤7更新响度和脉冲率,其更新公式为

式中,α和γ为预设量,0<α<1,γ>0。
步骤8判断结束条件是否满足,若不满足,跳转步骤4,若满足,跳转步骤9。
步骤9搜索停止,输出全局最优解对应单元蝙蝠的位置和适应度。
2.2 小生境技术
由前文对蝙蝠算法的描述可以发现,其对问题最优解的搜索是通过蝙蝠个体间的相互作用来完成的。因而当蝙蝠种群中出现超级蝙蝠(即区域暂时最优解)时,容易导致搜索目标陷入局部最优。在采用蝙蝠算法的基础上引入小生境技术[15],利用局部最优解和小生境群体间信息共享逐步搜索,从而确定最优解。
小生境技术是效仿特定环境生态平衡的一种仿生技术,其来源于生物进化过程中一般在某一特定的环境区域中与同物种在一起生存繁衍的现象。小生境技术在应用于智能算法时,将种群当作一个生态系统,在每一次迭代计算中将种群基本单元依照某种共性划分为多个小生境群体。在小生境内部,单元算子间具有一定的信息共享和淘汰机制;而在对于不同小生境群体,其分别形成相对独立的搜索空间,使多个具有邻域搜索价值的局部极值得以保留。
2.3 小生境蝙蝠算法的步骤与改进
小生境蝙蝠算法的基本思想是在单元蝙蝠进行目标搜索的过程中引入小生境技术,根据蝙蝠个体间的相似程度划分一系列小生境蝙蝠群体。在各个小生境群体中构建信息共享机制,筛选出局部最优蝙蝠和劣质蝙蝠,随后对劣质蝙蝠的适应度进行调整继而在小生境中淘汰。将被淘汰劣质蝙蝠的特征值初始化,使其重新在搜索区域中搜索目标。本文针对小生境蝙蝠算法提出了一系列改进措施,措施的关键点如下。
1)小生境半径的动态取值
小生境半径是划分小生境群体的重要依据,在原始算法中小生境半径多被设为恒定常数,该做法虽简易便于实现,但却具有较大弊端:小生境半径过小时,由初始种群划分出的小生境群体数量过多,造成数据冗余;小生境半径过大时,初始种群无法被划分为相对独立的小生境群体,小生境技术的作用效果不明显。本文对小生境半径L0的设定采用动态取值的方法进行改进。在优化运算的全过程中,每一代小生境半径由当前种群内蝙蝠两两间的欧式距离决定,因而小生境半径在每一代运算中的适应性得到保证,使划分小生境种群的数量至少为2,并且种群规模更为合理。
初始种群包含m只蝙蝠,第i只蝙蝠的位置Xi=[xi1,xi2,…,xid],该蝙蝠与第j只蝙蝠间的欧式距离记为dij=||Xi-Xj||,L在运算之始被赋予一常数初值,随着运算的进行,每一代小生境半径L(t)的更新公式为
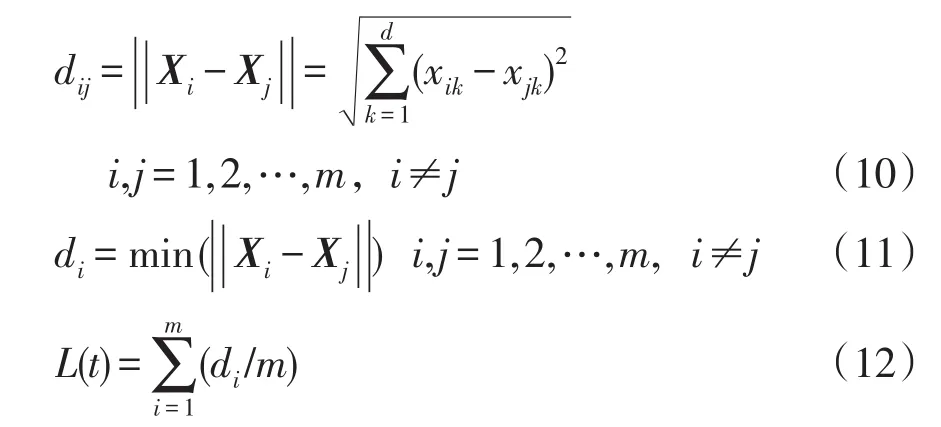
在某一代运算中,若某两只蝙蝠间的欧式距离di,j<L(t),则这两只蝙蝠被划归至同一小生境群体中。
2)信息共享机制
共享函数确定了单元蝙蝠在小生境群体中的共享度,并作为小生境群体内蝙蝠调整个体适应度的依据。
中韩两国教育技术学专业对本科阶段的素质和能力方面的要求有许多相同之处。在素养方面都有以下要求:①文化素质。包括文化素养、文学艺术修养、人际交往意识;②专业素质。包括科学的思维方法、研究方法,具备创新意识和严谨的科学素养;③身心素质。包括具有较好的身体和心理素质。中韩两国对能力的要求也都大致分为以下4个方面:教学设计能力、影视与多媒体方面的创作能力、教育软件的设计和开发能力、数字化教学环境的建设能力。
共享函数和调整后的适应度分别为

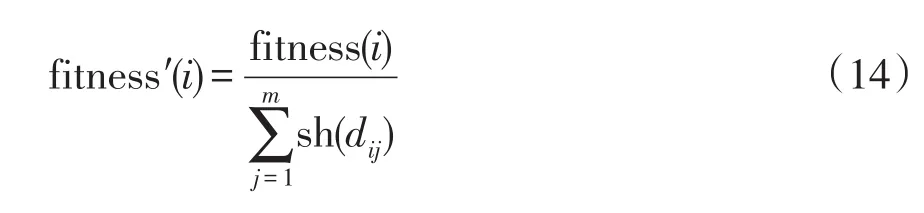
式中:sh(dij)为共享函数;fitness(i)和fitness′(i)分别为第i只蝙蝠的初始适应度和调整后的适应度。
可以看出,一个小生境群体内两个蝙蝠之间的相似度越高,共享函数值越大;小生境群体内个体数越多,共享函数值越大,则对于某只单元蝙蝠来说,其个体适应度的降幅越大。由于信息共享机制的作用,小生境群体中相似蝙蝠数量不至于过度增长,种群的多样性得到保持,控制了局部收敛现象和早熟现象的出现。
3)优质蝙蝠邻域搜索及存储策略
在每一代计算中,不仅保留适应度全局最优的蝙蝠作为最优个体,还对每一个小生境群体内部进行局部最优蝙蝠的筛选,并将局部最优蝙蝠存储保留到下一代计算。在下一代计算中,对局部最优蝙蝠的邻域也进行目标搜索。该策略容许多个优质蝙蝠的存在,并对多个潜在最优蝙蝠进行邻域搜索,能最大程度保证真正最优个体不被遗漏。INBA进行无功优化问题求解流程如图1所示。
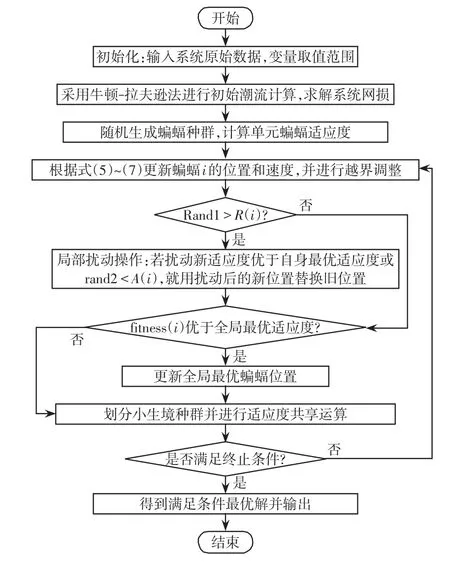
图1 INBA无功优化求解流程Fig.1 Flow chart of solving reactive power optimization based on INBA
3 模型求解
采用处理器2.53 GHz,内存为4 GB的PC在MATLAB R2010b环境下对某21节点系统进行无功优化计算,系统线路基本参数保持不变[16],其中节点17、21接入光伏发电分布式电源,网络结构图如图2所示,并假设在节点6配置无功补偿电容器,系统可控变量为1节点电压、可调变压器变比和电容器补偿无功。
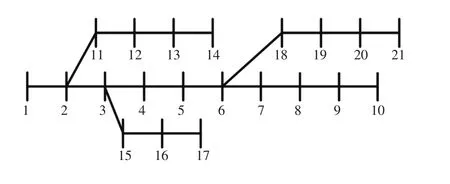
图2 21节点系统Fig.2 21-node system
系统三相功率基准值为10 MW,基准电压为10 kV,节点1为平衡节点,负荷节点电压限值为[0.95,1.05]。改进小生境蝙蝠算法参数设置如下:蝙蝠种群大小nb=36,最大迭代次数NI=500,蝙蝠脉冲频率上限fu=1、下限fl=0,初始脉冲发射速率R0=0.75,初始响度A0=0.25。分别采用遗传算法、基本蝙蝠算法、改进小生境蝙蝠算法对该系统进行无功优化计算,并对3种算法性能进行比较分析。
经过优化分析,优化结果如表1、图3所示。

表1 不同算法的优化结果Tab.1 Optimization results by using different methods
由图3可知,仿真模型中设置的罚函数可对出现越限情况的状态变量进行罚除,遗传算法和改进小生境蝙蝠优化结果均未出现节点电压越限,蝙蝠算法优化结果中有两个节点电压偏低。由数据结果可得,优化前系统节点电压偏离度为0.561 8,遗传算法优化的节点电压偏离度为0.720 9,蝙蝠算法优化及改进小生境遗传算法优化后,节点电压偏离度分别0.562 2和0.238 9,改进小生境遗传算法优化结果的电压质量更高。
图4为采用3种优化算法对算例进行无功优化的网损收敛曲线。由图可以看出,遗传算法收敛速度最快,但在优化过程中出现了早熟收敛现象;蝙蝠算法表现出了较好的寻优性能,但在运算后期收敛速度慢;改进小生境遗传算法并未陷入局部最优解,表现出了更好的全局寻优能力和收敛能力。

图3 优化前后节点电压Fig.3 Nodal voltages before and after optimization
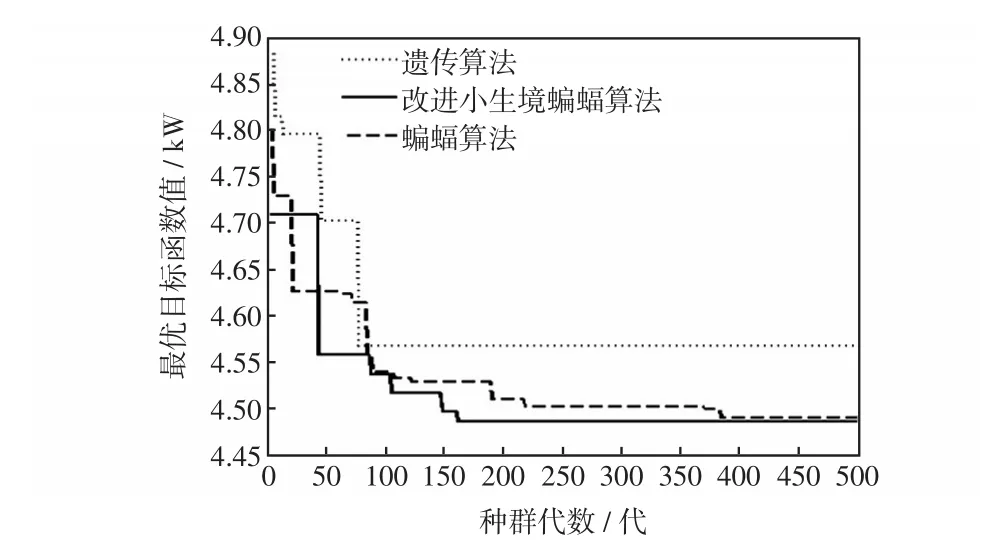
图4 3种优化算法的网损收敛曲线Fig.4 Network loss convergence curves based on three optimization algorithms
4 结 语
本文在进行无功优化时以系统的有功网损最小化作为优化目标,在数学模型中对节点电压越界和发电机无功出力越界的情况采用罚函数方式进行处理。将小生境技术引入蝙蝠算法并进行改进:以自适应调节的小生境半径为依据划分小生境群体,使每代划分出小生境群体的数量和规模更为合理;在小生境群体内采用信息共享机制对相似蝙蝠的适应度进行调整,通过调整劣质蝙蝠个体的适应度来限制个别个体对其他个体的误导作用,改善了算法的全局搜索能力和收敛性能。将改进后的算法用于电力系统的无功优化,仿真实验表明,该算法能显著降低系统的有功网损,且获得的最优解质量较高,对解决实际电力系统的无功优化问题具有一定的实用价值。
[1]张勇军,任震,李邦峰(Zhang Yongjun,Ren Zhen,Li Bangfeng).电力系统无功优化调度研究综述(Survey on optimal reactive power dispatch of power systems)[J].电网技术(Power System Technology),2005,29(2):50-56.
[2]陈树勇,宋书芳,李兰欣,等(Chen Shuyong,Song Shufang,Li Lanxin,et al).智能电网技术综述(Survey on smart grid technology)[J].电网技术(Power System Technology),2009,33(8):1-7.
[3]朱兰,严正,杨秀,等(Zhu Lan,Yan Zheng,Yang Xiu,et al).计及需求侧响应的微网综合资源规划方法(Integrated resources planning in microgrid based on modeling demand response)[J].中国电机工程学报(Proceedings of the CSEE),2014,34(16):2621-2628.
[4]张志强,苗友忠,李笑蓉,等(Zhang Zhiqiang,Miao Youzhong,Li Xiaorong,et al).电力系统无功补偿点的确定及其容量优化(Location selection of reactive power compensation and compensation capacity optimization)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2015,27(3):92-97.
[5]程振龙,唐晓骏,任惠,等(Cheng Zhenlong,Tang Xiaojun,Ren Hui,et al).考虑电压稳定约束的无功补偿优化配置(Optimal configuration of reactive power compensation considering voltage stability constraints)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2015,27(4):86-91.
[6]李惠玲,盛万兴,张学仁,等(Li Huiling,Sheng Wanxing,Zhang Xueren,et al).改进小生境遗传算法在电力系统无功优化中的应用(Application of improved niche genetic algorithm in reactive power optimization)[J].电网技术(Power System Technology),2008,32(17):29-34.
[7]刘方,颜伟,David C Yu(Liu Fang,Yan Wei,David C Yu).基于遗传算法和内点法的无功优化混合策略(A hybrid strategy based on GA and IPM for optimal reactive power flow)[J].中国电机工程学报(Proceedings of the CSEE),2005,25(15):67-72.
[8]陈皓勇,王锡凡(Chen Haoyong,Wang Xifan).电力系统无功优化的退火选择遗传算法(A genetic algorithm with annealing selection for reactive power optimization)[J].中国电力(Electric Power),1998,31(2):3-6.
[9]Zhao B,Guo C X,Cao Y J.A multiagent-based particle swarm optimization approach for optimal reactive power dispatch[J].IEEE Trans on Power Systems,2005,20(2):1070-1078.
[10]任新伟,徐建政(Ren Xinwei,Xu Jianzheng).改进细菌群体趋药性算法在无功优化中的应用(Application of improved bacterial colony chemotaxis algorithm in reactive power optimization)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2015,27(5):81-85.
[11]刘自发,张建华(Liu Zifa,Zhang Jianhua).基于自适应小生境粒子群优化算法的电力系统无功优化(Reactive power optimization based on adaptive niche particle swarm optimization algorithm)[J].电力自动化设备(Electric Power Automation Equipment),2009,29(11):27-30.
[12]Yang X S.A new metaheuristic bat-inspired algorithm[J].Nature Inspired Cooperative Strategies for Optimization,SCI 284,2010:65-74.
[13]刘长平,叶春明(Liu Changping,Ye Chunming).具有混沌搜索策略的蝙蝠优化算法及性能仿真(Bat algorithm with chaotic search strategy and analysis of its property)[J].系统仿真学报(Journal of System Simulation),2013,25(6):1183-1188,1195.
[14]刘云连,伍铁斌,王俊年,等(Liu Yunlian,Wu Tiebin,Wang Junnian,et al).改进罚函数法与蝙蝠算法在约束优化中的应用(Application of modified penalty function method and bats algorithm in constrained optimization)[J].计算机工程与应用(Computer Engineering and Applications),2015,51(9):62-67.
[15]崔挺,孙元章,徐箭,等(Cui Ting,Sun Yuanzhang,Xu Jian,et al).基于改进小生境遗传算法的电力系统无功优化(Reactive power optimization of power system based on improved niche genetic algorithm)[J].中国电机工程学报(Proceedings of the CSEE),2011,31(19):43-50.
[16]胡晨成,于艾清,柏扬,等(Hu Chencheng,Yu Aiqing,Bai Yang,et al).基于GA的电力系统多目标模糊无功优化(Multi-objective fuzzy reactive power optimization based on GA)[J].上海电力学院学报(Journal of Shanghai University of Electric Power),2014,30(6):525-529.
Application of Improved Niche Bat Algorithm to Reactive Power Optimization
LUO Xingzi,WANG Feng,TAN Yanghong,HU Junkai,WANG Rui
(School of Electrical and Information Engineering,Hunan University,Changsha 410082,China)
In order to overcome the shortcomings of bat algorithm(BA)such as low convergence speed in the later period of optimization and vulnerability to falling into local optimums,niche technique is introduced to improve the original BA.The improvements are as follows:niche radius is set as a dynamic function,which varies adaptively;information sharing mechanism is adopted in a single niche community to restrict the excessive growth of similar bats;the strategies of neighborhood search and storage with valued bats are used to preserve the potential optimal bats in each generation of each community.The reactive power optimization of a 21-node system is carried out,whose result is compared with those obtained by using genetic algorithm(GA)and BA,indicating that the improved algorithm has better global search and convergence performance.
reactive power optimization;niche;bat algorithm(BA);dynamic partitioning of niche radius;information sharing mechanism
TM71
A
1003-8930(2017)10-0035-05
10.3969/j.issn.1003-8930.2017.10.007
2016-01-12;
2017-06-28
国家自然科学基金资助项目(61102039);湖南省自然科学基金资助项目(14JJ7029);中央高校基金资助项目;湖南省教改课题资助项目
罗荇子(1992—),女,硕士研究生,研究方向为电力系统分析及电力系统过电压。Email:luoxingzi2010@163.com
汪 沨(1972—),男,博士,教授,博士生导师,研究方向为高电压绝缘及气体放电及电力系统分析。Email:wangfeng55@263.com
谭阳红(1971—),女,教授,博士生导师,研究方向为配电网故障诊断、智能与实时信息处理。Email:tanyho@126.com
——以贵阳花溪公园为例

