LCL型并网逆变器的GCFAD优化设计方法

汪 英，周乐明

（1.湖南邮电职业技术学院，长沙 410015；

2.湖南大学国家电能变换与控制工程技术研究中心，长沙 410082）

LCL型并网逆变器的GCFAD优化设计方法

汪 英1，周乐明2

（1.湖南邮电职业技术学院，长沙 410015；

2.湖南大学国家电能变换与控制工程技术研究中心，长沙 410082）

针对并网电流反馈有源阻尼（GCFAD）方法在谐振尖峰抑制程度与响应速度上存在着两个相互制约的参数且不利于提高LCL型并网逆变器动态性能的问题，推导了GCFAD的等效虚拟阻抗模型，阐述了系统动态性能指标与GCFAD参数的本质关系。并在结合零极点模型和劳斯稳定判定的基础上，提出了一种改善LCL型并网逆变器动态性能的GCFAD优化设计方法。将GCFAD的两变量降为单一变量控制，降低了参数设计复杂程度，解除了两制约参数的耦合关系，使控制系统具备最佳的动态性能。仿真与实验结果表明：LCL并网逆变器的满载并网电流畸变率仅为2.2%；当系统从半载跳变到满载时，系统超调量仅为8%，相较于其他设计方法具有更快的响应速度与更小的超调量。

并网逆变器；LCL滤波器；有源阻尼；数字高通滤波器；动态性能

化石能源的短缺及造成的环境污染使得新能源分布式发电成为研究热点之一，并网逆变器是连接分布式系统与公共电网的关键装置，在分布式发电系统中起着至关重要的作用[1-2]。然而逆变器脉宽调制产生的高次谐波危及并网系统的安全及稳定运行，必须进行必要的抑制或滤除。LCL型并网逆变器因其优越的高频谐波抑制能力及低总电感量，受到人们广泛重视，但LCL滤波器是三阶系统，存在谐振问题，容易发生振荡并造成系统不稳定，因此对系统控制策略提出了更高的要求[3-5]。

LCL滤波器谐振尖峰抑制方法分为无源阻尼和有源阻尼两种[6]。有源阻尼通过增加额外的反馈控制，获得与无源阻尼同样的谐振尖峰抑制效果，实现方式灵活可调，且不会带来额外的功耗，成为近年研究与应用的热点。文献[7-8]均是采样LCL滤波器中的电容电流并进行反馈控制，增加系统阻尼，实现简单方便，但由于高频电容电流幅值较小，增加了精确处理控制变量数据的难度。文献[9]提出采用网侧电感电压微分量反馈实现谐振尖峰的抑制，文献[10-12]提出通过反馈电容电压微分量增加系统阻尼，然而微分环节在实际工程中难以实现，增加了设计难度。以上文献对并网电流闭环控制除了所需的并网电流传感器，均还需增加额外的电流或电压传感器，增加了系统硬件成本，且不利于系统可靠性。文献[13]提出一种采用并网电流两次微分的反馈方法，实现谐振阻尼控制，无需增加额外传感器，但导函数将会带入噪声放大，造成系统振荡，且反馈参数也不易选取。文献[14]估算并反馈当前电容电流值，虽未引入额外的传感器，但电容电流的估算方法较为复杂耗时，且容易引入误差。文献[15-18]探讨对LCL逆变器谐振尖峰附近的输出频率反馈控制，并提出并网电流反馈有源阻尼GCFAD（grid current feedback active damping）方法来抑制谐振峰值，该方法无需额外的传感器，却很好地增加了系统阻尼系数，减少了系统硬件成本，提高了系统可靠性，在工程中采用数字高通滤波器也易于实现，但该策略存在两个相互制约参数，影响系统响应速度与阻尼程度，难以获得系统最佳动态性能。文献[17-18]虽然给出了并网电流反馈有源阻尼方法的初步设计方案，却未从本质上阐述该方法抑制谐振尖峰的机理，且该策略如何合理选择参数成了一个亟待解决的难点问题。

综上所述，本文首先推导了GCFAD的等效虚拟阻抗模型，深入分析其抑制谐振尖峰的机理，阐述系统动态性能指标与该方法参数的本质联系。然后，基于系统动态性能与劳斯稳定判定，结合系统零极点模型，提出了一种提高LCL型并网逆变器动态性能的GCFAD优化设计方法，其给出参数优化设计方法，解决该方法中参数不易选取的难点，降低系统参数设计难度，提高系统动态性能。

1 LCL型并网逆变器系统模型

图1为LCL型单相并网逆变器结构，主要由直流稳压电源Udc、单相全桥逆变电路、LCL滤波器及电网构成。其中直流稳压电源通过储能电容Cdc和逆变器的直流侧相连，逆变器的交流侧接LCL输出滤波器，并与电网连接。电感L1、电容C以及电感L2构成LCL滤波器，R1和R2分别为滤波电感L1和L2的寄生参数；uinv为逆变器输出电压，ug和ig分别为电网电压和并网电流；uinv和iL分别为逆变器输出电压和电流；uC为滤波电容电压；K1为并网开关。

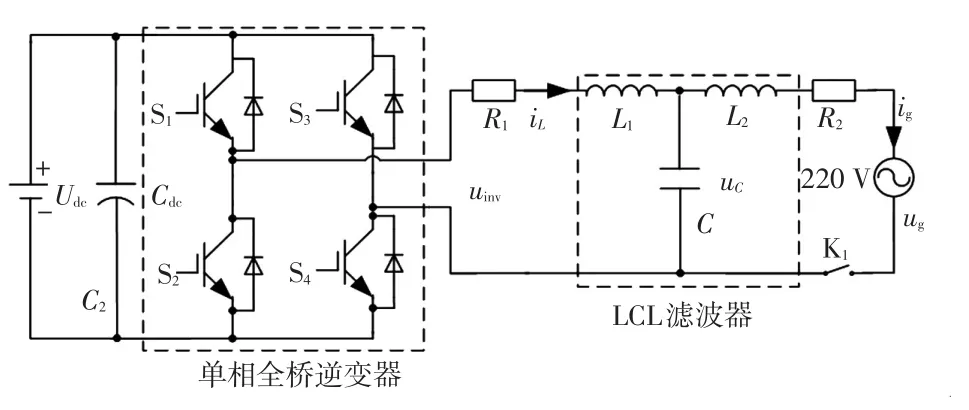
图1 LCL型单相并网逆变器结构Fig.1 Structure of LCL-type single-phase grid-connected inverter

选取逆变器侧电流iL、并网电流ig以及滤波电容电压uC为状态变量，可得此逆变器系统的状态空间方程为

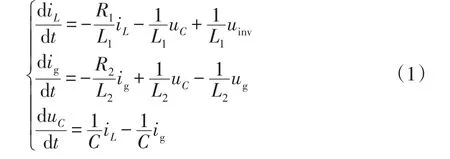
由式（1）可以得到LCL型逆变器系统的模型框图，如图2所示。

图2 LCL型逆变器系统的模型框图Fig.2 Block diagram of LCL-type inverter system

若将电网电压ug作为扰动信号，可推导出逆变器输出电压uinv到并网电流ig的传递函数[9-15]为

式中，R1、R2的阻值极小，可以忽略不计。由式（2）可知，传递函数Gd（s）在虚轴上存在一对共轭极点，将导致LCL型逆变器发生谐振，其谐振角频率ωres为

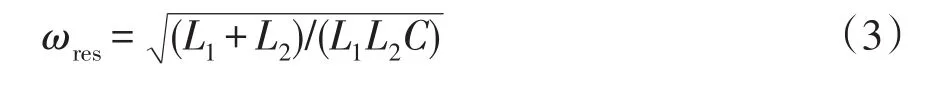
若不采用相应有效的阻尼方案抑制LCL型并网逆变器的谐振尖峰，系统将会发生振荡甚至造成系统不稳定。

2 GCFAD控制策略及参数设计分析

图3为单相LCL型逆变器并网电流反馈控制框图，主要包括电流外环和GCFAD环，电流外环实时调节并网电流，实现能量馈入电网；GCFAD环通过反馈并网电流的高频分量实现系统阻尼的增加，仅需对并网电流进行采样，无需额外的传感器，降低了硬件成本并提高了系统可靠性。其中，Gi（s）为电流调节器，iref为并网指令电流，ud为逆变器调制信号，Kinv为逆变器的等效增益。

图3 单相LCL型逆变器并网电流反馈控制框图Fig.3 Control block diagram of single-phase grid-current-feedback for LCL-type inverter

GCFAD的传递函数H（s）可表示为

式中，Kd、ωd分别为数字高通滤波器的增益和截止角频率。

2.1 等效虚拟阻抗模型

为了深入分析GCFAD抑制谐振尖峰的机理，阐述系统动态性能指标与该方法参数的本质联系。将图3中H（s）的反馈量前移至1/（sC）的输出端，将反馈点后移至1/（sL1）的输出端，得到的等效虚拟阻抗控制电路如图4（a）所示。其等效为在滤波电容并联上一个阻抗Zeq1，表达式为

Zeq1可表示为电阻R0和电容C0相并联，如图4（b）所示。将s=jω代入式（5），得到电阻R0和电容C0分别为

将虚拟电容C0与滤波电容C合并，根据式（6），推导出LCL滤波器的阻尼系数ξ0和实际谐振频率ωn分别为

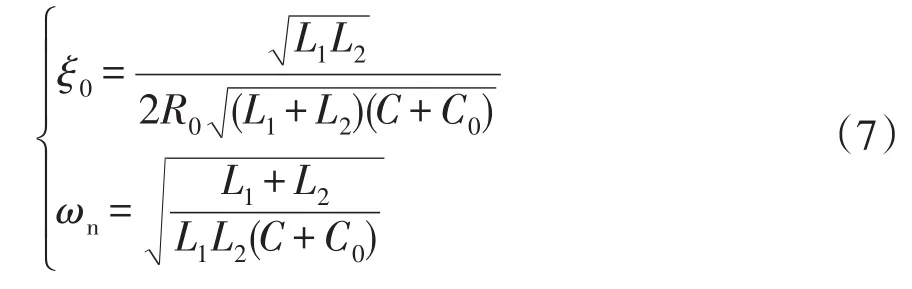
根据式（6）和式（7）可得，GCFAD不仅有效地增加了系统阻尼，能够较好地抑制谐振频率处的谐振尖峰，而且通过一阶数字高通滤波对低频区增益的抑制作用削弱有源阻尼反馈对较低频率处稳定性的影响；但等效在滤波电容的虚拟电容降低了系统谐振频率，影响了系统动态响应速度。同时虚拟电阻R0与虚拟电容C0的取值均由Kd、ωd共同决定，如何合理选择参数Kd、ωd需进行深入研究。

图4 GCFAD的等效并联阻抗Fig.4 Equivalent shunt impedance of GCFAD method

2.2 GCFAD设计难点

GCFAD的参数设计应满足系统稳定且具有良好的动态性能。系统动态性能主要指标为阻尼系数和动态响应速度，为了系统获得最佳动态性能，要求Kd和ωd有最优值使得系统具备较大的阻尼系数和较快的响应速度。

联立式（7），系统峰值时间tp和调节时间ts可表示为

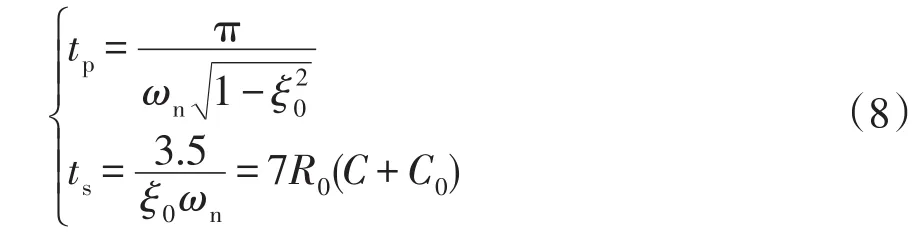
假设Kd恒定，ωd由大到小变化，由式（5）可知，等效电阻R0逐渐变小，等效电容C0也逐渐变小，联立式（6）和式（7），推导出系统峰值时间tp及调节时间ts均变小，阻尼系数ξ0变大，此时系统响应速度加快，阻尼系数增加；假设ωd恒定，Kd由小到大变化，同理可得系统峰值时间tp变大，调节时间ts变小，阻尼系数ξ0变大，此时系统阻尼系数增加，但响应速度降低。具体如表1所示。

表1 Kd、ωd变化时，系统性能参数变化情况Tab.1 Variation of system parameters with the changes of Kdand ωd

综上所述，增大Kd或减少ωd可增加系统阻尼，提高对LCL滤波器谐振尖峰的抑制能力；减少Kd或ωd可使系统峰值时间tp变小，提高系统动态响应速度。若仅考虑参数ωd，其值越小系统动态性能越好。

另一方面分析系统的稳定性，推导出Kd和ωd的取值范围。引入GCFAD后，并忽略滤波器的寄生电阻，逆变器调制信号ud到并网电流ig的传递函数Gd1（s）为

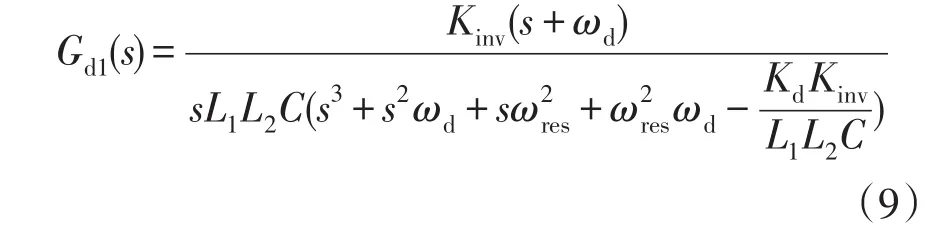
列写该传递函数的特征根方程为

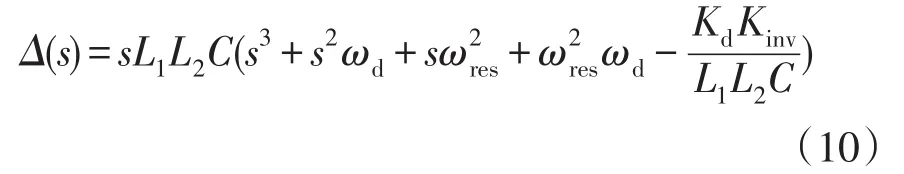
根据劳斯稳定判定依据，系统处于稳定状态时，Kd和ωd的应满足

由式（11）及上述系统动态性能分析结果可知，Kd和ωd相互制约，如Kd取值越大，系统阻尼系数增大，但相应地ωd极小值也变大，系统阻尼系数减少，响应速度降低，不利于系统动态性能。由此可知Kd和ωd基于劳斯稳定判定依据在动态性能和谐振抑制效果上相互影响，二者如何最优取值成为一个亟待解决的难点问题。

3 GCFAD优化设计方法

3.1 参数优化设计方法

由第2.2节可知，当Kd不变时，ωd取极小值，系统响应速度与谐振抑制能力达到最佳，但ωd的极小值却因系统稳定性与Kd存在着内部联系，需要更加深入地分析ωd的限制条件。而工程上常采用零极点对系统参数取值进行分析，本文需建立零极点模型阐述参数之间联系。

式（9）中，传递函数Gd1（s）存在3个非零极点和1个零点，除了原有的共轭复数极点外，并网电流有源阻尼策略引入了一个额外的实数极点和实数零点。由于额外引入的实数极点和零点不相等，不能相互抵消，因此，引入反馈后的传递函数特性与未引入反馈的二阶系统特性并不完全相同（暂不考虑零极点）。其中特征方程等效为

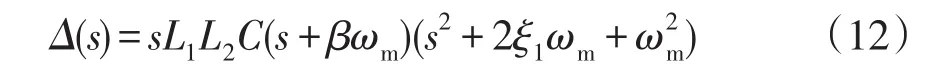
式中：ξ1为二阶系统中的阻尼系数；ωm为二阶系统中引入反馈后的谐振频率；β为引入的极点到虚轴的距离与共轭复数极点到虚轴距离的比例系数。

联立式（9）和式（12）可知，参数Kd、ωd和系统性能指标均由参数（ξ1、ωm、β）决定，并根据同次幂的系数相同可得

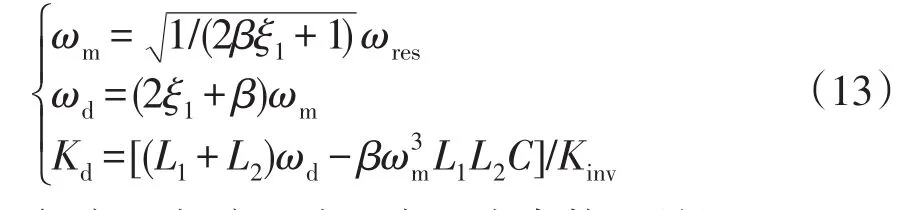
假定ωm恒定不变，则βξ1为常数，可得

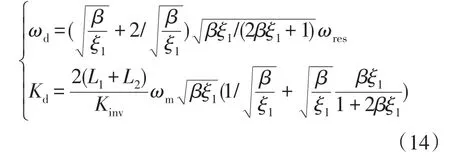
式中：当β=2ξ1时，ωd有极小值；当β=kξ1时，Kd有极小值。其中k为

显然k＞2，且在区间（0，2），Kd随着β/ξ1减少而增大。β/ξ1与有源阻尼参数的关系如表2所示。

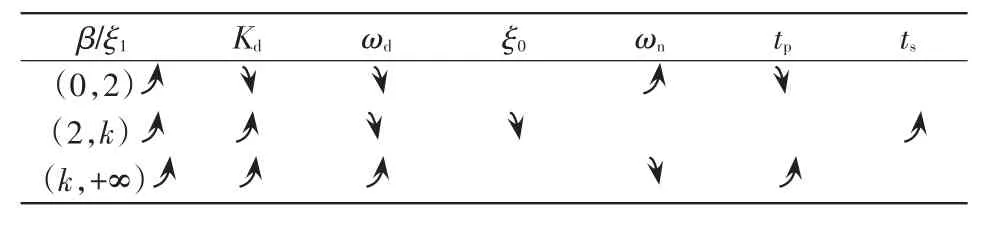
表2 β/ξ1变化时，系统性能参数变化情况Tab.2 Variation of system parameters with the change of β/ξ1

图5为ωm=1.55×104rad/s，β/ξ1分别取0.2、0.5、2、4、10时，传递函数Gd1（s）的波特图。显然GCFAD对谐振尖峰有较好的抑制效果，但随着β/ξ1的取值不同，系统稳定裕度与动态性能不同。此处传递函数Gd1（s）的截止频率（幅频曲线位于0 dB的频率）要低于穿越频率（相频曲线穿过±180°的频率），系统才会处于稳定。

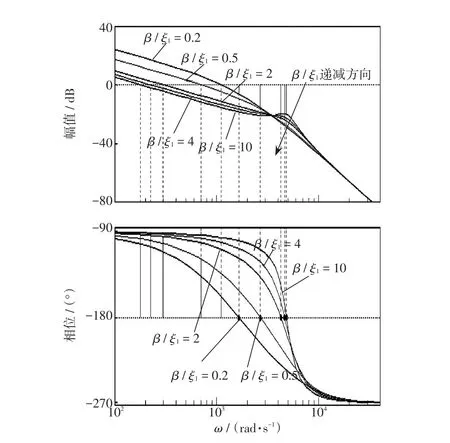
图5 β/ξ1不同比值时传递函数Gd1（s）的波特图Fig.5 Bode diagram of Gd1（s）at different ratios of β/ξ1

根据表2和图5可知，β/ξ1的取值可分成3部分来分析系统性能。①当β＜2ξ1，谐振尖峰得到很好的抑制（如图5），且随着β与ξ1的比值递增，ωd与Kd变小，系统峰值时间变小，系统动态性能变好，同时系统的稳定性能逐渐变好，相角裕度显著变大。如图5所示，K1=0.2ξ1时，穿越频率低于截止频率，系统不稳定；K1=0.5ξ1时，穿越频率高于截止频率，系统稳定。②当 2ξ1＜β＜kξ1，随着β/ξ1的比值增大，ξ0变小，系统阻尼减少，谐振尖峰效果变差，同时反映响应速度和阻尼程度的综合指标ts增大，系统动态性能变差。③当β＞2ξ1，随着β与ξ1的比值递增，ωd与Kd变大，系统峰值时间增大，系统动态性能变差。综上所述，仅β=2ξ1时，ωd有极小值使得系统的稳定性、响应速度以及谐振尖峰的抑制效果有最优值。

根据上述分析，并将β=2ξ1代入式（14），可得

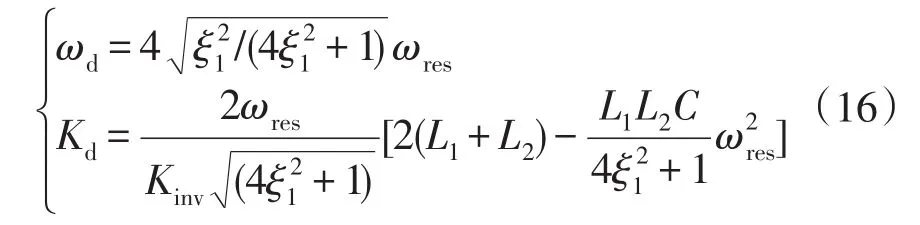
式（16）可知，GCFAD的两变量降为单一变量，ωd、Kd的取值仅由ξ1决定。调节ξ1就可获得系统最佳工作状态，不仅提高了系统的动态性能，而且降低了参数设计的难度。

同时将β=2ξ1和式（16）代入式（14），推导出系统稳定运行条件为

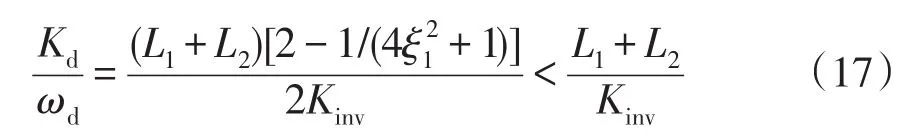
即

由式（18）可知，当β=2ξ1，无论ξ1取何值，系统都处于稳定状态。

3.2 参数 ξ1设计

根据第3.1节分析，传递函数Gd1（s）的相关性能参数表达式为

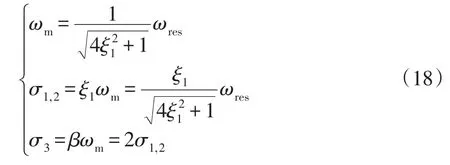
式中：σ1，2为共轭极点λ1、λ2到虚轴的距离；σ3为实数极点λ3到虚轴的距离。

由于

可得随着ξ1增大，σ1，2、σ3同时增大，系统调节时间变小。将式（16）代入式（9），暂不考虑零极点，单位阶跃响应下系统的调节时间ts、上升时间tr、超调量σ（%）及ωm/ωres的比值变化如图6所示。图6（a）为tr随着ξ1的增大而增大；图6（b）为σ（%）较小时，先随着ξ1增大而缓慢增大后快速变小；图6（c）为ts随着ξ1增大先快速变小，后趋于平稳，同时ts是反映响应速度和阻尼程度的综合指标，故为了获得系统最佳工作状态，则要求ξ1≥ξa（ξa为ts趋于稳定的最小值）；图6（d）为ωm/ωres随着ξ1增大不断减少，将会影响低频处稳定性，则要求ξ1不宜过大。

图6 单位阶跃响应下系统性能（不考虑零极点）Fig.6 System performance with unit step response（without the consideration of zero-pole）

取ξ1=0.3～0.7，ωm/ωres的比值为0.58～0.86，系统超调量适度，调节时间较短，对LCL谐振尖峰有很好的抑制效果，系统具有较快的动态性能。

本文给出了GCFAD的优化设计方案。当不计寄生电阻对有源阻尼优化方法影响，ωd与Kd具有一定的取值范围，可以在满足系统稳定性前提下，提高系统动态性能，对反馈参数进一步优化设计：①先假定ωm为常数，从稳定裕度、谐振抑制能力及动态响应速度的角度分析，推导出当β=2ξ1时，ωd有极小值使得系统性能最佳；②基于等式β=2ξ1的基础上，有源阻尼参数Kd、ωd仅由参数ξ1表示，降低了参数设计难度；③调节ξ1的取值，使得系统具有较好的稳定性能和较快的响应速度，工作于最佳状态。

4 仿真与实验

用MATLAB/Simulink建立了系统仿真模型，具体参数如表3所示。采用准谐振PR调节器对并网电流进行控制[19]，实现并网电流零稳态控制，其传递函数为

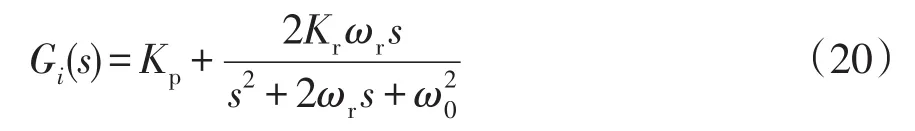
式中：ω0为基波角频率；Kp和Kr分别为准谐振PR控制器的比例系数和谐振增益；ωr为截止频率，可提高对电网频率轻微波动的适应性。

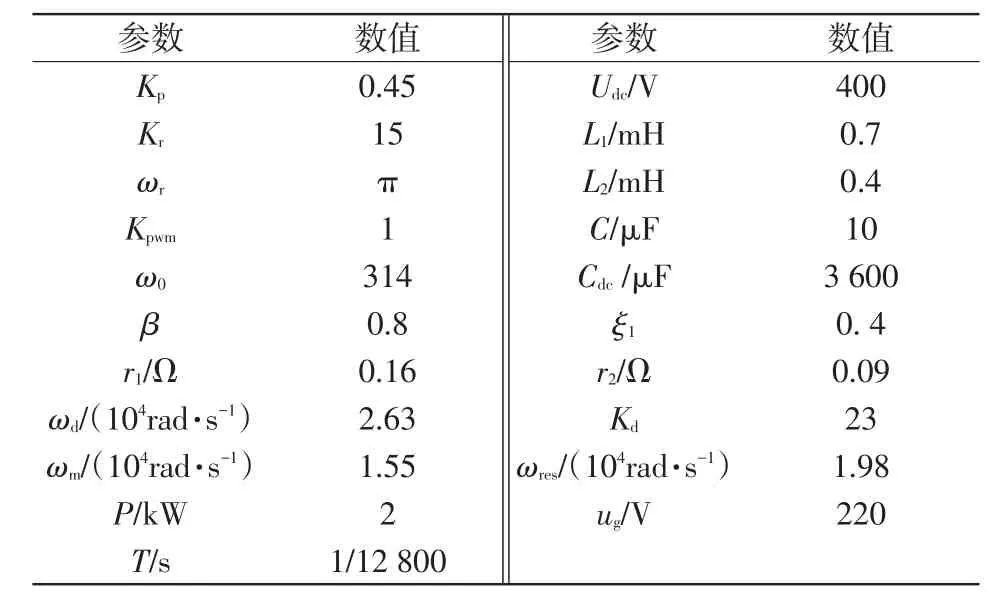
表3 系统参数Tab.3 System parameters

选取Kp=0.45，Kr=15，ωr= π，环路增益的波特图如图7所示，其中相位裕度PM为47.9°，稳定裕度满足工程应用的需要。

加入微量扰动信号19 800 rad/s和15 500 rad/s，验证系统的谐振抑制效果以及稳定性能。图8（b）～8（d）分别为β=2.88ξ1、β=2.00ξ1、β=1.62ξ1条件下并网电流ig的稳态仿真波形。并网电流ig波形趋于光滑，谐振尖峰得到抑制，且在β=2ξ1时谐振尖峰已被很好地抑制。图9为基于图8（c）、8（d）参数下并网电流的动态仿真波形，其中为并网指令电流。根据图9可知，β=2ξ1时系统峰值时间小，过渡过程更加快速平滑，能够更好地跟踪指令电流，系统基于β=2ξ1处性能最佳。

图7 环路增益的波特图Fig.7 Bode diagram of loop gain

图8 引入扰动信号并网电流ig的稳态仿真波形Fig.8 Steady-state simulation waveform of grid-connected current igafter the introduction of disturbance signal

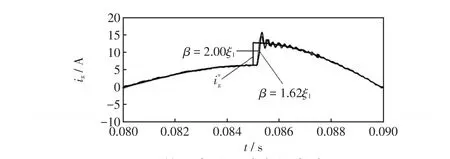
图9 并网电流ig动态仿真波形Fig.9 Dynamic simulation waveform of grid-connected current ig

在实验室搭建了一台基于DSP2812控制的2 kW单相LCL型逆变器样机，如图10所示。功率器件选用IPM模块PM505LA060，最高开关频率可达20 kHz，DSP采用TMS320F2812，样机参数如表3所示。

图10 2 kW单相LCL型逆变器实物照片Fig.10 Photo of prototype of 2 kW single-phase LCL-type inverter

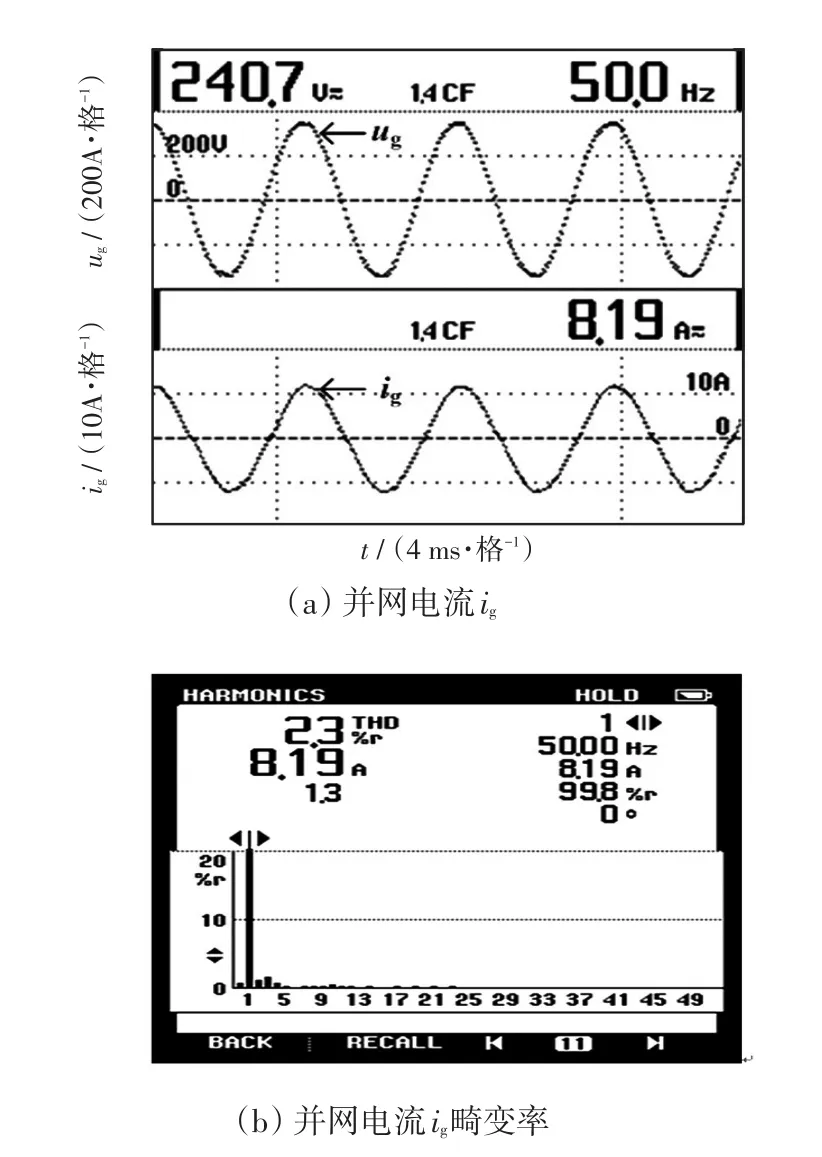
图11 满载并网电流的实验结果Fig.11 Experimental result of grid-connected current under full load condition

图11为GCFAD优化策略下的并网电流波形和谐波分析。并网功率因数PF达到0.998，并网畸变率仅为2.3%，远低于国家标准5%，能够实现将较好电能质量的有功功率馈入电网。图12为采用高速数字示波器DPO3032观测不同β/ξ1下并网电流的动态实验波形，图12（a）对应的超调量低于图12（b）中的超调量。当β/ξ1=2.00时，系统在暂态过程的超调量仅为8%，使得并网电流波形在突变后的下一个工频周期便能稳定运行，具有更快的响应速度与更小的超调量，系统具备很好的稳态和动态性能。

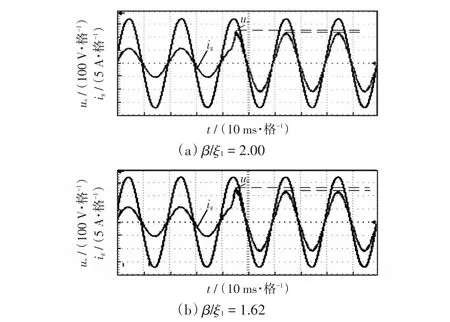
图12 不同β/ξ1下并网电流的动态实验波形Fig.12 Dynamic experimental waveforms of grid-connected current with different values of β/ξ1

5 结 论

本文提出了一种单相LCL型并网逆变器的GCFAD优化设计方法，得出以下结论。

（1）GCFAD等效在滤波电容支路并联上一个虚拟电容与电阻，虚拟电阻增加系统阻尼，虚拟电容降低系统谐振频率。

（2）基于等效虚拟阻抗模型及劳斯稳定判定，得到系统动态性能指标与GCFAD参数的本质联系。增大Kd或减少ωd可提高对LCL滤波器谐振尖峰的抑制能力；减少Kd或ωd可提高系统动态响应速度。若仅考虑参数ωd，其值越小系统动态性能越好。

（3）建立零极点模型中，当β/ξ1=2时，系统处于最佳工作状态。

[1]李振文，陈宏，熊尚峰，等（Li Zhenwen，Chen Hong，

Xiong Shangfeng，et al）.考虑分布式发电和联络线的配电网扩展规划（Expansion planning for distribution network considering DG and tie-lines）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2016，28（1）：63-67.

[2]吴磊，廖秋萍，吕 林，等（Wu Lei，Liao Qiuping，Lü Lin，et al）.含分布式发电配电网故障区间定位的新方法（New approach of fault section location in distribution network with DG）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（5）：92-96，102．

[3]Mohamed Y A-R I，A-Rahman M，Seethapathy R.Robust line-voltage sensorless control and synchronization of LCL-filtered distributed generation inverters for high power quality grid connection[J].IEEE Trans on Power Electronics，2012，27（1）：87-98.

[4]Gabe I J，Montagner V F，Pinheiro H.Design and implementation of a robust current controller for VSI connected to the grid through an LCL filter[J].IEEE Trans on Power Electronics，2009，24（6）：1444-1452.

[5]Liserre M，Blaabjerg F，Teodorescu R.Grid impedance estimation via excitation of LCL-filter resonance[J].IEEE Trans on Industry Applications，2007，43（5）：1401-1407.

[6]汪玉风，宋雪萍，郝辉，等（Wang Yufeng，Song Xueping，Hao Hui，et al）.SAPF并网滤波器RC并联LCL增阻尼新方法（New method to increase damping of RC parallel LCL filter for grid-connected SAPF）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（8）：19-24.

[7]Malinowski M，Szczygiel W，Kazmierkowski M P，et al.Sensorless operation of active damping methods for threephase PWM converters[C]//IEEE International Symposium on Industrial Electronics.Dubrovnik，Croatia，2005：775-780.

[8]伍小杰，孙蔚，戴鹏，等（Wu Xiaojie，Sun Wei，Dai Peng，et al）.一种虚拟电阻并联电容有源阻尼法（An active damping method of virtual resistor in parallel with capacitor）[J].电工技术学报（Transactions of China Electrotechnical Society），2010，25（10）：122-128.

[9]王学华，阮新波，刘尚伟（Wang Xuehua，Ruan Xinbo，Liu Shangwei）.抑制电网背景谐波影响的并网逆变器控制策略（Control strategy for grid-connected inverter to suppress current distortion effected by background harmonics in grid voltage）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（6）：7-14.

[10]Wu Eric，Lehn P W.Digital current control of a voltage source converter with active damping of LCL resonance[J].IEEE Trans on Power Electronics，2006，21（5）：1364-1373．

[11]Liserre M，Dell’Aquila A，Blaabjerg F.Stability improvements of an LCL-filter based three-phase active rectifier[C]//33th Annual IEEE Power Electronics Specialists Conference.Cairns，Australia，2002：1195-1201．

[12]Kazmierkowski M P，Malesani L.Current control techniques for three-phase voltage source PWM converters：A survey[J].IEEE Trans on Industrial Electronics，1998，45（5）：691-703.

[13]陈东，张军明，钱照明（Chen Dong，Zhang Junming，Qian Zhaoming）.带LCL滤波器的并网逆变器单电流反馈控制策略（Single current feedback control strategy for gridconnected inverters with LCL filters）[J].中国电机工程学报（Proceedings of the CSEE），2013，33（9）：10-16.

[14]王要强，吴凤江，孙力，等（Wang Yaoqiang，Wu Fengjiang，Sun Li，et al）.带LCL 输出滤波器的并网逆变器控制策略研究（Control strategy for grid-connected inverter with an LCL output filter）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（12）：34-39．

[15]王颖杰，伍小杰，戴鹏，等（Wang Yingjie，Wu Xiaojie，Dai Peng，et al）.采用参数辨识及新型主动阻尼控制的LCL滤波脉宽调制整流器（PWM rectifier with LCL filter based on parameter identification and a new active damping control）[J].中国电机工程学报（Proceedings of the CSEE），2012，32（15）：31-39.

[16]许津铭，谢少军，肖华锋（Xu Jinming，Xie Shaojun，Xiao Huafeng）.LCL滤波器有源阻尼控制机制研究（Research on control mechanism of active damping for LCL filters）[J].中国电机工程学报（Proceedings of the CSEE），2012，32（9）：27-33．

[17]Xu Jinming，Xie Shaojun，Tang Ting.Active dampingbased control for grid-connected LCL-filtered inverter with injected grid current feedback only[J].IEEE Trans on Industrial Electronics，2014，61（9）：4746-4758.

[18]周乐明，罗安，陈燕东，等（Zhou Leming，Luo An，Chen Yandong，et al）.单相LCL型并网逆变器功率控制及有源阻尼优化方法（A single-phase grid-connected power control and active damping optimization strategy with LCL filter）[J].电工技术学报（Transactions of China Electrotechnical Society），2016，31（6）：144-154.

[19]范宝奇，罗晓曙，廖志贤，等（Fan Baoqi，Luo Xiaoshu，Liao Zhixian，et al）.神经网络准PR光伏并网逆变器控制技术（Quasi PR photovoltaic grid-connected inverter control method based on BP neural network）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2016，28（3）：30-34．

Optimized Design Method of Grid Current Feedback Active Damping for LCL-type Grid-connected Inverter

WANG Ying1，ZHOU Leming2
（1.Hunan Post and Telecommunication College，Changsha 410015，China；2.National Electric Power Conversion and Control Engineering Technology Research Center，Changsha 410082，China）

Considering that there are two inter-constrained parameters in the resonance-peak suppression degree and response speed for the grid current feedback active damping（GCFAD）method，which is harmful for improving the dynamic performance of the LCL-type grid-connected inverter，an equivalent virtual impedance model is established to illustrate the essential relationship between the system dynamic performance indicators and GCFAD parameters.Moreover，with the combination of zero-pole model and the Routh-Hurwitz stability criterion，an optimized design method of GCFAD is proposed to improve the dynamic performance of the LCL-type grid-connected converter.The proposed design method can reduce the two variables of GCFAD to a single one，which reduces the complexity of parametric design；it also decouples the two inter-constrained parameters，which leads to the best dynamic performance of the control system.Simulation and experimental results show that with the proposed design method，the current distortion rate of LCL-type grid-connected converter is only 2.2%under full load condition；when the system jumps from a half load to a full load，the system overshoot is only 8%，indicating a faster response speed and a smaller overshoot comparatively.

grid-connected inverter；LCL filter；active damping；digital high-pass filter；dynamic performance

TM46

A

1003-8930（2017）10-0130-08

10.3969/j.issn.1003-8930.2017.10.022

2016-06-02；

2017-07-11

汪 英（1972—），女，硕士，副教授，研究方向为电力电子技术、电子技术、物联网应用技术。Email：wangying_only@163.com

周乐明（1989—），男，博士研究生，研究方向为分布式发电、微电网控制和电能质量控制。Email：leming_zhou@126.com