基于广域测量信号和射影控制的多通道PSS设计

张春秋，杨洪耕，魏 亮

（1.四川大学电气信息学院，成都 610065；2.秦皇岛市供电公司，秦皇岛 066000）

基于广域测量信号和射影控制的多通道PSS设计

张春秋1，杨洪耕1，魏 亮2

（1.四川大学电气信息学院，成都 610065；2.秦皇岛市供电公司，秦皇岛 066000）

传统电力系统稳定器大多采用本地信号作为反馈输入且多为多模块级联控制结构，自由度、鲁棒性均具有局限性。为了提高其抑制系统低频振荡的能力，提出了一种基于广域测量信息和射影定理的多通道电力系统稳定器设计方法。本文采用具有高精度的TLS-ESPRIT算法辨识系统模型，并根据辨识结果分别在全系统为不同的振荡模态选择可观性及可控性均较强的信号作为控制器的反馈输入。而后，通过带通滤波器分离系统模态，并基于射影定理对各个模态分别设计控制器，实现各个模态间的分层控制。同时设计固定时滞补偿环节，以消除广域信号时滞对于控制效果的影响。最后，再次设计了传统电力系统稳定器与之进行比较。仿真实验表明，所设计的控制器较传统电力系统稳定器有更好的控制效果，且控制器阶数较低，鲁棒性强，适于工程实践。

低频振荡；电力系统稳定器；广域测量信号；射影控制；多通道；时滞

近年来，在全国电网互联的大背景下，我国电网规模不断扩大，结构日趋复杂，低频振荡日益成为严重威胁电网动态安全稳定的突出问题[1-2]。电力系统稳定器PSS（power system stabilizer）因其结构简单，经济性好，且可以从源头上消除产生负阻尼的根源[3]，目前已经成为应用最为广泛的低频振荡抑制手段[1，4]。但是传统PSS自由度低、鲁棒性差，控制效果一般，南方电网所安装的PSS已经超过300台，但是低频振荡仍时有发生。因此，设计新型的电力系统稳定器成为众多学者的研究热点。

许多研究者尝试将模糊控制[5-8]、自适应控制[8-10]、变结构控制[11-12]、粒子群算法[12]等先进的控制理论或优化算法应用于PSS设计，这在一定程度上提高了PSS的控制效果。文献[7]根据模糊控制理论，利用MATLAB工具箱设计了一种模糊电力系统稳定器，但是所设计的PSS稳态性能较差；文献[8]结合模糊控制和自适应控制，克服了普通公式型模糊算法的缺点，设计了一种自寻优模糊电力系统稳定器；文献[12]设计了一种直接作用于发电机调速器的 GPSS（governor power system stabilizer），达到了抑制低频振荡的目的；文献[13]则是采用改进的微粒群优化算法对传统PSS进行参数优化，有效地提高了测试系统的鲁棒性。

以上设计方法，在一定程度上均达到了优化系统阻尼、抑制低频振荡的目的，但是均属于本地控制策略，所设计PSS自由度低、区域协调能力差。随着广域测量系统WAMS（wide-area measurement system）的快速发展，引入远端优选信号作为PSS的反馈输入成为可能[14-16]。文献[17]基于系统留数矩阵设计了一种广域PSS，达到了更好的控制效果。但是所设计PSS仍然采用多模块级联控制结构，鲁棒性差且参数整定困难，同时文中并未考虑广域信号传递过程中时滞对于控制效果的影响。采用广域信息可有效地提高大型互联电网的动态性能[18-22]，但是远距离信号传输的时间延迟不可忽略[21]。

针对上述研究的不足，本文提出了一种基于广域测量信号和射影定理[23]的多通道电力系统稳定器。针对系统的每一种振荡模态，分别采用留数法在全系统选择可观性及可控性均较强的信号作为控制器的反馈输入，并基于射影定理[23]从系统状态方程出发对系统各个模态分别设计输出反馈控制器和时滞补偿环节，实现各个模态间的分层控制。同时，设计了传统的电力系统稳定器与多通道电力系统稳定器进行比较。仿真实验表明，所设计的控制器较传统电力系统稳定器有更好的控制效果，且控制器阶数较低，鲁棒性强，易于工程实现。

1 射影控制原理

1.1 射影定理

在实际工程中，一般难以实现全状态反馈控制器的构建，而基于射影定理获得其低阶等效输出反馈控制器是解决这一问题的有效途径[23-25]。本文采用TLS-ESPRIT算法辨识出系统准确模型，并基于射影定理通过保留系统主导特征值，将系统全状态反馈控制器映射为低阶的输出反馈控制器[25]，进行PSS设计。

设被控系统的状态方程为

式中：x为状态向量；y为输出向量；u为输入向量；A为状态矩阵；B为控制矩阵；C为输出矩阵。

假设系统是状态完全可控的，设系统的状态反馈增益向量为K，状态反馈控制公式为

将系统方程改写为

对加入状态反馈后的系统进行特征值分解，即

式中：Λ为系统全部特征值所构成的对角矩阵；X为与Λ所对应的特征向量构成的矩阵。

设所求射影控制器的状态方程为

式中：z为所求控制器状态向量；Au、Bu和Cu分别为所求控制器的状态矩阵、控制矩阵及输出矩阵。

联立式（1）和式（5）可得

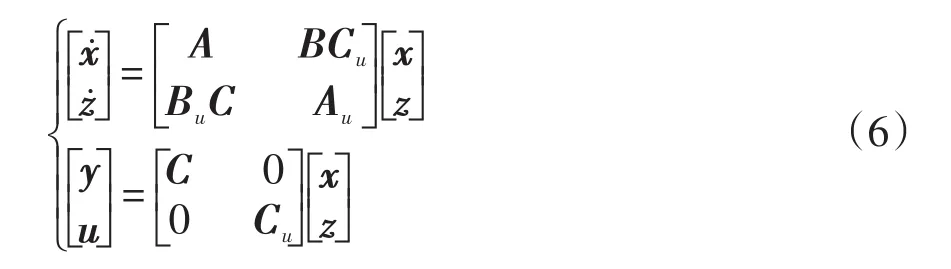
对增广状态矩阵进行特征值分解

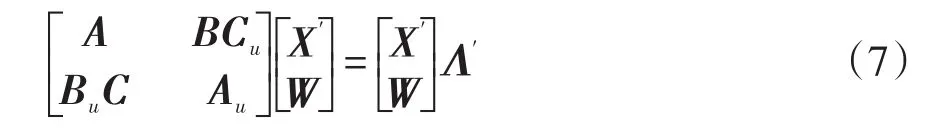
式中：W为因闭环系统阶数增加而引入的矩阵，它代表了控制器的状态空间变换；Λ′为式（3）系统主导特征值的保留值；X′为与Λ′对应的特征向量所构成的矩阵。故有

由式（7）可得

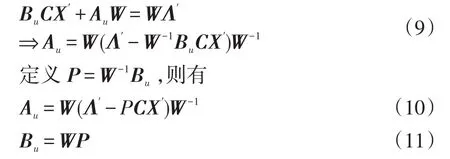
鉴于Λ′是式（3）系统主导特征值的保留值，所以由式（7）和式（8）联立可得

求得

考虑到W仅代表控制器的引入对特征向量的一种的状态空间转换，因此W可为任意可逆矩阵。令W为单位矩阵。而矩阵P是一个可以自由调节的矩阵[22-24]，因此可以通过调节矩阵P来使闭环系统具有较为理想的阻尼比。

结合式（10）、式（11）及式（13）可知，只需求得系统状态反馈增益向量K，即可求得射影控制器的各状态空间矩阵，进而求得控制器传递函数。

1.2 基于阿克曼公式求反馈增益矩阵

假设式（3）中闭环系统期望的极点位置分别为s=u1，s=u2，…，s=un。那么，系统的特征方程为

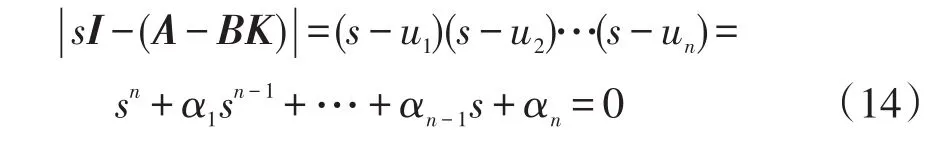
式中：α1，α2，…，αn为相关系数；I为单位矩阵。则第1.1节中所求的状态反馈增益向量K可以通过阿克曼公式[26]求得

式中，φ(A)=An+α1An-1+…+αn-1A+αnI。

2 基于TLS-ESPRIT算法的系统辨识

TLS-ESPRIT算法是一种基于线性化近似的高精度信号分析方法。与传统辨识算法相比，具有抗噪抗干扰能力更强、计算量更少、模态参数辨识精度更高的优点[27]。TLS-ESPRIT算法的关键是将采样数据构成Hankel矩阵，进而计算出信号的旋转因子，通过旋转因子即可求出信号的频率和衰减因子，最后结合最小二乘法求出信号的幅值与相位[27-29]。

2.1 系统模态辨识

基于PSCAD/EMTDC所搭建的某实际电网仿真网络结构如图1所示。在搭建电磁暂态模型时，主要考虑送端系统中的500 kV线路，对于220 kV线路及相关负荷进行等值处理。系统运行方式为，电厂A和电厂C各开两台600 MW汽轮发电机组，电厂B开一台600 MW汽轮发电机；直流系统单极降功率（1 600 MW）运行，控制方式为整流侧定电流控制、逆变侧定熄弧角控制。

图1 某实际电网仿真网络结构Fig.1 Network structure of a real power grid in simulation

在系统进入稳态运行后，对其施加不影响系统线性化条件的小幅值扰动。扰动施加地点为直流系统定电流控制器处，扰动形式为低幅值阶跃输入，将电厂A中1号机组频率偏差作为振荡信号进行提取。应用TLS-ESPRIT算法对所提取信号进行模态辨识，结果如表1所示。

表1 电厂A中1号机组振荡模态Tab.1 Oscillation modes of No.1 machine in plant A

由表1可知，系统中存在0.746 Hz和1.244 Hz两个低频振荡模态，且两种模态均属于弱阻尼振荡模式。

2.2 基于留数法的反馈信号选择

随着20170802WAMS的发展，各种反馈控制器的输入信号不再局限于本地信号。对于图1系统，电厂A中1号机组PSS的待选反馈输入信号包括系统内所有发电机组的转速差 Δωi（i=1，2，…，5）。在进行反馈信号选择时，应尽量使反馈信号对于目标模式具有很强的控制能力[16]。留数是反映可观性和可控性的综合性指标[30]，能够衡量出控制器对于相应模态的影响程度。所以应尽量选择对于目标模式留数较大的反馈信号。

对于式（1）中的被控系统，将其转换为频域形式得

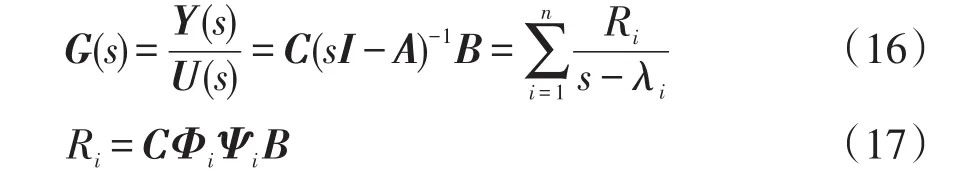
式中：λi为系统特征值；Ri为特征值所对应的留数，综合反映信号对于相应模态的可控性与可观性[16]；Φi和Ψi分别为特征值对应的左、右特征向量。

应用TLS-ESPRIT算法进行系统振荡模态辨识时，可以直接辨识出图1系统的传递函数，通过“系统传递函数”与“系统状态空间描述”之间的转换关系即可得到矩阵A、B、C。随后即可计算出其左、右特征向量。

为了进行PSS广域反馈信号选取，需要辨识系统中所有发电机转速偏差相对于电厂A中1号机组励磁参考电压的传递函数。在系统进入稳态运行后，对其施加不影响系统线性化条件的小幅值扰动。以电厂A中1号机组励磁电压参考信号低幅值阶跃扰动Δuref为输入信号，以系统中各台发电机转子角速度增量Δωi为输出，分别得到各发电机组转速偏差信号相对于1号机组励磁参考电压的降阶模型。根据所辨识的传递函数，按照式（17）分别计算出其留数如表2所示。

表2 反馈信号留数辨识结果Tab.2 Recognition result of residues in feedback signals

由表2可知，对于模态1留数较大的反馈信号为Δω4，因此选择Δω4作为模态1的反馈信号；同理，对于模态2，选择留数最大的Δω1作为反馈输入信号。

3 控制器设计

3.1 控制器结构

为了消除不同振荡模态间的影响，在控制器中加设带通滤波器，对不同的振荡模式分别设计射影控制器Gmodi，抑制模式间的相互影响，进而实现控制目标。控制器被设置在电厂A的1号机组上，其结构如图2所示。

图2 多通道PSS结构Fig.2 Structure of multi-channel PSS

不同控制通道的输入信号分别通过留数法在全系统寻优获得；控制器的滤波环节采用Butterworth滤波器；对于采用广域信号的通道，时滞补偿环节采用相位补偿环节来实现[16]，以消除信号时滞对于控制效果的不良影响，其传递函数为

式中：KT为比例系数；α、β为补偿因子。

3.2 控制器设计

根据表2辨识结果，振荡模态1选择Δω4为广域反馈信号，振荡模态2选择本地信号Δω1为反馈信号。以直流系统整流侧定电流控制信号的低幅值阶跃扰动为输入，电厂A中1号机组频率偏差为输出，采用TLS-ESPRIT算法[26-29]辨识出两个振荡模态频率作为控制器输入时，所对应的系统传递函数为

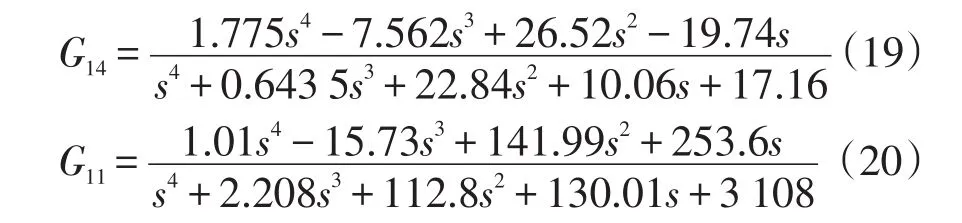
根据辨识出的不同模态下的系统传递函数，分别选择闭环系统的期望特征值，利用阿克曼公式求得相应的状态反馈增益向量

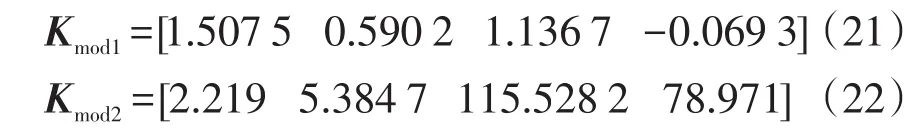
基于状态反馈向量式（21）和式（22），结合射影定理和控制效果，对矩阵P进行数值选择，得到结果为

此时求出的两种模态下控制器的传递函数为

由于模态2采用本地信号作为反馈输入，所以只需对模态1控制通道进行时滞补偿。目前国内外正在运行的WAMS实测时滞大约为60～80 ms[19-22]，因此控制器时滞按80 ms进行校正。校正环节在系统振荡频率附近大概需要产生28°的超前相位补偿[26]，由此计算时滞补偿环节传递函数为

设计出多通道广域PSS后，为与传统PSS进行比较，再次设计图3所示传统电力系统稳定器。基于第2.2节所辨识出的传递函数，根据相位补偿法设计传统PSS，其参数如表3所示。

图3 传统PSS结构Fig.3 Structure of conventional PSS

表3 传统PSS参数Tab.3 Parameters of conventional PSS

4 仿真验证

将设计的多通道广域PSS和传统PSS分别配置到电厂A中1号机组，施加不同的扰动在PSCAD/EMTDC中进行验证。

4.1 交流侧三相短路故障

以最为严重的三相短路故障为例进行说明：设置2 s时刻节点A至节点B两回交流线路中的某一回线在节点B侧10%处发生三相短路故障，故障后0.1 s故障消除。分别配置不同电力系统稳定器时，交流系统频率变化情况如图4所示。由图4可知，在系统发生三相短路故障后，系统低频振荡模态将被激发，系统失稳。此时，两种PSS均可以有效抑制系统低频振荡，但是本文所设计的多通道广域PSS控制周期更短、鲁棒性更强，控制效果远远优于传统PSS。

图4 三相短路故障时，配置不同PSS系统频率变化Fig.4 Changes of system frequency with different PSSs under three-phase short circuit fault

4.2 直流侧功率紧急提升

设置直流系统在2 s时刻紧急功率提升0.05 p.u.。此时，分别配置不同电力系统稳定器时，观测到的交流系统频率变化情况如图5所示。

图5 直流功率提升5%时，配置不同PSS系统频率变化Fig.5 Changes of system frequency with different PSSs when the DC power increases by 5%

由图5可知，当直流系统功率紧急提升时，系统低频振荡模态将被激发。传统PSS可以有效抑制系统低频振荡，但是抑制周期长，鲁棒性不足；与之相比，加装本文所设计PSS后，机组转速第一摆虽然较大，但是仍可以更为迅速地恢复稳定，控制器鲁棒性较传统PSS得到了提高。

由上述仿真可知，利用TLS-ESPRIT算法辨识系统模型，并基于射影定理设计的多通道广域PSS，在各种故障下，均可有效地抑制系统低频振荡，保持系统稳定，且在同等情况下，控制效果优于传统PSS。

4.3 广域信号对控制效果的影响

为了体现本文采用广域信号对控制效果的影响，重新设计多通道PSS。模态2控制通道保持不变，模态1控制器采用本地发电机转速差信号Δω1作为输入信号重新进行控制器设计。再次设计第4.1节中的三相短路故障进行仿真实验。仿真结果如图6所示。

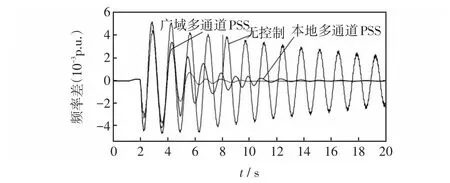
图6 三相短路故障时，配置不同控制信号的PSS系统频率变化Fig.6 Changes of system frequency with PSSs of different control signals under three-phase short circuit fault

其中，广域多通道PSS模态1采用广域信号Δω4为反馈输入，模态2采用本地信号Δω1作为反馈信号；本地多通道PSS的两个模态均采用本地信号Δω1作为反馈信号。与第4.1节中情况类似，在系统发生三相短路故障后，系统低频振荡模态将被激发，系统失稳。此时，两种PSS在一定程度上均可以抑制系统的低频振荡。但是采用广域信号的PSS抑制周期更短，控制效果更佳，说明采用广域信号可以达到更好的控制效果。

4.4 时滞对控制效果的影响

本文PSS设计中采用相位超前环节进行固定时滞补偿，为研究此策略对消除时滞影响的有效性，分别设置反馈信号的不同时滞情况，进行故障仿真。仿真故障与第4.1节相同，以交流系统频率信号作为观测信号，仿真结果如图7所示。

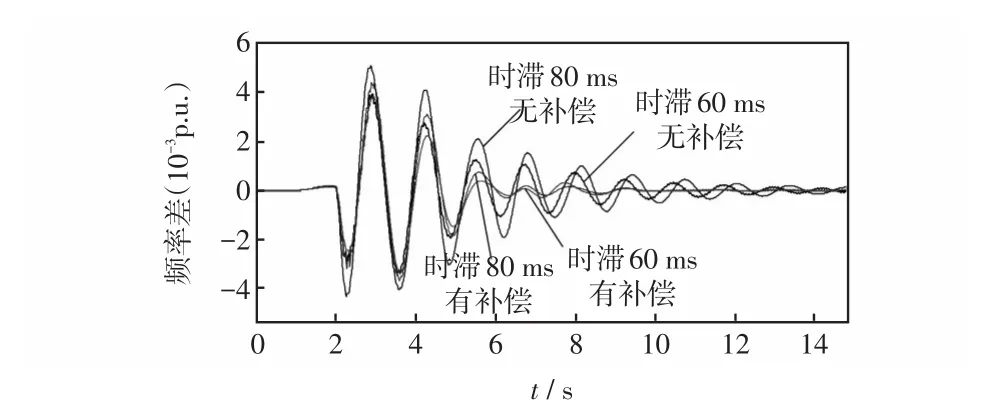
图7 不同时滞情况下系统频率变化Fig.7 Changes of system frequency under different time delays

由图7可知，当无时滞补偿环节时，信号时滞所引起的相位滞后会严重恶化PSS的控制效果；而加装时滞补偿环节后，在不同时滞条件下，PSS均可以达到较好的控制效果，说明本文所采用的时滞补偿措施对于消除时滞影响具有较好的效果。

5 结 论

本文基于广域测量信号和射影定理设计了一种多通道PSS，在PSCAD/EMTDC中结合某实际电网运行算例进行研究，得出以下结论。

（1）采用广域信号作为PSS反馈输入信号，能够以最小的控制代价获得最优的阻尼效果，同时提高了控制器的自由度和区域协调能力；采用留数法在全系统选择最佳反馈信号，在有效减小计算量的同时，综合考虑了反馈信号能观性和能控性指标；广域信号传输所造成的时滞不可忽略，时滞补偿环节的设计可以有效地消除其不良影响。

（2）基于射影定理通过保留系统主导特征值，将系统全状态反馈控制器映射为低阶的输出反馈控制器，不仅比传统控制器具有更好的控制效果与鲁棒性而且有利于工程实际。

（3）利用带通滤波器分离不同振荡模态，对各个模态分别设计射影控制器，为不同频段的振荡分别提供恰当的阻尼，有助于消除控制器间的交互影响，实现了不同模态间的分层控制，能够达到更好的控制效果。

（4）利用高精度辨识算法通过非线性时域仿真直接导出系统精确的低阶线性化模型，解决了实际电网复杂网络拓扑和多变工况所带来的数学建模难题，对于实际电网控制器设计具有参考意义。

（5）电力系统稳定器、直流调制、FACTS装置等均是抑制系统低频振荡的有效措施，但是目前关于多种控制手段间的协调控制方法研究较少，可作为下一步的研究重点。

[1]宋墩文，杨学涛，丁巧林，等（Song Dunwen，Yang Xuetao，Ding Qiaolin，et al）.大规模互联电网低频振荡分析与控制方法综述（A survey on analysis on low frequency oscillation in large-scale interconnected power grid and its control measures）[J].电网技术（Power System Technology），2011，35（10）：22-28．

[2]鲍颜红，王永昆，方勇杰，等（Bao Yanhong，Wang Yongkun，Fang Yongjie，et al）.基于广域测量信息和直流功率支援的低频振荡抑制方法（DC power support for damping low frequency oscillations based on WAMS）[J].电力系统自动化（Automation of Electric Power Systems），2013，37（21）：118-122．

[3]朱方，赵红光，刘增煌，等（Zhu Fang，Zhao Hongguang，Liu Zenghuang，et al）.大区电网互联对电力系统动态稳定性的影响（The influence of large power grid interconnected on power system dynamic stability）[J].中国电机工程学报（Proceedings of the CSEE），2007，27（1）：1-7．

[4]王青，孙华东，马世英，等（Wang Qing，Sun Huadong，Ma Shiying，et al）.电力系统小干扰稳定安全评估的一般原则及其在贵州电网中的应用（General principle of power system small signal stability evaluation and its application in Guizhou power grid）[J].电网技术（Power System Technology），2009，33（6）：24-28．

[5]Hussein T，Saad M S，Elshafei A L，et al.Damping interarea modes of oscillation using an adaptive fuzzy power system stabilizer[J].Electric Power Systems Research，2010，80（12）：1428-1436．

[6]Wang Mingdong，Liu Xianlin，Yu Jilai.Modified GA based optimization design of fuzzy governor power system stabilizer for hydro-generator unit[J].Istanbul University-Journal of Electrical and Electronics Engineering，2008，8（2）：607-616．

[7]丁峰，赵书强，王哲（Ding Feng，Zhao Shuqiang，Wang Zhe）.模糊电力系统稳定器的设计与实现（Design and implementation of fuzzy power system stabilizer）[J].电力自动化设备（Electric Power Automation Equipment），2002，22（12）：47-50．

[8]赵书强，丁峰，侯子利，等（Zhao Shuqiang，Ding Feng，Hou Zili，et al）.自寻优模糊电力系统稳定器的设计（Design of self-optimizing fuzzy power system stabilizer）[J].电工技术学报（Transactions of China Electrotechnical Society），2004，19（3）：94-96．

[9]谷志锋，朱长青，杨润生，等（Gu Zhifeng，Zhu Changqing，Yang Runsheng，et al）.全状态跟踪非线性鲁棒自适应分散励磁控制（Nonlinear robust adaptive decentralized excitation control for multi-machine power system based on all state tracking）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2016，28（2）：47-55.

[10]Pahalawatha N C，Hope G S，Malik O P，et al.Real time implementation of MIMO adaptive power system stabilizer[J].IEE Proceedings-Generation，Transmission and Distribution，1990，137（3）：186-194．

[11]Samarasinghe V G D C，Pahalawaththa N C.Stabilization of a multi-machine power system using nonlinear robust variable structure control[J].Electric Power Systems Research，1997，43（1）：11-17．

[12]林其友，陈星莺，曹智峰（Lin Qiyou，Chen Xingying，Cao Zhifeng）.多机系统调速侧电力系统稳定器GPSS的设计（Design of a governor-side power system stabilizer for multi-machine power system）[J].电网技术（Power System Technology），2007，31（3）：54-58．

[13]赵辉，刘鲁源，张更新（Zhao Hui，Liu Luyuan，Zhang Gengxin）.基于微粒群优化算法的最优电力系统稳定器设计（Optimal design of power system stabilizer using particle swarm optimization）[J].电网技术（Power System Technology），2006，30（3）：32-35．

[14]Heniche A，Kamwa I.Assessment of two methods to select wide-area signals for power system damping control[J].IEEE Trans on Power Systems，2008，23（2）：572-581．

[15]Wang Juanjuan，Fu Chuang，Zhang Yao.Design of WAMS-based multiple HVDC damping control system[J].IEEE Trans on Smart Grid，2011，2（2）：363-374．

[16]王曦，李兴源，赵睿（Wang Xi，Li Xingyuan，Zhao Rui）.基于相对增益和改进粒子群算法的PSS与直流调制协调策略（Coordination strategy of PSS and DCM based on relative gain and improved PSO）[J].中国电机工程学报（Proceedings of the CSEE），2014，34（34）：6177-6184．

[17]袁野，程林，孙元章，等（Yuan Ye，Cheng Lin，Sun Yuanzhang，et al）.基于系统留数矩阵的广域PSS设计（Wide area PSS design based on system residue matrix）[J].电力系统自动化（Automation of Electric Power Systems），2007，31（24）：1-6．

[18]刘学智，袁荣湘（Liu Xuezhi，Yuan Rongxiang）.基于输出反馈的电力系统广域阻尼控制（Output feedback based wide-area damping control for power system）[J].电网技术（Power System Technology），2010，34（4）：115-118．

[19]Kamwa I.Wide-area measurement based stabilizing control of large power systems：A decentralized/hierarchical approach[J].IEEE Trans on Power Systems，2001，16（1）：136-153．

[20]肖晋宇，谢小荣，胡志祥，等（Xiao Jinyu，Xie Xiaorong，Hu Zhixiang，et al）.基于在线辨识的电力系统广域阻尼控制（Power systems wide-area damping control based on online system identification）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（23）：22-27．

[21]王成山，石颉（Wang Chengshan，Shi Jie）.考虑时间延迟影响的电力系统稳定器设计（PSS designing with consideration of time delay impact）[J].中国电机工程学报（Proceedings of the CSEE），2007，27（10）：1-6．

[22]He J，Lu C，Wu X，et al.Design and experiment of wide area HVDC supplementary damping controller considering time delay in China southern power grid[J].IET Generation，Transmission&Distribution，2009，3（1）：17-25．

[23]李宽，李兴源，李保宏，等（Li Kuan，Li Xingyuan，Li Baohong，et al）.基于射影定理分层控制的次同步阻尼控制器设计（Design of supplementary subsynchronous damping controller based on projective theorem for hierarchical control）[J].电力自动化设备（Electric Power Automation Equipment），2015，35（2）：80-84．

[24]常勇，徐政（Chang Yong，Xu Zheng）.基于射影控制的直流输电和静态无功补偿器协调控制（Coordinate control between HVDC and SVC based on the projective control theory）[J].电网技术（Power System Technology），2006，30（16）：40-44，63．

[25]Wise K A，Nguyen T.Optimal disturbance rejection in missile autopilot design using projective controls[J].IEEE Control Systems Magazine，1992，12（5）：43-49．

[26]Katsuhiko Ogata.Modern Control Engineering[M].New Jersey：Prentice Hall，2010．

[27]王曦，李兴源，王渝红，等（Wang Xi，Li Xingyuan，Wang Yuhong，et al）.基于TLS-ESPRIT辨识的多直流控制敏感点研究（Analysis on controllability sensitive points of multi-HVDC systems based on TLS-ESPRIT method）[J].电力系统保护与控制（Power System Protection and Control），2012，40（19）：121-125．

[28]付伟，刘天琪，李兴源，等（Fu Wei，Liu Tianqi，Li Xingyuan，et al）.高压直流自适应变结构控制器设计（Design of self-adaptive variable structure controller of HVDC System）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2017，29（5）：28-34．

[29]Tripathy P，Srivastava S C，Singh S N.A modified TLS-ESPRIT-based method for low-frequency mode identification in power systems utilizing synchrophasor measurements[J].IEEE Trans on Power Systems，2011，26（2）：719-727.

[30]蒋平，叶慧，吴熙（Jiang Ping，Ye Hui，Wu Xi）.基于留数的静止同步补偿器附加阻尼鲁棒控制（Residue-based robust control method for additional damping controller of static synchronous compensator）[J].电网技术（Power System Technology），2012，36（10）：131-135．

Design of Multi-channel PSS Based on Wide-area Measurement Signals and Projective Control

ZHANG Chunqiu1，YANG Honggeng1，WEI Liang2
（1.School of Electrical Engineering and Information，Sichuan University，Chengdu 610065，China；2.Qinhuangdao Power Supply Company，Qinhuangdao 066000，China）

The degrees of freedom and robustness and the conventional power system stabilizer（PSS）are usually constrained due to its feedback input of local signals and multi-module cascaded structure.To improve its ability to suppress the low-frequency oscillation，a multi-channel PSS based on wide-area measurement signals and projective theorem is designed.The system model is identified by the high-accuracy TLS-ESPRIT algorithm.Based on the identification result，the wide area measurement signals with both higher observability and controllability are selected as the feedback input of controllers in different oscillation modes.Then，band-pass filters are adopted to separate the oscillation modes，and controllers are designed for each mode based on projective theorem，thus realizing an hierarchical control for each mode.Moreover，compensation is designed to eliminate the influence of time delays in wide-area signals on the control effect.At last，a conventional PSS is designed and compared with the designed controller.Simulation tests indicate that compared with the conventional PSS，the designed controller has better control effect，lower order of the controller and stronger robustness，which is suitable for engineering practices.

low-frequency oscillation；power system stabilizer（PSS）；wide-area measurement signal；projective control；multi-channel；time delay

TM712

A

1003-8930（2017）10-0106-07

10.3969/j.issn.1003-8930.2017.10.018

2016-08-29；

2017-08-04

张春秋（1991—），男，硕士研究生，研究方向为电能质量分析与控制、电力系统稳定与控制。Email：1107723173@qq.com

杨洪耕（1949—），男，博士，教授，博士生导师，研究方向为电能质量分析与控制、区域电压无功控制等。Email：pqlab99@126.com

魏 亮（1990—），男，硕士，助理工程师，研究方向为高压直流输电、电力系统稳定与控制。Email：willian_weiliang@163.com