基于μ综合的空空导弹驾驶仪增益调度方法研究

臧月进,陈 欣，张 民

(1.上海机电工程研究所， 上海 201109； 2.南京航空航天大学 自动化学院， 南京 210016)

【信息科学与控制工程】

臧月进1,陈 欣2，张 民2

(1.上海机电工程研究所， 上海 201109； 2.南京航空航天大学 自动化学院， 南京 210016)

在动力学特性变化范围较大的恶劣情况下，自动驾驶仪的参数必须在导弹飞行过程中进行在线调整，以适应导弹动力学特性的变化以及全包线飞行要求。常规的调整方法是选择适应不同飞行条件的一组控制器进行切换处理。切换控制结构只需保证切换中控制器的输入输出的接口一致，无需关心控制器内部状态维数[2]。但是，这类切换控制的稳定性处理异常复杂，需要设置复杂的切换规则[3]。

1 矩阵插值调度法简介

经典的调度控制器设计方法就是通过对控制器的零极点进行插值，这对于单输入单输出系统比较高效，然而对于多变量系统效率较低、代价较大，且近似误差会被无限放大，因此该插值方法对于μ综合控制器的调度并不适用。

鉴于零极点插值和传递函数系数插值的弊端，本文介绍一种新的基于控制器的状态空间实现矩阵插值的调度方法，Lawrence曾应用该方法对导弹的驾驶仪进行插值调度[4]，它是一种基于配平线性点的插值方法。

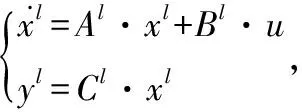
(1-g)·Al+g·Al+1

2 样例导弹μ综合控制器设计

2.1 μ综合概述

μ综合设计方法是对以参数不确定性和多点独立的有界范数不确定性描述的系统，以目标函数的结构奇异值为性能指标而形成的设计方法[5]。μ综合控制可以把稳定鲁棒性和性能鲁棒性有机地结合起来，即保证在参数摄动的情况下维持一定的鲁棒性能[6]。

典型的μ综合控制问题如图1所示，其中P为广义标称对象，K为反馈控制器，w为外部扰动，z为误差信号。

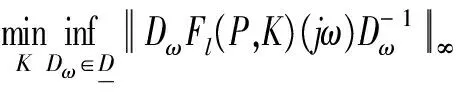
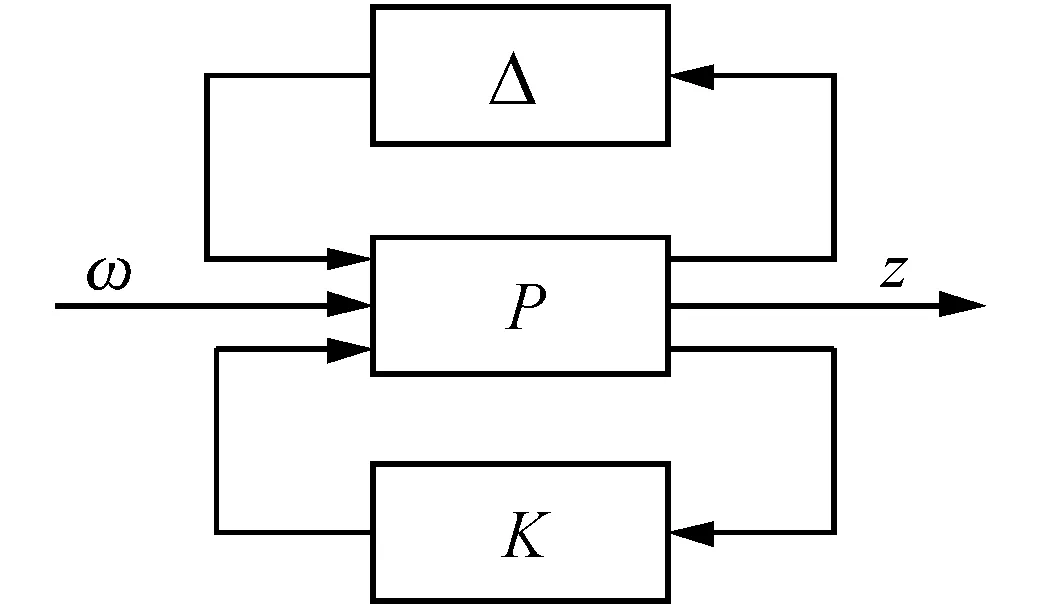
图1 μ综合控制问题的线性分式描述

2.2 导弹μ综合控制器设计

这里动压交叠区间为[ql,qu]=[95 kPa,120 kPa]，S1和S2分别是低压区和高压区对应的纵向μ综合控制器。

在某样例空空导弹的一段飞行弹道的低压区和高压区分别选择表征相应区域的特征点用于设计控制器，对非线性模型配平线性化，通过聚类筛选得到5 km高度20°攻角2 Ma速度和5 km高度30°攻角1.5 Ma速度的两个线性特征点，其模型可见文献[7]。

图2中Wideal、Win、Wact、Wn分别表示理想响应权函数，未建模不确定性规范化权函数使Δ2<1，舵机限幅权函数以及噪声权函数，Wp_lon为性能权函数，表征了系统响应的跟踪能力，Actuator为模拟的二阶舵机。

图2 纵向控制结构

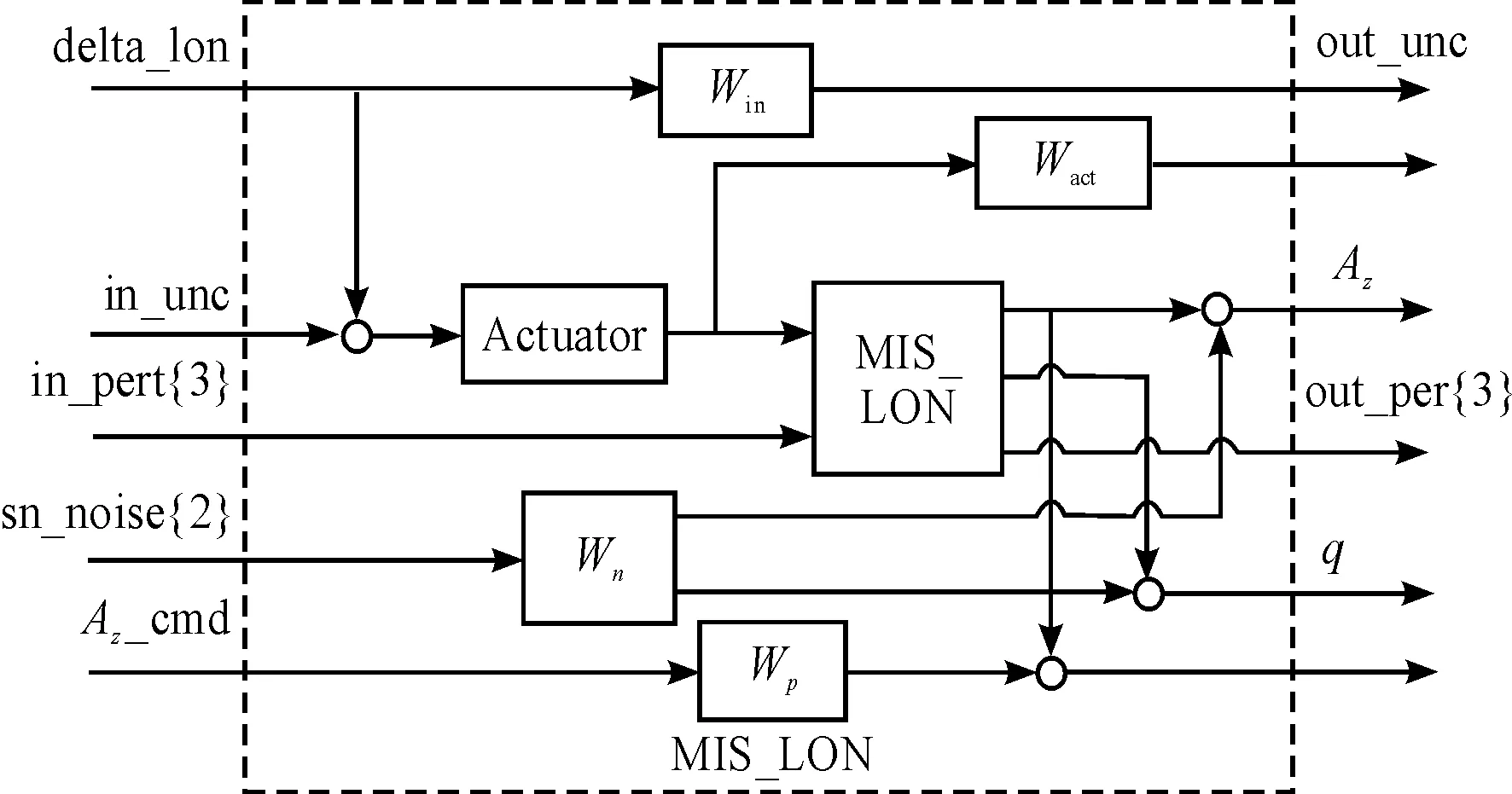
图3 纵向开环系统联接

利用Matlab的μ-toolbox进行D-K迭代[8]运算，经过3轮次迭代过程不断对D、K中参数轮流计算，得到最大结构奇异值μ为1.412 3和1.376 1，此时能够获得符合要求的17阶和19阶纵向控制器S1和S2：

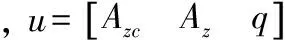
3 仿真示例与分析

本节激励指令取正负交变的单位加速度1 m/s2，对应动压区间内的适定控制器分别为17阶控制器S1和19阶控制器S2，对S2应用Hankel范数逼近降阶后，有相同的17阶，记其状态空间实现分别为[A1,B1,C1, 0]和[A2,B2,C2, 0]。

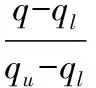
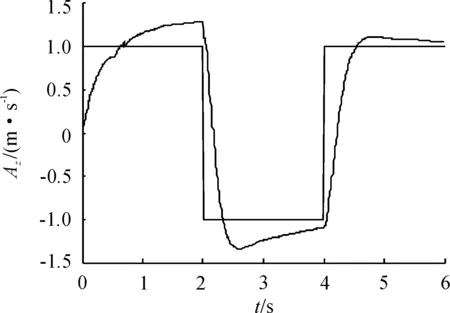
图4 状态矩阵插值调度的纵向加速度响应

图5 状态矩阵插值调度的升降舵偏角

从图4和图5看出，闭环系统对加速度指令不能完全跟踪，且升降舵偏有发散的趋势，特别地一个因控制器降阶处理后导致不同状态间插值调度失稳的情形如图6和图7所示。

图6 状态矩阵插值调度的纵向加速度响应

式(9)的矩阵插值，形式上与经典控制中的单增益插值类似，但该实现需要控制器维数保持一致，否则无法进行矩阵间的插值运算。

由2.2节的控制器设计过程可以看出，控制器阶次不可预测，可以通过Hankel范数逼近降阶法[9]处理，但这有可能造成如图6和图7所示的系统奇异失稳，在调整控制器时需极力避免。

图7 状态矩阵插值调度的升降舵偏角

鉴于状态空间矩阵插值需降阶处理，本节介绍一种插值的变化形式——对控制器的输出信号进行插值，而不是对控制器本身的插值。因为现今控制器的实现都是数字式的，故假设控制器的离散形式为K(z)，插值的离散形式如下[10-11]：

(1-g)·Kl(z)+g·Kl+1(z)·E(z)

这里g的定义与上节相同，切换变量θ的调度控制器的状态控制实现为

采用上述控制器连接结构，仍然调度上节的17阶控制器和19阶控制器，S1和S2的控制输出分别为u1和u2：

这里g同1节，即得到相应的加速度和升降舵偏角如图8和图9所示。

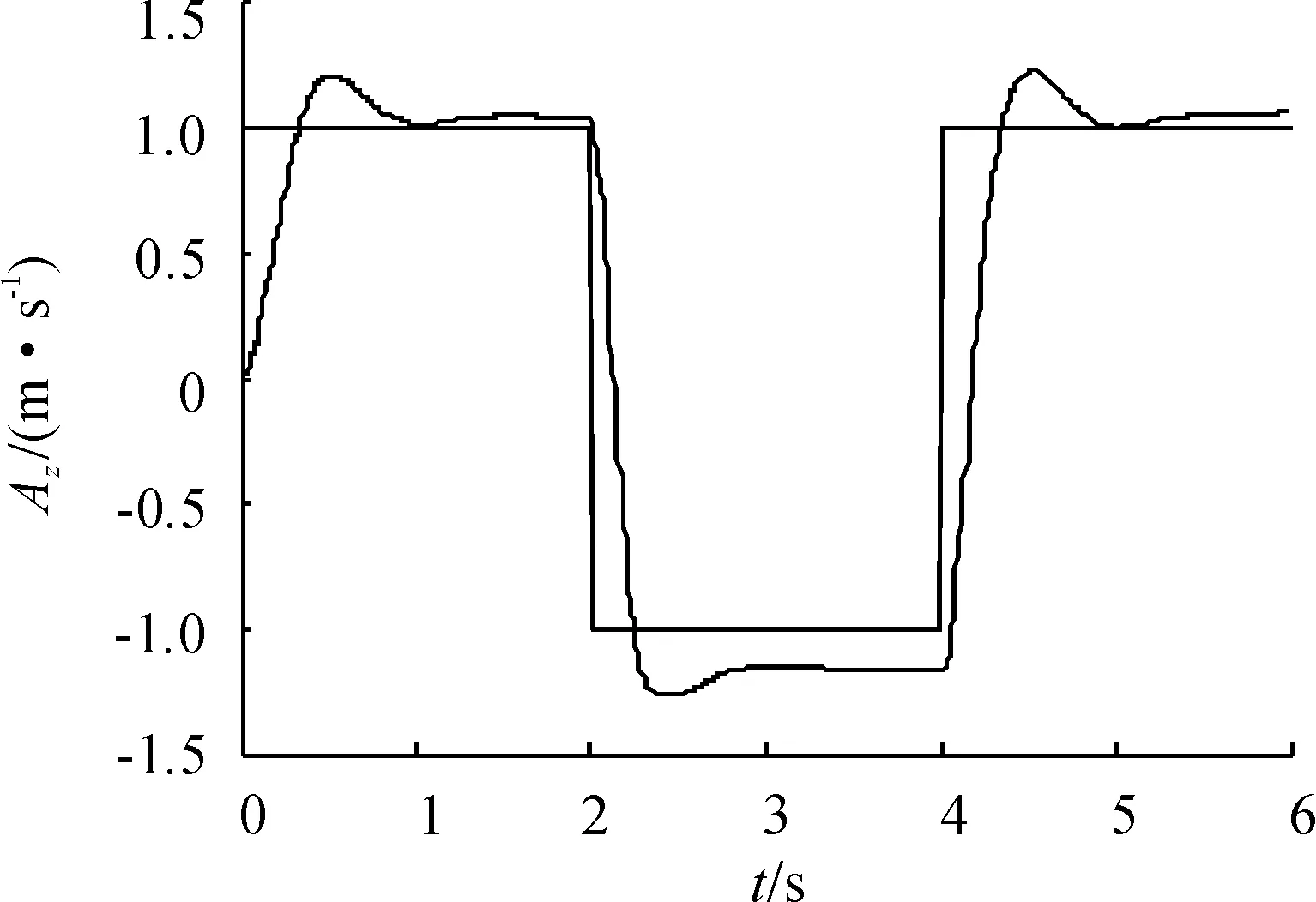
图8 控制信号插值调度的纵向加速度响应

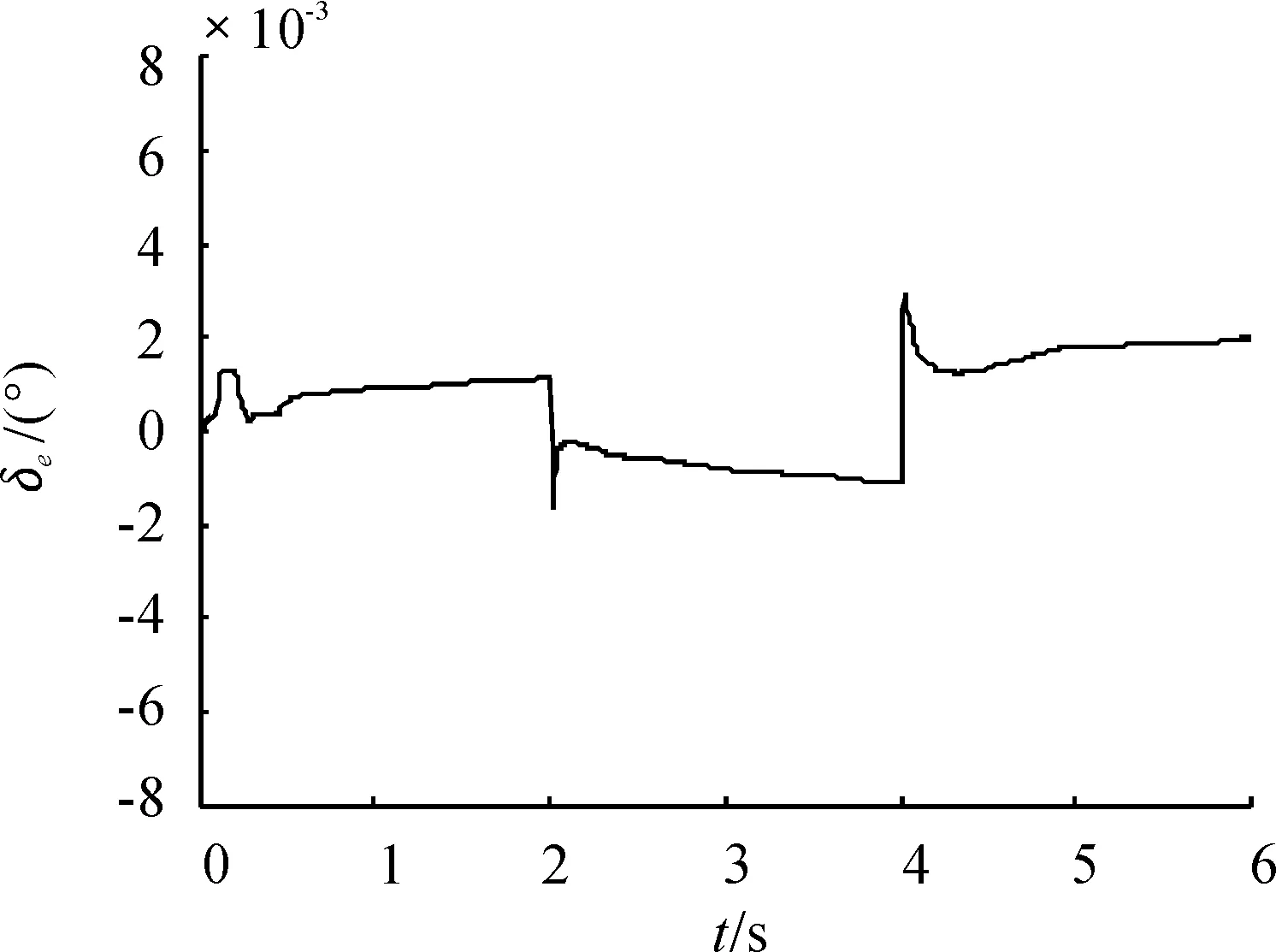
图9 控制信号插值调度的升降舵偏角

如图9所示，系统的加速度指令响应速度较快，调节时间很短，满足快速性要求，跟踪效果良好，且在控制器调整过程中没有出现任何的脉冲抖动，而升降舵偏也在容许的范围内变化。可见基于控制信号插值的调度方案实现全包线内的控制器调度没有出现奇异振荡，更为可靠。

4 结论

通过分析两种纯插值方案的诸多约束和仿真试验，可以直接调度控制器完成控制器间模态的平滑过渡并保证了驾驶仪的全包线控制能力，有力地克服了单一μ综合控制器控制全包线非线性系统的保守性。

[1] RAIMUND D,HARALD B.Flight Test of a Scheduledμ-Synthesis Autopilot for an Air-to-Air Missile[J].AIAA 2001-421.

[2] 程云龙.防空导弹自动驾驶仪设计[M].北京：国防工业出版社,1993:5-6.

[3] BRUGAROLAS P,FROMION V,SAFONOV M.Robust Switching Missile Autopilot[J].American Control Conference,1998(6):3665-3669.

[4] LAWRENCE D.A,RUGH W.J.Gain Scheduling Dynamic Linear Controllers for a Nonlinear Plant[J].IEEE Conference on Decision & Control,1993,31(3):1024-1029.

[5] 张民,陈欣,陆宇平,臧月进.基于μ综合方法的空空导弹鲁棒驾驶仪设计[J].上海交通大学学报,2011,45 (3):418-422.

[6] 张民,陈欣,陆宇平.PSO算法用于导弹鲁棒控制器性能权函数优化[J].应用科学学报,2011,29(6):650-654.

[7] 臧月进.空-空导弹μ综合控制器设计与研究[D].南京：南京航空航天大学,2012.

[8] BALAS G J,DOYLE J C,GLOVER K.The Analysis and Synthesis Toolbox[M].Math Workss and MUSYN,1991.

[10] 何素娟，张云燕，曹立学.导弹舵机MIT-Lyapunov复合控制研究[J].火力与指挥控制，2015(5):5-7.

[11] KELLY H,JOHNNY H.An Interpolation Strategy for Scheduling Dynamic Compensators[C]//AIAA-97-3764.

ResearchofGain-SchedulingofAir-to-AirMissileAutopilotBasedonμ-Synthesis

ZANG Yuejin1, CHEN Xin2, ZHANG Min2

(1.Shanghai Electro-Mechanical Engineering Institute, Shanghai 201109, China; 2.College of Automation Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China)

To overcome the conservative of one singleμ-synthesis controller to control the full envelop, dynamic pressure was employed as scheduling variable to schedule theμ-synthesis controller of the sample air-to-air missile autopilot based on interpolation method. A new scheme is presented based on interpolation control signals between design points, which avoids the restriction of controllers’ order and provides more flexible. It was proved by simulation that the new scheme achieves a smooth transition between controllers and ensures missile robust stabilization of the full envelop.

air-to-air missile;μ-synthesis; autopilot; interpolation; gain-scheduling

2017-07-13；

2017-08-11

上海市自然科学基金项目(16ZR1415900)

臧月进(1987—),男,工程师,硕士,主要从事飞行器制导控制系统研究。

10.11809/scbgxb2017.10.027

formatZANG Yuejin, CHEN Xin, ZHANG Min.Research of Gain-Scheduling of Air-to-Air Missile Autopilot Based onμ-Synthesis[J].Journal of Ordnance Equipment Engineering,2017(10):133-136.

TJ426

A

2096-2304(2017)10-0133-04

(责任编辑杨继森)