基于人工神经网络的侵彻毁伤模式识别

王 烁，石 全

(军械工程学院 装备指挥与管理系， 石家庄 050003)

【装备理论与装备技术】

基于人工神经网络的侵彻毁伤模式识别

王 烁，石 全

(军械工程学院 装备指挥与管理系， 石家庄 050003)

为了研究多因素作用下破片侵彻靶板的具体模式，利用人工神经网络方法，对输入参数进行识别，得到了相应的靶板毁伤模式。基于正交试验设计原则，利用ANSYS/LS-DYNA仿真出60组破片侵彻靶板的模式数据，作为神经网络训练的输入数据，对神经网络进行训练，另外选取3组数据作为验证数据对神经网络的训练效果进行验证。结果表明：该训练模式下，人工神经网络能够有效地识别多因素作用下破片对靶板的具体毁伤模式。

人工神经网络；侵彻模式；有限元仿真；模式识别

破片对于靶板的侵彻模式主要分为3种：侵彻、跳飞与穿透。具体的侵彻模式受到许多因素的影响，其主要影响因素为：破片的速度、入射角度、长径比、质量、靶板厚度和形状。这6个因素对于靶板损伤模式的影响各不相同，相关学者曾经进行过探讨，如米双山等[1]以等效靶板为模型研究过硬铝合金的有限元侵彻，建立了相应的相图，但相图的建立是针对弹丸特定的形状，特定的靶厚等相关固定的因素，虽然给人直观的认识，但大量固定因素反映的损伤情况有限，不能完整地反映离散情况下多不定因素对侵彻损伤的影响。为实现对输入的离散样本进行损伤模式的判定识别，本研究以人工神经网络为平台，对已得到的样本进行训练，达到对多因素的综合影响下的损伤模式进行判定的目的。

1 人工神经网络

误差反向传播神经网络BP(Error Back Propagation Neural Network)[3]是1986年由Rumelhart和Hinton提出的，它是一种能向着满足给定的输入输出关系方向进行自组织的神经网络。当输出层上的实际输出与给定的期望输出不一致时，BP算法利用输出层的误差估计输出层的直接前导层的误差，再用这个误差估计更前一层的误差。在本研究中使用MATLAB中的神经网络工具箱[4]，简化了计算，且训练效果较好。

2 MATLAB中的BP网络模型

2.1 MATLAB中BP网络传输函数常用类型

在BP神经网络中经常使用对数S形函数、正切S形函数和线性函数作为神经元的传输函数(见图1)，其函数图形和符号表示以及函数表达式分别为：

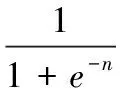
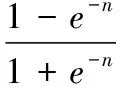
a(n)=purelin(n)=n

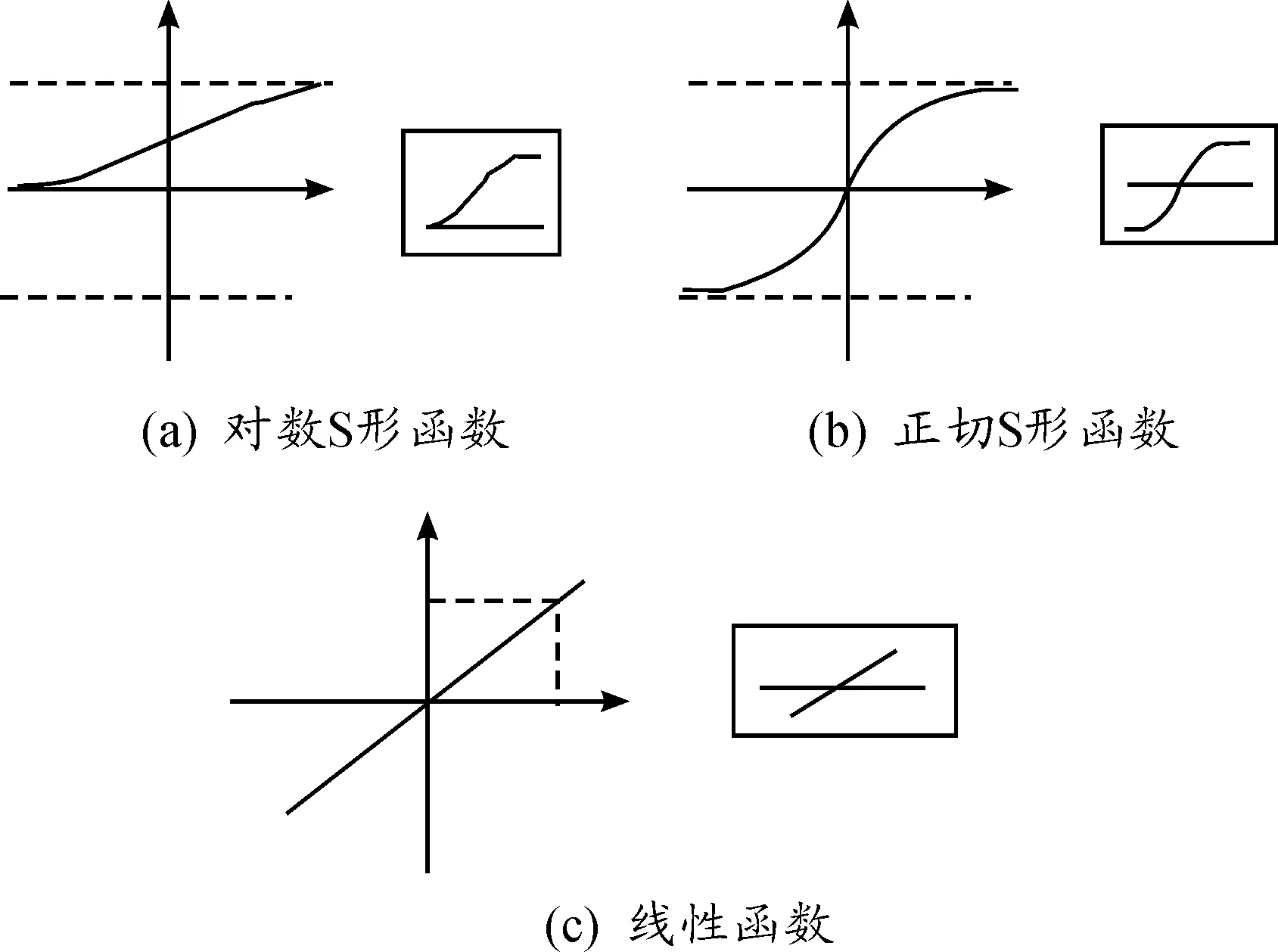
图1 常用的网络传输函数

2.2 BP网络的训练算法

神经网络需要不断地调整权值和阈值，使得网络的输入和输出满足要求的关系，这个过程往往不是一蹴而就，这种调整过程称为“训练”，而这个神经网络在训练的过程中，便具有了把输入空间映射到输出空间的能力，称之为神经网络的“学习”，调整权值和阈值的算法称之为学习规则或训练算法。主要的训练方法分为以下3种：标准BP算法(最速梯度下降法)、动量BP算法、学习率可变的最速下降BP算法。

浇头水时间播种期试验分别为6月8日、6月15日、6月25日、7月5日。密度试验均为6月8日。5月16日红花株高达20～30 cm时掐去顶芽，促使分枝增多，增加花蕾数，提高产量。

2.3 编制MATLAB仿真程序

2.3.1 输入样本的确定

根据相关学者[4-6]对侵彻影响因子的分析，确定输入样本向量含有6个因素，即破片的速度，入射角度，长径比，质量，靶厚和形状。为了便于进行BP程序设计，有必要对输入样本向量的因素数据进行处理。

1) 形状因子量化。根据实验的分析，破片头部形状对侵彻的影响大小依次为：锥形>柱形>菱形>球形>方形。因此设：方形=10；球形=20；菱形=30；柱形=40；锥形=50。为了使量化更加接近实际，结合各形状因子对侵彻指标影响的数据分析，用等比例差值法尽量准确地反映各因子的量化表示。此时各形状对指标的影响为：方形=326.17；球形=332.66；菱形=385.55；柱形=416.28；锥形=621.41。结合相应的字母表示，用等比例差值法，固定锥形和柱形之间的差值，最后得到：方形=35.62；球形=35.93；菱形=38.51；柱形=40；锥形=50。

2) 其他因子的输入处理。为使输入样本向量各因素间的差值不致过大，避免对模式识别造成影响，由于速度的单位为m/s，其数值大小在几百到几千之间，所以将速度输入数值缩小100倍，长径比和质量数值都扩大10倍，角度和靶厚数值保持不变。

2.3.2 输出模式的确定

为研究问题的方便，将3种损伤模式分别定为

跳飞：(1 0 0)；嵌入：(0 1 0)；穿透：(0 0 1)。

基于正交试验的设计原则，利用ANSYS/LS-DYNA仿真[7-8]出60组数据，作为训练数据。实体模型及压坑仿真结果如图2所示，部分输入样本及相对应的输出模式如表1所示。

图2 实体模型及压坑仿真结果

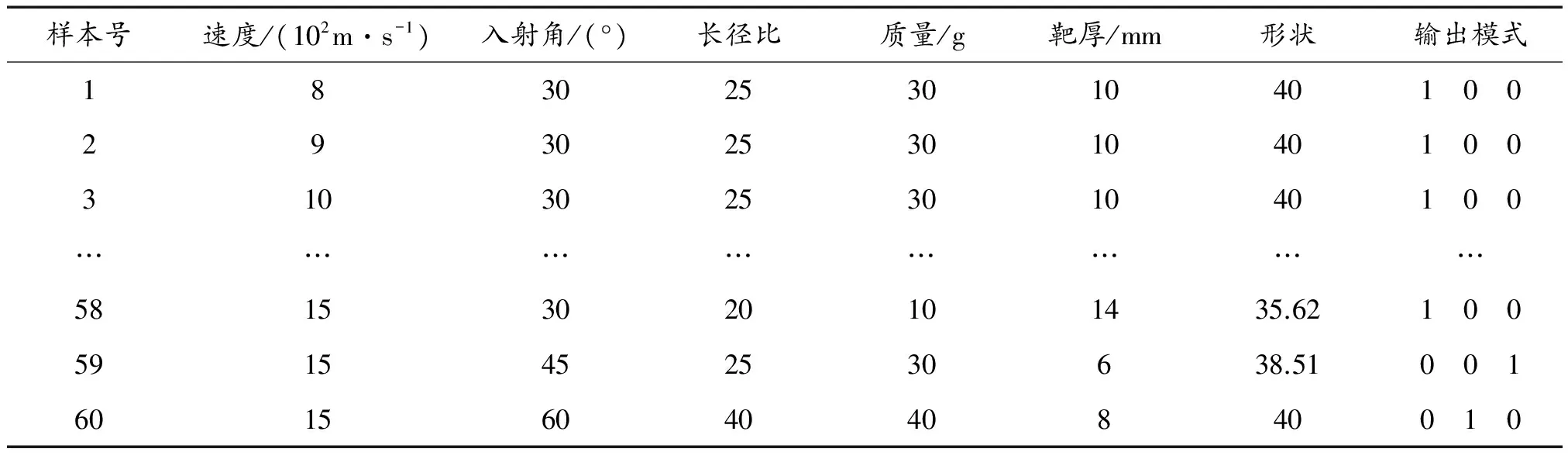
样本号速度/(102m·s-1)入射角/(°)长径比质量/g靶厚/mm形状输出模式1830253010401 0 02930253010401 0 031030253010401 0 0……………………58153020101435．621 0 05915452530638．510 0 160156040408400 1 0

2.3.3 建立BP网络所需参数的确定

拟建立两层的BP网络，其相关参数的确定如下：

1) 隐层神经元的个数

对于用于模式识别/分类的BP网络，根据前人经验，可以参照以下公式设计

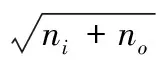
(1)

式中：n为隐层神经元个数；ni为输入样本神经元数，即输入样本元素数；n0为输出神经元数，即输出样本元素数；a为从1到10之间的数。将ni=6，n0=3代入式(1)，取a=2，确定隐层神经元个数n=5。

2) 激活函数的选取

根据一般的程序默认，第一层选择S形函数logsig，第二层选择线性函数purelin。传输函数的选取主要取决于输出，建网程序设置输出在0和1之间，所以第一层和第二层的传输函数都可选择为对数S形函数。因此本研究将对选取不同的传输函数的训练情况进行对比，以确定最佳的满足性能要求的传输函数选取。

3) 训练方法及参数的选择

采用不同的训练方法对网络进行训练，各训练方法选取默认初始学习率为0.01，训练次数为20 000次，期望误差为0.001。

网络的初始化权值和阈值的随机选取，所以每次运行程序结果将不相同，反复运行，直到满意为止。

2.3.4 编制MATLAB仿真程序

在所建立的BP网络中，共需要用到两个传输函数的选取，因为目标输出是得到0和1之间的数，为尽可能地避免出现负值，输入层和输出层的传输函数都不选用正切S形函数。为使加权和尽快收敛输入层选择对数S形函数，输出层可分别选对数S形或线性传输函数。网络的训练选用上述常用的traingd，traingdm，traingda和traingdx函数[9]。共分为8种情况，如表2所示。

对以上8种情况分别建立网络，对网络进行训练，训练次数为 20 000次，误差性能指标为0.001，其他网络参数均用Matlab中的默认值，由于BP网络每次训练初始化权值和阈值都取随机值，故同一程序每次训练所得的误差性能值都不同，所以每种情况训练的次数为30次，选取最小的误差性能值的情况汇总如图3(a)～图3(h)所示(图的纵坐标为误差性能，横坐标为训练次数)。将训练情况汇总表格(见表2)，由列表情况可知，在其他情况相同的条件下，输出层传输函数采用purelin函数要比采用logsig函数的各训练函数的最小误差性能徝更接近于误差性能指标，从表2可以看出，除traingdm函数略有差异外，其他均属上述情况，所以最终的MATLAB程序选用上述的第4种情况建立。

表2 训练情况汇总

2.4 仿真结果及验证

将60个输入样本输入由上述第4种情况创建的BP网络中进行计算，得到的仿真结果汇总如表3。从表3可看出，经过网络训练，仿真所得到的各种输出模式结果进行取整运算后，与实际的期望输出相吻合，输入样本都满足输出模式的要求。虽然网络误差性能值没达到所要求的0.001，但用作模式识别已经在允许的误差范围内。改变输入因子的值，取3个不同于训练样本的其他样本进行验证，验证试验号为61*、62*、63*，验证样本的输入因子及仿真输出和期望输出如表4所示(表中的单位和表1相同)。

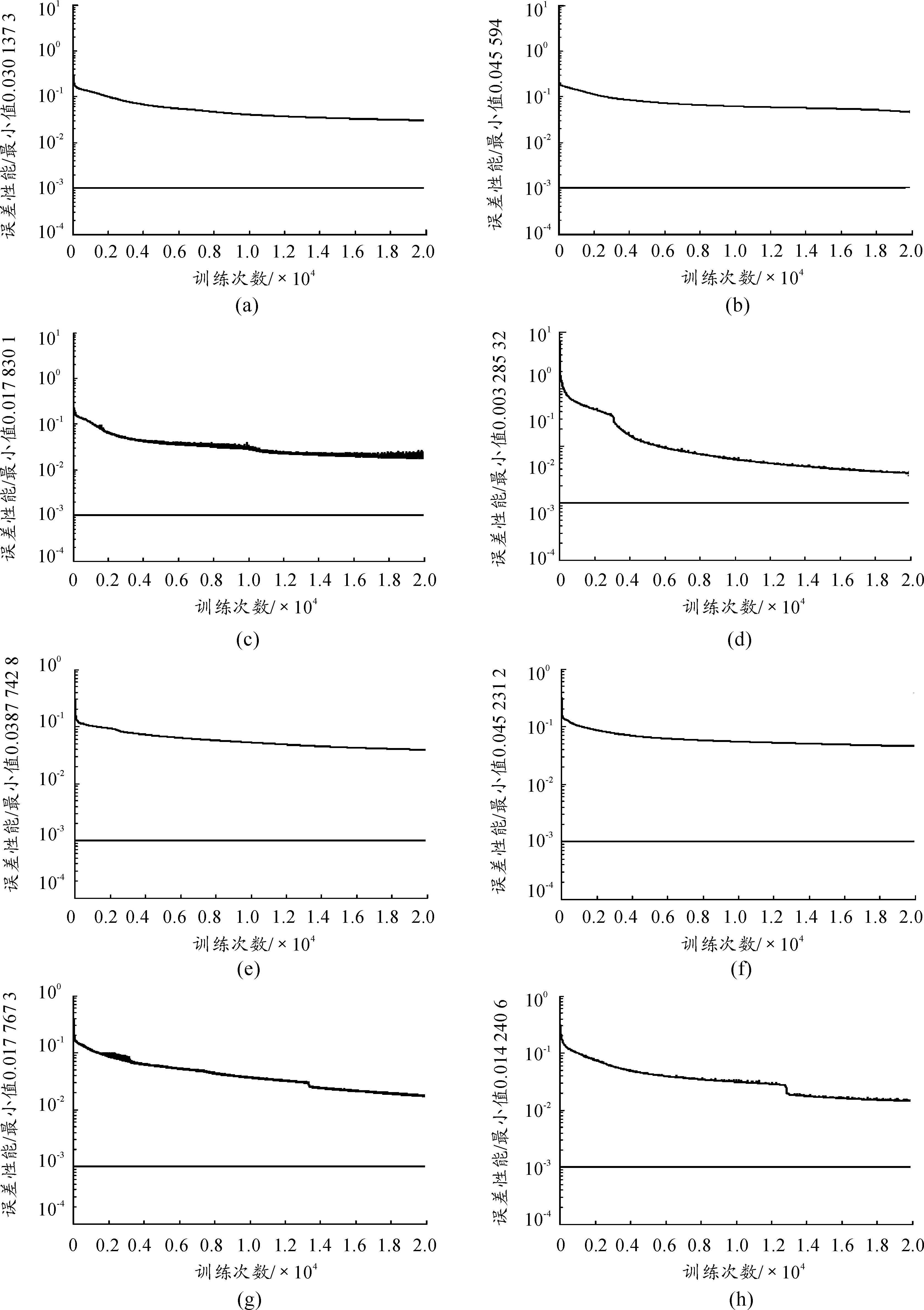
图3 各训练的误差性能曲线

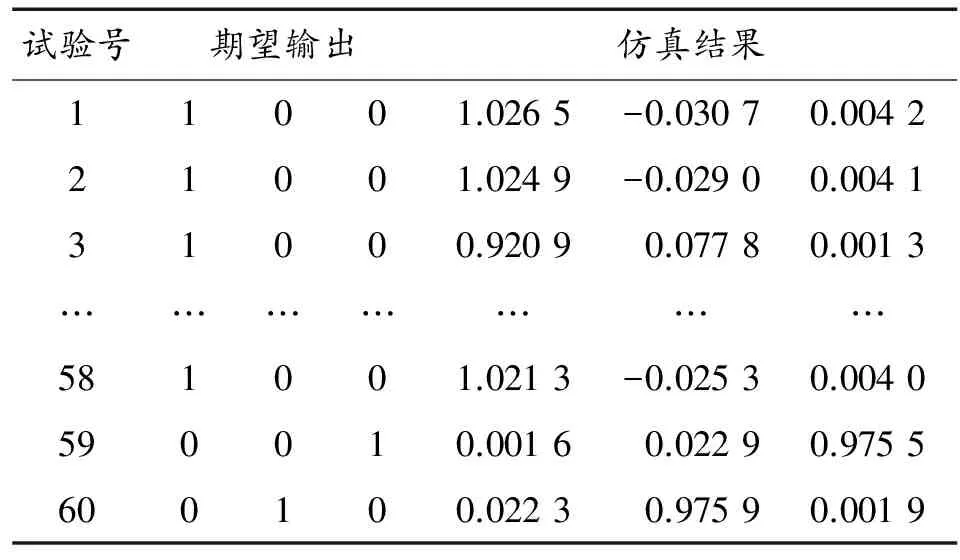
试验号期望输出仿真结果11001．0265-0．03070．004221001．0249-0．02900．004131000．92090．07780．0013…………………581001．0213-0．02530．0040590010．00160．02290．9755600100．02230．97590．0019

上述仿真结果表明，用神经网络进行侵彻损伤模式识别是可行的，在误差允许的范围内，仿真的结果可用来对不同的输入样本进行侵彻损伤模式的预测与识别。

3 结论

本文运用MATLAB中的神经网络工具箱，进行BP网络设计，基于正交试验设计原则，利用ANSYS/LS-DYNA仿真出60组不同条件小的弹丸侵彻靶板模式，作为试验样本数据处理后输入仿真程序进行训练。通过对比采用不同的传输函数和训练算法得到的网络误差性能值，最终选定输出层为purelin函数，网络采用traingdx算法的两层BP网络进行样本的仿真模拟，其误差精度达到了 0.003 29，满足试验要求。经过验证，网络的输出模式与实际输出相符，证明采用神经网络进行侵彻损伤的模式识别是可行的。

表4 验证样本输入及输出

[1] 张世臣,米双山.LY-12靶板在爆炸冲击波作用下损伤的有限元分析[J].兵工自动化,2008,27(5):18-19.

[2] 蒋宗礼.人工神经网络导论[M].北京：高等教育出版社，2003.

[3] 高隽.人工神经网络原理及仿真实例[M].北京：机械工业出版社，2003.

[4] 尹峰，张亚栋.常规武器爆炸产生的破片及其破坏效应[J].解放军理工大学学报(自然科学版)，2005.

[5] 张国伟，徐立新.终点效应与靶场试验[M].北京：北京理工大学出版社，2009.

[6] 闻新，周露，李翔,等.MATLAB神经网络仿真与应用[M].北京：科学出版社，2003.

[7] 陈健，米双山，张锡恩.基于LS-DYNA球形破片穿甲的网格划分研究[J].弹箭与制导学报，2005,25(2):51-55.

[8] 时党勇，李裕春，张胜民.基于ANSYS/LS-DYNA8.1进行显式动力分析[M].北京：清华大学出版社，2005.

[9] 周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社，2005.

PenetrationPatternRecognitionBasedonArtificialNeuralNetwork

WANG Shuo, SHI Quan

(Department of Equipment Command and Management, Ordnance Engineering College, Shijiazhuang 050003, China)

In order to study the specific pattern of fragmentation penetrating the target plate under the influence of multi factors, this paper uses the artificial neural network method to identify the input parameters and obtains the corresponding target damage model. Based on the principle of orthogonal experimental design, this paper uses ANSYS/LS-DYNA to simulate the model data of 60 sets of fragments penetrating into the target plate, and trains the neural network as the input data of neural network training. In addition, three sets of data are selected as the validation data to verify the training effect of the neural network. The results show that the artificial neural network can effectively identify the specific damage patterns of fragments to target plates under multi factors.

artificial neural network; penetration model; finite element simulation; pattern recognition

2017-05-25；

2017-06-15

王烁(1993—),男,硕士研究生，主要从事装备战场损伤理论与技术研究; 石全(1966—),男,教授，博士生导师，主要从事装备战场损伤理论与技术研究。

10.11809/scbgxb2017.10.013

本文引用格式：王烁，石全.基于人工神经网络的侵彻毁伤模式识别[J].兵器装备工程学报，2017(10):60-64.

formatWANG Shuo, SHI Quan.Penetration Pattern Recognition Based on Artificial Neural Network[J].Journal of Ordnance Equipment Engineering,2017(10):60-64.

E92

A

2096-2304(2017)10-0060-05

(责任编辑周江川)