30 mm小口径炮弹发射时炸药装药应变率及过载安全性分析

王小峰，陶 钢，丁贵鹏，赵爱德，范 强，刘 龙

(1.南京理工大学 能源与动力工程学院， 南京 210094； 2.九江精密测试技术研究所， 江西 九江 332000； 3.重庆长安工业(集团)有限责任公司， 重庆 401120)

【装备理论与装备技术】

30mm小口径炮弹发射时炸药装药应变率及过载安全性分析

王小峰1，陶 钢1，丁贵鹏1，赵爱德2，范 强3，刘 龙3

(1.南京理工大学 能源与动力工程学院， 南京 210094； 2.九江精密测试技术研究所， 江西 九江 332000； 3.重庆长安工业(集团)有限责任公司， 重庆 401120)

采用有限元LS-DYNA软件对30 mm小口径炮弹发射过程进行数值模拟，分析了不同时刻弹丸等效应变的分布规律，分别计算了炸药装药应力波作用阶段和装药整体过载作用阶段炸药装药的等效应变、应变率，讨论了不同弹底厚度对炸药装药最大等效应变及应变率的影响。弹底厚度为3.5 mm、2.5 mm和2 mm时，炸药装药等效应变、应变率随时间变化趋势一致；当弹底厚度由3.5 mm减小至2 mm，装药最大等效应变由4.42%增加到6.23%，最大等效应变率由167.64 s-1增加到277.91 s-1；且弹底厚度越薄(特别是弹底厚度减小到2 mm时)，炸药装药加载应力越大，炸药装药的等效应变、应变率越大。本文采用非均质炸药起爆判据，当弹底厚度为3.5 mm、2.5 mm时，炸药装药发射安全，当弹底厚度减小至2 mm时，炸药装药发射不安全。

小口径炮弹；炸药装药；数值模拟；过载分析；等效应变；等效应变率；弹底厚度；发射安全性

弹丸在膛内发射时受到强烈的冲击载荷，当冲击载荷超过弹体内炸药的承受能力时，可直接激发炸药而导致膛炸[1]。因此，对于炸药装药的发射过载、冲击起爆性能分析很有必要。

图1是某型号30 mm小口径炮弹，是一种高爆双用途弹丸炸药，预期典型目标是打击轻装甲车。该弹丸炸药装药是一种PBX炸药。PBX是高聚物粘结炸药(Polymer Bonded Explosive)的简称，是由主体炸药(如RDX、HMX、TATB等)和高聚物粘结剂等组成的固体高能炸药，它是弹药的主要装药。

图1 某型号30 mm小口径炮弹

发射载荷下，炸药装药是最薄弱的承力环节，在外界力-热环境下炸药装药的力学性能决定了炸药构件的易损性和形稳性，也影响炸药的过载安全性和可靠性[2]。为了确保弹药服役时的安全性，必须研究炸药装药在动态加载条件下的力学性能及本构关系。张奇[3]根据装药过载的力学特征，提出了发射过载的两个阶段，应力波作用阶段和装药整体过载作用阶段。在前一阶段，炸药装药的应变率和变形能是装药安全发射的主要影响因素，后一阶段，装药的过载应力是主要因素。文献[4]也提出，通过观测炸药装药在冲击压缩作用下炸药的内部应力、应变、应变率、应力率等力学参数变化规律以及反应程度，从而研究炸药装药在撞击压缩状态下的安全性及点火机理。

研究发现[2-3,5]，炸药装药的动态力学性能对应变率比较敏感。如Blumenthal[6]通过动态试验(霍普金森压杆)研究了不同应变率下(10-3～2 000 s-1)PBXN-110和以HTPB为基的粘结剂的压缩性能，发现高应变率条件下，应变率对PBX炸药的压缩应力峰值影响很大。吴会名[7]通过试验发现，在高应变率条件下，PBX炸药的弹性模量、压缩强度随着应变率的增加呈非线性关系增加；陈荣[8]研究了一种PBX炸药试样在复杂应力动态加载下的力学性能，试验加载涵盖了从10-4～103s-1的应变率范围，发现该试样的压缩强度随应变率的增加而增加。

本文采用ANSYS/LS-DYNA结构分析非线性有限元软件对弹丸膛内发射过程进行数值模拟，分析了不同时刻弹丸等效应变的分布规律，分别计算了应力波作用阶段和装药整体过载作用阶段炸药装药的等效应变、应变率，引入冲击起爆理论判据分析了炸药装药发射过载安全性，为小口径弹丸结构优化设计及炸药装药过载安全性分析评估提供了参考。

1 计算模型及参数

用SolidWorks软件建立30 mm炮弹三维实体模型，如图2所示，由模拟引信(内部构造省略，质量与真实引信相同)、弹体(弹底厚度为3.5 mm)、炸药装药、药型罩4部分组成。

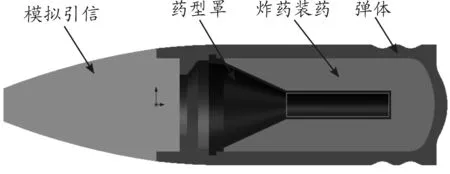
图2 某型号30 mm小口径炮弹三维实体模型

将实体模型导入HyperMesh进行网格划分。图3是弹丸网格模型，全部采用六面体网格单元，弹丸各部分内共 122 900个节点。计算的物理模型为轴对称模型，为了更好地提高计算效率，取模型的1/4进行计算。

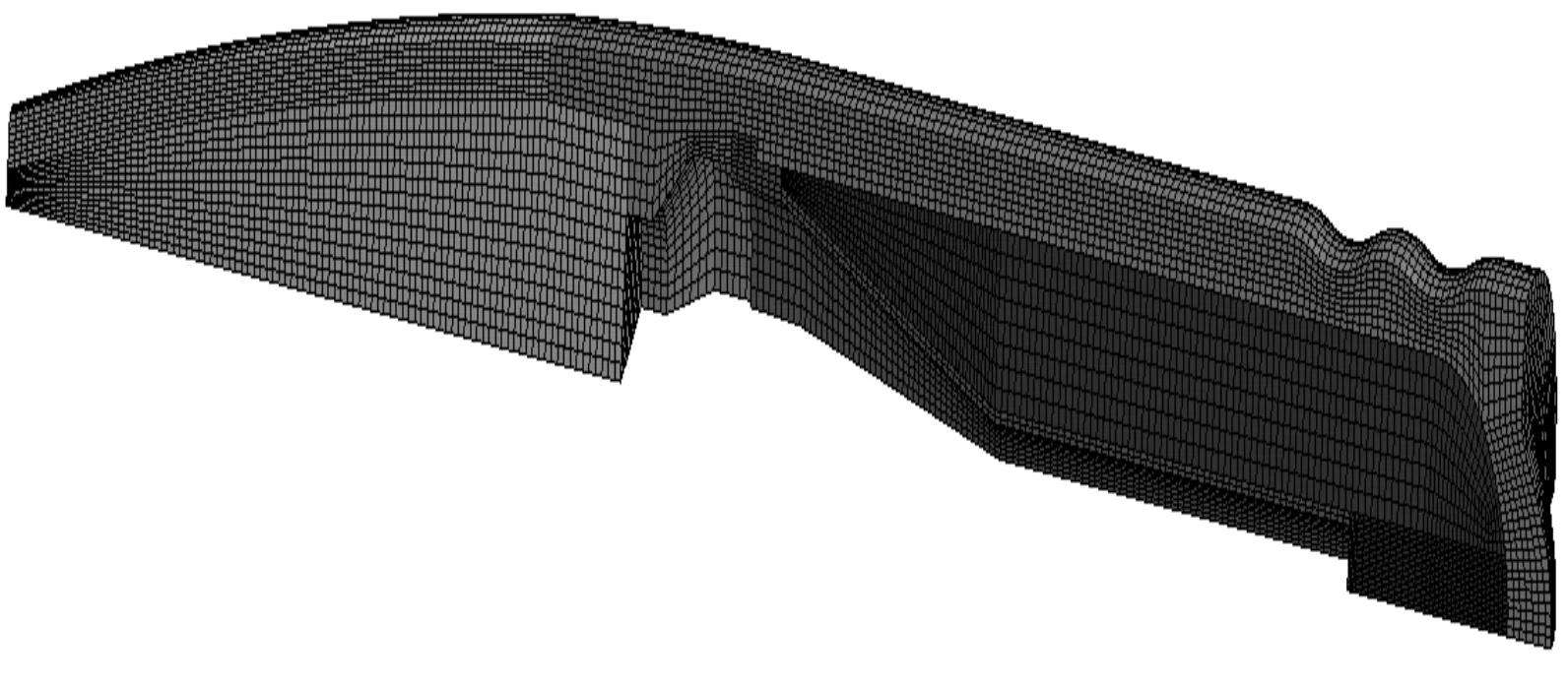
图3 弹丸网格模型

再将实体模型转换为有限元模型后，生成k文件并在LS-PREPOST里完成k文件的编辑，利用ANSYS/LS-DYNA3D进行求解分析[9-10]。步骤如下[11]：

1) 定义单元类型、材料参数[7,12-14]和状态方程。弹体选用823钢，药型罩选用紫铜，均采用JOHNSON_COOK模型和Gruneisen状态方程；模拟引信采用弹性材料模型；内部装药选用PBX-9404炸药(HMX94%，硝化纤维3%，三氯代乙基磷酸酯3%)，采用分段线性塑性模型。材料的主要参数如表1、2所示，表中A、B、n、c、m为材料常数。

表1 弹体、药型罩材料参数

表2 引信、炸药装药材料参数

2) 生成PART，定义接触，采用Automatic_Surface_to_Surface自动面面接触，设置边界约束条件，使用*BOUDARY_SPC_SET对弹丸轴对称面进行约束；

3) 定义弹底压缩应力—时间曲线。编写内弹道程序，得到该型号30 mm小口径炮弹弹底压缩应力曲线，如图4所示，在弹底施加压力载荷；

4) 设置求解相关控制参数、输出控制设定并生成和完善LS-DYNA输入数据文件(关键字文件)；将数据输入文件递交给LS-DYNA求解器进行计算；应用LS-DYNA后处理进行结果分析。

图4 弹底压缩应力随时间变化曲线

2 数值计算结果及分析

2.1 弹丸等效应变云图

用后处理软件LS-PREPOST分析数值计算结果。图5是弹丸(弹底厚度为3.5 mm)典型时刻等效应变(effective strain)云图。

由图5可知，弹丸的应变主要集中在炸药装药，且随着装药高度的增加而减小，在装药尾部区域变形最大，有应力集中现象。0.2 ms时弹丸最大等效应变为1.30%，随着弹底压缩应力的增加，弹丸等效应变增大，在0.45 ms时刻弹丸等效应变达到最大值4.42%，然后随着弹底压缩应力降低，弹丸等效应变减小。

图5 弹丸典型时刻等效应变云图

2.2 炸药装药应变率分析

炸药装药在0.45 ms时达到最大应变，确定最大应变单元为H86936，如图6所示，作出该单元等效应变随时间变化曲线，对其取一阶导数，可以得到等效应变率随时间变化曲线，如图7所示(弹底厚度为3.5 mm)。

由图6可知，炸药装药等效应变在0.45 ms时达到最大值4.42%，然后随着弹丸在膛内的运动，等效应变缓慢减小，2.1 ms以后炸药装药等效应变保持在2.30%左右。

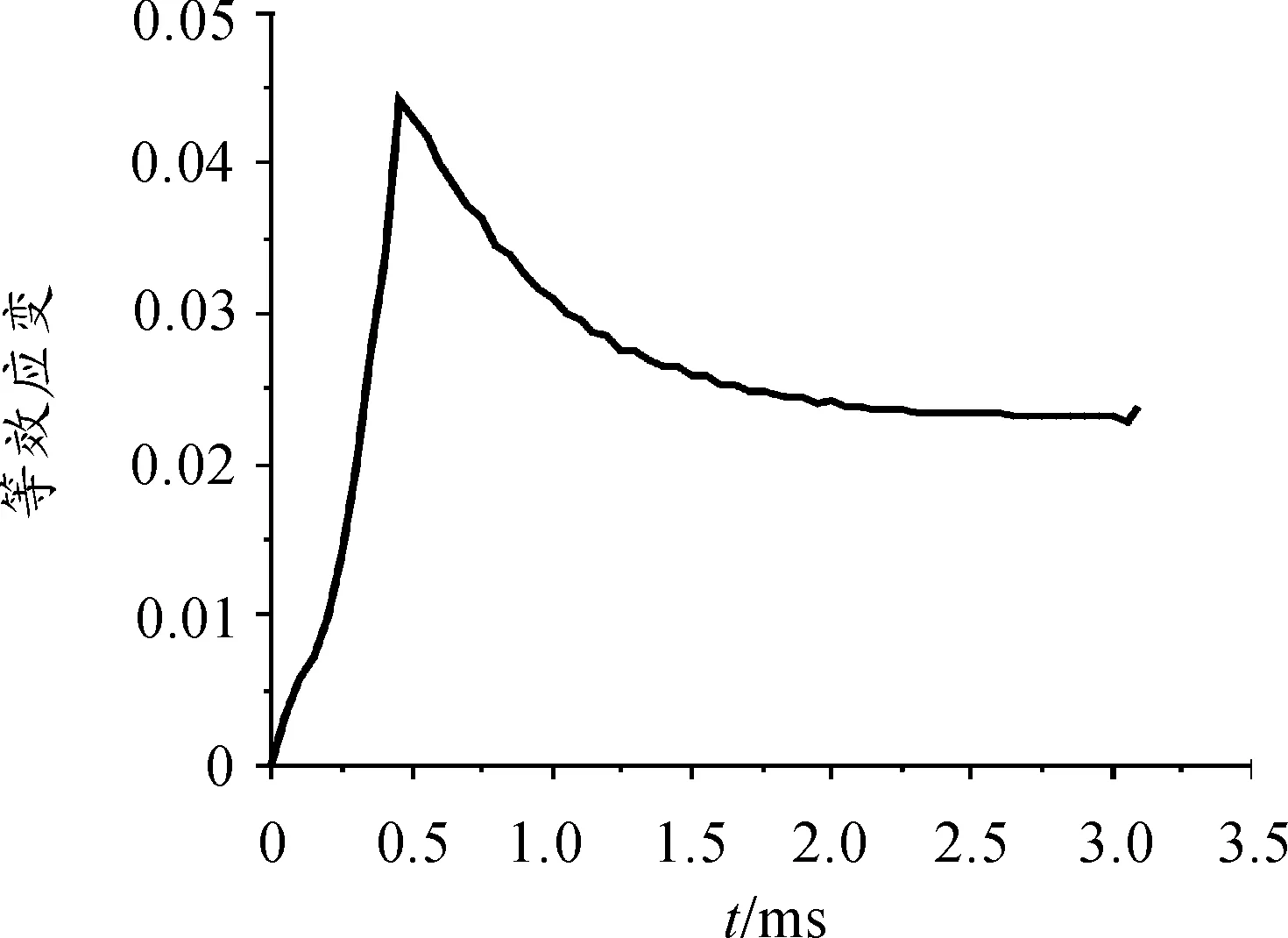
图6 装药等效应变-时间曲线

图7 装药等效应变率-时间曲线

对比图6、图7可以发现，发射初始时刻，弹丸受到火药燃气的推动，炸药装药接触弹底以后，在装药内部产生应力波，应力波由底部向顶部传播，炸药装药应变虽然为零，但等效应变率非零，达到65.50 s-1，开始时炸药装药所受应力小于其屈服极限，应力波为弹性波[15]，即波阵面后方炸药装药发生弹性变形；0.1 ms时炸药装药等效应变增加到0.58%，等效应变率降低到39.85 s-1，即在发射初期0～0.1 ms时间段内，炸药装药随着弹性应变的增大越不容易变形；0.1 ms时刻以后，随着药筒发射药继续燃烧，弹底所受压缩应力增大，炸药装药所受应力超过其屈服极限，装药出现塑性变形，应力波不仅有弹性波，还有塑性波，炸药装药等效应变、应变率急剧增大；0.40 ms时炸药装药等效应变率增大到最大，为167.64 s-1，然后降低，而炸药装药等效应变继续增大；0.45 ms时炸药装药等效应变增大到最大，为4.42%，等效应变率减小到92.36 s-1，说明在0.40～0.45 ms时间段弹底所受压缩应力继续增大，但增速放缓，0.45 ms时弹底所受压缩应力达到最大。0～0.45 ms时间段即是应力波作用阶段，在该阶段，炸药装药等效应变、应变率达到最大，是分析装药安全性的主要因素。

0.45 ms时刻以后，弹底所受火药燃气压缩应力降低，炸药装药处于弹性卸载段，炸药装药等效应变减小，等效应变率为负值，其绝对值减小直到趋于零，到2.1 ms时炸药装药等效应变减小到2.39%，等效应变率增大到-1.06 s-1，总应变弹性部分的应变得到恢复，塑性应变被保留下来；从2.1～3.1 ms(出炮口)时间段，炸药装药等效应变保持在2.30%左右，等效应变率接近零。0.45～3.1 ms(出炮口)时间段即是装药整体过载作用阶段，在该阶段，炸药装药等效应变、应变率不是影响装药发射安全性的主要因素，而应力与其作用时间成为主要因素。

分析结果与文献[3]提出的发射过载的两个阶段一致。

2.3 不同弹底厚度对炸药装药应变率的影响

前面计算时弹底厚度为3.5 mm，为了得到不同弹底厚度对装药应变率的影响，基于LS-DYNA软件模拟弹底厚度为2.5 mm、2 mm时30 mm小口径弹丸膛内发射过程，除弹底厚度外，其余参数保持不变。

不同弹底厚度时炸药装药最大应力单元号分别为H86936(弹底厚度3.5 mm)、H487382(弹底厚度2.5 mm)与H529115(弹底厚度2 mm)，运用后处理软件LS-PREPOST及作图软件作出不同弹底厚度时炸药装药最大应力单元等效应力—时间曲线，如图8所示。

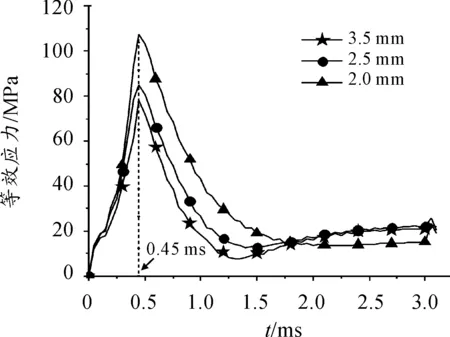
图8 不同弹底厚度时装药等效应力-时间曲线

由图8可知，随着弹底厚度由3.5 mm减小至2 mm，炸药装药最大等效应力增大，弹底厚度为3.5 mm时，炸药装药最大等效应力为78.34 MPa，同理2.5 mm时装药最大等效应力为85.21 MPa，2 mm时装药最大等效应力为107.40 MPa。从发射初始时刻到最大应力时刻的时间段都相同(0～0.45 ms)，说明弹底厚度越薄(特别是弹底厚度减小到2 mm时)，炸药装药加载应力率越大。

如图9所示，作出最大应力时刻(0.45 ms)不同弹底厚度时炸药装药等效应变(effective strain)云图。

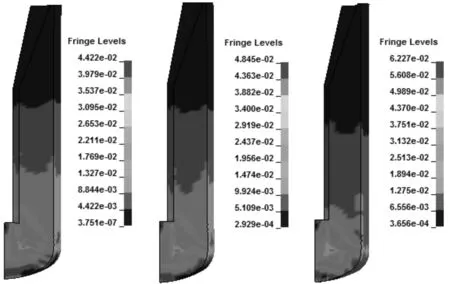
图9 不同弹底厚度时(左→右，3.5 mm、2.5 mm、2 mm) 装药等效应变云图(单位 Mbar)

由图9可知，在最大应力时刻(0.45 ms)，随着弹底厚度减小，炸药装药最大等效应变增大，由4.42%(弹底厚度3.5 mm)增大到4.85%(弹底厚度2.5 mm)，再继续增大到6.23%(弹底厚度2 mm)。可以发现，在弹底厚度由2.5 mm减小至2 mm的过程中，最大等效应变增长较快。

根据等效应变云图，确定最大应变单元，单元号为H487382(弹底厚度2.5 mm)与H529115(弹底厚度2 mm)，如图10所示，作出等效应变—时间曲线，然后求一阶导数得到等效应变率—时间曲线，如图11所示。

图10 不同弹底厚度时装药等效应变—时间曲线

由图10可知，当弹底厚度减小至2.5 mm、2 mm，炸药装药等效应变随时间变化趋势与弹底厚度为3.5 mm时一致。从2.1～3.1 ms(出炮口)时间段，弹底厚度为2 mm时，炸药装药最大应变单元的等效应变保持在4.20%左右，弹底厚度为2.5 mm时，该值保持在3.00%左右。在弹底厚度从3.5 mm减小至2.5 mm的过程中，炸药装药等效应变增长较慢，弹底厚度从2.5 mm减小至2 mm的过程中，等效应变增长较快。

图11与图7相比较可发现，当弹底厚度减小至2.5 mm、2 mm，炸药装药等效应变率随时间变化趋势与弹底厚度为3.5 mm时一致。发射初始时刻，弹底厚度为2.5 mm时，炸药装药最大应变单元的等效应变率为73.77 s-1，弹底厚度为2 mm时该值85.91s-1；0.1 ms时，炸药装药等效应变率分别降低到50.60 s-1(弹底厚度2.5 mm)、45.91s-1(弹底厚度2 mm)，炸药装药等效应变分别增大到0.66%(弹底厚度2.5 mm)、0.69%(弹底厚度2 mm)，这与弹底厚度为3.5 mm时，炸药装药初始时刻的等效应变率65.50 s-1和0.1 ms时的等效应变率39.85 s-1、等效应变0.58%数值大小相近。说明在弹丸发射的0～0.1 ms时间段，不同弹底厚度对应的炸药装药发生弹性变形时，装药的等效应变、应变率没有发生太大变化。

弹底厚度为2.5 mm时，最大应变单元(H487382)在0.35 ms时刻应变率达到最大，为201.51 s-1；弹底厚度为2 mm时，最大应变单元(H529115)在0.35 ms时刻应变率达到最大，为277.91 s-1。弹底厚度减小时，炸药装药最大应变单元的最大等效应变率增加，且在弹底厚度由2.5 mm减小至2 mm的过程中，应变率增长较快。从图8可知，弹底厚度减小时，炸药装药加载应力率增大，因此，炸药装药的等效应变、应变率随应力率的增加而增大。这也与文献[4]的结论相一致，应力上升速率对PBX炸药颗粒的变形速率有直接的影响。

3 炸药装药发射安全性分析

由上节分析可知，在炸药装药发射过载应力波作用阶段等效应变、等效应变率是影响装药安全性的主要因素，但在不同的发射载荷、环境下，还不能准确确定临界破坏应变、临界破坏应变率值。已有的安全性理论都是适用于整个发射过载阶段。针对不同PBX炸药装药在应力波作用阶段的过载安全性的准确分析还在发展之中。

现代武器系统中的炸药一般为非均质炸药，即炸药在浇铸、压装，结晶过程中所引起的密度不连续，如存在气泡、空穴、杂质等。对这类炸药的冲击起爆，热理论认为在机械作用下(尤其是在冲击之下)，开始主要是局部区域的炸药受到加热，即在炸药中产生热点[16]，随之的热分解导致快速放热反应。产生热点的原因通常认为是装药结构的不均匀性。

对热点应用的热平衡方程为：

(1)

式中：cp、ρ、λ分别为炸药的定压比热容、密度和导热系数，t为时间，Q为热源，k0为指数前因子，R为气体常数，E为活化能，T为热力学温度。

如果炸药内反应产生的能量恰恰和从它表面传走的热量相等，即炸药温度增加的速度等于零，可得到临界值δc：

(2)

式中ε为t=0～t0时间内输入热点的能量，a2=λ/ρcp。

文献[14]作出几种常用炸药受到冲击波后温度和冲击压应力的关系图，发现在一定压应力范围内，近似为线性关系，若炸药的初始温度为T1，压应力为零，则

T-T1=βp

(3)

式中：对某种炸药来说，β对应一个常数。

可得到冲击波后进入炸药的热能为：

ε0=cp(T-T1)t0D=βcppt0D

(4)

式中：t0为飞板中冲击波来回传播的时间，D为炸药内冲击波速度。

若以ε作为瞬时输入炸药的热能，代入式(2)，则可得到：

(5)

因为只有P、D、t0为变量，所以炸药临界起爆能量判据公式为[14]：

p2D2t=const

(6)

式中：p为作用于炸药的压缩应力，t是冲击载荷时间。

假设炸药受到平面一维冲击波加载。

通过对各种炸药的大量计算，在一定压缩应力范围内，当p变化达5～6倍时，D的变化不到20%，所以一般认为当p变化不大时，D是常值。这样就得到著名的非均质炸药的起爆判据[17]：

p2t=const

(7)

文献[17]利用能量守恒定律证明了用飞片冲击非均相炸药的上述引爆判据。认为p2t的概念隐含着输入单位体积炸药内的能量达到某一临界值时，炸药即起爆。即炸药的起爆必须先给予一定的能量，这个能量的最小值称为临界起爆能量。

根据文献[14]的试验数据，炸药PBX-9404(密度1.84 g/cm3，含HMX94%，硝化纤维3%，三氯代乙基磷酸酯3%)的临界起爆条件为p2t=4.7×1012Pa2·s。

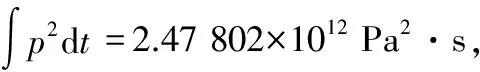
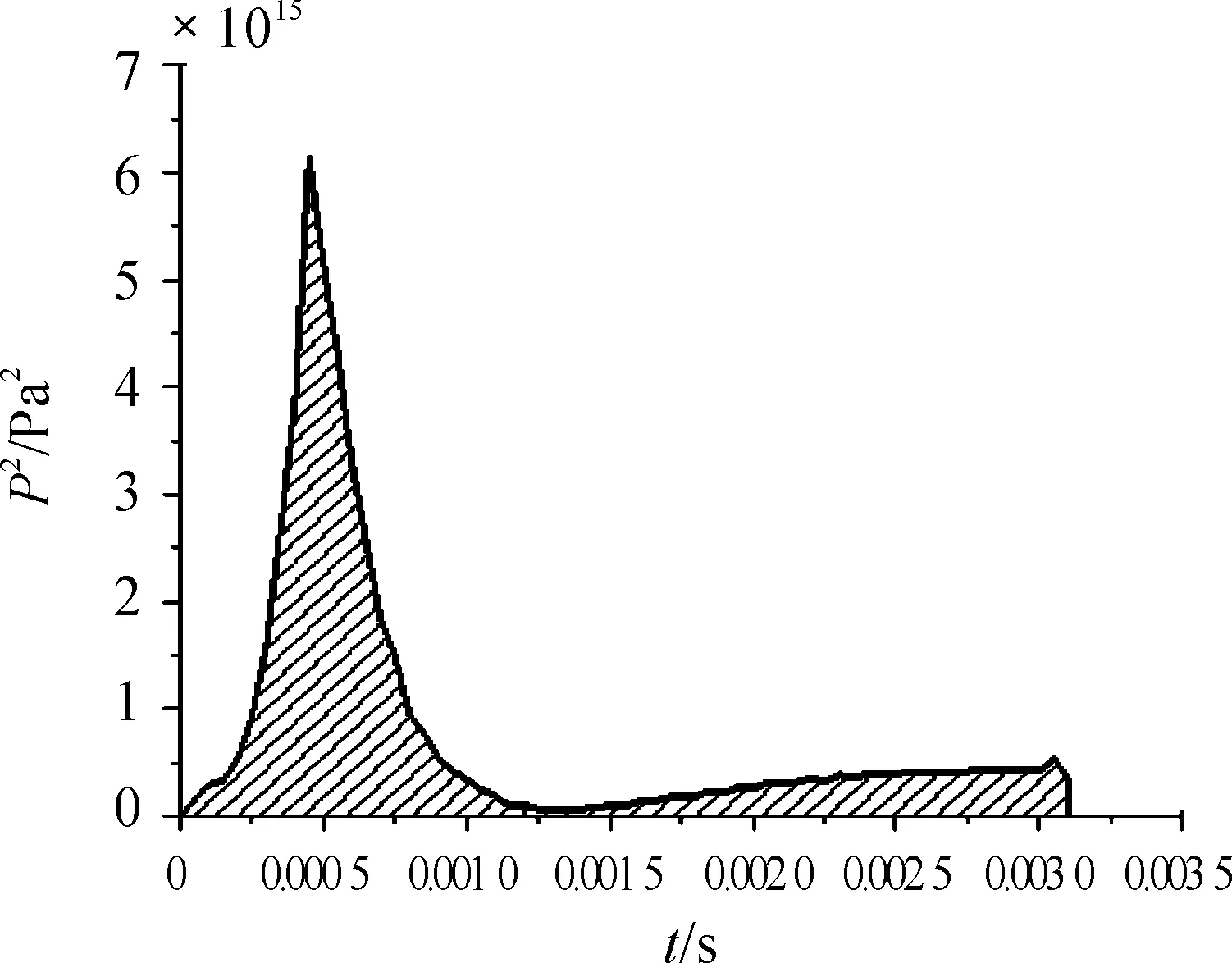
图12 装药最大应力单元p2-t曲线(弹底厚3.5 mm)

4 结论

1) 弹丸发射时，弹丸的应变主要集中在炸药装药，随着装药高度的增加等效应变减小，在装药尾部区域变形最大，有应力集中现象，等效应变先上升后降低，在0.45 ms时刻弹丸最大等效应变达到最大值4.42%(弹底厚度为3.5 mm)。

2) 发射载荷下(弹底厚度为3.5 mm)，0～0.45 ms时间段是应力波作用阶段，其中0～0.1 ms时间段内，应力波为弹性波，炸药装药等效应变率随等效应变的增加而降低，0.1 ms时刻以后，应力波不仅有弹性波，还有塑性波，炸药装药等效应变、应变率急剧增大，在0.40 ms时刻弹丸最大等效应变率达到最大值167.64 s-1，等效应变、应变率是分析装药过载安全性的主要因素；0.45～3.1 ms(出炮口)时间段是装药整体过载作用阶段，炸药装药等效应变趋于定值2.30%，等效应变率趋于零，应力与其作用时间为主要因素。

3) 当弹底厚度减小至2.5 mm、2 mm时，炸药装药等效应变、应变率随时间变化趋势与弹底厚度为3.5 mm时一致；弹底厚度由3.5 mm减小至2 mm，装药最大等效应变由4.42%增加到6.23%，最大等效应变率由167.64 s-1增加到277.91 s-1，且在弹底厚度由2.5 mm减小至2 mm的过程中，装药最大等效应变与应变率增长较快。弹底厚度越薄(特别是弹底厚度减小到2 mm时)，炸药装药加载应力率越大，炸药装药的等效应变、应变率越大。

4) 本文采用非均质炸药起爆判据，积分计算后发现，当弹底厚度为3.5 mm、2.5 mm时，炸药装药发射安全，而弹底厚度为2 mm时，炸药装药发射不安全，炸药装药受弹底载荷冲击起爆的概率较大，设计弹丸时应高度注意。

[1] 金志明,翁春生,张国强.膛炸模式及其机理分析[J].兵工学报,2001,22(4):448-451.

[2] 李尚昆,黄西成,王鹏飞.高聚物黏结炸药的力学性能研究进展[J].火炸药学报,2016,39(4):1-11.

[3] 张奇,闫华,白春华.装药发射过载动力学研究[J].振动与冲击,2003,22(2):78-80.

[4] 屈可朋,沈飞,王世英,等.RDX基PBX炸药在不同应力率下的撞击安全性[J].火炸药学报,2014(6):40-43.

[5] 李亮亮,沈飞,屈可朋,等.炸药装药在不同应变率响应条件下的安全性研究进展[J].火炸药学报,2016,39(1):14-22.

[6] BLUMENTHAL W R,THOMPSON D G,CADY C M.et a1.Compressive properties of PBXN-110 and its HTPB based binder as a function of temperature and strain rate[C]//Proceedings of the 12th International Detonation Symposium.Washington,DC:Office of Naval Research.2002:530-549.

[7] 吴会民.几种含能材料本构关系研究[D].长沙：国防科学技术大学,2003.

[8] 陈荣.一种PBX炸药试样在复杂应力动态加载下的力学性能实验研究[D].长沙：国防科学技术大学,2010.

[9] 时党勇.基于ANSYS/LS-DYNA 8.1进行显式动力分析[M].北京：清华大学出版社,2005.

[10] 白金泽.LS-DYNA3D理论基础与实例分析[M].北京：科学出版社,2005.

[11] 刘永刚,沈培辉,岳永丰,等.薄壁榴弹的发射强度计算与仿真分析[J].机械制造与自动化,2014(3):122-125.

[12] 王豪.发射载荷下炸药装药密度对炸药应力和温度的影响[J].四川兵工学报,2011,32(3):28-31.

[13] 赵梓君,毕世华,向超文,火炮发射过程中装药响应数值模拟研究[J].北京理工大学学报,2014.

[14] 章冠人,陈大年.凝聚炸药起爆动力学[M].北京：国防工业出版社,1991.

[15] 郭伟国.应力波基础简明教程[M].西安：西北工业大学出版社,2007.

[16] 奥尔连科.爆炸物理学[M].北京：科学出版社,2011.

[17] WALKER F E，WASLEY R J.Critical energy for shock initiation of heterogeneous explosives[C].7th Symposium on Detonation，WhiteOak，1982：294-302.

AnalysisofStrainRateandOver-LoadingSafetyofExplosiveChargewhen30mmSmall-CaliberShellareFired

WANG Xiaofeng1, TAO Gang1, DING Guipeng1, ZHAO Aide2, FAN Qiang3, LIU Long3

(1.School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2.Jiujiang Precision Measuring Technology Research Institute, Jiujiang 332000, China; 3.Chongqing Chang’an Industry (Group) Limited Liability Company, Chongqing 401120, China)

The finite element LS-DYNA software was used to simulate the launch process of 30 mm small-caliber shell. The distribution of the effective strain were analyzed at different moments. The equivalent strain, strain rate of the explosive charge are calculated respectively in the stage of the stress wave and the charge whole overload. The effect of different thickness on the maximum equivalent strain and strain rate of explosive charge were discussed. When the bottom thickness is 3.5 mm, 2.5 mm and 2 mm, the equivalent strain, strain rate of the explosive charge is consistent with the time trend. With the bottom thickness from 3.5 mm to 2 mm, the maximum equivalent strain of the charge increased from 4.42% to 6.23% and the maximum equivalent strain rate increased from 167.64 s-1to 277.91 s-1. When the thickness of the bottom is thin (especially when the thickness of the bottom is reduced to 2 mm), the greater the loading stress rate of the explosive charge, the greater the equivalent strain, strain rate of the explosive charge. In this paper, heterogeneous explosives initiation criteria is used. It is obtained that when the bottom thickness is 3.5 mm, 2.5 mm, the explosive charge is safe. When the bottom thickness is reduced to 2 mm, the explosive charge is unsafe.

small-caliber shell; explosive charge; numerical simulation; over-loading analysis; effective strain; effective strain rate; bottom thickness; launch safety

2017-06-09；

2017-06-28

王小峰(1993—)，男，硕士研究生，主要从事炸药装药发射过载安全性研究。

陶钢(1962—)，男，博士，研究员，主要从事弹药设计及终点弹道毁伤研究,E-mail:taogang@njust.edu.cn。

10.11809/scbgxb2017.10.003

本文引用格式：王小峰，陶钢，丁贵鹏，等.30 mm小口径炮弹发射时炸药装药应变率及过载安全性分析[J].兵器装备工程学报，2017(10):9-14，20.

formatWANG Xiaofeng, TAO Gang, DING Guipeng, et al.Analysis of Strain Rate and Over-Loading Safety of Explosive Charge when 30 mm Small-Caliber Shell are Fired[J].Journal of Ordnance Equipment Engineering,2017(10):9-14，20.

TJ410.3；TJ55；TP391.9

A

2096-2304(2017)10-0009-06

(责任编辑周江川)