发射参数对航行体弹道安全性的影响

边晓阳,赵修平,朱长波,李显龙

(海军航空工程学院 a.研究生管理大队; b.飞行器工程系, 山东 烟台 264001)

【装备理论与装备技术】

发射参数对航行体弹道安全性的影响

边晓阳a,赵修平b,朱长波a,李显龙a

(海军航空工程学院 a.研究生管理大队; b.飞行器工程系, 山东 烟台 264001)

建立了带有阻尼板航行体水下发射与回落的弹道数学模型，以不同发射深度和出筒速度作为初始条件，对航行体弹道进行了仿真，得到了质心最大出水高度、最大入水深度以及z方向侧移量等在内的弹道特征参数，将发射后航行体尾端与发射点的最近距离作为安全性判定标准，分析了不同发射参数条件下，航行体弹道对发射载体的安全性影响。仿真结果表明：当发射深度为30 m、出筒速度为35 m/s时，航行体尾端与发射载体的最近距离达到最大，安全性最高。

发射深度；出筒速度；弹道仿真；安全性

某航行体是为日常训练设计的一型装备，在水下发射后需要回收以便再次使用，为了确保航行体再次落水后不会发生碰撞发射载体的危险，航行体尾部一侧加装了不对称分布的7块阻尼板(见图1)，水下发射后航行体尾部阻尼板迅速展开，在水流载荷和转动力矩的作用下进行减速并改变弹道方向，使得出水速度减小攻角增大，从而增大航行体与发射载体的距离[1]。阻尼板可以很大程度上降低航行体弹道对发射载体构成的危险，本文为进一步提高弹道安全性，进行了不同发射参数下的航行体弹道仿真分析，确定了安全性最高的发射参数方案。

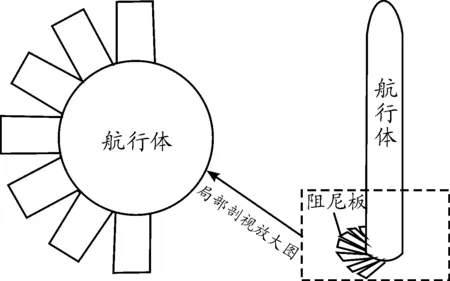
图1 阻尼板与航行体示意图

多年来，对水下航行体的弹道仿真从理论分析到数值模拟都被广泛研究。从理论分析方面来说，严卫生等[2]介绍了水下航行体的基本弹道理论模型以及建模时一些特殊情况，从数值模拟方面来说，李延军等[3]对冷发射水下飞行器进行了弹道仿真，同时介绍了出水过程中流体动力、附加质量以及附加质量导数等在内的数值计算方法；田宝国等[4]进行了有波浪力作用下的运载器水弹道研究；侯二虎、张宇文等[5]针对分离体的回落砸艇问题，建立了运载器尾部分离体的运动数学模型，得到了姿态角以及角速度等运动参数的变化规律；葛晖[6]分别建立了航行体的水下弹道模型以及分离体的下沉弹道模型，讨论了不同发射参数前提下分离体弹道对潜艇的安全性影响。

不管在理论方面还是数值模拟方面，目前关于水下发射航行体的弹道研究大多集中于具有作战效能导弹的水下弹道和出水弹道建模仿真，有关弹道安全性的研究也集中于“干”发射运载器的尾部分离体砸艇问题。关于以训练为目的且带有阻尼板的水下航行体研究，在弹道数学模型方面和弹道对发射载体安全性方面的研究较少。本文为该类航行体回落水后触碰发射载体的工程问题提供了理论依据，也对今后有类似功能的航行体安全性研究工作提供了借鉴参考。

1 坐标系选取及运动参数的定义

1.1 坐标系的选取

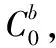
图2 发射坐标系与航行体坐标系示意图

1.2 运动参数的定义

航行体具有6个自由度，航行体坐标系相对于发射坐标系的位置就由6个坐标[7]确定：航行体坐标系坐标原点在发射坐标系中的3个坐标x，y，z和航行体坐标系与发射坐标系之间的3个欧拉角γ，ψ和θ。其中：θ为俯仰角，为航行体纵轴o0x0与水平面(oxz平面)的夹角，以航行体头部向上为正；ψ为偏航角，为航行体纵轴o0x0在水平面的投影与发射坐标系ox轴的夹角，从航行体尾部向前看时弹轴偏向参考航向o0x0的左侧为正；γ为滚转角，为航行体立轴o0y0与通过纵轴o0x0的铅锤平面间的夹角，从航行体尾部向前看时，顺时针滚动方向为正；所有方向均遵循右手螺旋规则。

2 航行体受力分析

航行体从水下发射后经历水中上浮段、出水段、空中飞行段、入水段和水中下沉段5个阶段，共受到流体动力、重力、浮力以及阻尼板阻力等力的作用[8-10]，其中流体动力按照流体介质将其分解成理想流体动力和黏性流体动力计算，具体的力学分析如下。

2.1 弹体阻力

(1)

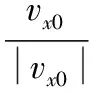
2.2 航行体尾部压力

航行体尾部压力是由附着在尾部的燃气泡产生的，其值由下式计算：

Fx2=PB·SB

(2)

其中：PB为尾部压强；SB为尾段截面积，尾部压强除水中段外其余阶段均为零。

2.3 净浮力及净浮力矩

净浮力是指作用在航行体上的浮力与重力之和，由于航行体坐标系选在质心，所以重力产生的力矩为零，浮力矩即为净浮力矩，具体表达式如下：

(3)

(4)

其中：

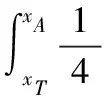
(5)

积分上限xA为航行体头部的x坐标；下限xT为航行体尾部的x坐标，若弹体已经开始出水，则xA为弹轴与水面交点的x坐标，d(x)为沿x轴处的航行体直径；(xc,yc,zc)为航行体浮心在航行体坐标系中的坐标。

2.4 横向力

根据细长体理论，全湿航行体所受横向力及力矩可以表示为

(6)

其中：ρ为流体介质的密度；Cd为黏性系数；Vy0和Vz0为航行体在航行体坐标系中的速度分量。

2.5 阻尼板阻力及阻尼力矩

如图3所示，单块阻尼板产生的力为：

(7)

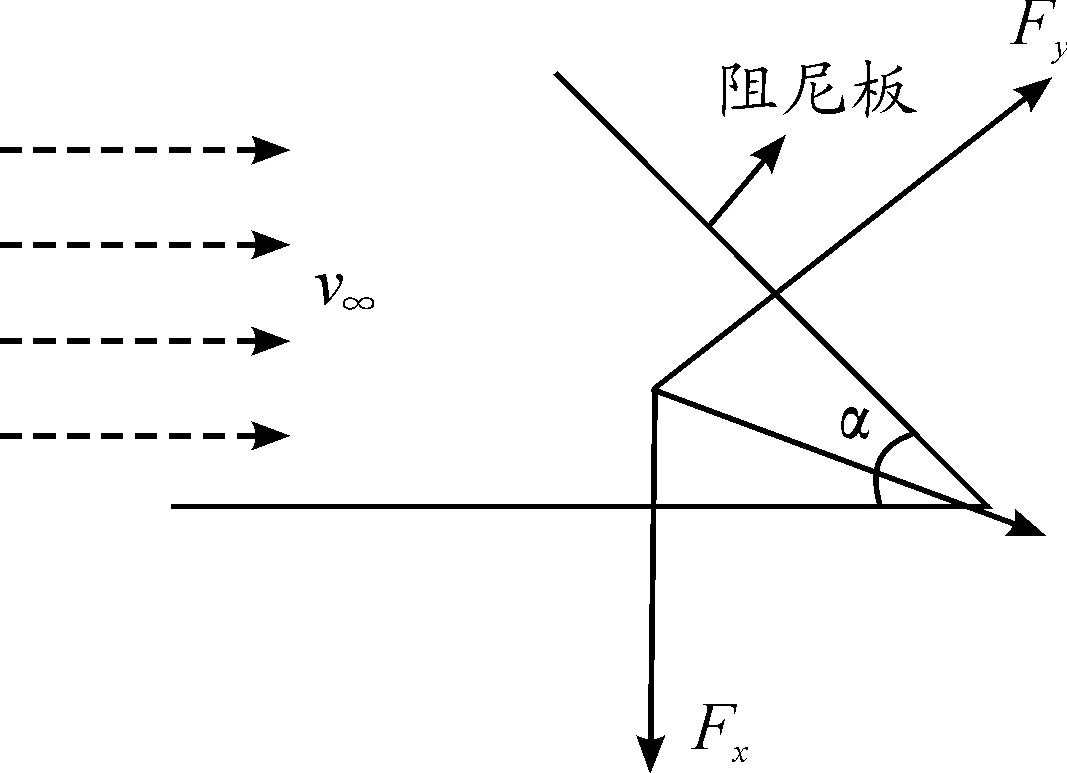
图3 单块阻尼板受力示意图

对航行体产生的合力和合力矩为

(8)

其中：nb为阻尼板个数；Sb0为阻尼板面积；α为阻尼板展开角度；Cd为平板阻力系数，xT为航行体尾部x坐标，R为弹体最大半径，xbi、ybi、zbi为阻尼板阻力作用点并且：

(9)

2.6 航行体附加质量

航行体同时关于xOy和xOz两个平面对称，则不为零的附加质量只有8个，即：

(10)

另外A44为零，A11与航行体质量相比是小量，但在航行体出水过程中，它的变化率并不小，并产生正的轴向力，致使导弹轴向加速，所以针对该航行体的弹道特殊性，A11在计算中不应忽略，其近似计算公式如下：

(11)

其中：μx和μy为修正系数。

综上，带有阻尼板的航行体受到总的外力及外力矩为

(12)

3 航行体运动方程组

3.1 航行体运动学方程

航行体的速度在航行体坐标系中3个轴的分量为(vx0,vy0,vz0)，根据航行体坐标系到发射坐标系的转换关系，可得到[11]

(13)

(14)

3.2 航行体动力学方程

根据动量定理和动量矩定理，航行体的动力学方程为：

(15)

(16)

将式(12)代入式(15)和式(16)可以得到航行体的动力学方程组为

(17)

4 仿真方案与结果分析

4.1 初始约束条件

航行体浮心靠近头部方向，再入水后将很快处于直立姿态，因此弹尾所处位置最深。所以将航行体发射再次落水后尾端与发射点的最近距离作为航行体弹道安全性的判定标准，通过计算，可得航行体质心各方向的行进距离同弹尾行进距离之间的换算公式

(18)

其中：(xt,yt,zt)为航行体尾端坐标；(xg,yg,zg)为质心坐标；xc为质心离航行体尾端距离，则航行体发射再入水后与发射载体的最近距离计算公式为

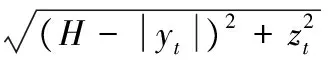
(19)

其中：H为发射深度；yt为航行体尾端的最大下沉深度；zt为航行体尾端水中下沉的最终侧移量。

航行体的质量取为40 T，长度取为10 m，发射载体的航行速度为3.5 kn。发射参数包括发射深度和航行体尾部出筒速度，由相关文献查得该类型航行体的发射深度一般为25～30 m，尾部出筒速度一般为30 ～35 m/s，以一个单位间隔对发射参数进行取值，并利用MATLAB软件[12]进行仿真分析，具体参数分配如表1所示。

表1 航行体发射参数取值

4.2 仿真结果分析

如图1所示具有阻尼板装置的航行体，其发射出筒后偏置轨迹主要是在zoy平面，所以对仿真结果进行分析时，有以下3个重点关注因素：质心y坐标随时间的变化趋势、质心z坐标随时间的变化趋势和质心在zoy平面的弹道变化轨迹。

1) 不同发射水深下弹道仿真结果分析

参照表1对发射水深进行取值，则发射深度分别取为25 m、26 m、27 m、28 m、29 m、30 m，此时出筒速度统一设定为 35 m/s。通过图4～图6并结合表2数据可以看出，随着发射水深由25 m增至30 m，航行体质心z方向的侧移量逐渐增大(由12.28 m增大至18.08 m)，出水最大高度逐渐减小(由15.62 m减小至6.06 m)，这是由于发射水深越大，阻尼板在水中产生的阻尼力和阻尼力矩对航行体作用影响时间越长；观察图5并结合表2数据中的出入水时刻可以发现，当发射水深变大时，出水时刻滞后，入水时刻提前，并且出入水时间逐渐增大，这是由于发射水深的变化影响了航行体的出入水速度，间接改变了出入水的起始时刻和时间间隔；根据计算求得的航行体入水后尾端与发射点的最近距离。发射水深为30 m时航行体再入水后与发射载体的最近距离值最大，为26.01 m，即发射水深为30 m时弹道对发射载体最为安全。

图4 质心y坐标随时间变化曲线

2) 不同出筒速度下弹道仿真结果分析

参照表1对出筒速度取值为 30 m/s、31 m/s、32 m/s、33 m/s、34 m/s、35 m/s，此时发射深度统一设定为25 m。通过图7～图9并结合表3数据看出，随着出筒速度的增大，航行体在阻尼板产生的阻尼力和阻尼力矩的综合作用影响下，质心z方向的侧移量逐渐增大，出水最大高度逐渐减小；观察图8并结合表3的出入水时刻可以发现，随着出筒速度逐渐变大，出水时刻提前，入水时刻滞后，与图5对比可知，出筒速度对出入水时刻的影响较小。最后根据计算得出的航行体入水后与发射点的最近距离。发射水深为35 m/s时航行体弹道对发射载体最为安全，但相对于发射水深来说，出筒速度对安全距离的影响不大，为弱相关因素。

图5 质心z坐标随时间变化曲线

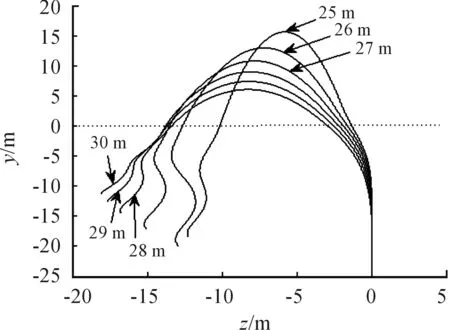
图6 质心在zoy平面弹道变化轨迹

航行体发射深度/m质心出水最大高度/m质心入水最大深度/mz方向终点侧移量/m航行体终点俯仰角/(°)航行体终点偏航角/(°)最近距离/m出入水时刻/s出水开始时刻出水结束时刻入水开始时刻入水结束时刻2515．6218．4412．2896．188．3013．020．431．084．354．492612．9819．9512．9793．539．3413．440．471．153．984．262710．8017．0915．1093．0510．2017．170．531．233．634．14288．9714．3616．7791．778．1320．970．581．313．384．00297．4012．5917．6490．474．5723．770．651．403．203．85306．0611．2218．0889．791．2526．010．721．493．063．71

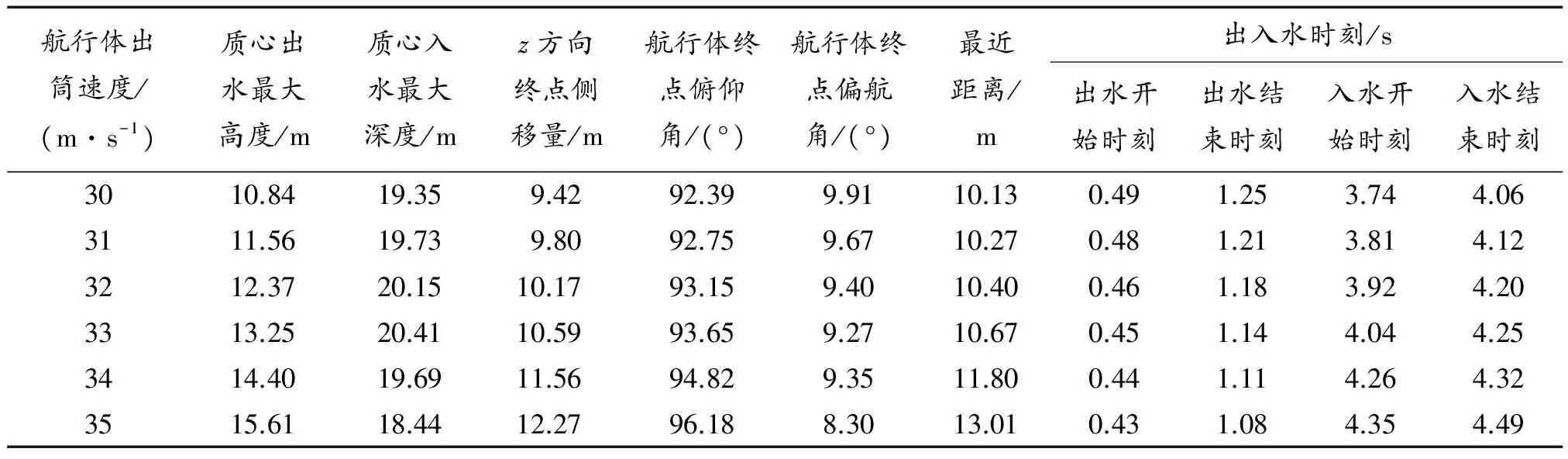
表3 不同出筒速度航行体弹道特征点数据

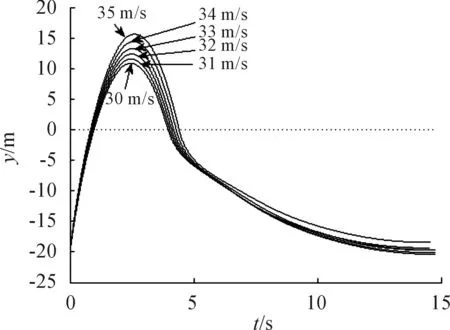
图7 质心y坐标随时间变化曲线

图8 质心z坐标随时间变化曲线

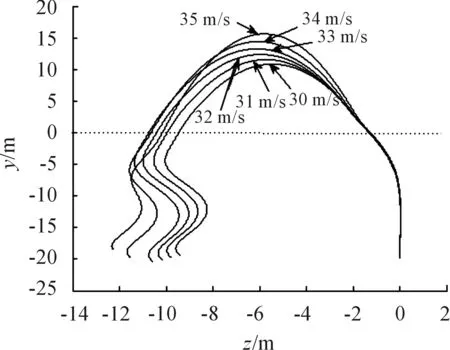
图9 质心在zoy平面弹道变化轨迹

5 结论

在建立了半闭合航行体弹道数学模型的基础上，对不同发射水深、出筒速度情况下航行体弹道进行了仿真，结果表明，发射水深是影响航行体弹道对发射载体安全性的强相关因素，在航行体的规定发射参数范围内，发射水深为30 m，出筒速度为35 m/s时，航行体再入水后与发射载体距离最远，弹道安全性最高。

[1] 都军民,孙卓,魏建峰.舵板张开过程的数值仿真与试验研究[J].机械科学与技术,2013,32(3):426-429.

[2] 严卫生.鱼雷航行力学[M].西安:西北工业大学出版社,2005.

[3] 李延军,郭凤美,董利强.水下飞行器的弹道仿真[J].导弹与航天运载技术,2009(6):1-4.

[4] 田宝国,耿霆.波浪力作用下无动力运载器水弹道仿真[J].计算机与数字工程,2011,39 (1):7-9.

[5] 侯二虎,张宇文.潜射运载器尾部分离体水下运动仿真[J].计算机仿真,2012,29(8):31-34.

[6] 葛晖.潜射导弹发射安全性研究[D].西安：西北工业大学,2004.

[7] 王占莹,冯健华,程少华，等.航行体出水俯仰双态特征研究[J].兵器装备工程学报,2016,37(3):163-166.

[8] 李杰，鲁传敬，陈鑫.附着空泡对潜射导弹弹道影响分析[J].弹道学报，2014(3)：54-58.

[9] SMALLWOOD D A,WHITCOMB L L.Model-based dynamic positioning of underwater robotic vehicles:th eory and experiment[J].Oceanic Engineering,IEEE Journal,2004,29(1):169-186.

[10] 宋海龙.水弹道建模与仿真方法研究[D].哈尔滨:哈尔滨工业大学,2014.

[11] 齐强,陈志刚,周源.航行器水中运动数学模型及数值仿真[J].舰船科学技术,2014,36(5)：80-83.

[12] 薛定宇，陈阳泉.高等应用数学问题的Matlab求解[M].北京：清华大学出版社，2004:209-217.

[13] 王占莹， 程少华，于海涛，等.大水深垂直发射航行器水弹道稳定性分析[J].兵工自动化，2016(6):1-5.

StudyontheInfluenceofLaunchParametersontheSafetyofVehicleTrajectory

BIAN Xiaoyanga， ZHAO Xiupingb, ZHU Changboa， LI Xianlonga

(a.Graduate Students Brigade; b.Department of Airborne Vehicle Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)

The mathematical model of the underwater launching and falling trajectory with rudder is established. At the same time,taking the different depth of launch and the speed of the barrel as the initial condition, we simulated the trajectory of the vehicle.The trajectory characteristic parameters such as the maximum water discharge height, the maximum water depth and the lateral displacement of the z direction are obtained. Then,the influence of the ballistic trajectory on the safety of the launch carrier under different emission parameters is analyzed, taken the nearest distance between the aeronautical heart and the launching point after the launch as the safety criterion.The simulation results show that when the depth of launch is 30m and the velocity of the shot is 35 m/s, the nearest distance between the aeronautical heart and the launch carrier is the maximum and the safety is the highest.

launch depth; barrel speed; trajectory simulation; security

2017-06-10；

2017-06-29

边晓阳(1993—)，男，硕士研究生，主要从事发射系统与集成技术研究。

赵修平(1963—),男，硕士，教授，主要从事导弹发射工程研究。

10.11809/scbgxb2017.10.009

本文引用格式：边晓阳,赵修平,朱长波,等.发射参数对航行体弹道安全性的影响[J].兵器装备工程学报，2017(10):40-45.

formatBIAN Xiaoyang， ZHAO Xiuping, ZHU Changbo, et al.Study on the Influence of Launch Parameters on the Safety of Vehicle Trajectory[J].Journal of Ordnance Equipment Engineering,2017(10):40-45.

TJ02

A

2096-2304(2017)10-0040-06

(责任编辑周江川)