锅炉风道振动模拟分析

张 进 段 权 侯兴龙 白文杰

(西安交通大学化学工程与技术学院)

锅炉风道振动模拟分析

张 进 段 权 侯兴龙 白文杰

(西安交通大学化学工程与技术学院)

锅炉风道振动严重影响设备的安全运行，其中最常见的是由于气流脉动引起的风道共振。通过有限元模拟进行风道的固有频率分析和谐响应分析，得到风道结构的固有频率，以便在设计或改造过程中避开气流脉动频率从而避免发生共振。计算结果表明风道的固有频率分布密集时，难以通过加固风道的方式消减振动，需改善气体的流动状态。

锅炉 风道 振动 模态分析 谐响应

锅炉风机是一种重要的机械设备，送风管道系统的安全平稳运行直接影响到锅炉的运行。大型锅炉的风道较长，空气流量较大，为减小流动阻力，风道截面设计尺寸往往很大，且风道壁厚较薄(一般由厚度为3～10mm的钢板焊接而成)，因此风道刚度较差，在激振力的作用下容易引起振动[1]。其次，风道内的空气流速较快，在通过转角和大小头时，容易产生涡流，引起振动和噪音[2，3]。如果风道设计不合理，就会产生共振或出现强涡流区，引起风道强烈振动，严重威胁锅炉设备的安全运行。

1 风道振动原因分析

锅炉风道内介质的流动通常是不稳定的，存在一定的脉动，因此容易引起风道的振动。最常见的是风道共振，引起共振的主要原因有：风道内介质的脉动存在一个振动频率，如果某段风道的固有频率与管道内气流的压力脉动频率耦合，则会引起共振[4]；由流体力学可知，风道内流体的湍流流动本身存在一个含主导频率的频带振动[5]，若该主导频率与风道固有频率一致则会引起共振；风道局部涡流生成的卡门漩涡会引起周围的静压振动[6]；风道内气流的声驻波具有无限的谐波，只要卡门漩涡引起的激振频率与气流声驻波的任一谐波频率耦合，就会发生共振[7]。引起锅炉风道振动的原因非常复杂，笔者主要从结构方面讨论风道的振动设计。

2 模态分析

2.1 模态分析理论基础

模态分析作为机械结构动力学研究的基础，可以得到分析对象的动态特性，包括其固有频率和振型[8]。当结构受到的动态载荷激励频率与固有频率相一致时，会产生较大的共振，导致出现较大的位移和应力，对结构的性能产生不利影响，这在结构设计时是应该避免的。

根据机械系统振动理论[9]，结构系统的振动微分方程一般形式为：

(1)

式中 [m]、[c]、[k]——质量矩阵、阻尼矩阵、刚度矩阵；

{x(t)}——位移向量，{x(t)} =[x1，x2，…，xn]T；

{F(t)}——激振力向量，{F(t)}=[f1，f2，…，fn]T。

在利用静态模态分析求解自由振动的固有频率和振型时，假设不受外力作用，则振动微分方程中的激振力向量{F(t)}={0}，且忽略阻尼的影响，式(1)可简化为无阻尼自由振动的运动微分方程：

(2)

任何弹性体的自由振动均可分解为一系列简谐振动的叠加，设式(2)有以下简谐振动解：

x(t)={φ}isinωit

(3)

将式(3)代入式(2)可得：

(4)

要使{φ}i有非零解，则必有：

(5)

其中，{φ}i为第i阶固有频率振型的特征向量，这就归结于求解特征值的问题，ωi是结构系统第i阶固有频率，i=1，2，…，n。由以上分析可知，结构系统有n个固有频率和主振型，每个固有频率和对应主振型都代表着单自由度系统自由振动的模态。

2.2 风道的有限元模型

根据风道结构图纸，风道总长28.65m，壁厚5mm，加强筋有扁钢和角钢两种，其规格见表1。

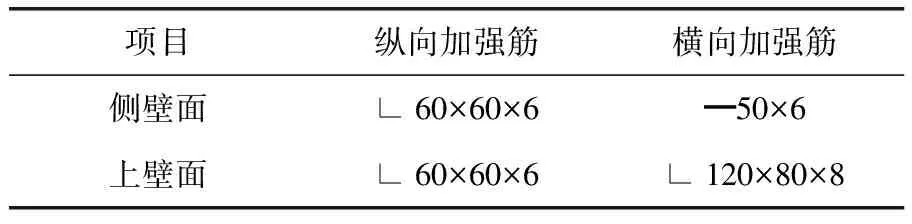
表1 风道加强筋规格 mm

由此建立风道的三维实体模型[10，11]，如图1所示。

图1 风道的三维实体模型

风道材料采用结构钢，密度ρ=7850kg/m3，泊松比μ=0.3，杨氏弹性模量E=200GPa。定义单元类型为SOLID187，该单元是一个高阶三维十节点固体结构单元，SOLID187具有的二次位移模式可以更好地模拟不规则的模型[12]。在网格划分过程中，为确保计算结果的精确度，应控制网格的大小。由于风道结构整体模型和壁厚的尺寸差别较大，不适合使用质量较高的网格，故采用自适应网格划分。

根据图纸所示的结构支承情况，在下壁面相应位置施加边界约束条件，P1、P2两处为滑动约束，P3～P7共5处为固定约束。风道两端均采用软管连接，故在风道两端接口处不添加约束(图2)。

图2 风道结构约束情况

2.3 计算结果

经计算得到风道整体结构部分阶次固有频率见表2。

表2 风道整体结构部分阶次固有频率

由表2可见，风道的各阶固有频率分布非常密集。为了便于分析，需对风道结构进一步简化。因风道为薄壁结构，根据其变形特点，分别取侧壁面和上壁面进行分析。侧壁面和上壁面的有限元计算模型如图3、4所示。

图3 风道侧壁面有限元模型

图4 风道上壁面有限元模型

2.3.1 侧壁面计算结果

经计算得到侧壁面部分阶次固有频率见表3。

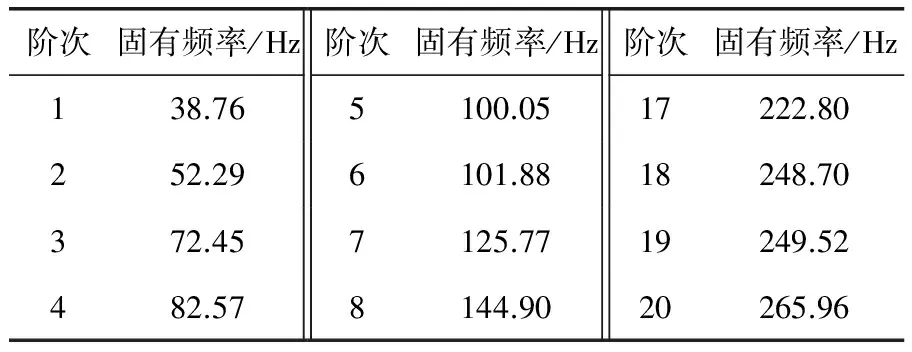
表3 风道侧壁面部分阶次固有频率

典型的风道侧壁振型如图5所示。

a. 2阶振型

b. 19阶振型

为确定是否发生共振，计算锅炉风机的激振频率。锅炉风机的型号为53-KB-1401，其转速为1 485r/min，风机叶片数为10，风道内气流脉动激发频率fp为：

(6)

式中m——风机转速；

n——风机叶片数。

故气流脉动激发频率为247.5Hz。由表3的计算结果可以看出，第18、19阶固有频率接近风道内气流脉动激发频率，由于共振使其振动非常剧烈。同时由计算结果发现，振动阶数越高，则振动幅度越小，这是由于阶数越高，振型节点越多，而每一个振型节点都相当于一个自然固定约束，因此振动的幅度随着阶数的增加而减小。

2.3.2 上壁面计算结果

经计算上壁面前12阶固有频率见表4。

表4 风道上壁面前12阶固有频率

典型的上壁面振型如图6所示。

a. 1阶振型

b. 11阶振型

计算结果表明，固有频率接近247.5Hz时的振动最明显，并且由于上壁面的横截面比侧壁面大，其振动幅度大于侧壁面。将计算结果与实际测量数据相比较发现，振动幅度最大的位置与实际风道的振动最大段相吻合，故模拟结果具有较高的可信度。

3 谐响应分析

3.1 谐响应分析理论基础

谐响应分析主要是用于确定线性结构在承受随时间按正弦规律变化的载荷时的稳态响应[13]，运动方程为：

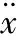
(7)

其位移响应为：

|x|=|A|sin(θt+φ)

(8)

其中，φ为位移响应滞后激励载荷的相位角，A为位移幅值向量，θ为激振力的频率，其余符号同上。

谐响应分析过程中只计算结构的稳态受迫振动，不考虑激振开始时的瞬态振动。谐响应分析的目的在于计算出结构在几种频率下的响应值(通常是位移)对频率的曲线，从而使设计人员能预测结构的持续动力特性，验证设计能否克服共振、疲劳和其他受迫振动引起的有害效果[14，15]。

3.2 侧壁面谐响应分析

根据现场振动测试数据，振动频谱内25、50、250Hz频率成分占优，因此主要对这3个频率进行谐响应分析，分析结果如图7所示。

a. 25Hz

b. 50Hz

c. 250Hz

不同频率、不同开度下最大振动点的振动幅值变化趋势如图8所示。

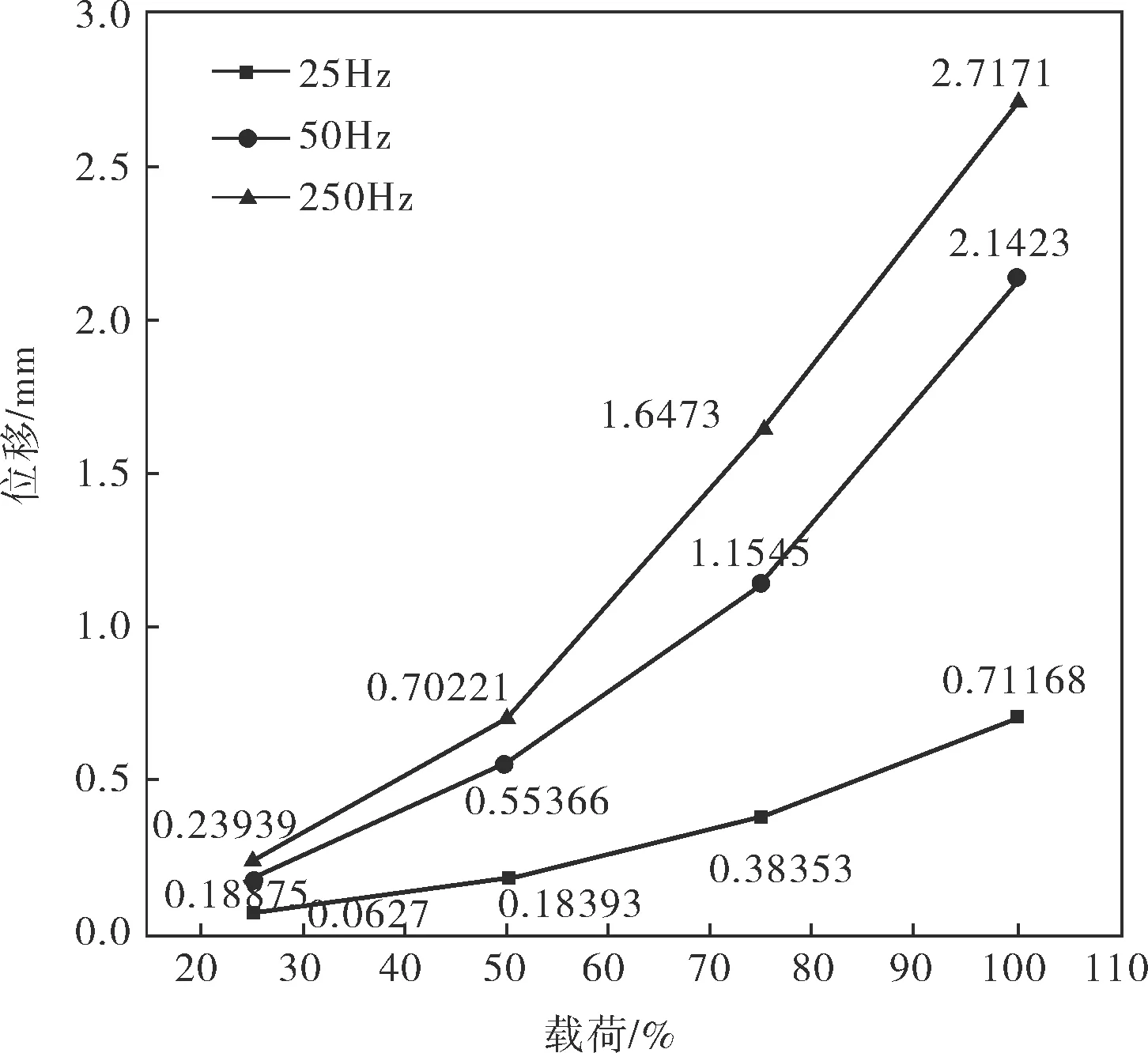
图8 不同频率、不同开度下最大振动点的振动幅值变化趋势

由图8可见，在不同开度下50、250Hz的谐响应远大于25Hz，这是由于侧壁面第18、19阶固有频率均很接近247.5Hz，第2阶固有频率则接近50Hz，容易发生共振，而25Hz则远小于侧壁面的一阶固有频率38.76Hz，故不易激起共振。

3.3 上壁面谐响应分析

与侧壁面类似，针对25、50、250Hz这3个频率对风道上壁面进行谐响应分析，结果如图9所示。

a. 25Hz

b. 50Hz

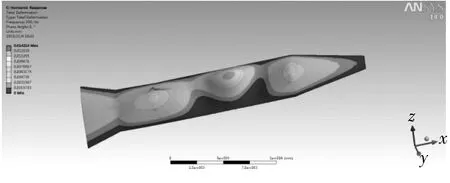
c. 250Hz

上壁面不同频率各开度时谐响应最大振动点的幅值变化趋势如图10所示。

图10 上壁面不同频率各开度时谐响应最大振动点的幅值变化趋势

由图10可见，在不同开度下频率越高谐响应越小，参考表4中固有频率的计算结果，可知这是由于上壁面第1阶固有频率很接近25Hz，而第3阶固有频率则很接近50Hz，故第1、3阶的共振容易被激发起来，而直到第11、12阶都与250Hz有一定频率间隔，而且低阶共振更容易被激发，因此250Hz谐响应较小。

4 结论

4.1 锅炉送风风道作为一种薄壁结构，其振动与部分频率的共振有关，但是由于固有频率密集，仅通过加强筋加固难以达到理想的减振效果，需要进一步改善流体的流动状态以减小振动。

4.2 风道的某些高阶固有频率与气流脉动激发频率比较接近，并且根据振动测试结果，250Hz也是振动频谱上比较明显的峰值频率，由此可知，250Hz附近的振动和风机通过频率有关。

4.3 高阶振型中存在较多的振型节点，每一个振型节点相当于一个自然固定约束，故高阶振型的共振振幅较小，同时表明在振型节点处添加约束没有意义。

4.4 由谐响应分析可知，高阶共振不容易被激发，因此应优先控制低阶振型的共振。

4.5 在风道设计过程中，应采取合理的措施使其固有频率避开气流的脉动频率，以免发生共振导致风道损坏。

[1] 张智达，张春阳.基于CFD方法的锅炉冷风管道振动原因分析[J].东北电力大学学报，2010，30(6)：1～4.

[2] 龙航.浅析火电厂一次风机出口风道的振动故障及处理[J].中国新技术新产品，2015，(18)：85～86.

[3] 冯钧，仇雷敏，朱耀先，等.郑州热电厂冷风道振动分析及其治理[J].热力发电，2000，29(5)：50～51.

[4] 王伟，赖永星，苗同臣，等.振动力学与工程应用[M].郑州：郑州大学出版社，2008.

[5] 杨建国，张兆营，鞠晓丽，等.工程流体力学[M].北京：北京大学出版社，2010.

[6] 杨国旗，郁翔，李平，等.330MW机组锅炉尾部烟道振动分析[J].陕西电力，2010，38(5)：77～79.

[7] 杜利梅，陈志波，刘殿玮.锅炉一次风暖风器及附属风道振动机理研究[J].黑龙江电力，2013，35(3)：247～249.

[8] 余俊，刘永平，章慧成，等.蜗线齿轮有限元模态分析[J].机械设计与制造，2015，(12)：139～141.

[9] 李有堂.机械振动理论与应用[M].北京：科学出版社，2012.

[10] 浦广益.ANSYS Workbench基础教程与实例详解[M].北京：中国水利水电出版社，2013.

[11] 王欣.薄壁烟风道有限元分析及设计计算优化的程序实现[D].南京：东南大学，2006.

[12] 黄志新，刘成柱.ANSYS Workbench 14.0超级学习手册[M].北京：人民邮电出版社，2013.

[13] 刘涛，王卫辉，鹿飞，等.基于Workbench的箱形伸缩臂模态及谐响应分析[J].制造业自动化，2015，37(4)：80～82.

[14] 刘阔，刘春时，林剑峰，等.VMC0540d 机床床身和立柱结构的谐响应分析[J].机械设计与制造，2011，(12)：162～164.

[15] 武永红，李永堂，刘志奇.输液管道的振动分析[J].振动·测试与诊断，2013，33(z2)：100～104.

SimulationAnalysisofBoilerAirDuctVibration

ZHANG Jin, DUAN Quan, HOU Xing-long, BAI Wen-jie
(SchoolofChemicalEngineeringandTechnology,Xi’anJiaotongUniversity)

The boiler’s air duct vibration caused by the gas pulsation seriously influences equipment security. Through having FEM based to analyze harmonic response and intrinsic frequency of the air duct, the air duct’s intrinsic frequency was obtained so that the gas pulsation frequency can be avoided in the design or in the air duct renovation. The calculation results show that, when dense distribution of the air duct’s intrinsic frequency exists, reducing the vibration by reinforcing air duct only becomes difficult; and improving the air flow state in the air duct has to be considered.

boiler, air duct, vibration, modal analysis, harmonic response

张进(1993-)，硕士研究生，从事动力工程与工程热物理的研究。

联系人段权(1968-)，副教授，从事石油化工企业设备长寿运行评价研究、结构疲劳断裂强度分析、结构完备性评价与动机组工况监测机械减振降噪分析的工作，quanduan@mail.xjtu.edu.cn。

TQ054

A

0254-6094(2017)02-0196-06

2016-03-29，

2016-11-30)