基于卡尔曼滤波器的主燃油计量装置故障诊断

芦海洋，王 曦

基于卡尔曼滤波器的主燃油计量装置故障诊断

芦海洋1,2，王 曦1,2

（1.北京航空航天大学能源与动力工程学院；2.先进航空发动机协同创新中心：北京100191）

为了建立主燃油计量电液执行机构（EH A）的故障诊断算法，分析了主燃油计量液压机械控制装置的工作原理，提出了1种建立主燃油计量线性变参数(LPV)模型的方法，设计并得到基于离散卡尔曼滤波器的主燃油计量电液执行机构位移输出的残差生成器。仿真结果表明：该残差生成器具有对故障敏感而对噪声和建模误差不敏感、对残差的动态响应快，幅值变化较大的特点，有效降低故障误报警率和漏报警率。

主燃油计量装置；故障诊断；卡尔曼滤波器；执行机构；线性模型

0 引言

卡尔曼滤波器的研究始于20世纪60年代，那时的计算机技术还不成熟，维纳滤波技术尽管已经产生，但是需要大量历史数据，不具备实现条件，然而卡尔曼滤波器状态估计的迭代更新过程不需要存储大量历史数据，从而解决了当时硬件的存储限制问题[1]。

很多研究学者将卡尔曼滤波应用于工程（如故障诊断和参数估计）中解决实际问题。目前，卡尔曼滤波被分为传统卡尔曼滤波、拓展卡尔曼滤波、混合卡尔曼滤波。传统卡尔曼滤波主要用于线性系统中；随着工程应用的发展，对非线性系统的研究越来越多，研究学者将传统卡尔曼滤波发展为拓展卡尔曼滤波(EKF)，解决了传统卡尔曼滤波在非线性模型参数估计中的应用限制问题。Y.Chinnia等[2]将拓展卡尔曼滤波器(EKF)用于估计黏性摩擦系数和有效体积模量2个参数，将待估计的系统参数的变化和电液执行机构(EHA)的故障联系起来，例如，黏性摩擦系数的变化表明液压油的变质和密封件的磨损，有效体积模量的减小影响闭环系统的响应；Xudong Wang等[3]应用基于拓展卡尔曼滤波器的多模型(MM)估计来实现对电液执行机构系统的故障诊断、定位，其原理是将某一故障和1组拓展卡尔曼滤波器相关联，某一组卡尔曼滤波器的残差变大时，表明与其关联的故障发生；L.An等[4-5]将拓展卡尔曼滤波器用于估计电液伺服阀阀芯位移、作动筒内的腔压、活塞的速度等变量，将待估计的参数和实际参数作比较得到残差，当故障发生时，与故障对应的残差生成器的残差值变大，不同程度的泄漏故障对应不同的残差值，通过阈值的选定实现了对泄漏程度的分类。

随后，研究学者又将目光放在混合卡尔曼滤波(HKF)的研究上。Takahisa Kobayashi、Donald L.Simon[6-7]将混合卡尔曼滤波应用于航空发动机在线诊断，其研究成果已被NASA所验证。该方法将非线性系统和线性系统结合，具体做法是将非线性系统的状态变量和输出作为线性系统的稳态值，估计输出和测量输出的差值经过卡尔曼增益后反馈到线性系统中。

无论以上何种形式的卡尔曼滤波器，始终不可避免的问题是线性化，针对以上问题，本文提出了1种将电液执行机构(EHA)特性归一的线性化方法，该方法可以避免设计卡尔曼滤波器时调度参数A、B、C、D。

1 主燃油计量装置工作原理

主燃油计量活门是航空发动机中供油系统的主要组成部分，其控制组件如图1所示。目前，全权限电子控制器（FADEC）[8]采用电液伺服阀、主燃油计量活门、压差活门与回油活门的伺服控制组件的形式来实现对主燃油计量出口油量的控制。

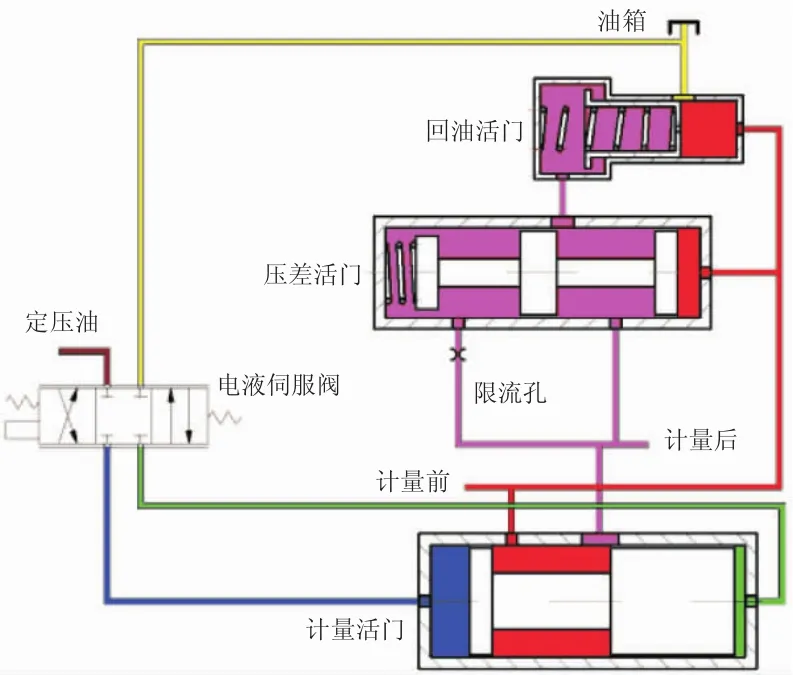
图1 主燃油计量活门控制组件

设发动机按等转速控制计划调节，在稳态平衡条件下，发动机转速不变，齿轮泵供油量一定，计量活门的位置一定，燃油流通面积一定，压差活门和回油活门的位置保持不变，回油量一定，因此，向发动机的供油量保持不变，计量活门前、后压差保持不变。当飞行高度升高时，发动机空气流量减少，所需供油量减少，而供油量未变，故发动机转速增加，又引起供油量相应增加，计量活门前、后油压差增大，于是压差活门左移，开大了回油活门左腔与压差活门中间腔之间的流通面积，回油活门左腔压力下降，回油活门在压差力作用下左移，回油量增多。计量活门前油压下降，计量装置前、后油压差减小，直至恢复到压差控制器所调定的压差值为止。调节结束后，压差活门稍偏左，回油活门偏左，回油孔开大，回油量增加，计量活门前、后压差基本不变，因此，主燃油计量装置中设计了等压差活门，使计量的燃油流量仅为计量活门开度的正比例关系。当计量活门开度不变时，发动机供油量基本不变，而油气比的增加必然导致发动机转速的增加，在转速闭环控制的作用下，电液伺服阀的工作电流按转速偏差调节，关小计量活门的开度，直至使转速回到设定指令值为止。

压差活门可以保证主燃油计量活门出油孔前、后压差控制，因此等压差控制使得计量活门出口的油量Q仅仅由计量活门的开度面积决定

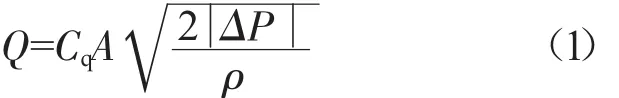
式中：Cq为流量系数[9]；A为计量活门的开度面积；ΔP为计量活门前、后的压差；ρ为燃油的密度。

由式（1）可知，当主燃油计量前、后ΔP一定时，计量出口的流量由开度面积决定，而在目前全权限数字电子控制[10-12]中，计量活门的运动受到电液伺服阀的控制。电子控制器采集计量活门的LVDT位移传感器信号与指令信号位置作差，其值经过PI控制器计算后输入到电液伺服阀的电信号接口中，从而调整电液伺服阀的阀芯开度，调制送往计量活门作动2腔的流量，主燃油计量活门负反馈控制结构如图2所示。

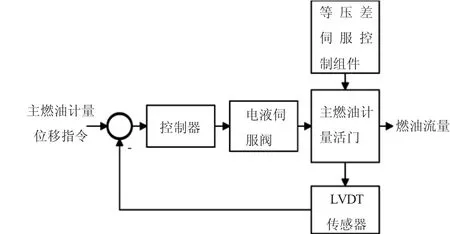
图2 主燃油计量活门负反馈控制结构

根据主燃油计量液压机械控制装置非线性AMESim模型仿真数据，通过最小二乘法辨识的方法可以得到电液伺服阀输出流量随不同阶跃输入的归一化响应曲线的线性模型，线性化之后的模型可以用于设计卡尔曼滤波器，采用Kalman滤波估计算法[13-14]的优点在于能弥补建模误差。尤其是非闭环控制回路的建模，建模误差将被放大，采用Kalman滤波估计算法可以有效地削减该误差，避免了在正常无故障情况下的误报警概率。基于Kalman滤波的主燃油计量活门FMV控制回路的故障诊断结构如图3所示。

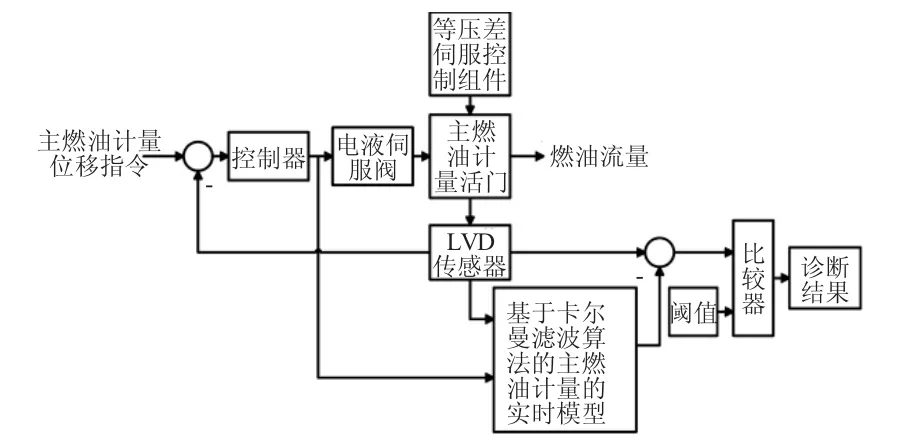
图3 主燃油计量控制回路故障诊断策略

2 主燃油计量运动线性模型

该主燃油计量运动线性模型的结构形式如图4所示。

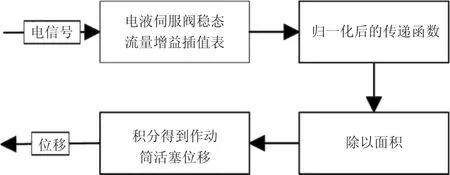
图4 主燃油计量运动数学模型结构形式

电液伺服阀中的电信号与调制输出的流量是一一对应的关系，电液伺服阀阀芯开度面积越大，输出到计量活门作动2腔中的流量越多，计量活门的作动速度越快。电液伺服阀稳态流量增益曲线如图5所示，数据见表1。

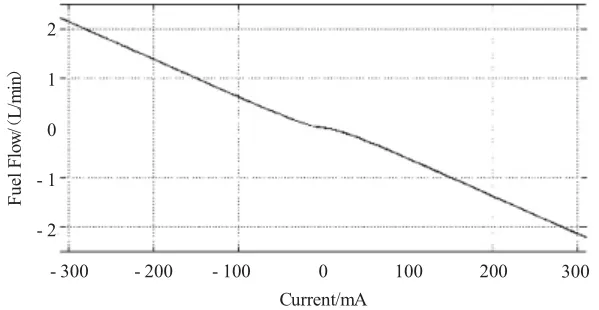
图5 电液伺服阀稳态流量增益曲线

表1 电液伺服阀稳态流量增益数据

当电液伺服阀采用不同的阶跃输入信号时，电液伺服阀输出流量的响应曲线如图6所示。

假设待辨识的流量响应的传递函数具有如下离散形式

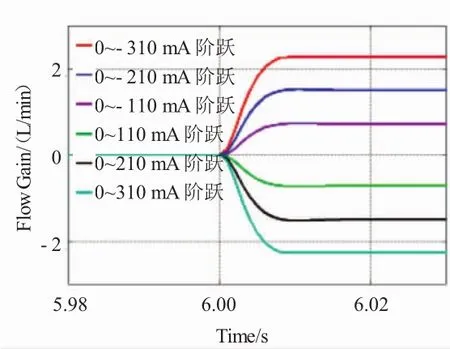
图6 电液伺服阀流量动态响应曲线

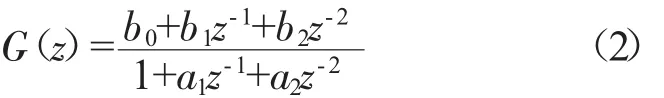
利用最小二乘法对图6中的6条响应曲线进行时域辨识，可以得到与之相对应的6个传递函数，各传递函数的参数（由于篇幅有限，对参数进行了约简）见表2。

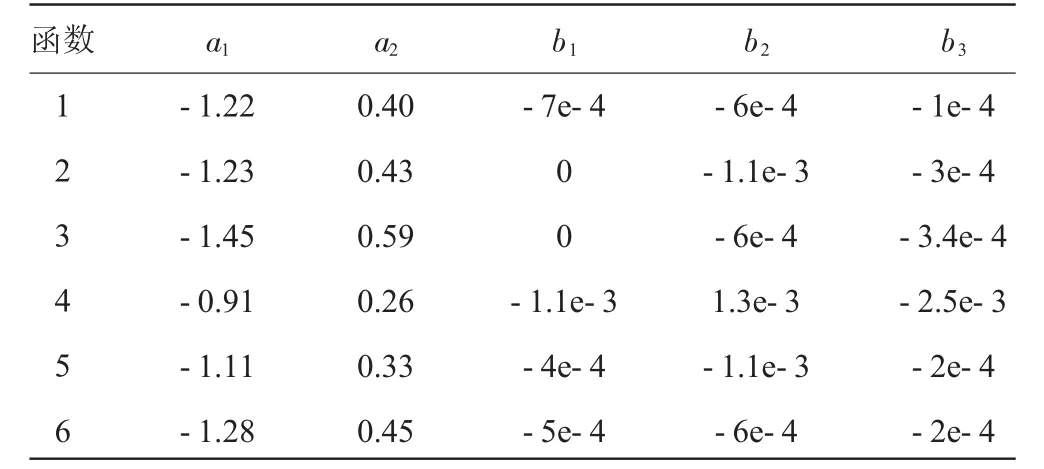
表2 6个传递函数的参数

所有传递函数的极点位置如图7所示。

这6个传递函数的关于输入的响应稳态值见表1，在建立电液伺服阀输出流量的数学模型时，稳态值可以根据调度

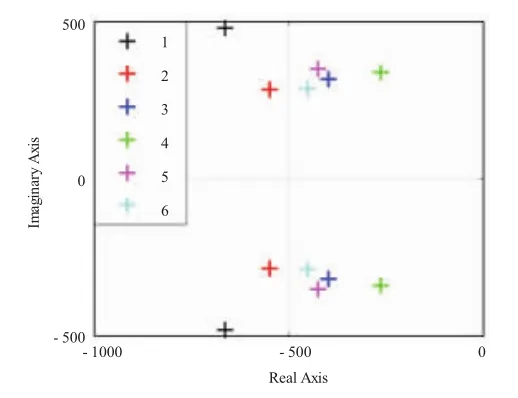
图7 6个传递函数的极点位置

得到，动态过程通过辨识得到，也就是说只需要关注图6的6条动态响应曲线的动态响应品质。本文列出了2个衡量动态品质的参考量：调节时间和超调量。对于2阶传递函数，有

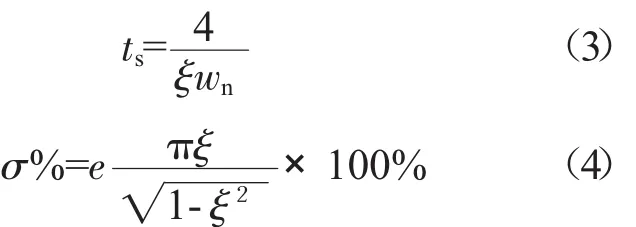
统计得到6个传递函数的调节时间ts和超调量σ，见表 3。

从表3中可见，6个传递函数的调节时间比较相近，且超调量也在较小范围内变动，工程中为了简化设计过程，可以近似认为该电液伺服阀的动态响应品质是相等的。通过将图6中的动态响应曲线相对表1中的稳态数据进行归一化处理后也发现，在不考虑稳态流量输出的情况下，6条动态响应曲线是近似相近的，如图8所示。

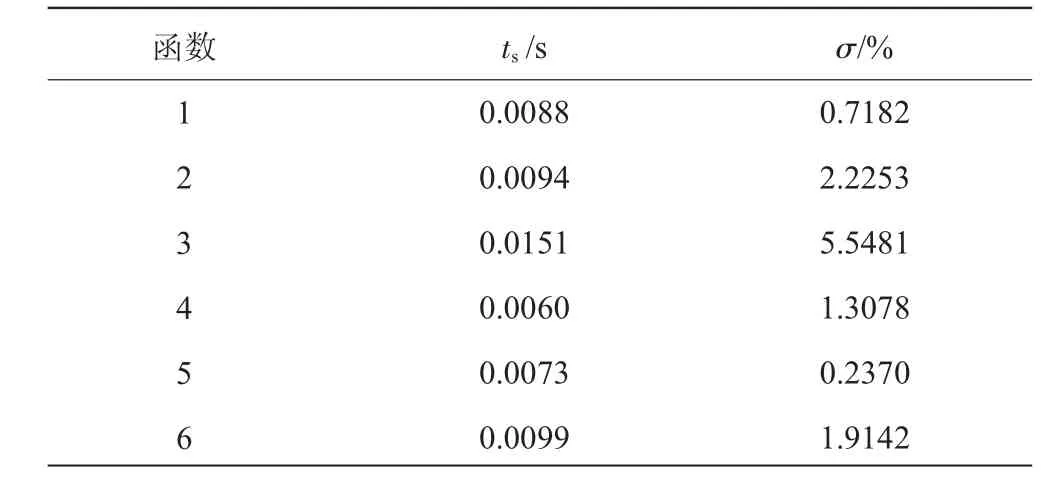
表3 6个传递函数的响应时间和超调量

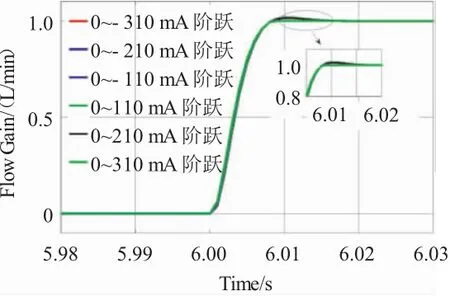
图8 归一化处理后的电液伺服阀流量动态响应曲线

综合考虑表3中的参数后，选取图8中的1条曲线作为待辨识的归一化的传递函数，假设经归一化后的离散状态空间方程

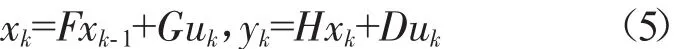
式中：输入u为控制器的电流值；yk是经归一化后线性模型的输出[0.08131 0]，D=0。

由于以上模型不带有电液伺服阀稳态流量增益的信息，只是表征了其动态响应的过程，将表1作为待调度的稳态流量增益数据表，可以基于参数调度建立电液伺服阀输出流量线性模型，设计过程如下。

假设电液伺服阀输出流量随输入电信号的调度函数为

电液伺服阀输出流量的线性模型具有如下形式

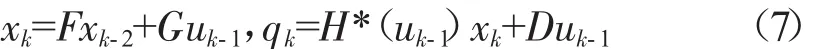
式中：H*（uk-1）=σ（uk-1）H；qk为电液伺服阀流量输出。

根据控制器电信号阀流量输出线性模型结构如图9所示。

假设主燃油计量活门的速度

式中A为主燃油计量活门作动腔的径向横截面积。

假设采样周期Ts，主燃油计量活门的位移S可以表示为

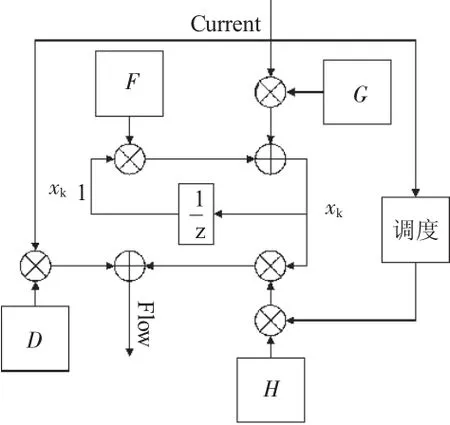
图9 电液伺服阀输出流量线性模型

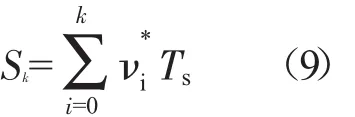
3 离散卡尔曼滤波器的设计

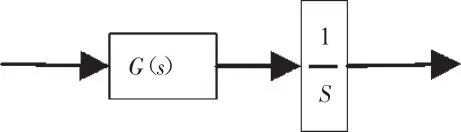
图10 经积分后的新系统

图4 中的“除以面积”环节只是对电液伺服阀输出流量的变换，为一固定的系数，其物理结构上应该位于传递函数之后，但从数学角度看，其位置在传递函数之前还是传递函数之后都一样，本文将其放在传递函数之前，传递函数和1个积分环节串联到一起，如图10所示。

该过程用数学可以表示为

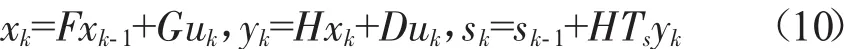
假设增广后的状态变量x1k

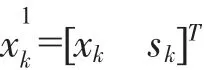
图10中的模型经过增广后并考虑噪声的线性模型可以表示为

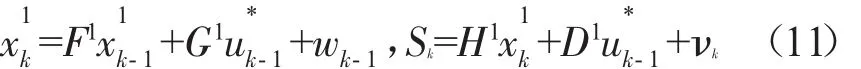
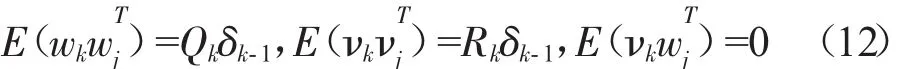
δk-1是 Kronecker-δ函数

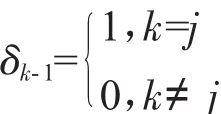
假设卡尔曼滤波器需要预定义的初始参数为

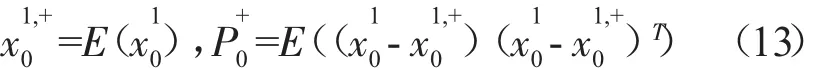
卡尔曼滤波器的迭代更新方程为

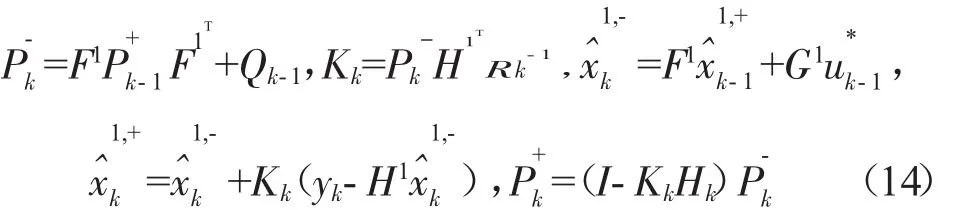
根据第2章建立的主燃油计量活门数学模型和本节建立的基于卡尔曼滤波算法的执行机构故障算法，可以得到仿真平台，如图11所示。

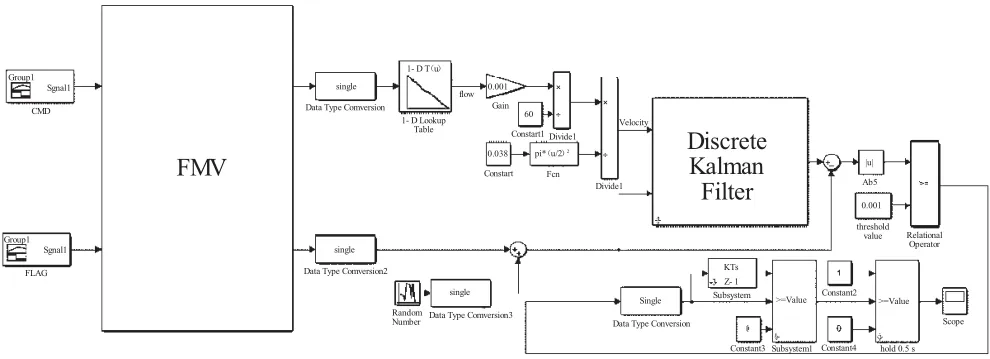
图11 主燃油计量活门故障诊断仿真平台

4 仿真结果

在本文讨论的卡尔曼滤波估计中，假设过程噪声很小，测量噪声较大，也就是噪声{vk}的方差Rk较大，使得式 (13)中计算的Kk值较小，在计算后验估计时，算法更加偏重于信任先验估计。总而言之，过程噪声{wk}的方差Qk和测量噪声{vk}的方差Rk更类似于加权系数，如果Qk较大（很大一部分原因是建模误差），那么认为卡尔曼滤波器更加偏重于信任测量输出，反之，则偏重于信任线性模型；如果Rk较大，那么认为卡尔曼滤波器更加偏重于信任线性模型，反之，则偏重于信任测量输出。

将第2章提取的主燃油计量活门线性模型与其非线性AMESim模型对比发现，建模误差较小，因此过程噪声较小，取为i=1…k；为了获得滤波效果较理想的值，而将测量噪声方差取得较大，将其分成4组进行测试

将4组测量噪声方差参数输入到仿真平台中，得到不同组别间的滤波效果，如图12所示。从图中可见，测量噪声方差越大，滤波效果越好，但噪声方差并不是越大越好，过大的测量噪声方差会使残差随故障注入的响应变慢，并且在一定程度上损失参数估计的鲁棒性。

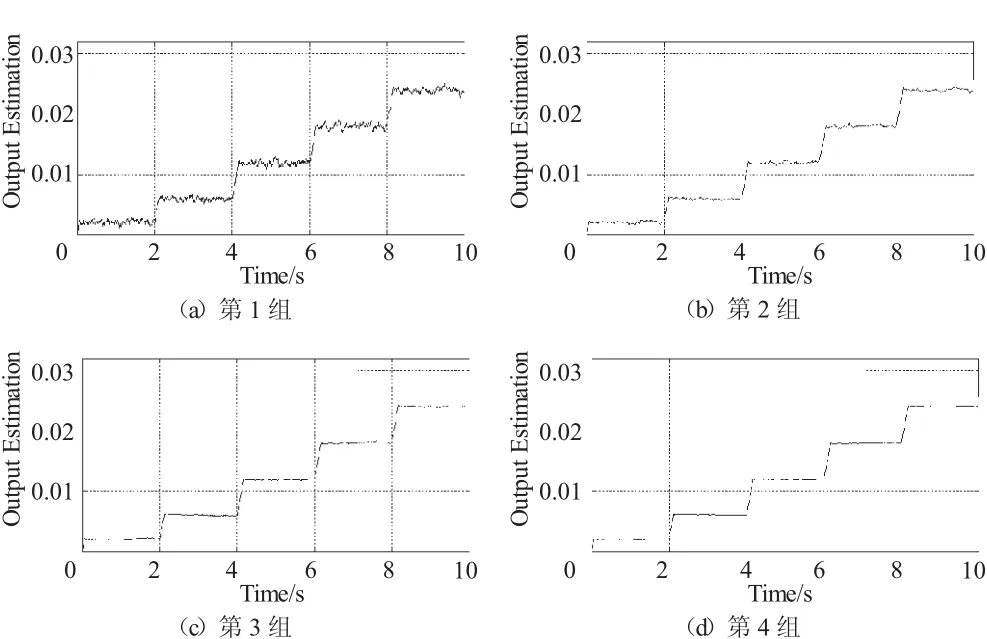
图12 测量噪声方差参数大小对滤波效果的影响

结合传感器输出，估计输出残差表达为

以电液伺服阀阀芯卡滞故障为例，在仿真时间的第5 s注入该故障，残差变化如图13所示。

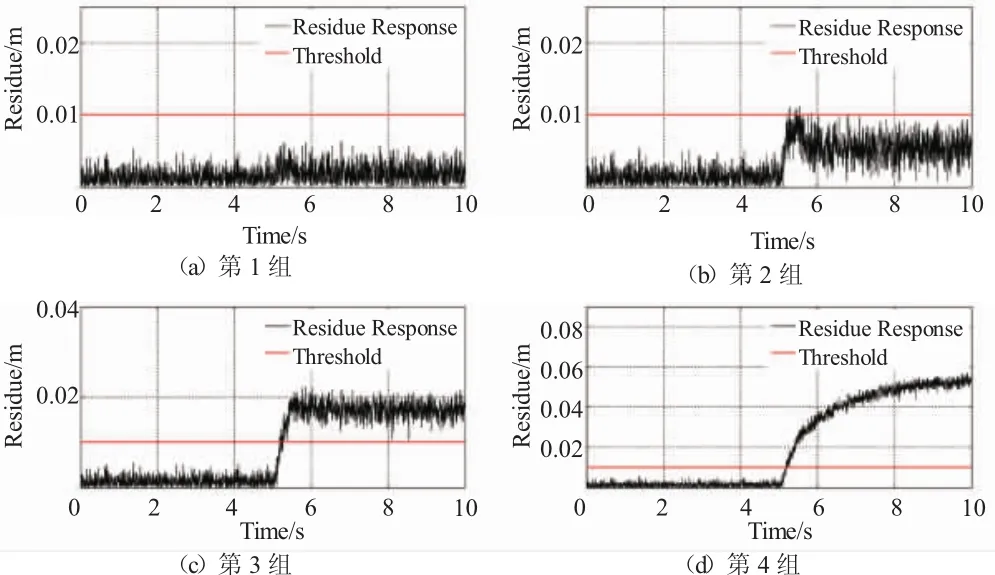
图13 残差响应变化

从图中可见，测量噪声方差增大使得估计输出残差幅值变大，也使估计输出残差响应变慢，过大的测量噪声参数会使卡尔曼滤波算法失去鲁棒性，综合考虑之下，取测量噪声方差为1000。5 s注入故障后，残差值迅速增加并超过报故阈值，从故障注入时刻到故障预警经历的时间为0.3 s，满足工程中对及时报警的要求，而在正常状态下，残差值远小于报故阈值，不会误报警。

目前，该故障诊断技术可以被用于电液执行机构控制回路故障诊断，包括电液伺服阀卡滞故障和漂移故障，以及作动筒燃油泄漏和作动筒活塞卡滞故障，对于以上故障都能诊断得到控制回路故障信号，接下来的工作将围绕阈值与故障类型之间的非线性映射关系展开研究。

5 结论

（1）主燃油计量活门的线性变参数（LPV）建模方法准确描述了原非线性系统，减小了建模误差，拓展了传统卡尔曼滤波器的应用范围。

（2）通过调整卡尔曼滤波器中的测量噪声方差和过程噪声方差，使得滤波效果明显。

（3）基于卡尔曼滤波器设计的残差生成器对故障很敏感，但对噪声和建模误差不敏感，残差的响应时间快，幅值较大，有效降低了故障误报警率和漏报警率。

[1]Kalman R E.A new approach to linear filtering and prediction problems[J].Journal of Basic Engineering,1960:35-45.

[2]Chinniah Y,Burtom R,Habibi S.Failure monitoring in a high performance hydrostatic actuation system using the Extended Kalman Filter[J].Mechatronics,2006（16）:643-653.

[3]WANG X,Syrmos V L.Fault detection,identification and estimation in the electro-hydraulic actuator system using EKF-based multiple-model estimation [C]//16thMediterranean Conference on Control and Automation Congress Centre,2008.

[4]An L,Sepehri N.Hydraulic actuator circuit fault detection using Extended Kalman Filter[C]//Proceeding of the American Control Conference,2003.

[5]An L,Sepehri N.Leakage fault identification in a hydraulic positioning system using Extended Kalman Filter[C]//Proceeding of the 2004 American Control Conference,2004.

[6]Kobayashi T,Simon D L.Intergration of on-line and off-line diagnostic algorithms for aircraft engine health management[C]//ASME Turbo Expo 2007:Power for Land,Sea and Air,2007.

[7]Kobayashi T,Simon D L,Hybrid K F.A new approach for aircraft engine in-flight diagnostics[R].Cleveland:National Aeronautics and Space Administration,2006.

[8]张东辉.航空发动机数控系统液压机械装置仿真研究[J].航空发动机，2012.38（2）:5-10.ZHANG Donghu.Simulation of Hydro-Mechanical Unit(HMU)for aeroengine digital control system[J].Aeroengine,2012,38（2）：5-10.（in chinese）

[9]Mccloy D,Martin H R.Control of fluid power：analysis and design[M].Ellis Horwood Limited,1980：68-71.

[10]刘大响，程荣辉.世界航空动力技术的现状及发展方向[J].北京航空航天大学学报，2002，28（5）：490-496.LIU Daxiang,Cheng Ronghui.Current status and development direction of aircraft power technology in the world[J].Journal of Beijing University of Aeronautics and Astronautics，2002，28（5）：490-496.（in Chinese）

[11]姚华，王国祥.航空发动机全权限数控系统研究和试飞验证[J].航空动力学报，2004，19（2）：247-253.YAO Hua,WANG Guoxiang.A study and flight evaluation of full authority digital engine control system[J].Journal of Aerospace Power，2004，19（2）：247-253.（in Chinese）

[12]张绍基.航空发动机控制系统的研发与展望 [J].航空动力学报，2004，19（3）：375-382.ZHANG Shaoji.A review of aeroengine control system[J].Journal of Aerospace Power，2004，19（3）：375-382.（in chinese）

[13]姚华，单贵平，孙建国.基于卡尔曼滤波器及神经网络的发动机故障诊断[J].航空动力学报，2008，23（6）：1111-1117.YAO Hua,SHAN Guiping,SUN Jianguo.Fault diagnosis for gas turbine engines based on Kalman filter and neural networks[J].Journal of Aerospace Power，2008，23（6）：1111-1117.（in Chinese）

[14]王施，王荣桥，陈志英，等.航空发动机健康管理综述[J].燃气涡轮试验与研究，2009，22（1）：51-59.WANG Shi，WANG Rongqiao，CHEN Zhiying， et al.Survey on aircraft engine health management[J].Gas Turbine Experiment and Research，2009，22（1）：51-59.（in Chinese）

[15]王世元.非线性卡尔曼滤波器原理及应用 [M].电子工业出版社，2015：12-17.WANG Shiyuan.Principles of nonlinear Kalman filters and their applications[M].Beijing:Publishing House of Electronics Industry，2015，12-17.（in Chinese）

Fault Diagnosis of Main Fuel Metering Device Based on Kalman Filter

LU Hai-yang1，2，WANG Xi1，2
（1.School of Energy and Power Engineering，Beihang University，Beijing 100191，China；2.Collaborative Innovation Center for Advanced Aero-Engine，Beijing 100191，China）

In order to establish the fault diagnosis algorithm of the main fuel metering Electro Hydraulic Actuator(EHA),the working principle of the main fuel metering device was analyzed,a method of establishing the main fuel metering Linear-Parameter-Varying （LPV）model was presented and finally residual generator main fuel metering Electro Hydraulic Actuator's displacement output was designed based on discrete Kalman filter.Simulation results show that the residual generator is sensitive to fault and insensitive to noise and modeling errors,the dynamic response of the residual is fast,the change of the amplitude of the residual error is large,the false alarm rate and missing alarm rate are reduced effectively.

main fuel metering device;fault diagnosis;Kalman filter;actuator；linear model

V 233.7+53

A

1 0.1 3477/j.cnki.aeroengine.201 7.02.004

2016-10-28

芦海洋（1991），男，在读硕士研究生，主要研究方向为航空发动机燃油控制系统建模及故障诊断；E-mail：1334249649@qq.com。

芦海洋,王曦.基于卡尔曼滤波器的主燃油计量装置故障诊断[J].航空发动机，2017，43（2）：17-22.LU Haiyang，WANG Xi.Faultdiagnosis ofmain fuelmetering device based on Kalman filter[J].Aeroengine，2017，43（2）：17-22.

（编辑：赵明菁）