含振动能激发Boltzmann模型方程气体动理论统一算法验证与分析∗
彭傲平李志辉 吴俊林蒋新宇
1)(中国空气动力研究与发展中心,超高速空气动力研究所,绵阳 621000)2)(中国空气动力研究与发展中心,空气动力学国家重点实验室,绵阳 621000)3)(国家计算流体力学实验室,北京 100191)
含振动能激发Boltzmann模型方程气体动理论统一算法验证与分析∗
彭傲平1)李志辉1)2)3)†吴俊林1)蒋新宇1)
1)(中国空气动力研究与发展中心,超高速空气动力研究所,绵阳 621000)2)(中国空气动力研究与发展中心,空气动力学国家重点实验室,绵阳 621000)3)(国家计算流体力学实验室,北京 100191)
振动能激发,Boltzmann方程,气体动理论统一算法,热力学非平衡效应
为模拟研究高温高马赫数下多原子气体内能激发对跨流域非平衡流动的影响,将转动能、振动能分别作为气体分子速度分布函数的自变量,把转动能和振动能处理为连续分布的能量模式,将Boltzmann方程的碰撞项分解成弹性碰撞项和非弹性碰撞项,同时将非弹性碰撞按一定松弛速率分解为平动-转动能松弛过程和平动-转动-振动能松弛过程,构造了一类考虑振动能激发的Boltzmann模型方程,并证明了其守恒性和H定理.基于内部能量变量对分布函数无穷积分,引入三个约化速度分布函数,得到一组考虑振动能激发的约化速度分布函数控制方程组,使用离散速度坐标法,基于LU-SGS隐式格式和有限体积法求解离散速度分布函数,建立含振动能激发的气体动理论统一算法.通过开展高稀薄流到连续流圆柱绕流问题统一算法与直接模拟蒙特卡罗法模拟结果对比分析,特别是过渡流区平动、转动、振动非平衡效应对绕流流场与物面力热特性的影响机制,证实了所建立的含振动能激发的Boltzmann模型方程及气体动理论统一算法的准确可靠性.
1 引 言
航天器从外层空间再入大气层跨流域高超声速、高温绕流流场中,气体分子的微观自由度(平动、转动、振动和电子态)因受到一定程度的激励,会出现能量彼此传递,使分子和原子间发生化学和电离反应[1].气体的宏观运动和状态变化同相应的微观物理化学过程相互影响呈现复杂的非平衡现象.根据表征分子微观自由度之间能量传递或组元之间进行化学反应的特征弛豫时间与流动特征时间大小尺度的不同,可将非平衡流动分为平动和转动非平衡流、振动和化学非平衡流以及电离辐射非平衡流[2].如果流动特征时间极小或流场的物理量变化梯度极大,平动、转动与振动非平衡效应表现为与分子性质相关联的气体介质特性,如比热、比热比等不再保持常数,出现黏性、热传导和扩散的非平衡变化,这是一种最基本且接近高超声速再入多尺度非平衡流动的现实环境.在统计热力学研究中,一个气体分子的总能量是平动能、转动能、振动能、电子能等几种能量模式的总和,由于电子能模式过于复杂,已不能采用几何和热自由度来描述,且电子能激发需要大量能量,对于大部分气体分子而言,在电子激发前分子结构就已经被破坏,通常在不太高的温度下电子能一般不会激发,可忽略不计.所以在后面的讨论中,我们假设分子只具有三种能量模态:平动能、转动能和振动能.
对于不考虑内能影响的简单气体,仅有平动能,气体分子运动论(气体动理学理论)的基本方程——Boltzmann方程[3−8]能很好地描述从连续流到自由分子流各个流动区域的气体分子输运现象,该方程是一个高度非线性积分-微分方程,除Maxwell分布等少数几个解析解外,几乎不可能求出精确解.为此简化而来的Bhatnagar-Gross-Krook(BGK)模型方程[9]、椭球统计模型方程[10],Shakhov模型方程[11]等能较好地用于简单气体流动现象的模拟,这些模型方程结构简单、便于数值模拟[12−19],特别是近十余年,文献[13,16,19—27]从分析研究气体分子速度分布函数与宏观流动量变化关系出发,使用气体分子碰撞松弛参数和当地平衡态分布函数,对Boltzmann方程碰撞积分进行物理分析与可计算建模,确立描述各流域复杂流动输运现象统一的Boltzmann模型方程,提出并发展了可用于高、低不同马赫数绕流模拟的离散速度坐标法与动态确定物理空间宏观流动量的离散速度数值积分技术,先后建立起求解跨流域绕流问题的气体动理论统一算法(GKUA)与航天器再入跨流域多尺度绕流气动力/热问题并行计算应用研究平台[19,28].在针对航天器试验与飞行状态的气动特性研究中,气体介质均为双原子气体或者多原子气体,随着温度的增加气体分子内能的激发将会对其输运系数、飞行器绕流流场参数的分布产生影响,尤其是航天器再入过程中,因高温高速引起的气体振动能激发等现象显著,为数值模拟研究这种非平衡流动问题,在连续流区域通常采用基于多温度模型的N-S方程[29,30]、稀薄流区采用基于Larsen-Bergnakke唯象论模型的直接模拟蒙特卡罗法(DSMC)方法[31−33],而过渡流区尚未有准确可靠的非平衡流动模拟方法.
根据Boltzmann方程描述气体流动过程中微观分子速度分布函数基于位置空间、速度空间在任一时刻由非平衡态向平衡态的演化属性,可以考虑从其出发进行模型化设计,研究全流域尤其是过渡流区的非平衡流动问题.为此,Wang等[34,35]提出了一种处理具有内能影响的多原子气体的半经典方法,即平动能根据自由度按经典方法处理,而内自由度按量子力学观点处理,由此得到了Boltzmann方程的推广形式——王承书-乌伦贝克(WCU)方程,该方程在分子内能为非简并态时成立.Morse[36]在Wang等研究成果的基础上,将弹性碰撞与非弹性碰撞解耦用于处理能量松弛过程,依此构造了一种类似BGK模型的考虑分子内能间断能级的模型方程.在这些研究中,内能是作为单一模式处理的,即没有区分转动能和振动能.如果按量子力学观点处理分子能级的跃迁,每个能级均为一个独立的分布函数,势必会加大数值处理的难度.尽管在高温下分子结构具有量子效应,但在实际的气体流动中其量子效应是可以忽略的[4],因此可以将分子的内能态看成是连续的,可采用经典热力学的方法进行处理.根据这种思想建立的双原子气体ES-BGK模型[10,37,38]、Rykov模型[39−42]等仅考虑了转动能的影响.但随着温度的进一步增加,振动能开始激发,其对气体热力学特性的影响将越来越明显,例如对空气而言当温度超过600 K时振动能的影响将不可忽略.Holway[10]在Morse研究的基础上,将内能中的转动能和振动能分别按经典方法和间断能级处理,建立了适于多原子气体的ES模型.Tantos等[43,44]根据量子效应是可以忽略的思想[4,45]对多原子气体ES模型进行改造后用于平板间热传导研究,考察了气体转动能、振动能激发对热传导的影响.
本文根据连续能级的处理方式,在文献[46—48]开展双原子气体含转动非平衡效应Boltzmann模型方程统一算法研究的基础上,将转动能、振动能分别作为气体分子速度分布函数中的自变量,引入转动能、振动能能模,将Boltzmann方程的碰撞项分解成弹性碰撞项和非弹性碰撞项两部分,同时根据Holway[10]处理碰撞过程中能量松弛的思想,将非弹性碰撞项按一定的松弛速率分解为平动-转动能松弛和平动-转动-振动能松弛,构造一类考虑振动能激发的Boltzmann模型方程.为数值求解该模型方程,引入三个约化速度分布函数,得到一组考虑振动能激发的约化速度分布函数控制方程组,在气体动理论统一算法[19−28]体系下,使用离散速度坐标法,结合LU-SGS隐式格式和有限体积法对约化速度分布函数控制方程组进行求解[26,27],捕捉离散速度分布函数演化更新,拟研究建立含振动能激发的气体动理论统一算法.以圆柱绕流问题为研究对象通过开展稀薄流到连续流区统一算法与DSMC方法结果对比分析,特别是过渡流区平动、转动、振动非平衡效应对绕流流场与物面力热特性的影响机制,对所建立的含振动能激发的Boltzmann模型方程进行验证分析.
2 建立含振动能激发的Boltzmann模型方程
2.1 气体分子速度分布函数对宏观流动量的动态表征关系
在不考虑气体离解和化学反应的情况下,引入转动能和振动能的气体分子速度分布函数可定义为f(r,ξ,t;erot,evib),其中t为时间,r为空间位置坐标,ξ为分子运动速度;erot,evib分别为转动能和振动能能模,在量子态下为对应的各个能级能量值,这里将其视为连续能级中的点,取值范围均为[0,+∞),并假定二者为相互独立的变量.宏观流动量可以通过对分布函数取矩的方法得到[20,21,24,49,50].设nrot,vib为能模erot,evib下的数密度,nvib为能模evib下的数密度,n为气体流动当地数密度,U为宏观气体流动速度;Ttr,Trot,Tvib分别为平动、转动和振动温度;qtr,qrot,qvib分别为分子平动、转动和振动能输运产生的热流矢量,而总的热流矢量qtot为三者之和;τij为胁强张量在i,j方向的分量;p为流场压力.则各宏观流动量的表达式为


i,j对应x,y,z,p=nkBTtr,qtot=qtr+qrot+qvib,其中,m为分子质量;δrot,δvib分别为气体分子的转动和振动自由度;kB为Boltzmann常数;C=ξ−U为分子随机热运动速度.
由于气体的转动特征温度Θrot很低(如O2为2.07 K,N2为2.88 K),因而在实际的气体动力学研究领域可以认为分子的转动能是完全激发的,转动自由度δrot可以确定,对于线性分子如O2,N2,CO2等,δrot=2,对于非线性分子如H2O等,δrot=3.而振动特征温度Θvib较高(如O2为2256 K,N2为3371 K,CO2有三个,分别为960,1930,3390 K),一般情况下振动能难以完全激发,其自由度δvib为温度的函数,假设分子具有N个振动特征温度即N个振动模式,对于线性分子N=3M−5,对于非线性分子N=3M−6,这里M为分子中的原子个数,则温度T时总的振动自由度为

其中,Θv,i为第i振动能模式下的振动特征温度.
在分布函数中引入转动能和振动能能模后,需要首先确定平衡态时的分布函数fM.文献[3,4]中给出了转动能和振动能能模的分布函数为


结合麦克斯韦速度分布函数,则有[51]
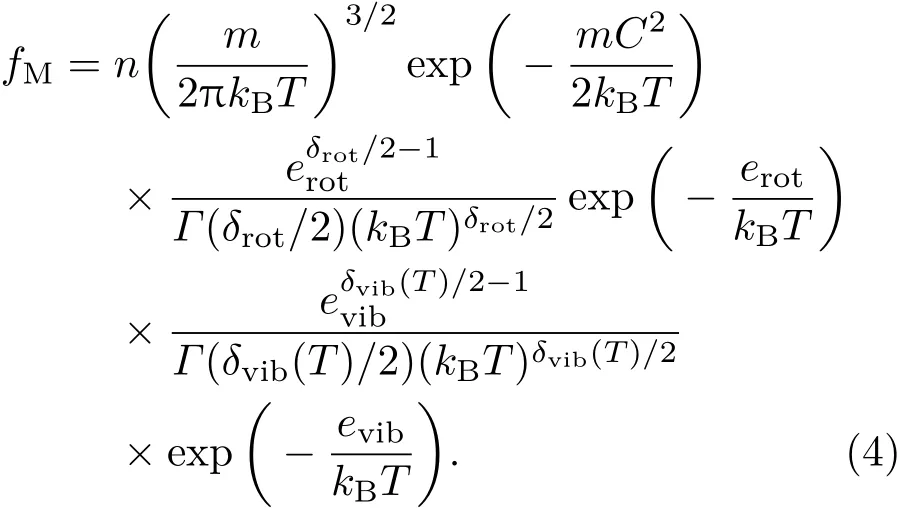
同时定义平动-转动实效温度Tt,r和平动-转动-振动实效温度Tov(即流场等效温度)分别为

(5)式中,Tov可通过迭代的方法进行求解.
在实效温度的定义中引入了平动温度Ttr、转动温度Trot和振动温度Tvib这三种温度,因此可以建立一种考虑振动能激发的三温度Boltzmann模型方程.参照现有多原子气体动力学模型方程如Rykov等[39−41]模型方程,Holway[10]的间断能级模型方程等的构造原理,将分子运动的松弛过程简化为平动能松弛、平动-转动能松弛和平动-转动-振动能松弛,而忽略转动能间、振动能间以及转动-振动能间等的松弛.由此可以将Boltzmann模型方程写成如下形式:

其中,


这里,υtot=Pr·nkBTtr/µ,Zrot和Zvib分别为转动和振动松弛碰撞数,Pr为气体Prandtl数,µ为黏性系数.在DSMC方法中,通常取但是在动理学模型方程中,需要通过温度的松弛过程来确定其中的松弛碰撞数.在实际计算中通常取

由于分布函数f(r,ξ,t;erot,evib)中包含了ξ,erot,evib,如果对这几个变量均采用离散坐标法,计算量将很大,为此引入如下三个约化速度分布函数:
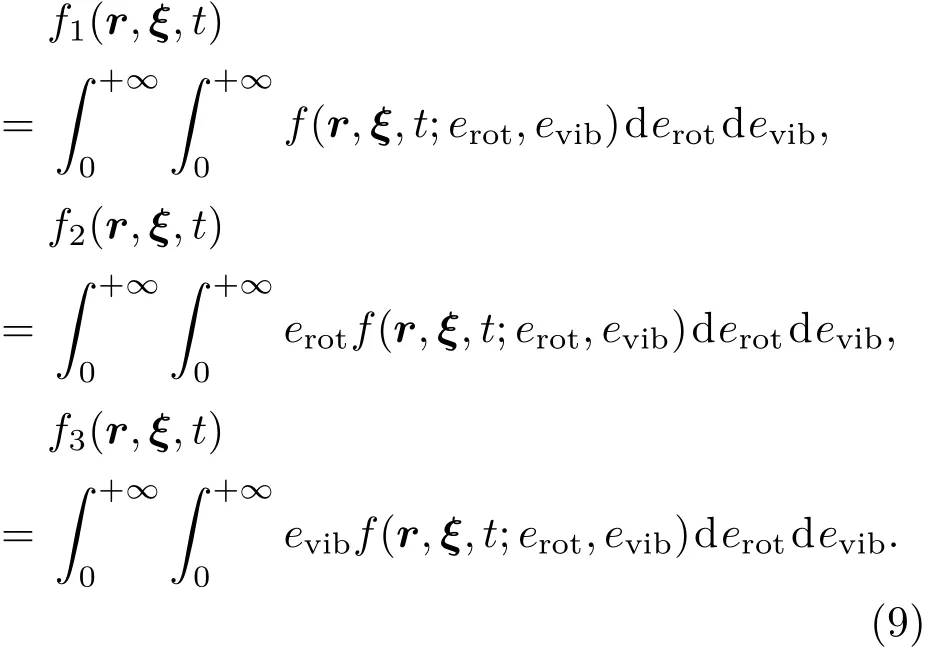
代入方程(6),有

其中,i=1,2,3,且有
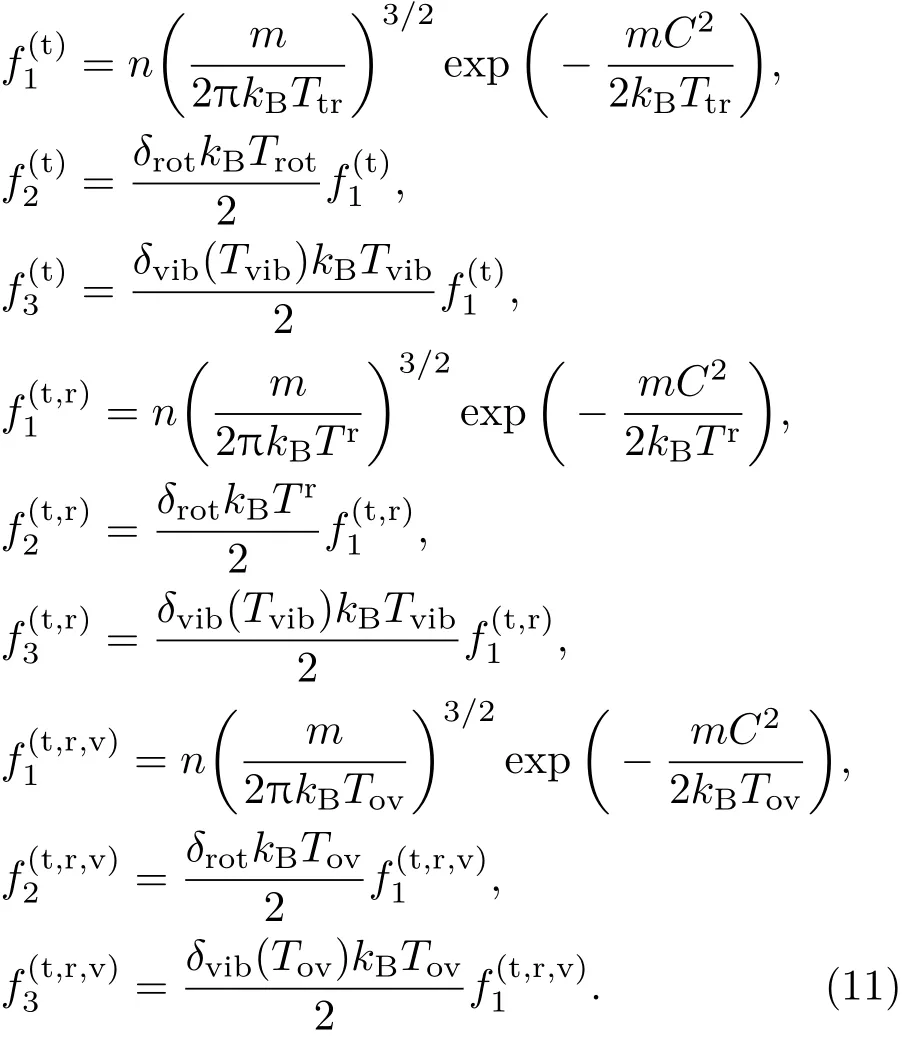
则任意时刻三个约化速度分布函数对宏观流动量的表示式为:

为数值求解方便,引入如下无量纲参数将气体动力学模型方程进行无量纲化:
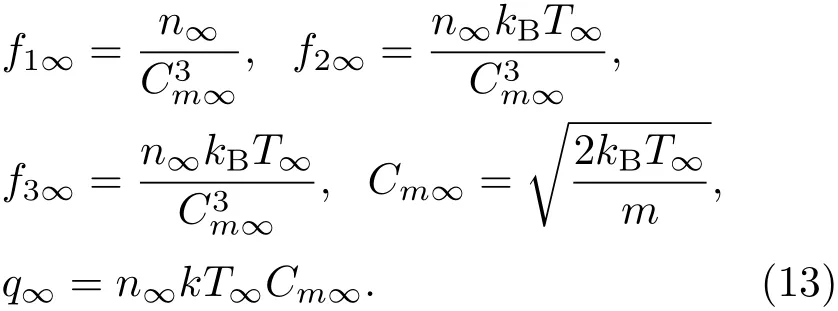
则控制方程可写为
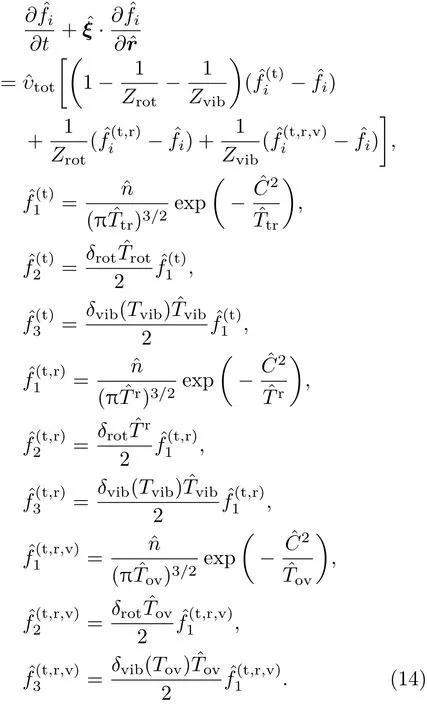
宏观流动量的表达式可写为:
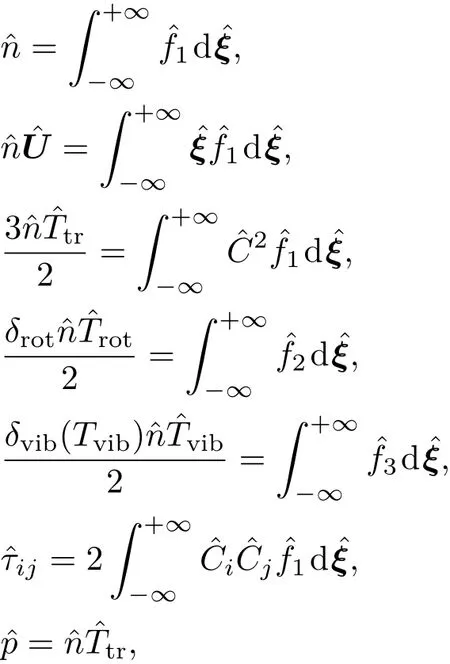

2.2 守恒性及H定理的证明
在确定气体动理学模型方程后需要对其基本属性进行分析,这里考虑无量纲后的方程,并省略顶标 “ˆ”. 首先设

这里,υrot=υtot/Zrot,υvib=υtot/Zvib. 则由质量、动量和动能守恒关系,有

由于


则可知(17)式前两项自动满足,同时可得
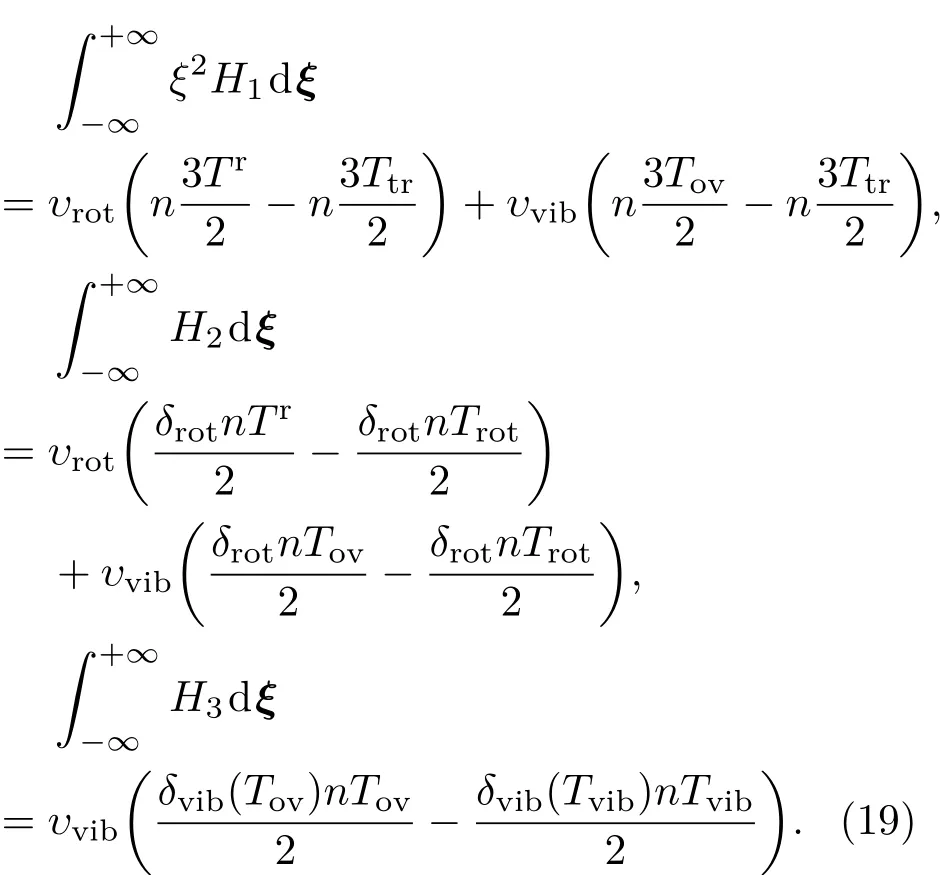
代入(17)式第三项得

则
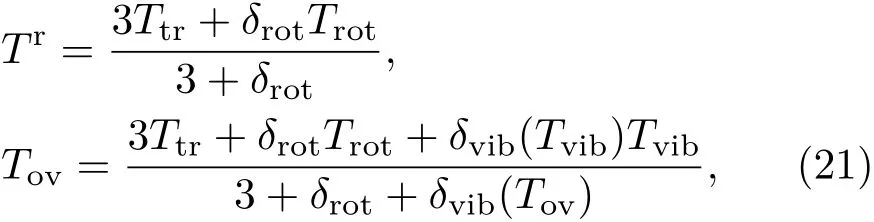
与(5)式一致,说明(5)式的定义是合理的,满足能量守恒.
由Boltzmann方程的H定理可知,气体动理学模型方程碰撞项Hi应满足

对于i=1的情形,假设υtr=υtot− υrot−υvib,(22)式变为
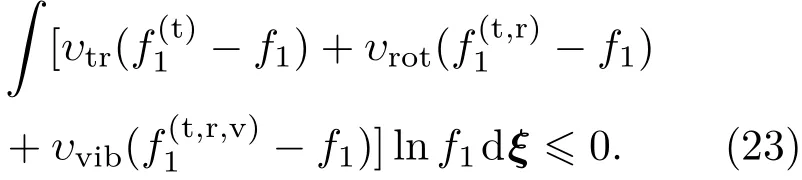
由于

而


由于υtr,υrot,υvib均大于零,当f1,不同号时(26)式右边第一项的被积函数小于零,其积分值也应小于零,同样当f1与分别不同号时(26)式右边第二项、第三项均小于零,当且仅当时(26)式等于零,即(23)式成立.
对于i=2和3的情形可类似得到.于是该动理学模型方程的H定理得以证明.
2.3 物面边界条件的可计算建模
在物面边界上,气体分子从物面反射进入气流,假定物面对分子没有吸附作用,且反射是瞬时完成的,反射分子按完全漫反射处理,即以完全适应于物面温度Tw和速度Uw的平衡态分布散射,其分布函数为

约化后的速度分布函数为

其中,Cw=ξ−Uw,对于固定物面,Uw=0,nw为物面数密度.沿物面法线方向,流体质量流量为零,有
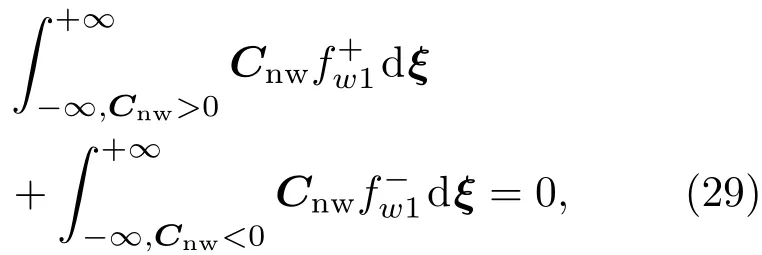
可得出经物面反射的气体分子数密度nw,其中,Cnw=Cw·vwall,vwall为物面单位外法向矢量,由物面指向流体内部.可由内场分布函数插值得到.
3 构造含振动能激发的Boltzmann模型方程隐式格式
在确定气体动理学模型方程和物面边界条件后,可采用离散速度坐标法、LU-SGS隐式格式和有限体积法进行求解[25−27].
以二维气体流动为例,经离散速度坐标法在离散速度点(ξxσ,ξyδ)处对速度空间离散降维的Boltzmann模型方程一般式可写为

其中,σ,δ为离散速度网格点,Sυσ,δ为控制方程右手项.
在采用有限体积法求解上述方程时,首先在网格中心型单元控制体积ΩIJ内积分,有
1.PERT指征:临床确诊或疑诊PEI,即可行PERT[1]。可根据患者基础疾病、PEI临床症状、胰腺外分泌功能检测、营养不良的客观证据等进行综合评估。

其中,F=(ξxσfσ,δ)i+(ξyδfσ,δ)j,v为单元控制体边界沿位置空间网格I,J增大方向的法向量,符号表示量XIJ在控制体积ΩIJ内的平均值.
根据积分变换原则,(31)式左边第二项可以改写为:

这里,A=∂F∂f=(ξx)i+(ξy)j.
利用Steger-Warming流通矢量分裂,将控制体积界面上的通量分解为正通量和负通量,其中正通量由计算得出,负通量由计算得出,即


最终控制方程可以写成
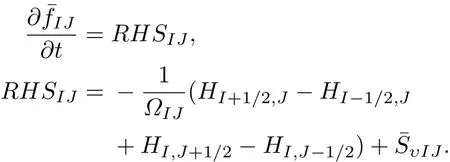
若采用显式格式,上式可由二阶或三阶具有TVD性质的Runge-Kutta方法计算[23−27,30].为提高计算效率本文基于LU-SGS计算原理,构造求解Boltzmann模型方程的隐式方法.根据隐式格式构造原理,推导后有

由于网格中心型有限体积法所得到的分布函数位于控制体中心,因此物面分布函数应首先通过靠近物面若干排控制体中心分布函数插值得到,再通过物面质量流量为零和物面分子反射后按Maxwell分布的原则对物面分布函数进行修正,进而得到物面上各个宏观绕流参数.
4 算法验证与结果分析
为了考察直接求解Boltzmann模型方程气体动理论统一算法对稀薄流到连续流跨流域气体流动问题模拟能力与准确收敛性,拟定来流马赫数Ma∞=1.8、克努森数分别为Kn∞=0.3与Kn∞=0.0001的两组圆柱绕流状态,图1(a)绘出了本文统一算法对高稀薄圆柱绕流Kn∞=0.3流场沿驻点线密度分布计算结果与DSMC模拟值的比较情况.由图可见,两种结果符合较好,GKUA计算结果光滑稳定,与DSMC模拟变化规律一致.图1(b)展示了Kn∞=0.0001连续介质流动状态下圆柱绕流流场物面压力分布GKUA计算结果与连续介质流理论的经典分析数据比较情况,其中符号“□”表示GKUA计算结果,符号“Δ”为取自文献[20]引用的连续流理论解经典数据,可看出二者整体上符合较好.这检验了直接求解Boltzmann模型方程的GKUA在计算高稀薄流到连续流区绕流状态正确性.只是在偏离驻点较远位置,存在一定的系统偏差,这可能是由于文献[20]数据是由完全连续介质流理论得到,而本文GKUA计算是以Kn∞=0.0001作为连续介质流动状态参与比较,而真实连续流是克努森数趋于零所对应的流动状态.
为考察本文所建立的含振动能激发Boltzmann模型方程及其在气体动理论统一算法中实现的正确可靠性,拟定非平衡效应严重的稀薄过渡流区圆柱绕流问题进行统一算法计算检验,并与DSMC方法结果对比分析.所有DSMC方法的结果均由Bird[52]的DS2V软件模拟而得到.设置来流气体为N2,Ma∞=5,T∞=Tw=500 K,Kn∞=0.01.图2绘出了本文含振动能激发的Boltzmann模型方程统一算法计算结果(图中用“GKUA_vibration”表示)与DSMC方法结果(图中用“DSMC”表示)的对比情况.从图2中可以看出,两者激波位置略有差别,这是由于DSMC方法采用的是自适应的非结构网格,在宏观流动量梯度大的位置进行了自适应加密,可以更好地捕捉激波,而本文GKUA采用的是近物面加密的结构网格,在激波位置网格稍宽,对激波的捕捉能力稍弱,进一步研究可通过加密网格得到更好的结果,但会增加计算开销.从宏观流动量的分布云图来看,两种结果符合较好,压力和等效温度分布几乎完全一致,表明本文建立的考虑振动能激发的Boltzmann模型方程是合理可行的.从平动、转动、振动温度的分布来看,在波后驻点区域,平动温度最高,转动温度次之,振动温度最低,本文计算所得的振动温度略高于DSMC方法的结果.
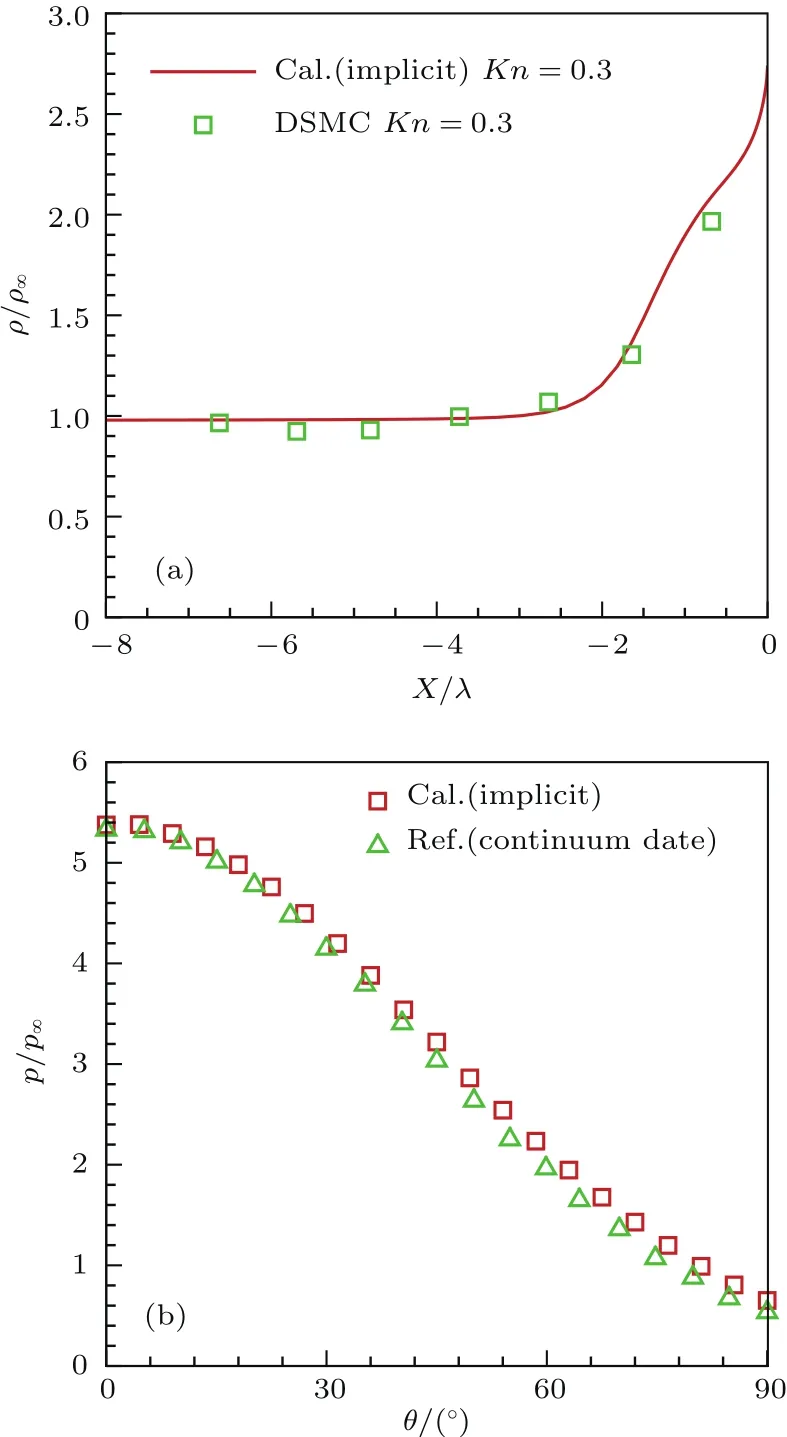
图1 跨流域圆柱绕流流场与物面压力分布GKUA计算与DSMC、连续流经典数据比较验证 (a)Kn∞ =0.3时驻点线密度分布;(b)Kn∞=0.0001时沿物面迎风面压力分布Fig.1.Validation of fl ow fi eld and surface pressure distribution of Ma∞=1.8 around cylinder covering fl ow regimes with comparison of GKUA,DSMC and classical data of continuum fl ow:(a)Stagnation line density distribution for Kn∞=0.3;(b)wind-surface pressure distribution for Kn∞=0.0001.
对于多原子气体,在不考虑离解等化学反应的情况下,气体分子除具有平动能外,还具有内能,即转动能和振动能.气体的转动特征温度很低(一般小于10 K),一般情况下转动能完全激发,而振动特征温度较高,振动能随温度升高逐渐激发.对于N2而言,其振动特征温度为3371 K,当温度大于750 K时其振动自由度大于0.1,振动能激发的影响开始显现.从图2中各种温度分布来看,波后绝大部分区域内温度都高于750 K,内能激发将会对流场结构产生影响,图3(a)—图3(c)给出了GKUA基于简单气体的Shakhov模型计算结果(图中用“GKUA_Shakhov”表示)与本文考虑振动能激发的Boltzmann模型方程统一算法结果(图中用“GKUA_vibration”表示)的对比情况.在考虑内能激发后,激波更贴近物面,气体分子一部分平动能转化成内能,使得平动温度明显降低,同时可以看出基于简单气体Shakhov模型的统一算法结果的激波角略大于考虑内能激发后的结果.图3(d)—图3(f)给出了仅考虑转动能激发的多原子气体ES模型统一算法(图中用“GKUA_ES”表示)与本文考虑振动能激发的计算结果(图中用“GKUA_vibration”表示)的对比情况.可以看出,两种途径得到的宏观流动量等值线云图基本相同,但基于ES模型的GKUA计算所得的平动温度和转动温度在波后要高于考虑振动能激发的统一算法结果,说明气体分子的部分能量转化成振动能使得温度降低.图3直观清晰地展示了振动激发对流场结果的影响.

图2 (网刊彩色)本文含振动能激发的Boltzmann模型方程GKUA计算所得宏观流动量与DSMC方法结果对比(a)马赫数;(b)压力;(c)等效温度;(d)平动温度;(e)转动温度;(f)振动温度Fig.2.(color online)Macro-parameters simulated in present method comparing with DSMC method:(a)Mach number;(b)pressure;(c)overall temperature;(d)translational temperature;(e)rotational temperature;(f)vibrational temperature.

图3 (网刊彩色)本文含振动能激发的Boltzmann模型方程GKUA计算所得宏观流动量分别与简单气体Shakhov模型、多原子气体含转动能激发ES模型的GKUA结果对比 (a)马赫数;(b)压力;(c)平动温度;(d)马赫数;(e)平动温度;(f)转动温度Fig.3.(color online)Macroscopic fl ow variables simulated by the present GKUA with comparison of Shakhov model and ES model:(a)Mach number;(b)pressure;(c)translational temperature;(d)Mach number;(e)translational temperature;(f)rotational temperature.
图4给出了分别考虑平动、转动、振动不同非平衡效应,使用本文GKUA与DSMC计算所得的物面热流与压力分布曲线对比情况,其中“GKUA-Shakhov”表示将N2作为简单气体采用基于Shakhov模型的GKUA计算结果,“GKUA-ES”表示仅考虑转动能激发而基于多原子气体ES模型的GKUA计算结果,“GKUA-vibration”表示考虑N2振动能激发的本文Boltzmann模型方程GKUA所得结果,“DSMC-translation”表示将N2作为简单气体不考虑内能激发的DSMC结果,“DSMC-rotation”表示仅考虑N2转动能影响的DSMC结果,“DSMC-vibration”表示考虑N2振动能激发的DSMC结果.从图4(a)所示物面热流分布曲线可以看出,在驻点附近,“DSMC-translation”结果明显高于其他几种结果,且存在严重的统计波动,在绕流圆柱物面中部,“GKUA-vibration”偏离其他几种结果,最大偏差不超过15%.而图4(b)所示物面压力分布曲线显示在驻点附近“DSMC-translation”结果最小,“GKUA-Shakhov”次之,其他结果几乎重合.表1给出了不同非平衡效应内能激发的Boltzmann模型方程统一算法与DSMC方法模拟得到的圆柱气动力系数对比情况,从中可以看出,相较于简单气体模型,分别考虑转动、振动能影响的Boltzmann模型方程GKUA所得轴向力系数与法向力系数均有所增大,但幅度在2.5%以内,说明内能激发对气动力系数影响很小.

图4 (网刊彩色)不同非平衡效应不同方法模型计算得到的物面热流和压力分布 (a)热流;(b)压力Fig.4.(color online)Heat fl ux and pressure on the wall with different non-equilibrium e ff ects and method models:(a)Heat fl ux;(b)pressure.

表1 不同气体模型GKUA算法与DSMC方法所得的轴向力系数和法向力系数对比Table 1.Axial force coefficients and normal force coefficients of cylinder by different gas models comparing GKUA method with DSMC method.
根据上述结果分析,由于物面温度设置为500 K,较N2的振动特征温度3371 K低很多,不足以使与物面发生碰撞的气体分子振动能大量激发,因此尽管动理学模型方程中考虑了振动能的激发,但对与物面相关的气动力系数、物面热流分布等影响很小,在流场内部尤其是激波后的核心区域,温度很高,足以引起振动能的激发,导致流场参数与流动结构发生明显变化.
为了进一步分析内能激发、振动特征温度高低不同对绕流的影响,这里假设N2的振动特征温度为500 K,而其他条件不变,使用GKUA计算上述同一状态,得到的圆柱绕流轴向力系数为0.7043、法向力系数为0.4061.对比表1中振动能一行,可以看出,即使把振动特征温度设置更低为500 K,气体分子振动能激发更为明显时,所计算的轴向、法向气动力系数仅由0.7044,0.4063降低为0.7043,0.4061,几乎没有变化,可以认为在计算误差范围内,其变化幅度为0.049%.进一步分析表1表明,分别使用GKUA与DSMC计算得到的结果偏差范围0.06%—1.67%,证实两种方法各自计算实现的正确性,同时可以看出从简单气体到转动能再到振动能影响,所带来的轴向力、法向力系数相对变化量在1.97%—2.97%.图5绘出了设置不同振动特征温度Θvib=500 K与Θvib=3371 K条件下,GKUA计算的流场中平动温度、转动温度、振动温度和等效温度分布等值线云图对比情况.由图5可看出,各图上半部分若设置振动特征温度Θvib=500 K较小时,气体分子的振动能激发在较低温度时发生,振动非平衡效应过于明显,需要消耗更多气体流动能量,使得流场内部的温度偏低.尤其是在激波后的核心区域,温度接近2500 K,以Θvib=500 K计则振动自由度达到1.81,而实际Θvib=3371 K对应的振动自由度为0.946,前者接近完全激发,从图5(c)和图5(d)可以看出,内能完全激发,分别在上述两个振动特征温度设置下GKUA计算振动能显著激发后的绕流物体周围的温度分布呈现明显变化.
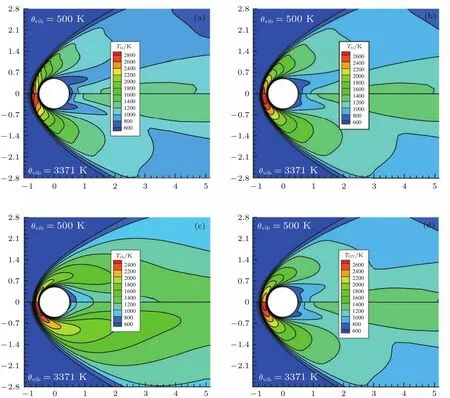
图5 (网刊彩色)不同振动特征温度设置下圆柱绕流流场温度等值线云图 (a)平动温度;(b)转动温度;(c)振动温度;(d)等效温度Fig.5.(color online)Temperature distribution in the fl ow fi eld with different sets of characteristic temperature of vibration:(a)Translational temperature;(b)rotational temperature;(c)vibrational temperature;(d)overall temperature.
图6给出了上述两种振动特征温度设置下圆柱绕流物面热流和压力分布.由于物面温度保持为500 K,若设置Θvib=500 K所对应的振动自由度为1.164,而实际振动特征温度Θvib=3371 K时振动自由度仅为0.016.从图中可以看出,随着振动特征温度的降低,振动能的激发对驻点区域的热流和压力影响非常明显,其中驻点热流降低了约15%,压力降低约8%.结合图4对分别考虑平动、转动、振动非平衡效应所得到物面热流与压力分布的对比分析,可以推测,当物面温度增加时,即使振动特征温度较高,也会对物面的热流和压力分布产生影响.

图6 (网刊彩色)不同振动特征温度设置下圆柱绕流物面热流和压力分布 (a)热流;(b)压力Fig.6.(color online)Heat fl ux and pressure along the wall surface with different sets of characteristic temperature of vibration:(a)Heat fl ux;(b)pressure.
5 结 论
根据表征分子微观自由度之间能量传递的特征弛豫时间与流动特征时间大小尺度的不同与气体分子碰撞过程能量松弛演化特点,将Boltzmann方程的碰撞项分解成弹性碰撞项和非弹性碰撞项两部分,并将非弹性碰撞项按一定松弛速率分解为平动-转动能松弛和平动-转动-振动能松弛过程,将转动能、振动能分别作为气体分子速度分布函数的自变量,把转动能和振动能处理为连续分布的能量模式,构造了一类考虑振动能激发的Boltzmann模型方程,并证明了其守恒性和H定理.通过对稀薄流到连续流跨流域圆柱绕流问题Boltzmann模型方程统一算法模拟验证与过渡流区考虑平动、转动与振动能激发的圆柱绕流模拟,得出以下结论.
1)通过将相同状态下本文统一算法结果与DSMC方法结果对比,两者符合较好,验证了本文建立的含振动能激发的非平衡Boltzmann模型方程是准确可靠的.
2)通过对简单气体、仅考虑转动能激发的气体以及考虑振动能激发的气体圆柱绕流进行模拟,研究发现内能激发对流场参数分布影响较大,激波位置更贴近物面,而温度的分布变化最为显著,激波后核心区的温度因能量转化使振动能激发而有所下降.分子内能激发热力学非平衡效应的实质是平动能向转动能、振动能的传递以及各个能量间的交换,而根据经典热力学的原理,能量的宏观表现为温度,气体分子各个能量间的传递达到平衡时,必然会导致宏观温度的降低.
3)考虑分子内能激发后,相比简单气体,气动力系数会小幅增加,但即使气体分子振动能几乎完全激发,影响也较小.气动力的微观本质为气体分子与物面碰撞引起的动量变化,宏观上为应力张量在法向、切向作用的体现,而在能量松弛过程中平动能间的松弛时间比其他几种要短得多,导致内能的激发对应力张量的变化影响较小,正应力和切应力小幅增加.
4)当物面上气体分子的振动能激发显著增加时,驻点区域物面压力和热流会出现较为明显的下降.压力是通过平动温度计算,而热流为温度梯度的变化,对于等温物面,在驻点附近温度最高,内能的激发更为显著,平动能降低导致平动温度降低,进而压力较小,内能激发导致驻点区域等效温度降低,温度梯度也随之降低,热流也减小.
本文仅是含内能激发热力学非平衡效应Boltzmann模型方程数值算法的初步工作与阶段成果,下一步将开展更多状态尤其是高马赫数的模拟研究,并拓展到三维问题的计算分析,深入探索高超声速条件下振动能激发对飞行器气动力/热特性的影响.
[1]Votta R,Schettino A,Bon fi glioli A 2013Aerosp.Sci.Technol.25 253
[2]Shevyrin A A,Vashchenkov P V,Bondar Y A,Ivanov M S 2014Proceedings of the 29th International Symposium on Rare fi ed Gas DynamicsXi’an,China,July 13–18,2014 p155
[3]Bird G A 1994Molecular Gas Dynamics and The Direct Simulation of Gas Flows(Oxford:Oxford University Press)pp50–54
[4]Shen Q 2003Rare fi ed Gas Dynamics(Beijing:National Defense Industry Press)pp38,83–88(in Chinese)[沈青 2003稀薄气体动力学 (北京:国防工业出版社)第38,83—88页]
[5]Struchtrup H 2005Macroscopic Transport Equations for Rare fi ed Gas Flows(Berlin:Springer)p27
[6]Chapman S,Cowling T G 1970The Mathematical Theory of Non-uniform Gases(Cambridge:Cambridge University Press)pp46–48
[7]Cercignani C 1988The Boltzmann Equation and Its Applications(New York:Springer Science Business Media)pp64–66
[8]Kremer G M 2010An Introduction to the Boltzmann Equation and Transport Processes in Gases(Berlin:Springer)p37
[9]Bhatnagar P L,Gross E P,Krook M 1954Phys.Rev.94 511
[10]Holway L H 1966Phys.Fluids9 1658
[11]Shakhov E M 1968Fluid Dynam.3 95
[12]Yang J Y,Huang J C 1995J.Comput.Phys.120 232
[13]Li Z H,Zhang H X 2002Acta Mech.Sin.34 145(in Chinese)[李志辉,张涵信 2002力学学报 34 145]
[14]Olga I R,Alexey P P,Irina A G 2013Comput.Fluids80 71
[15]Titarev V,Dumbser M,Utyuzhnikov S 2014J.Comput.Phys.256 17
[16]Li Z H,Peng A P,Fang F,Li S X,Zhang S Y 2015Acta Phys.Sin.64 224703(in Chinese)[李志辉,彭傲平,方方,李四新,张顺玉2015物理学报64 224703]
[17]Xu K,Huang J C 2010J.Comput.Phys.229 7747
[18]Cai Z N,Li R 2014J.Comput.Phys.267 63
[19]Li Z H,Peng A P,Zhang H X,Yang J Y 2015Prog.Aerosp.Sci.74 81
[20]Li Z H 2001Ph.D.Dissertation(Mianyang:China Aerodynamics Research and Development Center)(in Chinese)[李志辉 2001博士学位论文 (绵阳:中国空气动力研究与发展中心)]
[21]Li Z H,Zhang H X 2004J.Comput.Phys.193 708
[22]Li Z H,Zhang H X 2005Adv.Mech.Sin.35 559(in Chinese)[李志辉,张涵信 2005力学进展 35 559]
[23]Li Z H,Zhang H X 2007Acta Mech.Sin.:PRC23 121
[24]Li Z H,Zhang H X 2009J.Comput.Phys.228 1116
[25]Li Z H,Peng A P,Zhang H X,Deng X G 2011Sci.Sin.:Phys.Mech.Astron.54 1687
[26]Peng A P,Li Z H,Wu J L,Jiang X Y 2016Chin.J.Theor.Appl.Mech.48 95(in Chinese)[彭傲平,李志辉,吴俊林,蒋新宇2016力学学报48 95]
[27]Peng A P,Li Z H,Wu J L,Jiang X Y 2016J.Comput.Phys.327 919
[28]Li Z H,Wu J L,Jiang X Y,Ma Q 2015Acta Aeronaut.Astron.Sin.36 201(in Chinese)[李志辉,吴俊林,蒋新宇,马强2015航空学报36 201]
[29]Li H Y 2007Ph.D.Dissertation(Mianyang:China Aerodynamics Research and Development Center)(in Chinese)[李海燕 2007博士学位论文 (绵阳:中国空气动力研究与发展中心)]
[30]Li H Y,Li Z H,Luo W Q,Li M 2014Sci.Sin.:Phys.Mech.Astron.44 194(in Chinese)[李海燕,李志辉,罗万清,李明2014中国科学:物理学力学天文学44 194]
[31]Boyd I D,Josyula E 2011Phys.Fluids23 057101
[32]Yang H S 2013M.S.Thesis(Shanghai:Shanghai Jiaotong University)(in Chinese)[杨浩森2013硕士学位论文(上海:上海交通大学)]
[33]Li Z,Zhu T,Levin D A 2013AIAA Paper AIAA2013-1201
[34]Wang C S,Uhlenbeck G E,Boer J D 1964Studies in Statistical Mechanics(Amsterdam:North-Holland Publishing Company)p2
[35]Wang C S(translated by Ying C T,Zhang C Z)1994The Kinetic Theory of a Gas(Beijing:Atom Energy Press)pp71–75(in Chinese)[王承书著 (应纯同,张存镇译)1994气体分子运动论 (北京:原子出版社)第71—75页]
[36]Morse T F 1964Phys.Fluids7 2012
[37]Andries P,Le Tallec P,Perlat J P,Perthame B 2000Eur.J.Mech.B:Fluid19 813
[38]Brull S,Schneider J 2009Continuum Mech.Thermodyn.20 489
[39]Rykov V A 1975Fluid Dynam.+10 959
[40]Rykov V A,Titarev V A,Shakhov E M 2008Fluid Dynam.+43 316
[41]Rykov V A,Titarev V A,Shakhov E M 2007Comp.Math.Math.Phys.+47 136
[42]Wu L,White C,Thomas J S,Reese J M,Zhang Y H 2015J.Fluid Mech.763 24
[43]Tantos C,Valougeorgis D,Frezzotti A 2015Int.J.Heat Mass Trans.88 636
[44]Tantos C,Ghiroldi G P,Valougeorgis D,Frezzotti A 2016Int.J.Heat Mass Trans.102 162
[45]Allu P,Mazumder S 2016Int.J.Heat Mass Tran.100 165
[46]Li Z H,Jiang X Y,Wu J L,Peng A P 2014Chin.J.Theor.Appl.Mech.46 336(in Chinese)[李志辉,蒋新宇,吴俊林,彭傲平2014力学学报46 336]
[47]Wu J L,Peng A P,Li Z H,Fang M 2015Acta Aerodynam.Sin.33 5(in Chinese)[吴俊林,彭傲平,李志辉,方明2015空气动力学学报33 5]
[48]Jiang X Y,Li Z H,Wu J L 2014Chin.J.Comput.Phys.31 403(in Chinese)[蒋新宇,李志辉,吴俊林2014计算物理31 403]
[49]Xu A G,Zhang G C,Li Y J,Li H 2014Prog.Phys.Sin.34 136(in Chinese)[许爱国,张广财,李英骏,李华 2014物理学进展34 136]
[50]Ying C T 1990Theory and Application of Gases Transport(Beijing:Tsinghua University Press)p62(in Chinese)[应纯同 1990气体输运理论及应用 (北京:清华大学出版社)第62页]
[51]Laurent B,Bérénice G,Milana P C,Francesco S 2013Proc.Appl.Math.Mech.13 353
[52]Bird G A 2005Proceedings of the 24th International Symposium on Rare fi ed Gas DynamicsMelville,Canada 2005 p541
Validation and analysis of gas-kinetic uni fi ed algorithm for solving Boltzmann model equation with vibrational energy excitation∗
Peng Ao-Ping1)Li Zhi-Hui1)2)3)†Wu Jun-Lin1)Jiang Xin-Yu1)
1)(Hypervelocity Aerodynamics Institute,China Aerodynamics Research and Development Center,Mianyang 621000,China)
2)(State Key Laboratory of Aerodynamics,China Aerodynamics Research and Development Center,Mianyang 621000,China)
3)(National Laboratory for Computational Fluid Dynamics,Beijing 100191,China)
2 May 2017;revised manuscript
19 May 2017)
With the increase of temperature in fl ow fi eld,gas molecules possess not only rotational degree of freedom,but also vibrational energy excitation.In order to simulate and study the in fl uence of internal energy excitation on polyatomic gas fl ow with high temperature and high Mach number,according to the general Boltzmann equation,we consider the rotational and vibrational energy modes as the independent variables of gas molecular velocity distribution function.It is assumed that the rotational and vibrational energy modes are described by continuous distribution with degree of freedom and temperature.Based on the Borgnakke-Larsen collision model used in direct simulation Monte Carlo(DSMC)method,the collision term of Boltzmann equation with internal energy excitation is divided into elastic and inelastic collision terms.The inelastic collision is decomposed into translational-rotational energy relaxation and translational-rotationalvibrational energy relaxation according to a certain relaxation rate obtained from the reciprocalities of rotational and vibrational collisions numbers per one elastic collision.Then a kind of Boltzmann model equation considering the excitation of vibrational energy is constructed.For showing the consistency between the present model equation and Boltzmann equation,the conservation of summational invariants and the H-theorem of this model are proved.When solving the present model equation with numerical methods,because of the continuous energy modes,it is difficult to simulate this model equation directly.In this paper,three control equations are derived and solved by the LU-SGS(lower-upper symmetric Gauss-Seidel)method,and the cell-centered fi nite volume method with multi-block patched grid technique in physical space.As a result,these gas-kinetic uni fi ed algorithm(GKUA)with vibrational energy excitation has been developed.Results are presented for N2with different Knudsen numbers around cylinder from continuum to rare fi ed gas fl ow by using the present Boltzmann model equation,GKUA with simple gas model,and DSMC method.Very good agreement between the present model and DSMC results is obtained,which shows that the accuracy and reliability of the present model.Comparing the translational,rotational,vibrational,and total temperatures computed by different methods,the e ff ects of the rotational and vibrational degrees of freedom are demonstrated.For the simple gas model,the translational temperature is much higher than those for the other two models with internal energy excitation.At the same time,the distance from shock wave to wall for the simple gas model is about twice those for the other two models.On the other hand,the obtained aerodynamic force coefficients of the cylinder are increasing according to the sequence from the simple gas model to the rotational energy excitation model to the vibrational energy excitation model,but the variation range is very small.By reducing the gas characteristic vibrational temperature,the temperature after the shock wave is much lower,and the heat fl ux declines evidently at the stagnation point with the same temperature as the wall temperature.This implies that with the wall temperature increasing the heat fl ux declines.
Boltzmann equation,vibrational energy excitation,gas-kinetic uni fi ed algorithm,thermodynamics non-equilibrium e ff ect
(2017年5月2日收到;2017年5月19日收到修改稿)
10.7498/aps.66.204703
∗国家重点基础研究发展计划(批准号:2014CB744100)和国家自然科学基金(批准号:11325212,91016027)资助的课题.
†通信作者.E-mail:zhli0097@x263.net
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
PACS:47.45.Ab,47.45.–n,47.85.Gj,34.50.EzDOI:10.7498/aps.66.204703
*Project supported by the National Basic Research Program of China(Grant No.2014CB744100)and the National Natural Science Foundation of China(Grant Nos.11325212,91016027).
†Corresponding author.E-mail:zhli0097@x263.net

