欠匹配型磁绝缘感应电压叠加器次级阻抗优化方法∗

魏浩 孙凤举 呼义翔 邱爱慈

1)(西安交通大学,电力设备电气绝缘国家重点实验室,西安 710049)

2)(西北核技术研究所,强脉冲辐射环境模拟与效应国家重点实验室,西安 710024)

欠匹配型磁绝缘感应电压叠加器次级阻抗优化方法∗

魏浩1)2)†孙凤举2)呼义翔2)邱爱慈1)2)

1)(西安交通大学,电力设备电气绝缘国家重点实验室,西安 710049)

2)(西北核技术研究所,强脉冲辐射环境模拟与效应国家重点实验室,西安 710024)

磁绝缘感应电压叠加器,次级阻抗,磁绝缘最小电流,鞘层电子流再俘获

磁绝缘感应电压叠加器(MIVA)次级阻抗对脉冲功率驱动源和负载之间的功率耦合具有重要影响.基于稳态磁绝缘Creedon层流理论和鞘层电子流再俘获(re-trapping)理论,建立了负载欠匹配型MIVA电路分析方法,数值分析获得了MIVA输出参数(输出电压、阴/阳极电流和电功率)随负载欠匹配程度的变化规律.考虑阴极传导电流作为闪光X射线照相二极管的有效电流,建立了以MIVA末端X射线剂量率最大为目标的次级阻抗优化方法.获得了欠匹配型MIVA次级优化阻抗Z∗op的变化规律:随着X射线剂量率对电压依赖程度提高,欠匹配型MIVA次级优化阻抗Z∗op呈指数降低;负载阻抗越大,Z∗op越大.

1 引 言

磁绝缘感应电压叠加器(magneticallyinsulated induction voltage adder,MIVA)可产生电压数十兆伏、电流数百千安的高功率电脉冲[1−5].MIVA作为强流脉冲功率加速器的驱动源,在闪光X射线照相、强脉冲辐射环境模拟等领域具有重要应用[3−9].MIVA通常由多级兆伏级感应腔串联组成,次级采用磁绝缘传输线(magneticallyinsulated transmission line,MITL)[10,11]实现电功率叠加和传输.MIVA次级MITL阻抗(包括阻抗大小和变换形式)对MIVA输出参数以及驱动源和负载之间的功率耦合具有重要影响[12,13].

对于十数级感应腔串联MIVA装置,在次级电脉冲到达负载前,脉冲前沿损失部分电子在阳极上,为后续脉冲建立磁绝缘提供所需磁场,次级MITL运行在磁绝缘最小电流或自限制流工作点[14−16].当电脉冲传输至负载时,若负载阻抗大于或等于MITL运行阻抗,磁绝缘特性完全由传输线本身确定,与负载无关,该类型MIVA为负载匹配型.若负载阻抗小于MITL运行阻抗,反射波由负载向MIVA传输,MIVA末端电压降低,阴、阳极电流增大,该类型MIVA为负载欠匹配型[16−18].

MIVA次级电流由阴极传导电流和鞘层电子流两部分组成.对于一些高功率负载(例如用于产生高能脉冲X射线的闪光照相二极管),只有阴极传导电流才能作为负载有效电流,鞘层电子流对负载X射线剂量率无贡献[1,3,19].对于负载匹配型MIVA,随着MIVA输出电压提高,阴极电流占总电流比例Ic/Ia降低.当MIVA输出电压大于10 MV时,Ic/Ia小于40%[1,12],大部分电流以鞘层电子流形式存在,这极大地降低了MIVA装置的电流和功率利用效率.近年来国际上提出MIVA末端采用低阻抗照相二极管(相对于150—350 Ω的傍轴和浸磁等高阻抗二极管,自磁箍缩或负极性杆箍缩二极管的阻抗较低,一般约30—50 Ω),使MIVA工作在负载欠匹配模式,通过鞘层电子流再俘获,来减小鞘层电子流,增大阴极传导电流[20−24].

文献[25]给出了负载匹配型MIVA次级阻抗优化方法.由于欠匹配型MIVA输出参数同时受次级阻抗和负载阻抗影响,其电路分析方法和次级阻抗优化方法与负载匹配型MIVA不同.本文基于磁绝缘Creedon层流理论和鞘层电子流再俘获理论,建立了欠匹配型MIVA电路分析方法;以闪光照相二极管X射线剂量率最大为优化目标,考虑阴极传导电流作为负载有效电流,建立了欠匹配型MIVA次级阻抗优化方法.需要指出的是,本文中次级阻抗优化主要针对MIVA输出端(最末级感应腔对应次级MITL)次级阻抗数值,假定MIVA各级感应腔对应次级MITL运行阻抗线性增大.

2 负载欠匹配型MIVA电路分析方法

2.1 磁绝缘鞘层电子流再俘获理论

图1给出了磁绝缘鞘层电子流再俘获示意图.在磁绝缘前行波到达负载前,前行波经过区域运行在磁绝缘最小电流工作点(U0,I0),前行波传输特征阻抗为MITL运行阻抗Zop.当前行波抵达负载时,由于负载欠匹配,反射波由负载向MIVA反向传输,反射波经过区域MITL线电压由U0降低至Ud,阳极电流由最小电流I0增大为Id,鞘层电子流中部分空间电子被重新俘获至阴极,阴极传导电流Ic增加,鞘层电子流If减小,鞘层变薄(图1中反射波经过区域电子鞘层紧贴阴极表面),反射波传输特征阻抗接近MITL真空阻抗Zv[13,21].反射波传输速度vref取决于负载Zd和次级运行阻抗Zop之间阻抗失配程度,两者不匹配程度越高,vref越大,vref通常约为0.3—0.6倍光速[13].

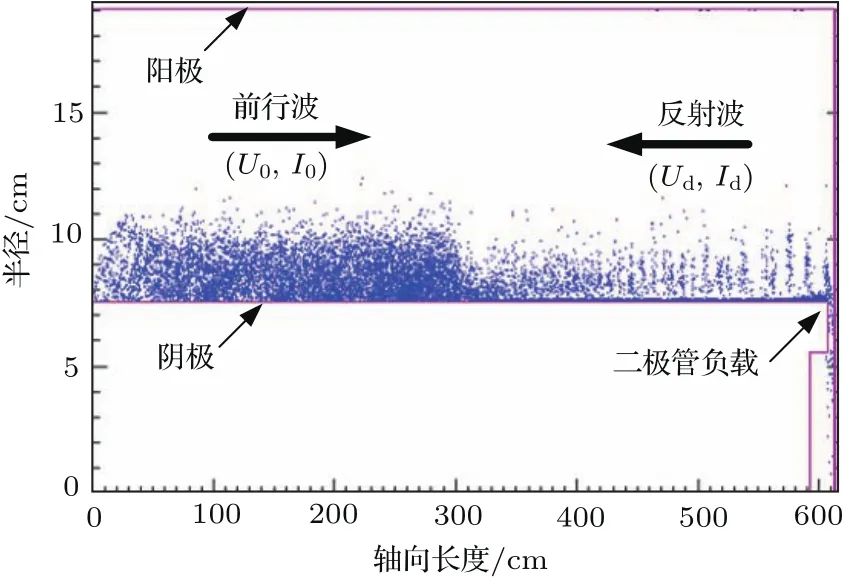
图1 (网刊彩色)磁绝缘鞘层电子流再俘获示意图[4]Fig.1. (color online)Sketch of re-trapping the magnetically-insulated sheath electron fl ow[].

2.2 负载欠匹配型MIVA电路分析方法

图2给出了负载欠匹配型MIVA工作曲线.图中实线为前行波工作曲线,负载匹配型MIVA(Zd≥Zop)磁绝缘运行在该曲线上.虚线是由负载Zd确定的工作曲线,与负载大小密切相关(如图2中A,B,C).当MIVA由前行波工作点O(U0,I0)调整至负载限定工作点A(Ud,Id)时,需经过反射波工作曲线(图2中虚线),曲线斜率为MITL真空阻抗Zv.反射波和负载限定工作曲线的电路方程分别为

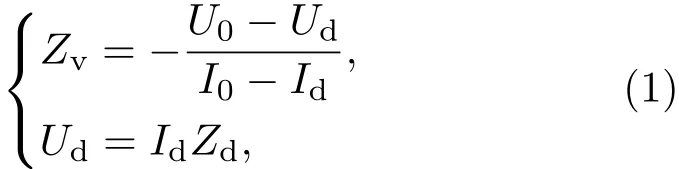
其中,磁绝缘前行波的线电压U0和阳极电流I0为

其中,Vs,Zs分别为MIVA前级脉冲源的等效馈入电压和等效驱动阻抗,可由负载匹配型MIVA电路分析获得[25,26].

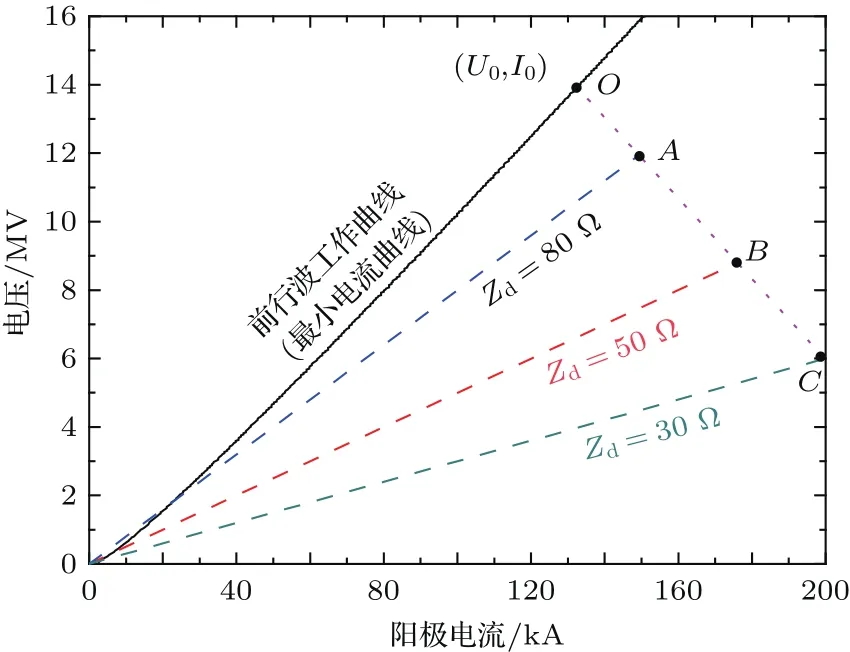
图2 磁绝缘鞘层电子流再俘获时MIVA运行曲线Fig.2.Operating cures of MIVA when the sheath electron fl ow is re-trapped.

联合(1)和(2)式推导得到鞘层电子流俘获后MITL电压Ud和阳极电流Id分别为

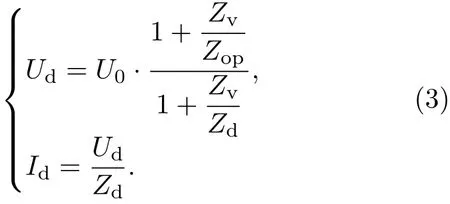
(3)式表明欠匹配型MIVA输出电压Ud取决于次级阻抗Zop和负载阻抗Zd.

由稳态磁绝缘Creedon层流理论[18,27],MIVA输出端阴极传导电流Ic为

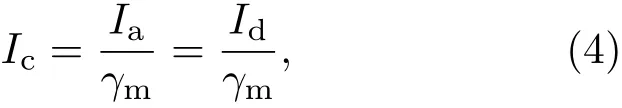
其中,γm为磁绝缘电子鞘层边界的相对论因子,γm为磁绝缘线电压Ud、阳极电流Id和MITL几何阻抗因子g的隐性函数[18,27],

其中,Iav为阿尔芬电流常数,Iav≈8500 A[18,27].阳极相对论因子γ00和几何因子g分别为[18,27]

由(3)—(6)式推导得到,阴极电流Ic可表征为次级阻抗Zop和负载阻抗Zd的隐性函数,

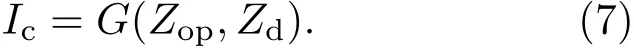
虽然无法给出(7)式的解析表达式,但可以通过数值方法求解.

2.3 MIVA输出参数随负载欠匹配程度的变化规律

假定10级感应腔串联MIVA输出端磁绝缘最小电流工作点为:U0=14 MV,I0=133 kA,Zop=105 Ω.MIVA输出参数(输出电压、阴/阳极电流和电功率)随负载阻抗的变化规律如图3所示.随着负载阻抗Zd减小,MIVA输出电压逐渐降低,阴/阳极电流均逐渐增大,阴极电流占阳极电流比例Ic/Ia增大.与磁绝缘最小电流工作点相比,当负载阻抗Zd为80 Ω时,负载电压Ud降低至12 MV,阴、阳电流分别为150和113 kA;当Zd减小至40 Ω时,Ud=7.5 MV,Ia=186 kA,Ic=176 kA,鞘层电子流仅10 kA.随着负载阻抗Zd减小,MIVA向负载耦合的总电功率降低,但有效电功率先增大、后减小.当Zd=61 Ω时,MIVA向负载耦合的有效电功率最大.

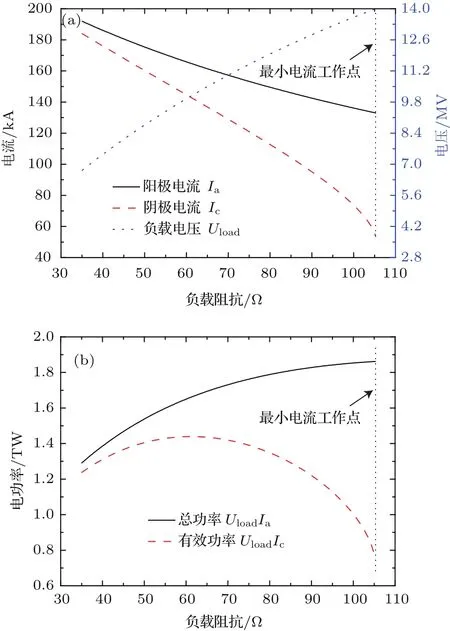
图3 10级MIVA装置输出参数随负载欠匹配程度的变化规律 (a)负载电压和阴、阳极电流随负载阻抗的变化;(b)总电功率、有效电功率随负载阻抗的变化Fig.3.Change law of the output parameters depending on the under-matching degree of loads:(a)Load voltage,anode current,and cathode current varies with the load impedances;(b)total and e ff ective electrical power functions as the load impedances.

3 负载欠匹配型MIVA次级阻抗优化

3.1 以负载辐射X射线剂量率最大为目标的次级阻抗优化方法

以驱动闪光照相二极管的MIVA装置为例,通过优化MIVA次级MITL运行阻抗Zop,使MIVA末端二极管辐射X射线剂量率最大.已有研究表明,高能脉冲闪光照相二极管X射线剂量率与二极管电压Ud、阴极传导电流Ic的定标关系为[3,25]

其中,α,β均为常数,其取值与二极管特性(二极管类型、工作状态等)密切有关[3].现有研究表明,常数α取值范围为1＜α＜3[3].当α=β=1时,(8)式为MIVA耦合到二极管负载上的有效电功率.由于β仅影响剂量率绝对值,本文假定β≡1.

将(3)和(7)式的二极管电压、电流公式代入(8)式,得到二极管剂量率为

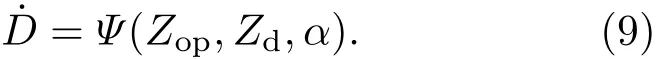
虽然无法给出(9)式的显性表达式,(9)式表明X射线剂量率取决于MITL运行阻抗Zop、负载阻抗Zd和定标系数α.以X射线剂量率最大为目标函数的MIVA次级阻抗优化问题可表示为:

(11)式中优化变量Zop下限值是为了满足负载欠匹配条件,上限值Zop_upper通常出于MIVA工程实际考虑.由(2)式可知,当给定前级脉冲源馈入参数Zs和Vs时,线电压U0随Zop增大而线性增加,但受感应腔最高耐受电压的限制,U0存在最大值,即次级阻抗存在最大值Zop_upper.

3.2 运行阻抗对MIVA输出参数的影响规律

给定MIVA前级馈入脉冲源参数Vs=22 MV,Zs=60 Ω(MIVA感应腔串联级数n=10,每级并联馈入脉冲路数m=1,每路电脉冲幅值电压1.1 MV,驱动阻抗6 Ω).假定每级感应腔最高耐受电压为1.5 MV,由(2)式计算运行阻抗上限值Zop_upper=129 Ω.

由于二极管的实际工作阻抗随时间动态变化,只能近似给出稳态阶段阻抗变化范围.现有研究表明,对于低阻抗闪光照相二极管(自磁箍缩或负极性杆箍缩二极管),其阻抗变化范围为30—50 Ω[22],本文选取三个典型负载阻抗值(30,40,50 Ω)作为优化对象.

图4—图6分别给出了不同负载Zd时,MIVA输出电压Ud、阴阳极电流比例Ic/Ia和电功率随运行阻抗Zop的变化规律.对于给定负载阻抗Zd,随着运行阻抗Zop降低(但仍满足欠匹配条件Zop＞Zd),由于MIVA次级MITL与负载之间的阻抗失配程度减弱,MIVA输出电压Ud逐渐增大.当Zop=Zd(MIVA与负载阻抗匹配)时,负载电压Ud取最大值,Zd为30,40,50 Ω时,Ud最大值分别为7.3,8.8和10 MV.若Zop继续降低,当Zop＜Zd时,MITL运行在磁绝缘最小电流工作点,MIVA输出特性与负载大小无关,负载电压Ud随Zop减小逐渐降低.

图4 运行阻抗对MIVA负载电压的影响Fig.4.The load voltage functions as the operating impedances.

由图5可知,对于给定负载Zd,随着Zop降低(阻抗失配程度减弱),鞘层电子流再俘获作用减弱,阴、阳极电流比例Ic/Ia减小;当Zop≤Zd时,无鞘层电子流再俘获,随着Zop降低,MITL线电压减小,Ia,Ic和Ic/Ia均增大.

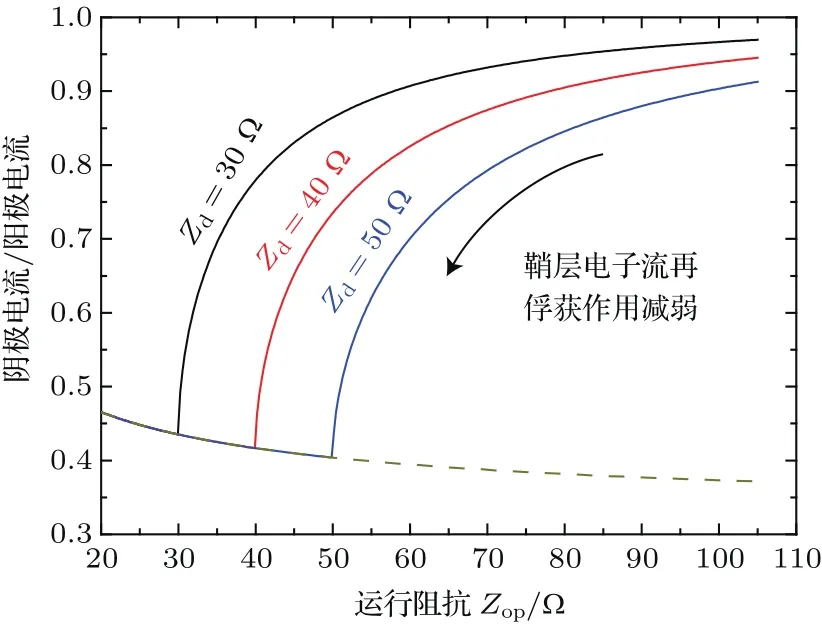
图5 运行阻抗对阴、阳极电流比例Ic/Ia的影响Fig.5.The ratio of the cathode current and anode current varies with the operating impedances.

由图6可知,随着运行阻抗Zop降低,MIVA输出总电功率P和有效电功率Peff均先增大后减小,但峰值P和峰值Peff对应的运行阻抗不同.当Zop=Zd(MIVA次级MITL与负载匹配)时,总电功率P最大,但此时有效电功率Peff极低,Peff在Zop＞Zd(负载欠匹配)时获得.

图6 (网刊彩色)运行阻抗对MIVA输出电功率的影响Fig.6.(color online)Electrical power of MIVA varies with the operating impedances.

3.3 使二极管辐射X射线剂量率最大的次级优化阻抗

图7 给出了MIVA末端X射线二极管选取三个典型阻抗值(Zd分别为30,40,50 Ω)时,最大X射线剂量率随次级优化阻抗p和定标系数α的变化规律.需要指出的是,图7所示为剂量率的相对值(假定(8)式中β=1).图8给出了使剂量率最大的优化阻抗p(最佳阻抗)与定标系数α的关系.对于给定负载阻抗Zd,最佳阻抗p随α增大(剂量率对电压依赖程度提高)近似指数衰减,这与负载匹配型MIVA存在显著区别,后者最佳阻抗p随定标系数α增大而线性增加[26].两种类型MIVA次级优化阻抗变化规律不同的本质原因在于,MIVA输出电压随次级阻抗Zop的变化趋势不同,负载匹配型MIVA输出电压随Zop增加而增大,但欠匹配型MIVA输出电压随Zop增加反而逐渐减小(见图4).由(8)式可知,MIVA输出电压对X射线剂量率的影响程度很大(特别是定标系数α较大时).正是由于次级阻抗对两种类型MIVA输出电压影响规律的差异,导致最大剂量率对应的次级阻抗(最佳阻抗)随定标系数α的变化趋势不同.

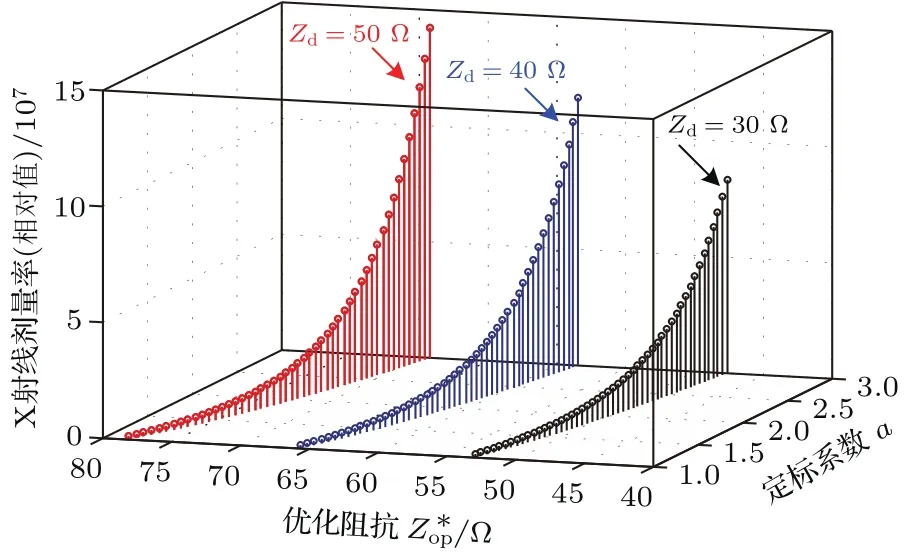
图7 三种典型负载阻抗下,二极管辐射X射线剂量率随定标系数α和优化阻抗Zo∗p的变化规律Fig.7. The radiated X-ray dose rate varies with the scaling factor α,and the optimized operating impedance Zo∗punder three typical load impedances.

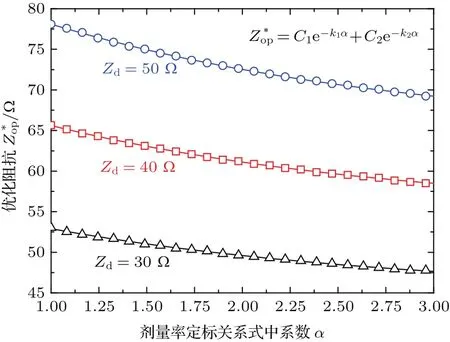
图8 三种典型负载阻抗时最佳阻抗Z∗op随定标系数α的变化规律Fig.8.Optimized operating impedance Z∗opvaries with the scaling factor α under three typical load impedances.

对于欠匹配MIVA,经数值拟合得到,使X射线剂量率最大的次级阻抗p与定标系数α的关系可表示为[26]

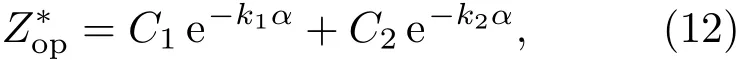
式中C1,C2和k1,k2为常数,取值与负载Zd、前级脉冲源等效驱动阻抗Zs相关[26].

4 结 论

基于稳态磁绝缘Creedon层流理论和鞘层电子流再俘获(re-tapping)理论,建立了负载欠匹配型MIVA电路分析方法和次级MITL运行阻抗优化方法.当给定次级运行阻抗时,获得了MIVA输出参数(输出电压、阴/阳极电流和电功率)随负载欠匹配程度的变化规律.当给定负载阻抗时,数值分析获得了次级运行阻抗对MIVA输出参数的影响规律.获得了使MIVA末端辐射X射线剂量率最大的次级优化阻抗值的变化规律:随着二极管X射线剂量率对电压依赖程度提高(定标系数α增大),最佳阻抗近似指数下降.本文建立的欠匹配MIVA电路分析方法和次级阻抗优化方法已应用于MIVA装置电路分析和物理设计.

[1]Smith I D 2004Phys.Rev.Spec.Top.Accel.Beams7 064801

[2]Smith I D,Bailey V L,Fockler J,Gustwiller J S,Johnson D L,Maenchen J E,Droemer D W 2000IEEE Trans.on Plasma Sci.28 1653

[3]Oliver B V 2008Proceeding of 17th IEEE High Power Particle Beams ConferenceXi’an,Shaanxi,China,July 7–11,2008 p1

[4]Thomas K 2014IEEE Pulsed Power SymposiumLoughborough,UK,March 18–20,2014,pp1–29

[5]Thomas K,Beech P,Brown S,Buck J,Burscough J,Clough S,Crotch I,Du ffY J,Goes C,Huckle I,Jones A,King A,Stringer B,Threadgold J,Trenaman S,Wheeldon R,Woodroofe M,Carboni V,DaSilva T,Galver B,Glazebrook W,Hanzel K,Pearce J,Pham J,Pomeroy S,Saunders W,Speits D,Warren T,Whitney B,Wilson J 2011Proceeding of 18th IEEE Pulsed Power ConferenceChicago,IL,June 19–23,2011 p1042

[6]Guo F,Zou W K,Gong B Y,Jiang J H,Chen L,Wang M,Xie W P 2017Phys.Rev.Accel.Beams20 020401

[7]Wei H,Sun F J,Qiu A C,Zeng J T,Liang T X,Yin J H,Hu Y X 2014IEEE Trans.Plasma Sci.42 3057

[8]Sun F J,Qiu A C,Yang H L,Zeng J T,Gai T Y,Liang T X,Yin J H,Sun J F,Cong P T,Huang J J,Su Z F,Gao Y,Liu Z G,Jiang X F,Li J Y,Zhang Z,Song G Z,Pei M J,Niu S L 2010High Power and Laser and Particle Beams22 936(in Chinese)[孙凤举,邱爱慈,杨海亮,曾江涛,盖同阳,梁天学,尹佳辉,孙剑锋,丛培天,黄建军,苏兆锋,高屹,刘志刚,姜晓锋,李静雅,张众,宋顾周,裴明敬,牛胜利2010强激光与粒子束22 936]

[9]Zhang T K,Han D,Wu Y C,Yan Y H,Zhao Z Q,Gu Y Q 2016Acta Phys.Sin.65 045203(in Chinese)[张天奎,韩丹,吴玉迟,闫永宏,赵宗清,谷渝秋 2016物理学报65 045203]

[10]Wei H,Sun F J,Hu Y X,Liang T X,Cong P T,Qiu A C 2017Acta Phys.Sin.66 038402(in Chinese)[魏浩,孙凤举,呼义翔,梁天学,丛培天,邱爱慈2017物理学报66 038402]

[11]Zhou J,Zhang P F,Yang H L,Sun J,Sun J F,Su Z F,Liu W D 2012Acta Phys.Sin.61 245203(in Chinese)[周军,张鹏飞,杨海亮,孙江,孙剑峰,苏兆锋,刘万东 2012物理学报61 245203]

[12]Bailey V,Corcoran P,Carboni V,Smith I,Johnson D L,Oliver B,Thomas K,Swierkosz M 2005Proceeding of 15th IEEE Pulsed Power ConferenceMonterey,CA,USA,June 13–15,2005 p322

[13]Bailey V L,Johnson D L,Corcoran P,Smith I,Maenchen J E,Molina I,Hahn K,Rovang D,Portillo S,Oliver B V,Rose D,Welsh D,Droemer D,Guy T 2003Proceeding of 14th IEEE International Pulsed Power ConferenceDallas,Texas,USA,June 15–18,2003 p399

[14]Ottinger P,Schumer J,Hinshelwood D,Allen R J 2008IEEE Trans.Plasma Sci.36 2708

[15]Ottinger P,Schumer J 2006Phys.Plasma13 063109

[16]Pate R C,Patterson J C,Dowdican M C,Ramirez J J,Hasti D E,Tolk K M,Poukey J W,Schneider L X,Rosenthal S E,Sanford T W,Alexander J A,Heath C E 1987Proceeding of 6th IEEE Pulsed Power ConferenceArlington,Virginia,1987 pp478–481

[17]Guo F,Zou W K,Chen L 2014High Power and Laser and Particle Beams26 045010(in Chinese)[郭帆,邹文康,陈林2014强激光与粒子束26 045010]

[18]Liu X S 2005High Pulsed Power Technologh(Beijing:National Defense Industry Press)pp128–262(in Chinese)[刘锡三 2005高功率脉冲技(北京:国防工业出版社)第128—262页].

[19]Zou W K,Deng J J,Song S Y 2007High Power and Laser and Particle Beams19 992(in Chinese)[邹文康,邓建军,宋盛义2007强激光与粒子束19 992]

[20]Bailey V L,Corcoran P,Johnson D L,Smith I,Oliver B,Maenchen J 2007Proceeding of 16th IEEE Pulsed Power ConferenceAlbuquerque,New Mexico,USA,June 17–22,2007 p1268

[21]Bailey V L,Corcoran P,Johnson D L,Smith I D,Maenchen J E,Rahn K D,Molina I,Rovang D C,Portillo S,Puetz E A,Oliver B V,Rose D V,Welch D R,Droemer D W,Guy T 2004Proceeding of 14th IEEE high Power Beams ConferenceDallas,Texas,USA,2004 p247

[22]Hahn K,B V Oliver,Cordova S R,Leckbee J,Molina I,Johnston M,Webb T,Bruner N,Welch D R,Portillo S,ZiskaD,Crotch I,Threadgold J 2009Proceeding of 17th IEEE Pulsed Power ConferenceWashington,DC,USA,June 28–July 2,2009 p34

[23]Hahn K,Maenchen J,Cordova S,Molina I,Portillo S,Rovang D,Rose D,Oliver B,Welch D,Bailey V,Johnson D L,Schamiloglu E 2003Proceeding of 14th IEEE Pulsed Power ConferenceDallas,Texas,USA,June 15–18,2003 p871

[24]Portillo S,Hahn K,Maenchen J,Molina I,Cordova S,Johnson D L,Rose D,Oliver B,Welch D 2003Proceeding of 14th IEEE Pulsed Power ConferenceDallas,Texas,USA,June 15–18,2003 p879

[25]Hu Y X,Sun F J,Zeng J T,Cong P T 2015Modern Appl.Phys.6 191(in Chinese)[呼义翔,孙凤举,曾江涛,丛培天2015现代应用物理6 191]

[26]Wei H 2017Ph.D.Dissertation(Xi’an:Xi’an Jiaotong University)(in Chinese)[魏浩 2017博士学位论文 (西安:西安交通大学)]

[27]Creedon J M 1975J.Appl.Phys.46 2946

Method of optimizing secondary impedances for magnetically-insulated induction voltage adders with impedance under-matched loads∗

Wei Hao1)2)†Sun Feng-Ju2)Hu Yi-Xiang2)Qiu Ai-Ci1)2)
1)(State Key Laboratory of Electrical Insulation and Power Equipment,Xi’an Jiaotong University,Xi’an 710049,China)
2)(State Key Laboratory of Intense Pulsed Radiation Simulation and E ff ect,Northwest Institute of Nuclear Technology,Xi’an 710024,China)

10 March 2017;revised manuscript

3 July 2017)

The magnetically-insulated induction voltage adder(MIVA)is a pulsed-power accelerator widely used in the X-ray fl ash radiography andγ-ray radiation simulation.The operating impedance of magnetically-insulated transmission line(MITL)on the secondary side of MIVA will produce signi fi cant in fl uence on the power coupling between the pulsedpower driving source and the terminal load.Therefore,optimizing the secondary impedance of MIVA to maximize the electrical-power or radiated output of load is critical for the design of MIVA facility.According to whether the MITL operating impedance is smaller than the load impedance,MIVAs can be divided into two different types,i.e.,the impedance-matched case and impedance undermatched case.For the impedance-matched MIVA,because the MITL of MIVA operates at the minimal current point or self-limited fl ow,the output of MIVA just depends on the MITL operating impedance and is independent of load.Correspondingly,the circuit analysis is relatively easy.However,for MIVA with impedance undermatched load,the analysis method is more complicated.Based on the classical Creedon theory of the magnetic insulation equilibrium and the sheath electron re-trapping theory,a circuit method is established for MIVA with impedance under-matched load.The analysis process consists of two steps.Firstly,the working point of the forward magnetic insulation wave is solved by the minimal current theory on the assumption that the MIVA is terminated by impedance-matched load.Then,the actual operating point after the re-trapping wave has passed is solved,in which the characteristic impedance of the re-trapping wave is treated as a vacuum impedance.And the relationship between the output parameters of MIVA,e.g.,the output voltage,the cathode and anode current,and the electrical power,and the undermatched extent of load is obtained numerically.Based on the analysis method,a method to optimize the secondary impedance of MIVA with ten-stage cavities stacked in series to drive X-ray radiographic diodes is developed.This optimization method aims at maximizing the radiated X-ray dose rate of the diode loads on the assumption that only the cathode current is available for the X-ray radiographic diode.The optimization secondary impedance,p,varying with the scaling factor,α,is achieved,whereαis the power exponent between the dose rate and the diode voltage().αis usually determined by the diode type,geometrical structure,and operating characteristics.It is found that the optimization secondary impedancepdecays exponentially with the increase of valueα,i.e.,the increase of the diode-voltage-dependent degree of the radiated X-ray dose rate.And the larger the load impedance,the larger the value ofpis.The circuit analysis method and the impedance optimization method developed in this paper are specially useful for the applications of MIVA in the fl ash radiographic fi elds.

magnetically-insulated induction voltage adders,secondary impedance,minimal current of magnetic insulation,re-trapping of sheath electron fl ow

(2017年3月10日收到;2017年7月3日收到修改稿)

10.7498/aps.66.208401

∗国家自然科学基金(批准号:11505138,51577156)资助的课题.

†通信作者.E-mail:weihao@nint.ac.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

PACS:84.70.+p,52.59.—f,02.60.Pn,84.30.NgDOI:10.7498/aps.66.208401

*Project supported by the National Natural Science Foundation of China(Grant Nos.11505138,51577156).

†Corresponding author.E-mail:weihao@nint.ac.cn