融合散斑干涉技术的阵列式洛伦兹力微颗粒探测方法∗
代尚军 吴思进 王晓东3) 史祎诗3)
1)(中国科学院大学材料科学与光电技术学院,北京 100049)
2)(北京信息科技大学仪器科学与光电工程学院,北京 100192)
3)(中国科学院光电研究院,北京 100094)
融合散斑干涉技术的阵列式洛伦兹力微颗粒探测方法∗
代尚军1)吴思进2)王晓东1)3)†史祎诗1)3)‡
1)(中国科学院大学材料科学与光电技术学院,北京 100049)
2)(北京信息科技大学仪器科学与光电工程学院,北京 100192)
3)(中国科学院光电研究院,北京 100094)
阵列式,洛伦兹力,散斑干涉,无损检测
提出了一种阵列式洛伦兹力微颗粒探测法,该方法结合了散斑干涉技术的全场位移测量、分辨率高等特性与洛伦兹力微颗粒探测法中探测量为矢量、可探测内部缺陷等优势,探索了一种实时、在线、原位的缺陷检测方法.针对阵列式洛伦兹力微颗粒探测法中阵列式排布的多个悬臂梁位移测量问题,设计了大剪切数字散斑干涉系统,使来自于被测悬臂梁和安装悬臂梁的横梁的反射光发生干涉,形成剪切干涉,通过对相位差进行分析获得悬臂梁的绝对位移,并且以洛伦兹力及悬臂梁末端的位移量为中间量建立了散斑干涉相位差与缺陷体积之间的关系.本文通过实验成功获得了悬臂梁全场位移量以及缺陷的体积,通过散斑干涉的方法测量悬臂梁位移量理论分辨率可达30 nm,这使洛伦兹力微颗粒探测法具备了微米级缺陷的探测能力.
1 引 言
随着工业技术的发展与工艺水平的提高,各种金属材料已经广泛应用在军工、建筑、工业生产等各行各业中.在金属材料的加工过程以及使用工程中,受多方面因素影响,诸如缩孔、夹渣、腐蚀、疲劳裂纹等缺陷都随之产生.这些缺陷会对材料的使用寿命、力学性能等产生直接影响,并且会逐渐发展形成裂纹,最终导致断裂,造成巨大损失[1].例如,高速列车在加速和制动过程中以及通过钢轨接缝、弯道和道岔时,长期对钢轨产生强烈摩擦、挤压、弯曲和冲击,使钢轨产生疲劳缺陷.缺陷一旦产生就易于快速扩展,造成钢轨折断直接影响行车的安全.而在各类缺陷中,特别是隐藏在材料和构件近表面的缺陷更具隐蔽性和危险性.可见对微颗粒或缺陷进行可靠、定期、有效的探测和监测具有重要的生产意义,可减少事故的发生、减少经济损失,还可提高加工效率、减少加工成本.因此开发有效简便、非接触、无损检测方法十分必要,且具有重要的、现实的国民经济和国防科技意义[2−5].
2012年本课题组提出一种基于电磁感应原理的新型缺陷检测方法——洛伦兹力微颗粒探测法,基于该方法成功探测到了300µm的缺陷.从测量原理部分可知,洛伦兹力微颗粒探测法的探测量电磁力为矢量,这一特性决定了相对于涡电流检测等传统方法该方法可以获知更丰富的缺陷信息,如缺陷的形状、裂纹的空间分布等[6,7].但该方法采用单个永磁体作为测量探头,单个永磁体的电磁敏感区域为1 mm量级,对于面积较大的待测试样需多次扫描才能获得试样中缺陷的统计信息.本文将电子散斑干涉方法引入洛伦兹力微颗粒探测法中,提出了一种阵列式洛伦兹力微颗粒探测法,有望实现快速准确地对导体中的缺陷进行探测及定位.
阵列式洛伦兹力微颗粒探测法中,需对阵列排布的多个悬臂梁在缺陷存在时产生的位移变化量同时进行监测.这种测量存在以下难点:首先阵列式排布的多个悬臂梁位移量需同时测量,目前尚无有效方法能对一排等距的多个永磁体位移量进行同时测量,而阵列式排布的永磁体-悬臂梁系统为多排多列,这又增加了测量难度;其次阵列排布的两排永磁体之间从光学测量角度还存在景深问题,无商业位移传感器能较好地解决该问题;更为重要的是,作用于悬臂梁上的反作用力分量及方向、扭矩等力学特征信息与缺陷的体积、裂纹的方向等相关,而上述力学特征作用到悬臂梁上,体现在整个悬臂梁各部分的离面位移量分布不同.数字散斑干涉技术属于全场测量,可获得整个悬臂梁的离面位移分布,进而通过分析可获得缺陷的特征信息[8−13].本文提出的阵列式洛伦兹力微颗粒探测法结合了数字散斑干涉全场、分辨率高等特性,以及洛伦兹力微颗粒中探测量为矢量、可探测内部缺陷等优势,探索了一种快速、高分辨率、实时、在线、原位的缺陷检测方法.
2 阵列式洛伦兹力微颗粒探测法
在洛伦兹力微颗粒探测法的基础上提出了如图1所示的阵列式探测法,整个测量系统包括:阵列式测量探头、旋转台、大剪切数字散斑干涉微变形测量系统、待测试样以及数据处理系统等.其中阵列探头排布方式如图1所示,两排永磁体相间排布,每排多个永磁体等距排布.
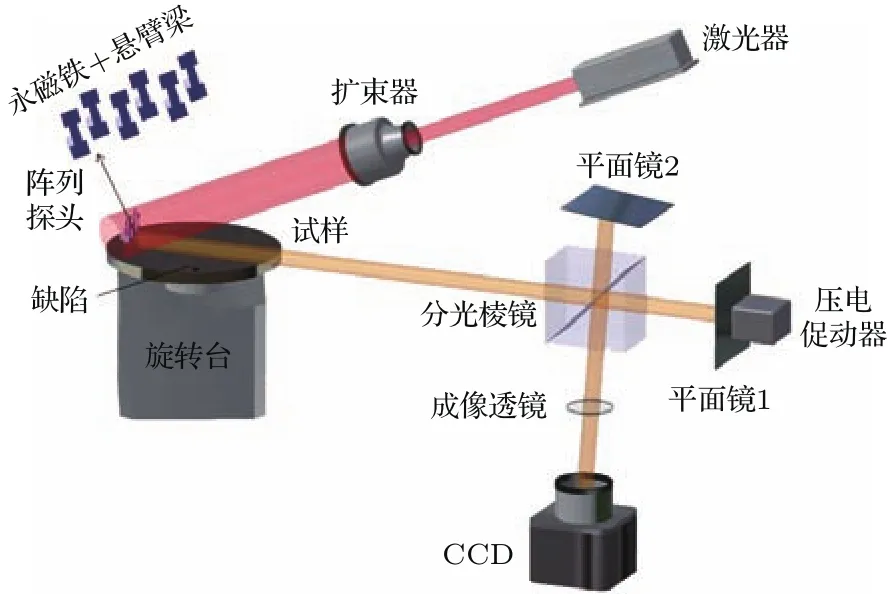
图1 阵列式洛伦兹力微颗粒探测法Fig.1.Principle of the Lorentz force particle analyzer with an array probe based on speckle pattern interferometry.
将数字散斑干涉技术引入到阵列式洛伦兹力微颗粒探测法中,用于测量由缺陷引起的悬臂梁位移量,整个测量过程如图2所示.
如图2所示,阵列式洛伦兹力微颗粒探测法测量过程可分为以下三个部分:缺陷的存在导致悬臂梁位移量发生变化;采用数字散斑干涉方法测量悬臂梁位移量;悬臂梁位移量转化为缺陷体积.
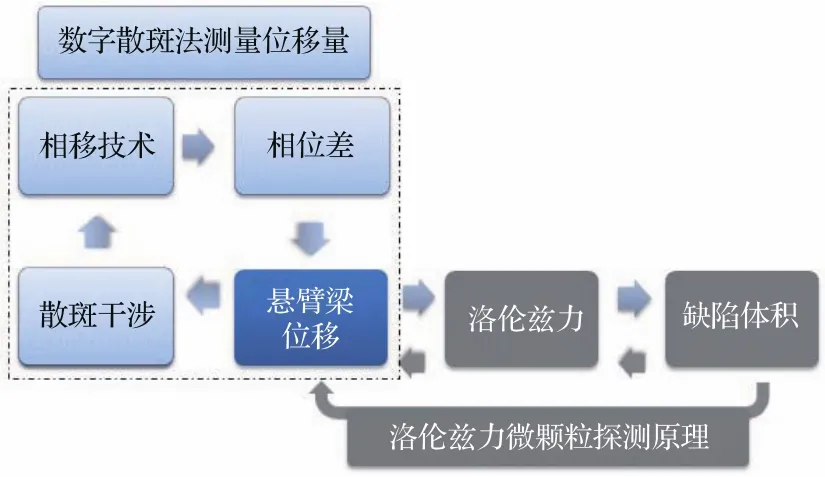
图2 基于数字散斑干涉技术的洛伦兹力微颗粒分析仪测量流程图Fig.2.Flow chart for detecting fl aws by Lorentz force particle analyzer based on speckle pattern interferometry.
2.1 阵列式洛伦兹力微颗粒探测法原理
洛伦兹力微颗粒探测原理如图3(a)所示.永磁体磁场渗透到待测试样中,本文将待测试样中的磁场作用区域称之为电磁敏感区,空间磁场可由(1)式近似获得:

其中m是磁矩,R为指向场点的位置矢量.
根据欧姆定律,与导体存在相对运动的永磁体在导体中感生出涡电流J,

式中ϕ是电势,V是相对速度,σ是试样电导率.
涡电流与永磁体相互作用产生洛伦兹力F作用于导体上,

根据牛顿第三定律,有一大小相等、方向相反的反作用力F0作用在永磁体上.如图3(b)所示:当导体中存在缺陷且经过电磁敏感区时,涡电流受到扰动或涡电流重新分布(变为J′)进而导致洛伦兹力随之发生变化().可见通过检测洛伦兹力的变化量分析可获得缺陷的存在与否及其特征信息.基于该原理,实验中成功探测到了300µm的缺陷[14−17].

图3 (网刊彩色)洛伦兹力微颗粒探测原理[] (a)无缺陷;(b)有缺陷Fig.3.(color online)Principle of the Lorentz force particle analyzer[]:(a)Without fl aw;(b)with fl aw.
洛伦兹力的变化量由黏接在永磁体上的悬臂梁探测获得,即永磁体受力后作用于悬臂梁使其发生形变.如图1中的阵列式洛伦兹力探测法中,缺陷经过某一永磁体电磁敏感区时,悬臂梁的位移量随之变化,而无缺陷经过的其他悬臂梁则无位移变化量.其中图1所示阵列式探头中,各永磁体磁敏感区域互不干扰,但从测量角度,磁敏感区域相互补充,无测量盲区.其中由洛伦兹力微颗粒探测法原理所述:体积不同的缺陷导致永磁体受到的作用力变化量不同,进而体现在悬臂梁的位移量有所区别.因此通过对悬臂梁位移量的精确测量分析可获得缺陷的体积,可见要探测缺陷的特征信息,关键在于对悬臂梁位移量的测量及分析.
2.2 数字散斑干涉方法测量悬臂梁位移量
针对上述阵列式排布悬臂梁测量问题,提出并开发了一种基于数字散斑干涉的动态微变形测量方法.测量过程如图2所示,在悬臂梁变形前后分别采集4幅散斑干涉图进行相移计算获得相位差,再经过滤波和解包裹等处理求得悬臂梁位移量[18].
数字散斑干涉动态微变形测量方法采用数字散斑干涉测量原理进行悬臂梁位移测量.数字散斑干涉技术是一种针对非光学表面物体(以漫反射现象为主)进行测量的光学干涉技术,能够测量物体的三维变形、应变、振动分布以及无损检测等,其离面位移的测量灵敏度理论上可达到30 nm.数字散斑干涉属于全场测量,即能够获得被测物上任一点的变形/相对位移[5,9].
数字散斑干涉技术的光路有不同的类型,针对阵列式洛伦兹力微颗粒探测法的特殊应用,仪器采用了大剪切数字散斑干涉光路,使来自于被测悬臂梁和周边物体(即安装悬臂梁的横梁)的反射光发生干涉,形成剪切干涉.传统剪切电子散斑干涉技术的剪切量要远小于被测物体的尺寸,其测量的结果为物体位移的空间梯度;而本问题中剪切量大于被测物体尺寸,其测量结果直接为物体的位移,这种测量方法也叫大剪切电子散斑干涉技术.需要说明的是,相对于普通的数字散斑干涉光路,(大)剪切电子散斑干涉光路属于光学共路干涉,其抗干扰能力更强,光路可靠性更高,且对被测物体(包括横梁在内)的整体位移(即刚体位移)敏感度更低[18,19].
针对阵列式悬臂梁的大剪切数字散斑干涉技术测量离面位移的基本光路如图1所示.从激光器输出的光经扩束后照射到阵列式悬臂梁表面,漫反射光经过分光棱镜后分成两束光,分别经平面镜1和2反射后会聚到相机的图像传感器表面(图中的CCD阵列),形成干涉.其中平面镜2稍微倾斜,使得相机所得到的两幅图稍有错位,即实现剪切成像.当物体发生变形时,物体表面相邻两点的位移并不相同,由此产生的光程改变也不相同,即干涉信号的光程差发生变化,因此干涉信号的相位发生了变化.当测得干涉相位的变化量,即可得到相邻两点的位移差(近似于物体表面变形的梯度).而在本研究的大剪切数字散斑干涉系统中,由于参与干涉的参考光来自于固定的横梁,因此所测得的位移差即是悬臂梁的绝对位移[19−23].
数字散斑干涉法对悬臂梁位移测量过程如图2所示.
1)采集悬臂梁变形前后4幅散斑图,通过相移技术获得相应的相位图,再进行相位相减得到相位差,相关技术细节如下.
在悬臂梁变形前采集四幅剪切散斑干涉图,每一幅图的相位都比上一幅图的相位增加π/2,相移量的产生是由压电陶瓷作为驱动元件,推动平面反射镜移动来改变参考光的光程,四次的相移量分别是0,π/2,π,3π/2,则四幅干涉图的强度分布可以表示为:
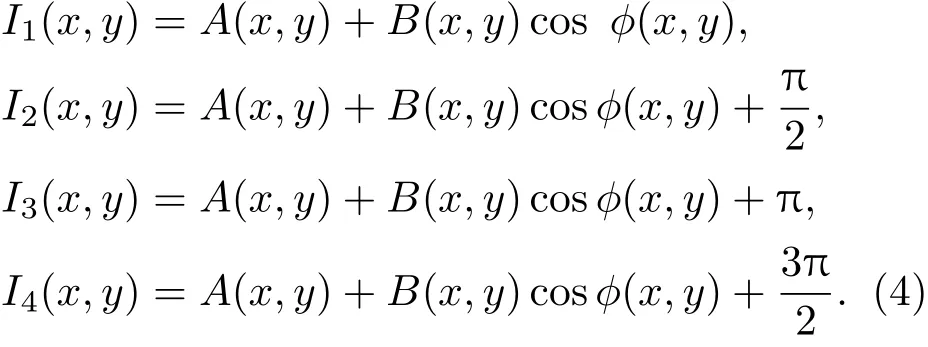
联立以上式子可得相位:
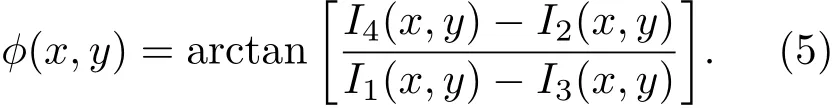
通过(5)式获得悬臂梁变形前的相位图.同理,采集悬臂梁变形后的4幅剪切散斑干涉图并计算出变形后的相位图,两相位图相减便可得到记录悬臂梁变形信息的相位差图.
2)悬臂梁位移量的获得
调节剪切量,使被测悬臂梁上一点和作为参考面的固定悬臂梁的横梁上一点发生干涉,则相位的变化可以表示为
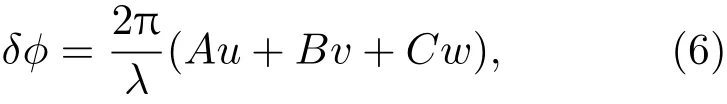
式中λ为光源;u,v,w分别为位移在x,y,z方向上的分量;A,B,C是对应于由几何关系决定的位移因子.实际光路中当激光器和相机位于xoz平面,相机位于被测物正前方,(6)式可以表示为
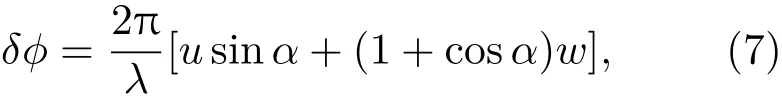
式中,α为照明方向与观察方向之间的夹角,实际光路中,当照明方向和观察方向基本一致时,α接近于0,则可通过(7)式求得离面位移量w.

即对得到的相位差图进行滤波,可以得到滤波后的相位差图,之后再对图像解包裹后便可进行三维显示,得到如(8)式所示的悬臂梁离面位移[11−15].
2.3 缺陷体积的获得
洛伦兹力微颗粒探测法前期研究工作中通过实验和数值模拟的方法获得了洛伦兹力变化量ΔF与悬臂梁位移量x之间的关系式

以及洛伦兹力变化量ΔF与缺陷体积V之间的关系式
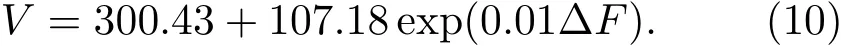
将通过电子散斑实验测量获得的悬臂梁位移量w代入(9),(10)式可获得缺陷体积V.
3 阵列式悬臂梁微变形实验及结果
如图1所示,激光器射出去的光经过扩束镜照射到阵列式排布悬臂梁表面,所产生的散射光被剪切散斑干涉仪记录;旋转台带动直径为50 mm的试样旋转,试样中存在一个深度0.5 mm、直径1 mm的圆柱状缺陷;缺陷经过阵列式探头某一永磁体电磁敏感区时使其对应的悬臂梁发生变形,通过搭建的电子散斑干涉平台对阵列式探头进行实时监测并输出结果,并将散斑干涉相位差转化为缺陷的体积信息.整个实验平台如图4所示.

图4 阵列式洛伦兹力微颗粒探测缺陷实验Fig.4.The Lorentz force particle analyzer setup with an array probe based on the shearography.
阵列式洛伦兹力探测法中含缺陷的待测试样与测量探头之间存在相对运动,实验中该相对运动是通过旋转电机实现,即将待测试样固定在电机上旋转多个周期,使含缺陷的试样周期性地通过测量探头,因此测量信号也是周期性重复出现,可利用信号的周期性对缺陷信号进行反复确认进而提高测量精度;进一步利用该特征,采用角度编码器检测旋转试样的角位移,每旋转一周输出特定个脉冲,经高速相机触发电路处理后形成特定时序的触发信号,使剪切电子散斑干涉测头里面的高速相机按特定逻辑时序进行散斑干涉图的采集,采用该方法使融合散斑干涉技术的阵列式洛伦兹力微颗粒探测法对高速相机的性能要求降低,但获得的悬臂梁位移量信息丰富.
如图5所示,阵列式探头由6个悬臂梁阵列排布构成,其测量敏感区宽度为10 mm,实验中直径为50 mm的试样以角速度ω旋转一周,可对直径差为10 mm范围内的试样部分进行扫描,阵列式探头单次扫描区域面积为图5中试样黑色区域所示,其值为2826 mm2;而一个永磁体悬臂梁结构中电磁敏感区宽度为1.5 mm,试样旋转一周,因此单探头单次扫描面积为463.9 mm2.可见本文提出的阵列式探头测量效率明显提高.
在悬臂梁变形前/后分别采集四幅剪切散斑干涉图,如图6所示.相对于图6(a),图6(b)中的剪切散斑干涉图包含了悬臂梁变形信息,但本文中变形量为微米级,从图6(a)及图6(b)剪切散斑干涉原始图中难以直接看出这个变化信息,因此需对剪切散斑干涉图处理进而获得悬臂梁变形前/后的相位图,如图7所示.
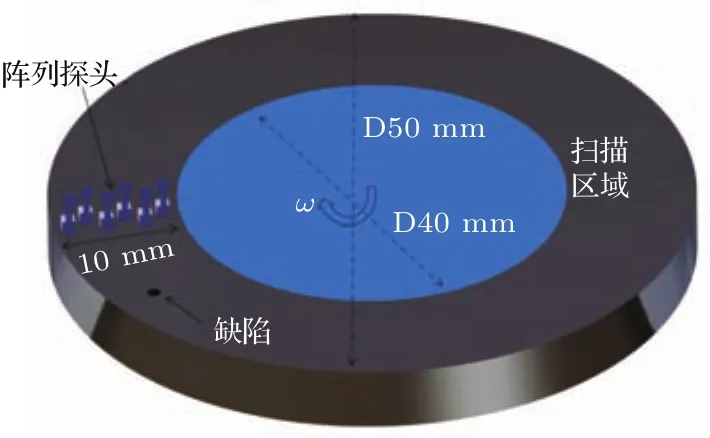
图5 阵列式探头扫描区域Fig.5.The electromagnetic sensing zone(EMSZ)of the array probe.

图6 悬臂梁变形前/后的4幅剪切散斑干涉图 (a)变形前;(b)变形后Fig.6.Four frames shearography images before(a)and after(b)the deformation of the cantilever.
对图7中变形前后的两相位图相减便可得到记录悬臂梁变形信息的相位差图,如图8所示.

图7 悬臂梁变形前/后的相位图 (a)变形前;(b)变形后Fig.7.Images of phase before(a)and after(b)the deformation of the cantilever.

图8 悬臂梁变形前后相位差图Fig.8.Image of phase di ff erence before and after the deformation of the cantilever.
之后对滤波后的相位差图解包裹后便可进行三维显示,得到发生变形的悬臂梁离面位移.图9所示为阵列式排布悬臂梁中受洛伦兹力作用的某一悬臂梁变形位移量.
如图9所示,在阵列式探头对试样进行扫描时,缺陷经过某一永磁体电磁敏感区域时其对应的悬臂梁发生了位移量,相比传统的三角法测量位移只能获得一个点的位移量,采用电子散斑方法获得了悬臂梁离面位移分布.前期实验和数值模拟获得的(9)和(10)式中位移值是悬臂梁末端的最大位移量,而图9中悬臂梁末端位移量为29.11µm,将该位移量代入(9)和(10)式可求得缺陷的尺寸为1.202 mm,而实际缺陷尺寸为1 mm.测量获得的缺陷尺寸与实际尺寸相差20%,造成这个测量误差的原因是表征洛伦兹力变化量与悬臂梁位移量(9)式和洛伦兹力变化量与缺陷尺寸(10)式是基于实验研究和数值仿真结果拟合得到的经验公式,存在一定的误差,但这个经验公式可通过后续的研究工作进行校准,进而逐渐提高缺陷尺寸的监测精度.因此本文通过实验验证了电子散斑方法应用于洛伦兹力微颗粒探测法中的可行性.
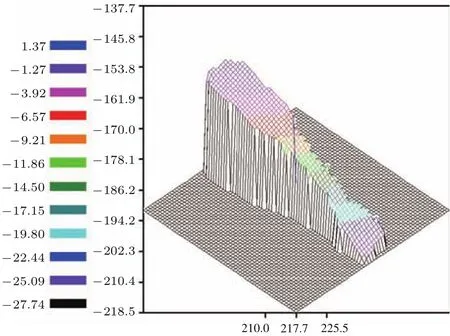
图9 (网刊彩色)悬臂梁受力变形位移图Fig.9.(color online)Full- fi eld displacement of cantilever caused by the fl aw.
阵列式探头由6个悬臂梁阵列排布构成,其测量敏感区宽度为10 mm,如图5所示,阵列式探头单次扫描区域面积为2826 mm2.实验结果表明在图5所示试样中,2826 mm2的扫描区域内存在尺寸为1.202 mm的缺陷1个.后续研究中可增加悬臂梁数量,设计电磁敏感区域更大的阵列式探头用于大面积试样的快速测量.
通过设计相关实验平台,独立开发了融合散斑干涉技术的阵列式洛伦兹力微颗粒探测法数据分析软件,并通过上述实验研究,以洛伦兹力及悬臂梁末端的位移量为中间量,建立了散斑相位差与缺陷体积之间的关系.但电子散斑的特征是全场特性,实验中也获得了悬臂梁各部位的离面位移分布,并且由洛伦兹力微颗粒原理部分可知缺陷的形状、裂纹方向可通过对其引起的洛伦兹力的力学特征信息分析获得,而要实现上述有挑战并且对工业应用有意义的研究工作,悬臂梁离面位移分布的获得是一个关键点,因为悬臂梁的离面位移分布与其受到的洛伦兹力方向及扭矩等力学参数相关.目前研究中尚未获得洛伦兹力与缺陷形状、裂纹方向等特征信息之间的关系,因此本文也仅通过悬臂梁末端位移量计算获得了缺陷的体积,后续的研究工作可在此基础上对悬臂梁离面位移分布进行分析,进而获得如缺陷形状、裂纹方向等特征参数.
此外课题组前期通过数值模拟研究获得20µm缺陷引起的洛伦兹力变化量为10−7N,在此量级力作用下即使对悬臂梁结构进行优化后,悬臂梁末端的最大位移量也仅为0.1µm,如果要获得悬臂梁位移曲线则需要测量分辨率至少在0.01µm量级,本文中采用的散斑干涉方法分辨率理论上可达30 nm,后续研究在此基础上有望探测到20µm级的缺陷.
4 结 论
提出了一种快速测量面积较大试样的阵列式探头,通过实验研究成功探测到了试样中的缺陷信息,验证了电子散斑应用到洛伦兹力探测法中的可行性.其中洛伦兹力微颗粒探测法相比于传统的无损检测方法,探测量电磁力为矢量,这一特性决定了可以通过对电磁力各分量进行分析而获得缺陷的体积、形状、裂纹的方向等特征信息,而电子散斑的全场测量特性决定了可以获得悬臂梁离面位移分布,因此本文工作也为获得缺陷形状、裂纹方向等特征信息奠定了基础.本文电子散斑法分辨率理论上可高达30 nm,进一步工作中对悬臂梁结构进行优化,有望探测到20µm级的缺陷.散斑干涉技术测量阵列式悬臂梁位移分布中的散斑干涉图分析软件为自主开发,目前还处于开发初期,一次完整实验并通过该软件系统获得悬臂梁位移分布图所需时间为30 min,需对该软件系统进一步开发,理想的测量时间应为5 min左右,在此基础上后续可对存在多个缺陷的试样进行监测研究,在上述几个方面进行深入研究,有望开发出一种实时、在线、原位的阵列式洛伦兹力微颗粒探测法.
[1]Sun M J,Liu T,Cheng X Z,Chen D Y,Yan F G,Feng N Z 2016Acta Phys.Sin.65 167802(in Chinese)[孙明健,刘婷,程星振,陈德应,闫锋刚,冯乃章 2016物理学报65 167802]
[2]Sun M J,Cheng X Z,Wang Y,Zhang X,Shen Y,Feng N Z 2016Acta Phys.Sin.65 038105(in Chinese)[孙明健,程星振,王艳,章欣,沈毅,冯乃章 2016物理学报 65 038105]
[3]Wu D H,Liu Z T,Wang X H,Su L X 2017Acta Phys.Sin.66 048102(in Chinese)[吴德会,刘志天,王晓红,苏令锌2017物理学报66 048102]
[4]Liu L,Meng G 2006Nondestruct.Test.28 28(in Chinese)[刘龙,孟光 2006无损检测28 28]
[5]GaoY,Fu S H,Cai Y L,Cheng T,Zhang Q C 2014Acta Phys.Sin.63 066201(in Chinese)[高越,符师桦,蔡玉龙,程腾,张青川2014物理学报63 066201]
[6]Wang X D,André T,Moreau R,Tan Y Q,Dai S J,Tao Z 2016J.Appl.Phys.120 188
[7]Moreau R,Tao Z,Wang X D 2016Appl.Phys.Lett.109 014903
[8]Li T,Wang Y L,Zhang J,Shi Y S 2015Appl.Opt.54 306
[9]Wang Y L,Shi Y S,Li T,Gao Q K,Xiao J,Zhang S G 2013Acta Phys.Sin.62 064206(in Chinese)[王雅丽,史祎诗,李拓,高乾坤,肖俊,张三国2013物理学报62 064206]
[10]Shi Y S,Wang Y L,Xiao J,Yang Y H,Zhang J J 2011Acta Phys.Sin.60 034202(in Chinese)[史祎诗,王雅丽,肖俊,杨玉花,张静娟2011物理学报60 034202]
[11]Shi Y S,Li T,Wang Y L,Gao Q K 2013Opt.Lett.38 1425
[12]Wu X Y,Yu Y J,Lü L J 2013Laser Optoelectr.Prog.50 18(in Chinese)[伍小燕,于瀛洁,吕丽军 2013激光与光电子学进展50 18]
[13]Wu X P,He S P,Li Z C 1980Acta Phys.Sin.29 1142(in Chinese)[伍小平,何世平,李志超 1980物理学报 29 1142]
[14]Wang X D,Yurii K,André T 2012Measur.Sci.Technol.23 045005
[15]Tan Y Q,Wang X D,Moreau R 2015Measur.Sci.Technol.26 035602
[16]Thess A,Votyakov E,Knaepen B,Zikanov O 2007New J.Phys.9 299
[17]Thess A,Votyakov E,Kolesnikov Y 2006Phys.Rev.Lett.96 164501
[18]Wu S J,He X,Yang L 2011Appl.Opt.50 3789
[19]Wu S J,Zhu L Q,Pan S Y,Yang L X 2016Opt.Lett.41 1050
[20]Wu S J,Zhu L Q,Feng Q B,Yang L X 2012Opt.Lasers Engineer.50 1260
[21]Li T,Shi Y S 2015Opt.Express23 21384
[22]Li T,Wang Y L,Zhang J,Shi Y S 2015Appl.Opt.54 306
[23]Li T,Shi Y S 2016J.Opt.18 035702
Lorentz force particle analyzer with an array probe based on speckle pattern interferometry∗
Dai Shang-Jun1)Wu Si-Jin2)Wang Xiao-Dong1)3)†Shi Yi-Shi1)3)‡
1)(School of Material Science and Opto-electronics Technology,University of Chinese Academy of Sciences,Beijing 100049,China)
2)(School of Instrumentation Science and Opto-electronics Engineering,Beijing Information Science and Technology University,Beijing 100192,China)
3)(Academy of Opto-electronics,Chinese Academy of Sciences,Beijing 100094,China)
5 May 2017;revised manuscript
17 July 2017)
A new contactless technique called Lorentz force particle analyzer(LFPA)with an array probe for detecting the flaws in metallic material is presented in this paper.Based on the principle of LFPA,the shape and size of the fl aw or the direction of the crack can be obtained by analyzing the pulses of the force acting on the permanent magnet.In the LFPA system,the small Lorentz force on the magnet is measured by a laser-cantilever system with high sensitivity,which operates in a similar principle to that of an atomic force microscope.The traditional displacement detecting method in the LFPA is not suitable for the array probe presented in this paper due to its complex structure.Therefore,speckle pattern interferometry is introduced into the LPFA.The speckle pattern interferometry can measure not only the out-of-plane displacement of the multiple cantilever in the array probe,or of slopes of deformation,but also the in-plane displacement.Those advantages make the speckle pattern interferometry a useful tool in the LFPA for analysing the shapes of the fl aws and the directions of the cracks.In this paper,a Michelson-type shear of graphic setup with enlarged angle of view is built to measure the displacement of the cantilever which is deformed by the fl aws in the sample.Four frames of shear under several grams before and after the deformation are captured and recorded by a digital camera.The phase di ff erence is processed for calculating the displacement with the software which is designed for the LFPA.A full- fi eld measurement of the cantilever displacement is achieved and the relationship between the phase di ff erence and the volume of the fl aws is also obtained successfully.The utilization of the speckle pattern interferometry technique in the LFPA leads to the invention of a new real-time,online,in-situcontactless technique of detecting the shapes of the internal fl aws and the directions of the cracks.
array,Lorentz force,speckle pattern interferometry,nondestructive detection
(2017年5月5日收到;2017年7月17日收到修改稿)
10.7498/aps.66.208102
∗国家自然科学基金(批准号:51374190)和中国科学院重大装备项目(批准号:YZ201567)资助的课题.
†通信作者.E-mail:xiaodong.wang@ucas.ac.cn
‡通信作者.E-mail:sysopt@126.com
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
PACS:81.70.Ex,81.70.Fy,07.60.LyDOI:10.7498/aps.66.208102
*Project supported by the National Natural Science Foundation of China(Grant No.51374190)and the Major Equipment Fund of Chinese Academy of Sciences(Grant No.YZ201567).
†Corresponding author.E-mail:xiaodong.wang@ucas.ac.cn
‡Corresponding author.E-mail:sysopt@126.com

