缓坡方程的非线性改进及其验证分析

江森汇+舒勰俊+侯堋

摘 要：弱非线性缓坡方程和弱非线性弥散关系不足以描述现有海洋波浪的非线性现象。在总结概述前人关于缓坡方程波浪数学模型的基础上，从Laplace方程出发，利用摄动展开方法推导出一强非线性缓坡方程，以此为控制方程，采用有限差分方法，并利用椭圆浅滩地形对强非线性缓坡方程进行了分析和探讨。结果表明，在椭圆浅滩前沿及两侧，计算精度比Maa（2002）的模式结果有所提高，与实验结果吻合较好，体现了非线性的作用。

关键词：缓坡方程 非线性 波浪变形

1.前言

Berkhoff最早根据势波理论采用小参数展开法，从Laplace方程出发导出了缓坡方程，称为传统缓坡方程，已被广泛应用于近岸海域的波浪场计算。目前，很多研究人员在考虑各种动力机制的情况下简化和改进了缓坡方程，并给出了一批拓展型缓坡方程。缓坡方程的改进大致可分为三类：一是对传统缓坡方程本身进行改进，如转化为抛物型缓坡方程或双曲型缓坡方程、考虑底摩阻作用、陡变地形作用、波浪破碎作用、波流相互作用等；二是对方程所采用的弥散关系进行改进，如Kirby、李瑞杰等都提出了各自的非线性弥散关系，使缓坡方程数学模型的计算结果大大改善；三是对求解缓坡方程的数值方法进行改进，如利用有限元法（FE）、共轭梯度算法（CG）、广义共轭梯度法（GCG）、高斯消去法（GE）等求解缓坡方程。

然而，以上的三类改进都是对缓坡方程的弱非线性作用进行改进。波浪由外海传播至近海时，由于受到水深、地形、建筑物等影响，非线性作用加强，弱非线性缓坡方程和弱非线性弥散关系不足以描述现有海洋波浪的非线性现象。本文在总结概述前人关于缓坡方程波浪数学模型的基础上，推导出一非线性缓坡方程，以此为控制方程，采用有限差分方法，并利用椭圆浅滩地形对改进后的缓坡方程进行了分析和探讨。

2.非线性缓坡方程的理论推导

从Laplace方程出发，利用摄动展开方法，在方程中乘以满足底部边界条件的水深因子，再由底部到水面沿水深积分，将三维问题简化为二维问题，推导得到强非线性缓坡方程，即本文的控制方程。下面简要说明推导过程，详细的推导过程见文献[13]。

考虑三维波浪场，假定流体不可压、无粘、运动无旋，其控制方程及边界条件分别如下所示：

拉普拉斯（Laplace）方程

在数值模拟过程中，采用具有二阶精度的五点式中心差分将控制方程和边界条件进行离散，再利用控制方程与边界条件的有限差分格式建立带状矩阵方程，并采用具有节约型带状矩阵解法功能的高斯消去法（GEP法）在PC机上直接求解椭圆型缓坡方程。

3.数值模擬验证及分析

为了观察推导出的非线性缓坡方程的适用性和计算结果的精度，采用Berkhoff的椭圆地形进行验证。通过数值试验，将改进后计算结果与Maa模式计算值及实验数据进行比较，探讨改进后模型的模拟精度。

Berkhoff椭圆具体水下地形和实测断面布置如图1所示。计算条件情况与原始实验相同，入射波高H0为0.0464m，入射波周期T为1.0s，入射方向为沿+x方向；x、y方向步长分别取为0.05m和0.1m；其它三边边界采用完全吸收边界。

图2分别给出了断面1～8的相对波高（H/H0）实验值、Maa等模式的计算值和改进模型计算值的比较图。从图2可以看出，断面1～5对C1值的改变的敏感程度不高，只是在局部位置存在波动，基本与Maa等模式重合；而断面6～8的计算值随C1值变化影响较大，尤其是在椭圆浅滩前沿及两侧处，C1值变大，出现振荡，呈现强非线性效应，拟合趋势优于Maa等模式，计算值更接近实验值。断面6～8在15m后面的区域，无论Maa等模式还是改进模型的计算值均有较大的偏差，其原因可能是由于模型未考虑底摩阻和波浪破碎的影响，而使得计算值较实测值偏大。尽管在个别断面上存在一定误差，还有变差的趋势，但整体上模型的计算结果的计算精度相比Maa等模式有所提高，与实验结果吻合较好，体现了强非线性的作用。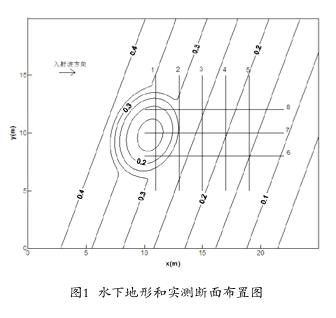

4.结语

针对缓坡方程弱非线性的局限性，利用摄动展开方法推导出一强非线性缓坡方程，并采用椭圆浅滩地形验证其计算精度。将模拟结果和Maa等模式计算结果及实验数据进行比较，结果表明，在椭圆浅滩前沿及两侧，计算结果出现振荡，与实验结果吻合较好，计算精度相比Maa等模式有所提高，呈现出非线性效应。在推导出的非线性缓坡方程中存在待定系数C1，假定C1值为常系数，通过选取不同的C1值得到的模拟结果与实验数据的比选，分析C1值对非线性性能的影响，确定最佳C1值。随着C1值的增大，非线性加强，可能导致计算结果失真，以后将进一步讨论其与波高、波长和水深等因素的函数关系及其物理意义。

参考文献：

[1]Berkhoff J C W. Computation o f c o m b i n e d r e f r a c t i o n -diffraction[A].In Proc. 13th Int.Conf.on Coastal Engineering[C]. ASCE，1972，471-490.endprint