围长至少为6的曲面图的列表单射染色

陈宏宇，戚建明

(1.上海应用技术大学 理学院，上海 201418；2.上海电机学院 文理教学部，上海 201306)

围长至少为6的曲面图的列表单射染色

陈宏宇1，戚建明2

(1.上海应用技术大学 理学院，上海 201418；2.上海电机学院 文理教学部，上海 201306)

嵌入图；列表单射染色；围长

图G的点染色称为单射的，如果任何有公共邻点的两个顶点染不同颜色.设χi(G)表示G的单射染色中的最小颜色数.显然，Δ(G)≤χi(G)≤|V(G)|.

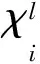
单射染色是由Hahn等[2]在2002年引入的.他们证明了若G是连通图，且G≠K2，则χ(G)≤χi(G)≤Δ2(G)-Δ(G)+1.下面是关于单射染色的一些已知结果.

定理1设G是最大度为Δ的图.

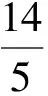
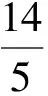
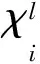
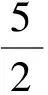
文献[6-11]给出了在围长和最大度的条件限制下单射染色问题的一些结论.

定理2设G是g(G)≥g′且Δ(G)≥D的平面图.

(1) 若(g′，D)∈{(13，4)，(10，6)，(8，10)，(7，16)}，则χi(G)=Δ.

(2) 若(g′，D)∈{(9，4)，(8，15)，(7，7)，(6，18)}，则χi(G)≤Δ+1.

(3) 若(g′，D)∈{(7，1)，(6，14)，则χi(G)≤Δ+2.

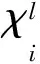
2010年，Lužar[12]提出了如下猜想.若此猜想成立，则其上界是紧的.

猜想A设G是最大度为Δ的平面图.

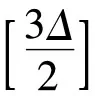
本文，我们将证明如下结果.

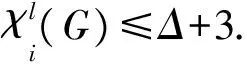
下面介绍本文中用到的一些定义及符号.

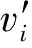
显然，在G中与点v有公共邻点的顶点的个数最多是SG(v).所以，如果除v外其余顶点都被单射染色，则点v最多有SG(v)种可限制的颜色.

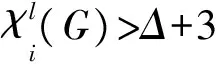
设G=(V，E，F)是嵌入到欧拉示性数非负的曲面上的图.定义ω为初始值.对每个点v∈V(G)，设ω(v)=2d(v)-6，每个面f∈F(G),ω(f)=d(f)-6.由欧拉公式|V|-|E|+|F|=χ(Σ)，有

(1)

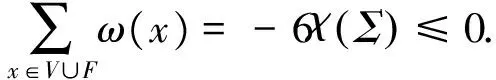
(2)

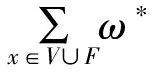
引理1δ(G)≥2.

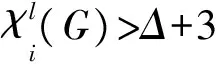
引理2设uv∈E(G)，则max{SG(u),SG(v)}≥Δ+3.

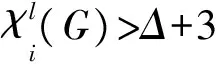
引理3设d(v)=3,N(v)={v1,v2,v3}.若d(v3)=2,则max{d(v1),d(v2)}≥6.

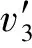
引理4G不存在相邻的2-点.

证 假设u,v是两个相邻的2-点.因为SG(u)≤Δ<Δ+2,SG(v)≤Δ<Δ+2,与引理2矛盾.

引理5设3≤d(v)≤4,则n3+(v)≥2.

证 假设n3+(v)≤1，即v与最多一个3+-点相邻.设ω是与v相邻的一个2-点.如果n3+(v)=0，则n2(v)=d(v).所以，SG(v)=2n2(v)-d(v)=d(v)<Δ,SG(ω)≤d(v)+Δ-2.又因为d(v)≤4,故SG(ω)≤Δ+2,与引理2矛盾.如果n3+(v)=1,设u是v的3+-邻点.则SG(v)=d(u)+2(d(v)-1)-d(v)=d(u)+d(v)-2≤d(u)+2≤Δ+2,SG(ω)≤d(v)+Δ-2≤Δ+2,与引理2矛盾.

定义下面的赋值方案.

首先根据点v的度，分6种情况来证明对于每个点v∈V(G)，有ω*(v)≥0.

情况1d(v)=2.由引理4，v有两个相邻的3+-点.因此，由R1，ω*(v)=2d(v)-6+2=0.

情况2d(v)=3.由引理5，n2(v)≤1.若n2(v)=0,则v不给它的邻点任何值，所以，ω*(v)≥2d(v)-6=0.如果n2(v)=1,即d(v3)=2,d(v1)≥d(v2)≥3.则根据引理3，d(v1)≥6.由R1，R2得，ω*(v)≥2d(v)-6-1+1=0.

情况3d(v)=4.由引理5，n2(v)≤2.由R1，ω*(v)≥2d(v)-6-2×1=0.

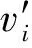
情况5 6≤d(v)≤Δ-1.由R1，R2，v最多给每个相邻的3--点1.所以，ω*(v)≥2d(v)-6-d(v)×1≥0.

设ω是v的任意一个邻点，ξv ω表示点v沿边vω给出的值的总和.

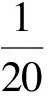
下面，对于每个面f∈F(G)来证明ω*(f)≥0.

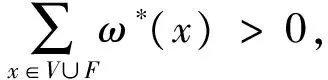
[1] BONDY J A,MURTY U S R.Graph theory with applications [M].New York：North-Holland,1976.

[2] HAHN G,KRATOCHVI J,SIRJ,etal.On the injective chromatic number of graphs [J].DiscreteMath,2002,256(1-2)：179-192.

[3] DOYON A,HAHN G,RASPAUD A.Some bounds on the injective chromatics number of graphs [J].DiscreteMath,2010,310(3)：582-590.

[4] CRANSTON D W,KIM S J,YU G.Injective colorings of phanar graphs with low average degree [J].Algorithmica,2010,60：553-568.

[5] LI R,XU B.Injective choosability of planar graphs of girth five and six [J].DircreteMath,2012,312：1260-1265.

[6] CRANSTON D W,KIM S J,YU G.Injective colorings of sparse graphs [J].DiscreteMath,2010,310：2965-2973.

[7] BORODIN O V,IVANOVA A O.List injective colorings of planar graphs [J].DiscreteMath,2010,311(2-3)：154-165.

[8] BORODIN O V,IVANOVA A O.Injective (Δ+1)-colorings of planar graphs with girth 6 [J].SiberianMathJ,2011,52：23-29.

[9] BU Y H,LU K.Injective coloring of planar graphs with girth 7 [J].DiscreteMathAlgorithmAppl,2012,4(2)：1-8.

[10] BU Y H,LU K.List injective coloring of planar graphs with girth 5,6,8 [J].DiscreteApplMath,2013,161(10)：1367-1377.

[11] BU Y H,YANG S.List injective coloring of planar graphs with girthg≥5 [J].DiscreteMathAlgorithmAppl,2014,6(1)：1-12.

[12] LUŽAR B.Planar graphs with largest injective chromatic numbers [J].IMFM,2010,48: 1110.

TheListInjectiveColoringofEmbeddedGraphswithGirthatLeastSix

CHENHongyu1,QIJianming2

(1.SchoolofScience,ShanghaiInstituteofTechnology,Shanghai201418,China;2.DeparmentofMathematicsandPhysics,ShanghaiDianjiUniversity,Shanghai201306,China)

A vertex coloring of a graphGis called injective if any two vertices with a common neighbor

embedded graph; list injective coloring; girth

0427-7104(2017)05-0523-04

2016-03-28

国家自然科学基金青年基金(11401386)；上海电机学院学科建设项目(16JCXK02)

陈宏宇(1981—)，女，副教授，博士，E-mail：hongyuchen86@163.com.

O5；C15

A