含漂移项分数布朗运动方差估计量的Edgeworth展开

司成杰

(武汉大学数学与统计学院, 湖北 武汉 430072)

含漂移项分数布朗运动方差估计量的Edgeworth展开

司成杰

(武汉大学数学与统计学院, 湖北 武汉 430072)

对含漂移项分数布朗运动方差估计量进行研究. 在胡耀忠等人已有工作的基础上, 对方差的极大似然估计量的三、四阶原点矩进行计算, 并在矩的基础上得到相应的累积量, 最后给出标准化后的方差估计量所满足的三项局部Edgeworth展开项.

极大似然估计；原点矩；累积量；Edgeworth展开

0 引言

长记忆过程在金融、生物、信号网络等领域有着非常广泛的应用. 分数布朗运动也是一类特殊的长记忆过程(H>1/2). 关于分数布朗运动的随机积分也已经有了较为完善的研究[1-2]. 当利用长记忆过程描述某些具体现象时, 确定模型中相关参数就显得尤为重要. 本文中主要研究含漂移项分数布朗运动线性模型

Xt=μt+σBH(t)

(1)

其中μ和σ是需要通过过程X的离散观测样本来进行估计的参数, {BH(t),t≥0}是Hurst参数H∈(0,1)的分数布朗运动(不考虑H=1/2情形). 假设过程经由离散时间(t1,t2,…，t,tN)观测. 为方便起见, 取tk=kh,k=1,2,…,N. 这样观测过程序列X=(Xt1,Xt2,…,XtN).

之所以选择研究模型(1)是因为其具有实际意义和应用性. 关于含漂移项时Hurst参数的参数估计在[3-5]中有了较为深入的研究, 其中最为著名的一种Hurst参数估计就是R/S估计. 此外, 在金融中很热门研究的几何分数布朗运动, 也是来源于模型(1). 基于连续时间观测样本的分数O-U过程中参数估计[6]也与模型(1)有着密不可分的关系.

胡耀忠等[7]给出了模型(1)在离散样本下即观测时间序列t=(h,2h,…,Nh)′和分数布朗运动序列BH(t)=(BH(h),BH(2h),…,BH(Nh))′条件下, 参数σ2的极大似然估计[8]

(2)

其中MH是协方差矩阵, 具体形式

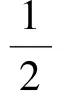
(3)

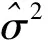
1 预备知识

定义1.1随机变量X的特征函数定义为C(t)=E(eitX), 特征函数与矩存在如下关系

与矩类似,X的累积量Γk是特征函数取对数后的展开式系数

前4阶累积量与矩对应关系如下

引理1.1假定{Zi}是一组均值和方差分别为μ和σ2. 记Xn为其标准和

(4)

若记Fn为随机变量Xn的分布函数. 对序列Xi, 其均值、方差、r阶累积量依次为μ、σ2和σrΓr. 则其前几项Edgeworth展开项满足

(5)

其中Φ(x)表示标准正态分布的分布函数,Φ(3)(x)表示Φ(x)关于x的三阶求导.

引理1.1是最为常见的Edgeworth展开项形式, 由Cramér[9]于1928年证明展开项级数关于x一致存在, 且前三项的局部展开误差为ox(n-1).

2 方差估计量的三、四阶原点矩

(6)

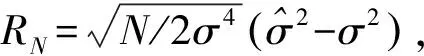
(7)

(8)

引理2.1的证明利用胡耀忠[7]通过高斯构造法得到的等式(α≠1/2)

(9)

将(9)式左右两端分别作泰勒展开并比较系数, 有

(10)

即证明了(7)式成立. 再将(10)式结果带入到RN的三阶原点矩计算, 即有(8)式成立. 证毕.

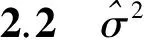
(11)

(12)

引理2.2的证明与引理2.1证明过程类似, 只需计算得到

将上述结果带入相应的原点矩计算公式即可. 证毕.

3 方差估计量的三、四阶累积量与Edgeworth展开

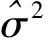
(13)

(14)

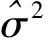
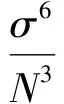
(15)

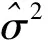
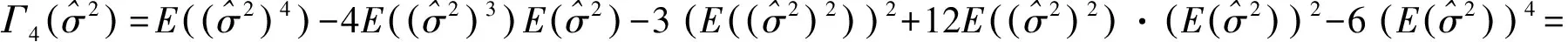
(16)

证毕.

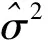
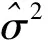
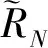
(17)

(18)

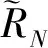
E(RN)3-3E(RN)E(RN)2+2(E(RN))3=

(19)

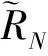
E(RN)4-4E(RN)E(RN)3+6E(RN)2(E(RN))2-3(E(RN))4=

(20)

证毕.

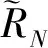
(21)

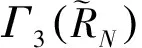
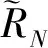
(22)

致谢：非常感谢审稿人的审稿意见, 也非常感谢导师高付清老师的选题与指导.

[1] Biagini F, Hu Yaozhong, ksendal B, et al. Stochastic calculus for fractional brownian motion and applications[M]. New York: Spring, 2008.

[2] Feller W. An introduction to probability theory and its applications[M].3rd ed. New York: Wiley, 1969.

[3] Beran J. Statistics for long-memory processes[M]. New York: Chapman and Hall, 1994.

[4] Fox R, Taqqu M S. Large-sample properties of parameter estimates for strongly dependent stationary gaussian time series[J]. Ann Statist, 1986, 14(2): 517-532.

[5] Hannan E J. The asymptotic theory of linear time-series models[J]. J Appl Probability, 1973, 10(1): 130-145.

[6] Hu Yaozhong, David N. Parameter estimation for fractional Ornstein-Uhlenbeck processes[J]. Statistics Probability Letters, 2010, 80(11/12): 1030-1038.

[7] Hu Yaozhong, David N, Xiao Weilin, et al. Exact maximum likelihood estimator for drift fractional Brownian motion at discrete observation[J]. Acta Math Sc, 2011, 31(5): 1851-1859.

[8] Shao Jun. Mathematical statistics[M].2nd ed. New York: Springer, 2003.

[9] Cramér H. On the composition of elementary errors[J]. Skand Aktuarietidskr,1928(11): 13-74.

[10] David N, Salvador O L. Central limit theorems for multiple stochastic integrals and Malliavin calculus[J]. Stoc Proc Appl, 2008, 118(4): 614-628.

[11] Fujikoshi Y, Ulyanov V V, Shimizu R. Multivariate statistics: high-dimensional and large-sample approximations[M]. New York: Wiley, 2009.

Edgeworthexpansionofvarianceestimatorfordriftfractionalbrownianmotion

SI Chengjie

(School of Mathematics and Statistics, Wuhan University, Wuhan 430072,China)

This article is mainly about the variance estimation for drift fractional brownian motion. Based on maximum likelihood estimator from the work of Hu Yaozhong, etc., we computed the third and forth moments of the estimator, and also it was cumulants, then we claimed the Edgeworth expansion series for the variance estimation.

maximum likelihood estimator; moment; cumulant; Edgeworth expansion series

2017-05-15

司成杰(1992-)，男，硕士生，E-mail:740909911@qq.com

1000-2375(2017)06-0563-04

X36

A

10.3969/j.issn.1000-2375.2017.06.001

(责任编辑 赵燕)