双层规划模型在导弹破片杀伤战斗部优化设计中的应用*
余丽山,李彦彬,金学科,翟夕阳
(空军工程大学防空反导学院,西安 710051)
双层规划模型在导弹破片杀伤战斗部优化设计中的应用*
余丽山,李彦彬,金学科,翟夕阳
(空军工程大学防空反导学院,西安 710051)
破片杀伤战斗部结构设计考虑因素众多复杂,为梳理战斗部设计中各层次之间的关系,改善导弹的性能,文中综合考虑了战斗部的威力以及导弹的机动性能。文中分别用战斗部的威力半径、导弹重量表征战斗部的威力和导弹的机动性能,建立了战斗部结构参数优化设计的双层规划模型。为避免求解过程中陷入局部最优,提出了模拟退火算法对模型求解。最后用算例得到了战斗部的最优结构参数,证明了模型和算法的有效性。
破片杀伤战斗部;威力半径;优化设计;双层规划模型;模拟退火算法
0 引言
战斗部是地空导弹的重要组成部分,战斗部的设计也影响和制约着导弹总体的设计[1]。关于战斗部的设计,是指在满足导弹威力指标要求下,同时考虑导弹总体性能要求综合集成和不断优化的过程。进行设计时需要综合考虑战斗部装药类型、结构参数、起爆方式以及导弹总体质量与机动性等多个因素,且各个因素之间互相影响。传统的导弹战斗部设计方法是首先进行战斗部结构设计,然后基于相关实验对参数进一步优化。这种设计方法研制周期长、花费巨大且不利于得到系统规律性数据,难以获取最优且便于工程实现的战斗部结构设计参数[2]。因此需要建立科学合理的导弹战斗部设计模型,综合分析各因素之间的层次关系。
针对导弹战斗部结构设计与优化,通常采用理论分析、数值模拟及试验等方法。如石志彬[3]等通过假设战术弹道导弹目标的相关参数,进行理论分析来优化战斗部的主要结构参数;丁建超[4]等通过仿真找出影响导弹动能杆战斗部杀伤概率的主要因素,以杀伤概率、战斗部质量为目标函数建立优化模型,指导战斗部的优化设计;李伟兵[5]等,对不同起爆条件下战斗部的威力采用理论分析的手段,然后数值模拟优化战斗部装药的结构参数,最后通过试验验证仿真结果,得到地空导弹战斗部的最优结构。文中针对地空导弹破片杀伤战斗部优化设计问题,综合考虑了战斗部威力和导弹机动性能,建立了关于战斗部结构参数设计的双层规划模型,并根据模型提出了模拟退火算法对其求解。
1 双层规划模型
双层规划模型主要研究的是具有相互作用的两个不同目标函数之间的关系。上层目标函数较下层目标函数具有优先权,下层目标函数随着上层目标函数的改变而改变,并作出适合自己的选择。由于两方的行为相互干扰影响,并且其中一方的选择又不能完全影响另一方的选择,所以上层目标函数要根据下层目标函数的选择最终作出最有利于自己的决定[6]。战斗部的设计应该首先满足战斗部对目标的杀伤能力。其次,战斗部的重量在很大程度上影响着导弹总体的重量,为避免影响导弹的机动性能,必须保证战斗部的重量不能太大[7]。文中采用双层规划模型来描述战斗部威力与战斗部重量之间的相互关系,从而优化战斗部的设计。
1.1 破片战斗部威力分析
假设地空导弹战斗部的破片为活性破片,与传统的金属破片不同。为保证爆炸的安定以及破片结构的完整,需要在破片与炸药之间安装缓冲层,针对图1简单陈述活性破片战斗部结构[8]。
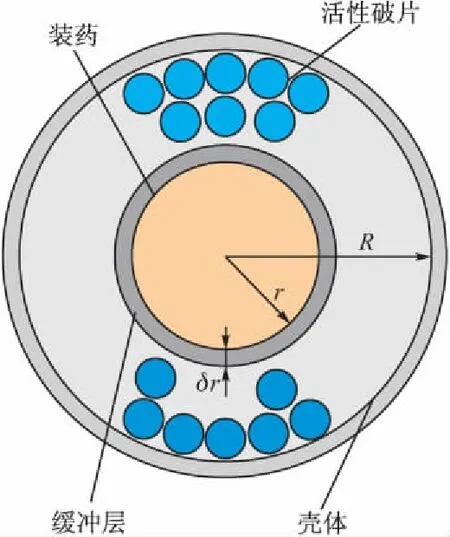
图1 活性破片战斗部结构
假设战斗部破片的参数集合为F:
(1)
式中:战斗部破片的质量、速度、飞散角以及方向角分别用m0、v、φ、β表示。
活性破片必须满足两个条件,才能够对目标进行毁伤:①破片具有足够穿透目标表层的动能;②破片穿透目标表层后能够引起爆炸。这就表明:
Ek≥Ey1
(2)
Ek≥Ey2
(3)
Ek、Ey1、Ey2分别表示活性破片的碰撞动能、活性破片击穿目标表层所需的动能以及临界起爆压力所对应的活性破片撞击动能。则破片的杀伤准则为:
(4)
式中Ey=max(Ey1,Ey2)。
为了对目标进行毁伤,破片不仅需要满足杀伤准则,而且还要符合空间分布密度准则。
此时,战斗部对目标的杀伤概率为:
Pn=1-eρSP
(5)
式中:ρ表示活性破片的空间分布密度;S表示暴露在破片场中目标的易损面积。P表示单枚破片的杀伤概率。由式(5)可知,战斗部对目标的杀伤概率与破片的空间分布密度ρ以及单枚破片的杀伤概率P有关,且这两个因素相互制约。
当战斗部质量一定时,若破片的空间分布密度ρ增加,即破片的数量N增加,则单枚破片的质量m0减少,碰撞动能Ek就会减小,对应的单枚活性破片的杀伤概率P就会减小。由于战斗部的作用距离影响着活性破片的碰撞动能Ek和破片的空间分布密度ρ,并且Ek和ρ变化趋势相反,因此可用战斗部的威力半径D来表征战斗部的威力,其中D是关于活性破片的碰撞动能Ek和破片的空间分布密度ρ的综合性函数。
1.2 上层规划模型
根据图1,假设m表示战斗部的重量,r表示装药半径,缓冲层厚为装药半径的δ倍,R表示战斗部半径,装药、缓冲层、活性破片对应的密度分别为ρ0、ρ1、ρ2。假设导弹在飞行过程中,空气对战斗部壳体的影响忽略不计,那么装填比α为:
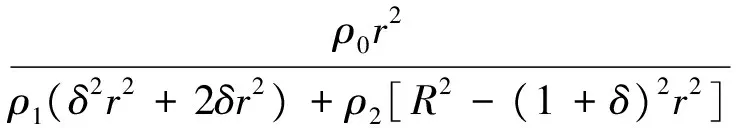
(6)
活性破片的初速度为:

(7)
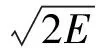
根据对目标进行毁伤的动能Ey,活性破片的最终速度vf为:

(8)
破片在飞行的过程中,速度因受空气阻力的影响而衰减。设空气阻力系数为C,空气的密度为ρa,形状相同时,钢质破片的形状系数为φ,那么衰减系数θ为:
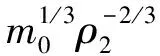
(9)
若满足动能要求对目标进行毁伤,战斗部的最大杀伤距离D1为:
(10)
活性破片的数量Ne为:
(11)
若满足空间分布密度ρ的要求对目标进行毁伤,战斗部的最大杀伤距离D2为:
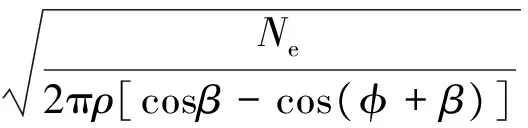
(12)
那么,战斗部的威力半径D为:
D=min(D1,D2)
(13)
若D1=D2,则可以得到同时满足动能要求和密度分布准则的威力半径D,即:
(14)
目标函数:maxD
活性破片战斗部在设计时,应该首先考虑是否满足搭载平台的发射条件,即必须对战斗部的质量、结构参数进行限制。
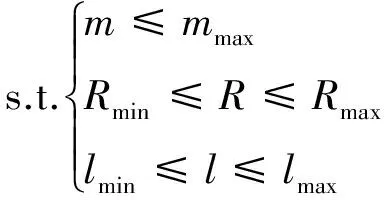
(15)
1.3 下层规划模型
为了改善导弹的机动性能以及增大导弹的射程,要求导弹的质量尽可能的小。
导弹的总质量M为:

(16)
式中:M表示导弹的总质量;mk表示控制系统的质量;KPP表示动力系统相对质量系数;KS表示弹体结构相对质量系数。经过统计[9],m/M≈0.1~0.2,平均统计值集中在0.14~0.15。因此,为保证导弹的总质量尽量的小,战斗部的质量也必须尽量的小。
目标函数:minm
m=mz+mh+mp
(17)
(18)
式中:mz、mh、mp分别表示战斗部装药、缓冲层、破片的质量;l表示战斗部的长度。
基于对导弹战斗部设计要求,要求战斗部各结构参数在一定范围内变化。
(19)
2 模拟退火算法
模拟退火算法(SA)是一种适合解决组合模型的人工智能算法。它可以在算法的搜索过程中,有效的避开局部最优解,并使目标函数最终稳定在全局最优解处[10]。双层规划问题是一个NP-hard问题,为避免在求解过程中陷入局部最优,可使用模拟退火算法对其求解。
2.1 算法具体步骤
依据模拟退火算法,对战斗部优化设计的双层规划模型的求解算法进行设计。
第一步 初始化。设定战斗部初始的结构参数i0,将i0代入下层目标函数进行求解,得到战斗部质量m0,将m0代入上层目标函数,得到最终的战斗部威力半径D0。分别确定内层循环次数e,循环的初始温度T0以及终止温度Tf,然后令外层循环次数n=0,即Tn=T0。
第二步 对于温度Tn可进行如下步骤:
①令内层循环次数k=1。
②产生新的状态,即根据战斗部的威力半径D0,选择其他的结构参数i1。
③将i1代入下层目标函数进行求解,得到m1(新的结构参数下战斗部的质量)。将m1代入上层目标函数,得到战斗部质量为m1时,战斗部的威力半径D1。
④令Δf=D0-D1,由于威力半径D越大越好,若Δf<0,接受i1(接受该结构参数);若Δf>0,依据概率来决定是否接受i1。是否接受i1的方法:产生一个随机数ε=U(0,1),计算exp(-Δf/T),T是目前温度,若exp(-Δf/T)>ε,就接受该结构参数。
⑤若k=e,接下来转第三步;若k=k+1,返到第二步。
第三步 判断循环是否终止。若Tn 2.2 模拟退火算法流程图 图2 模拟退火算法流程图 以战斗部结构参数优化设计为例,兼顾战斗部的威力半径以及战斗部的质量,运用以上限制因素,通过Matlab编写模拟退火算法程序,得到战斗部的威力半径和战斗部质量迭代次数分别如图3和图4所示。 图3 威力半径迭代次数 图4 重量迭代次数 由上图可知,战斗部的威力半径和战斗部的质量迭代334次时趋于稳定,并稳定在全局最优处。基于战斗部设计的要求,选取3组有代表性的数据如表1所示。 表1 战斗部结构参数 通过对上表分析可知,当战斗部结构参数在较小范围内变化时,战斗部的威力半径增加,质量显著下降。其中,第3组结构参数最优,此时战斗部的质量最小,威力半径最大。 文中从破片杀伤战斗部设计时对威力半径和质量的要求不同进行了研究。建立了双层规划模型来对战斗部的结构参数进行优化设计。为避免求解过程中陷入局部最优,使目标函数快速稳定在全局最优处,提出了模拟退火算法对模型求解。最后,通过算例得到了战斗部的最优结构参数,此时战斗部的质量为7.74 kg,战斗部的威力半径为12.0 m。经过文中的仿真计算,表明了模型和算法可有效用于战斗部结构参数优化设计问题。 [1] 蒋浩征,周兰庭,蔡汉文.火箭战斗部设计原理 [M].北京:国防工业出版社,1982:1-5. [2] 毛亮,姜春兰,王超.基于改进遗传算法的破片杀伤战斗部优化设计 [J].兵工学报,2015,36(3):457-458. [3] 石志彬,高敏,杨锁昌,等.瞄准式战斗部杀伤装置结构设计研究 [J].兵工学报,2013,34(3):373-377. [4] 丁建超,王朝志,陈万春.反TBM导弹动能杆战斗部优化设计 [J].战术导弹技术,2005(4):7-11. [5] 李伟兵,樊菲,王晓鸣.杆式射流与射流转换的双模战斗部优化设计 [J].兵工学报,2013,34(12):1500-1505. [6] 邸振,饶三平.常规公交线网运力配置双层规划模型 [J].南昌大学学报,2013,37(4):330-333. [7] 韩晓明,高峰.导弹战斗部原理及应用 [M].西安:西北工业大学出版社,2012:1-8. [8] 余庆波,刘宗伟,金学科.活性破片战斗部威力评价方法 [J].北京理工大学学报,2012,32(7):661-664. [9] 韩晓明,李彦彬,邓建军.地空导弹总体设计原理 [M].西安:空军工程大学导弹学院,2009:47-52. [10] 常成.基于改进的模拟退火算法的电力市场最优潮流分析 [J].贵州师范大学学报,2015,33(4):83-86. ApplicationofBi-levelProgrammingModelinOptimizationDesignofMissileFragmentingWarhead YU Lishan,LI Yanbin,JIN Xueke,ZHAI Xiyang (Air and Missile Defense College,Air Force Engineering University,Xi’an 710051,China) Many complex factors should be considered for fragmenting warhead structure design.To rationalize the relationship between various levels in design of warhead and improve performance of missile,the power of the warhead and missile motor performance were taken into account in comprehensive.Power radius of the warhead,weight of the missile were used to replace power of warhead and missile motor performance and the bi-level programming model of the warhead structural parameters optimization design was established.To avoid the process of solving the model into local optimum,simulated annealing algorithm was adopted to solve the model.At last,the example was used for optimal warhead structural parameters and validity of the model and algorithm was proved. fragmenting warhead; power radius; optimization design; bi-level programming model; simulated annealing algorithm 10.15892/j.cnki.djzdxb.2017.02.017 2016-05-24 余丽山(1992-),男,湖北孝昌人,硕士研究生,研究方向:国防采办与项目管理。 TJ410.2 A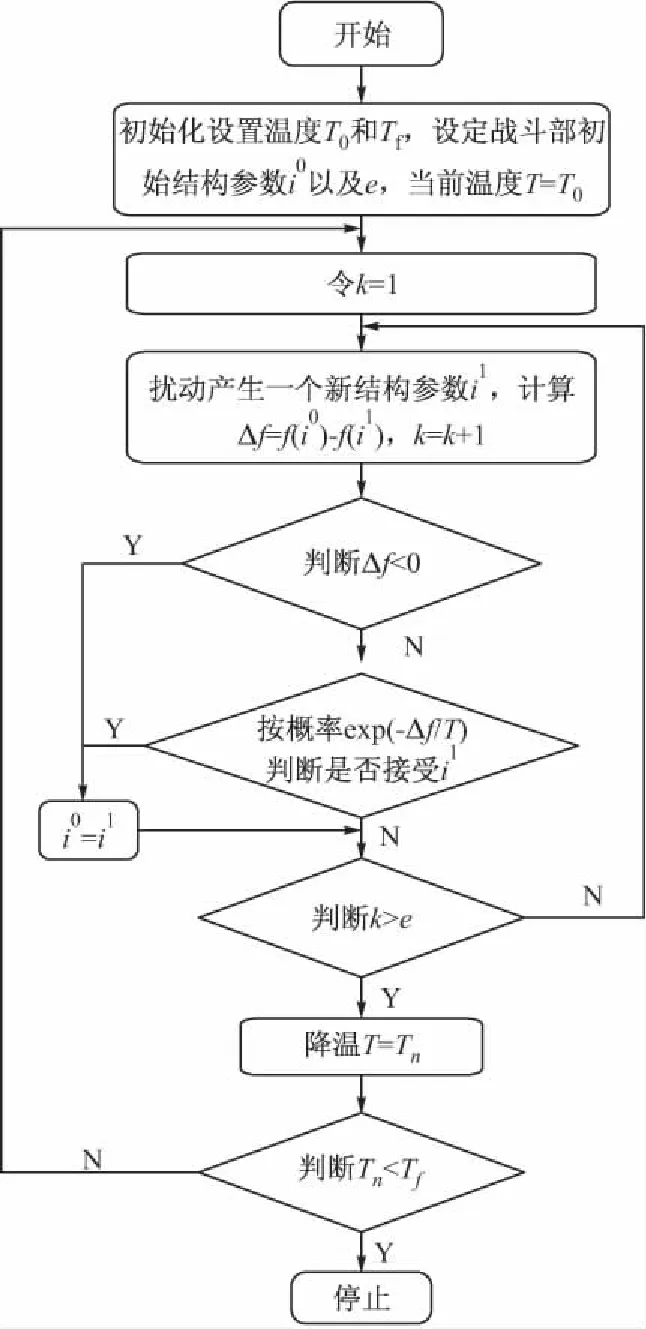
3 算例分析
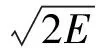
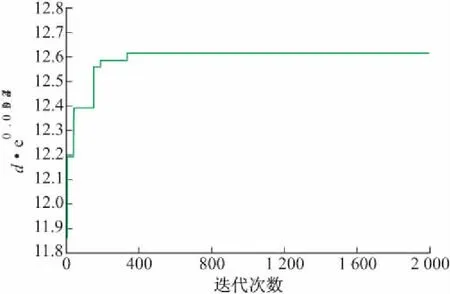
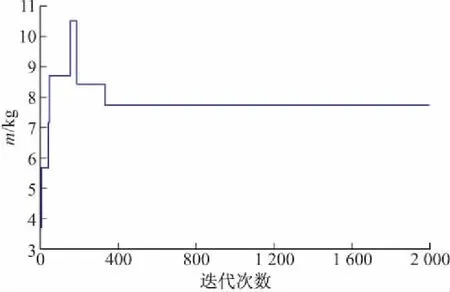
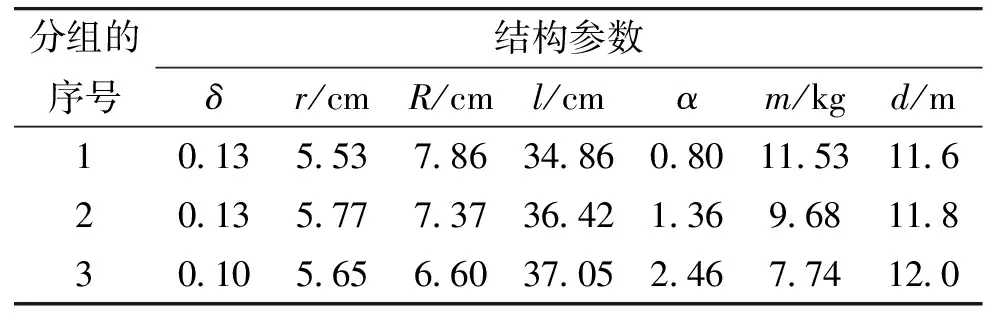
4 结论

