一种可变形桁架避障规划方法*
邓 雅,王泽国,张锦江
(北京控制工程研究所,北京 100190)
*国家重点基础发展计划资助项目(2013CB733100).
一种可变形桁架避障规划方法*
邓 雅,王泽国,张锦江
(北京控制工程研究所,北京 100190)
为解决VGT的避障规划问题,给出一种等效机械臂模型并分析单级VGT正向递推运动学中的冗余问题.针对等效模型,利用遗传算法设计避障规划算法得到等效模型变量,再反算VGT各级可调杆长度得到VGT的避障算法.所得结果使得VGT等效机械臂模型各级具有相同的移动关节长度,且相邻两级转动关节角度变化较小.对避障规划结果和VGT到等效模型的变换进行仿真验证对比,验证算法有效性.
可变形桁架;避障规划;遗传算法;等效机械臂模型
0 引 言
可变形桁架(VGT)的空间结构确定而几何参数可变,通过调节部分杆件的长度来实现对末端负载位置和姿态的移动[1].VGT一般具有更多的自由度,因而与空间机械臂相比,具有更强的灵活性[2-3].VGT可以安装在国际空间站等大型航天器上,由于大型航天器具有复杂的结构,VGT在执行空间任务中,需要特别考虑避障规划问题.
针对VGT的设计和控制等问题开展了众多研究工作.文献[4]研究了VGT最优构型问题.文献[5]分析了国际空间站上桁架的性能.文献[6]给出了一种慢速运动下的轨迹跟踪方法.文献[7]采用自适应结构的思想,研究了航天器搭载多个VGT时的动量管理问题.
机器人的避障规划问题也已有许多研究成果.文献[8-11]给出了机器人避障运动规划中一些经典算法的详细介绍,如路标规划法、广义势场法、空间分割法等.但是这些方法并没有给出针对桁架系统的算法,不能直接应用于桁架系统.文献[12]考虑可调杆具有离散状态的VGT模型,利用逆运动学和空间分割法设计了避障规划算法.该方法需要离线存储大量数据,VGT的逆运动学求解需要大量计算,并且仅适用于具有离散状态的可调杆,算法设计比较复杂.文献[13]考虑高冗余的多体系统避障规划问题,采用广义势场法设计势能函数,得到避障轨迹.然而此方法计算繁琐,容易陷入局部最优解.
上述关于VGT模型的避障规划算法中均难以保证VGT各级具有大致相同的跨度,也难以防止相邻两级之间角度变化过大的问题.然而一般VGT的各级由相同材料、相同参数构成,因此运动时各级构型相似,更有利于工程实际应用.本文针对可调杆连续变化的平面VGT提出一种新的避障规划算法.首先将VGT转化为等效高冗余机械臂,分析正向运动学中冗余问题,各级给定可调杆长度后得到唯一的桁架构型.然后针对等效机械臂设计避障规划算法,得到等效模型参数,利用效模型参数还原得到VGT的各级可调杆长度.最后通过仿真验证了算法的有效性.本文采用遗传算法设计等效高冗余机械臂的避障规划问题,可以得到各级中点具有相同长度且相邻两级角度变化较小的结果.
1 问题描述
考虑平面可变形桁架系统,如图1~2所示.本文所研究的平面桁架系统由基座舱段、负载舱段及N级VGT构成,其中基座舱段和负载舱段均视为均匀密度的矩形,每一级桁架包含下方的根固定长度杆和3根可调长度杆.杆件质量集中在固定杆的左右顶点.第k级(k=1,…,N)桁架自左至右分别为可调杆rk,1、rk,2、rk,3,杆长可在范围[rmin,rmax]内连续变化,0 如图1建立系统质心坐标系XOY,原点位于系统质心O,X轴、Y轴分别与惯性系坐标轴平行;基座舱段质心坐标系XbObYb,原点位于基座质心Ob,Xb轴、Yb轴分别沿着基座舱段矩形的长边和宽边,方向如图1中所示.rb为基座舱段质心Ob到桁架的垂直距离,re为负载舱段质心Oe到桁架的垂直距离,φb为基座舱段质心坐标系角度,φe为负载舱段角度,即负载舱段长边相对系统质心坐标系X轴转过的角度,xk,f、xk,g分别为固定杆wk左、右顶点位置. s.t.rk,i∈[rmin,rmax](k=1,…,N;i= 1,2,3) 其中,bxa为桁架上任意一点的位置坐标. 本节推导桁架的正向递推运动学.考虑图2所示的VGT第k级和第k+1级桁架,k=1,2,…,N-1.已知VGT第k级固定杆的左右顶点的位置坐标为 以及第k级可调杆长度rk,i,(i=1,2,3).求取第k+1级固定杆的左右顶点位置bxk+1,f和bxk+1,g. 首先计算右顶点bxk+1,g=[xk+1,gyk+1,g]T.由图中几何关系易见 (1) 求解该方程组,当xk,f≠xk,g时 (2) 式中: 当xk,f=xk,g时,式(1)的解为 (3) 可见式(1)存在两组解(2)和(3),即由同一组可调杆杆长得到了两个可能的第k+1级右顶点.然而实际中需要避免相邻两级桁架角度变化过大,因此本文认为第k-1级桁架与第k+1级桁架分属第k级固定杆两侧.当k=1时,基座舱段与第2级桁架分属第1级桁架两侧.下面寻找(2)和(3)中满足该条件的顶点. 沿第k级固定杆,方向由左顶点指向右顶点的向量为 由第k级固定杆左顶点指向两个解点的向量分别为 两个向量分别位于wk的两侧,为判断方向,分别求下面两个叉积: 采用同样的方法计算bxk+1,f.在由rk,1,rk,2和wk+1构成的三角形中,解下面的方程组 3.1等效关节定义 基座和负载部分不变,将每级桁架转换为一组依次串联的移动关节和转动关节.如图3所示,第k级可变形桁架下端固定杆wk,上端固定杆wk+1,将wk的中心作为等效后的关节点位置xk,m.从第k个关节点依次经过移动关节qk,d和转动关节qk,θ后到达第k+1个关节点.基座舱段和负载舱段的关节点分别位于各自的质心. 参考机器人学中Danevit-Hartenberg坐标系定义方法[14],定义等效机械臂关节坐标系.如图3所示,第k组等效关节中,第k个移动关节坐标原点Ok,d位于关节起始位置中心,yk,d轴沿关节轴向,xk,d轴由右手系得出;第k个转动关节坐标原点Ok,θ位于关节中心,yk,θ轴沿着下一个移动关节qk+1,d轴向,xk,θ轴由右手系得出.在此基础上定义关节变量,移动关节的关节距离qk,d定义为原点Ok,d到Ok,θ的长度,转动关节的关节转角qk,θ定义为坐标轴xk,θ到xk+1,d的角度,逆时针为正. 3.2VGT到等效机械臂的变换关系 首先推导由VGT到等效机械臂的变换关系. 已知VGT各级桁架可调杆长度rk,i(k=1,…,N;i=1,2,3).推导等效机械臂各级关节变量qk,d、qk,θ(k=1,…,N). 由第2节可递推求得VGT各级固定点顶点在基座舱段坐标系中的坐标bxk,f、bxk,g. 由3.1节定义,可知等效机械臂关节点位置 xk,m=(xk,f+xk,g)/2 于是 (4) (5) 3.3等效机械臂到VGT的变换关系 若已知等效机械臂第k级关节变量qk,d、qk,θ,求取第k级桁架可调杆长度rk,1、rk,2、rk,3.首先由前述等效化方法及机器人建模方法,设第k个关节点的齐次坐标pk=[xk,myk,m1]T,有第k组关节的齐次变换矩阵 记基座舱段质心齐次坐标pb,负载舱段质心齐次坐标pe,则 从而得到各级关节点位置坐标xk,m.由等效机械臂转动关节角,可以得到其相对基座舱段坐标系的绝对角度 认为第k级固定杆wk的方向垂直第k+1级等效机械臂关节yk+1,d轴方向,可得顶点位置 于是可得VGT第k级可调杆长度 (6) (7) (8) 本节考虑等效模型的避障规划问题,首先由式(4)~(5)将桁架模型转化为等效模型,通过规划得到等效模型的各个中点位置后,利用式(6)~(8)可得桁架可调杆长度,由此解决桁架的避障规划问题. 考虑如图4所示的等效模型.为了优化问题方便,以及使得各级桁架具有相似的构型,本节假设各级等效模型移动关节的关节长度相同,即q1,d=q2,d=…=qN,d=qd.如图4所示,定义各级杆的相对角度为qk,θ,为第k级杆相对第k-1级杆的角度,k=1,2,…,N.q0,θ为设计参数. 下面通过求解优化问题以解决避障规划问题.优化变量为 χ=[qd,q1,θ,…,qN,θ] 求解如下的优化问题: (9) 其中do,j为第j个障碍到各个等效杆的最短距离. 求解后得到最优解χ,由上节可得各级可调杆长度rk,i,(k=1,2,…,N,i=1,2,3). 考虑可调杆连续变化的VGT,参数如下:N=21,w=1 rad,rb=0.5 m,re=0.5 m,rmin=1.2 m,rmax=1.8 m.优化问题(9)中等效杆范围为φmin=-π/6 rad,φmax=π/6 rad.障碍物个数为No=3,障碍物大小相同,ro,i=0.5 m,i=1,2,3,位置如下: 期望目标点位置为 且q0,θ=π/2 rad. 利用MATLAB的遗传算法优化求解函数ga,求解(9),得到最优解为 χ= [1.545 9 -0.443 0 -0.502 3 -0.450 9 0.049 9 0.301 1 0.238 2 -0.215 7 0.202 3 0.155 5 0.287 0 0.518 2 0.510 8 0.367 2 -0.012 0 0.409 1 0.249 3 0.188 1 0.222 8 0.399 7 0.291 5 0.040 2] (rad) 优化变量满足(9)的要求.优化目标值J=8.170 6×10-6. 仿真结果如图5~7所示.图5为优化得到的等效模型的避障规划结果.图中实心圆形区域为障碍物,共计3个.空心圆圈为等效模型的各级关节点,连接空心圆圈的实线为等效杆长,十字为期望目标点.从仿真结果可见,桁架末端与期望点几乎重合,并且各级桁架均远离障碍物.各级等效杆相对上一级杆的角度没有剧烈变化,且各级等效杆长相同,达到期望结果.图6是由等效模型计算得到桁架的避障仿真结果.从图中可见各级可调杆杆长未出现剧烈变化,且未出现跨级桁架交叉等不适合工程应用的情况,可见本文方法的有效.图7是由式(6)~(8)计算得到的该组杆长下的正向运动学.从图6和图7比较可见,两者相近.所以所提出避障规划算法有效. 考虑一类多级平面可变形桁架的避障规划问题.每一级桁架具有一个固定杆和3个可连续调长度的可调杆,多级桁架串联构成桁架系统.设计各级可调杆长度,使得末端负载达到期望点,同时各级桁架避免碰撞障碍物.针对此问题,研究了此类桁架的前向运动学,由可调杆长度得到下一级固定杆的位置坐标.并且将桁架等效成机械臂模型.通过优化方法,设计等效模型的各级杆长以及相对角度,解决等效模型的避障规划问题.由等效模型参数求得桁架可调杆参数,然后由前向运动学得到桁架各个点坐标.仿真结果验证了方法的有效性.本文的结果使得VGT等效机械臂模型各级具有相同的移动关节长度,且相邻两级转动关节角度变化较小,为工程应用提供了可行的参考. [1] MIURA K, FURUYA H, SUZUKI K. Variable geometry truss and its application to deployable truss and space crane arm[J]. Acta Astronautica, 1985, 12(85): 599-607. [2] HUANG S, NATORI M C, MIURA K. Motion control of free-floating variable geometry truss. Part 1: Kinematics[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(4): 756-763. [3] HUANG S, NATORI M C, MIURA K. Motion control of free-floating variable geometry truss. Part 2: Inverse Kinematics[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(4): 764-771. [4] MUROTSU Y, SENDA K, HISAJI K. Optimal configuration control of an intelligent truss structure[C]//Proceedings of the 1stJoint U.S./Japan Conference on Adaptive Structures. PA: Lancaster, 1991:157-175. [5] SUTTER T R, BUSH H G. A comparison of two trusses for the space station structure[C]//AIAA Structures, Structural Dynamics, and Materials Conference. Washington D.C.: AIAA, 1989. [6] UTKU S, RAMESH A V, DAS S K, et al. Control of a slow-moving space crane as an adaptive structure[J]. AIAA Journal, 1991, 25(6): 961-967. [7] HANAHARA K, TADA Y. Motion of variable geometry truss for momentum management in spacecraft[J]. AIAA Journal, 2002, 40(8): 1673-1676. [8] LATOMBE J C. Robot motion planning[M]. New York: Springer Science + Business Media, 1991. [9] NEARCHOU A C. Solving the inverse kinematics problem of redundant robots operating in complex environments via a modified genetic algorithm[J]. Mechanism and Machine Theory, 1998, 33(3): 273-292. [10] CHIRIKJIAN G S, BURDICK J W. An obstacle avoidance algorithm for hyper-redundant manipulators[C]//IEEE International Conference on Robotics and Automation. New York: IEEE, 1990. [11] MARCOS MDG, MACHADO J, AZEVEDO-PERDICOULIS TP. Trajectory planning of redundant manipulators using genetic algorithms[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(7): 2858-2869. [12] MOTAHARI A, ZOHOOR H, KORAYEM M H. A new motion planning method for discretely actuated hyper-redundant manipulators[J]. Robotica, 2017, 35: 101-118. [13] AGIRREBEITIA J, AVILÉS R, DE BUSTOS I F, et al. Inverse position problem in highly redundant multibody systems in environments with obstacles[J]. Mechanism and Machine Theory, 2003, 38(11): 1215-1235. [14] SPONG M W, VIDYASAGAR M. Robot dynamics and control[M]. New York: John Wiley & Sons, 1989. AMethodonObstacleAvoidancePlanningforVariableGeometryTruss DENG Ya, WANG Zeguo, ZHANG Jinjiang (BeijingInstituteofControlEngineering,Beijing100190,China) To design the obstacle avoidance planning method for variable geometry truss (VGT), an equivalent manipulator model is proposed. The redundant problem in the forward kinematics of single VGT is analyzed and a truss geometry is obtained with the only solution if each varied link is specified. The obstacle avoidance planning for the equivalent model is designed using genetic algorithm and optimized variables of equivalent model are obtained. Accordingly, the length of each varied link is obtained and the geometry of VGT could also be computed with the forward kinematics. In the optimized geometry of VGT, distances among middle points of fixed links remain constant and angle differences among VGT modules are small. The effectiveness of the proposed algorithm is shown via numerical simulations. variable geometry truss; obstacle avoidance; genetic algorithm; equivalent manipulator model 2017-02-18 V448.2 A 1674-1579(2017)05-0037-06 10.3969/j.issn.1674-1579.2017.05.006 邓雅(1988—),女,博士研究生,研究方向为航天器控制;王泽国(1988—),男,博士研究生,研究方向为航天器姿态控制;张锦江(1973—),男,研究员,研究方向为航天器控制、制导与仿真.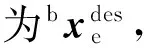
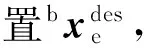
2 正向递推运动学
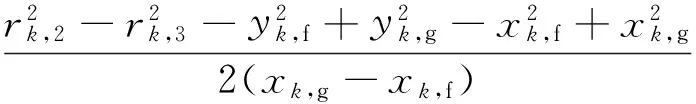
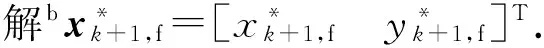
3 等效机械臂模型


4 避障规划算法
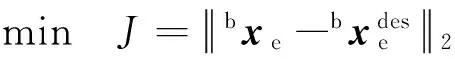
5 数值仿真
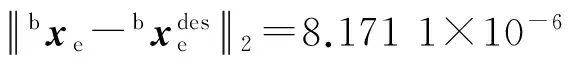
6 结 论

