基于区间算法的微小卫星微推力器阵列规模估计*
闵家麒,朱宏玉
(北京航空航天大学宇航学院,北京 100191)
*国家自然科学基金资助项目(61403031).
基于区间算法的微小卫星微推力器阵列规模估计*
闵家麒,朱宏玉
(北京航空航天大学宇航学院,北京 100191)
针对以固体微推力器阵列为执行机构的微小卫星初入轨姿态控制需求,研究固体微推力器阵列规模的估计方法.在设计了微推力器阵列单元调用规则和姿态控制律后,考虑微推力器阵列各单元冲量输出的不确定性,使用区间数表示微推力器单元的力矩输出,引入区间算法对初入轨的消旋和姿态捕获两个主要过程中微推力器单元的消耗情况进行计算.利用区间数的不相关性,改善区间计算过程,减小了由区间积分导致的区间扩张.仿真分析表明,提出的固体微推力器阵列规模估计方法可以给出预定入轨条件下的阵列规模需求,且其结果不依赖于微推力器单元力矩输出的概率特性.
姿态控制;执行机构设计;固体微推力器阵列;区间算法
0 引 言
随着微小卫星以其成本低、研制周期短、稳定灵活等优势迅速成为航天发展的热点[1],出现了多种微推进系统来完成卫星姿态调整、定位控制和轨道控制等机动任务[2].与现阶段较为成熟的冷气推进系统相比,固体微推力器阵列具有无活动部件、结构简单、系统质量轻、可批量化生产等优点[3].作为低成本卫星姿态控制的有效手段,固体微推力器阵列有进一步研究的实用价值.
目前对微推力器的研究基本集中在大规模阵列的相关技术,文献[4-5]分别研究了微推力器阵列点火电路的延迟和点火算法问题,文献[6]则着手优化了点火控制电路结构.微推力器阵列结合微小卫星姿态轨道控制的研究还较少,文献[7]基于姿轨一体化控制进行了微推力器阵列的优化利用研究,文献[8]将微推力器阵列应用到微纳卫星的编队保持控制仿真中,但上述文献均未考虑星上微推力器阵列的消耗规模问题.
实际上微小卫星空间极其有限,考虑完成任务所需星上微推力器阵列的消耗对合理利用安排星上推力器阵列规模极其重要.在微推力器阵列的安装位置偏差、微推力器装药技术等因素的影响下,直接利用动力学仿真估计星上推力器消耗存在一定不确定性.本文引入区间计算克服动力学仿真中的不确定性,并以微小卫星初入轨时的姿态控制需求为例,对微小卫星固体微推力器阵列需求规模进行了估计.
1 问题描述与设计
1.1微小卫星模型与动力学方程
本文研究自旋入轨、正常运行时三轴稳定的微小卫星初入轨控制问题,控制存在姿态消旋和姿态捕获两个控制阶段.假设星上装有陀螺和光学敏感器提供姿态角和姿态角速度测量信息,以固体微推力器阵列为控制执行机构.
记卫星质心为o,建立本体系oxbybzb,初始时卫星绕轴ozb自旋.本体系下的姿态动力学方程为
(1)
式中:I为卫星转动惯量矩阵,ω为惯性系角速度,τ为外力矩矢量.


(2)
1.2推力器阵列使用策略设计
为方便设计与修改,采用10×10小规模微正方形布局的推力器阵列作为执行机构.卫星尾部四面安装微推力器阵列,假设每面最大允许布置3×3片推力器阵列,如图1所示.d是推力器阵列推力作用点到卫星理想质心位置在推力器阵列安装平面内投影的最远距离,l是推力器阵列与卫星理想质心位置之间的最近距离.阵列间的距离为δ,阵列内推力器间距为Δd,推力器与阵列边缘的距离为Δx、Δy.
根据图1示意及坐标系定义,容易得出推力阵列所在执行机构面与能提供的控制向量的关系,见表 1.注意到,每一面推力阵列均可提供两个方向的z向力矩,且沿卫星zb轴存在对称关系.
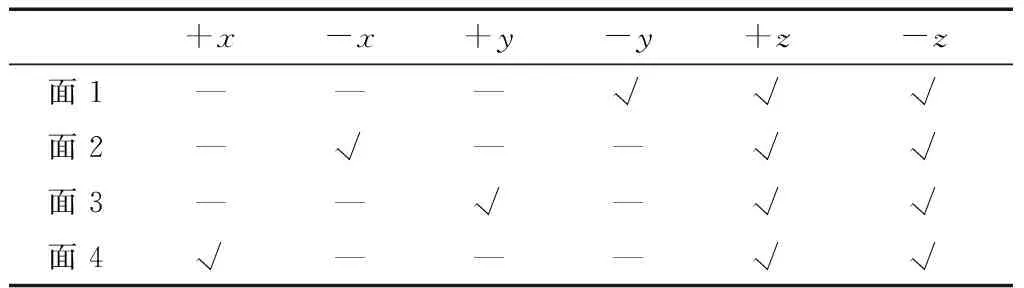
表1 执行机构所在面与控制向量对应表Tab.1 Location of the actuator corresponding to control vectors
为减小算法复杂度,推力器阵列规划采用简单的解耦法实现,即通过2个推力器组合对消的方法使每次点火组合只提供一个控制方向的冲量矩.但与文献[7]不同,本文中卫星只有四面装有推力阵列,在消除控制力矩耦合时做出限制:每一面1、3列的推力阵列提供z向力矩,而第2列阵列提供x、y向力矩.由此,以面、片(行×列)、点(行×列)的形式表示所有推力器的坐标,可得到表2中的推力器使用策略.
为了进一步减小算法复杂度,不考虑单位周期内控制力矩期望值,则对表2中各变量做出以下规定:面s=1,2,片行i从3递减到1,点行j与点行p均从10递减到1,点列k从5递减到1,点列q从1递增到10.当控制向量为x、y时,循环优先级为i高于j高于k;当控制向量为z时,循环优先级为i高于s高于q高于p.

表2 解耦法推力器使用策略Tab.2 Decoupling method for thruster application
1.3控制律设计
假设初入轨时卫星具有较大的三轴角速度和姿态角误差.为保证卫星正常工作,首先需要对卫星进行姿态消旋控制.待卫星三轴角速度稳定之后,再进行姿态捕获.
由于使用固体微推力器阵列作为控制执行机构,控制信号需要转化为开关信号[9],因此假定控制指令每隔Δt更新一次.
消旋控制使用式(3)所示的角速度反馈控制律
(3)
式中,Ti表示三轴力矩指令,Ti=0表示不需要力矩,Ti=1表示需要正向力矩,Ti=-1表示需要负向力矩;ωi_despin为预设的消旋阶段控制开关线.
考虑卫星初入轨时自旋角速度明显大于其他两轴角速度,因此消旋控制的结束判据设为
|ωz|<ωend_despin
(4)
其中,ωend_despin为消旋结束时可接受的最大自旋角速率值,可根据控制要求确定.
本文假设微小卫星正常运行时处于三轴稳定状态,因此,姿态捕获问题可以简化为向预定姿态指向的姿态机动问题.为简化控制问题,进一步假设预定姿态为零姿态,则可使用式(5)所示的反馈控制律

(5)
式中,θi为三轴欧拉角,ki为角速度反馈系数,ei为预设的姿态捕获阶段控制开关线.
与消旋结束判据类似,姿态捕获结束判据可设为
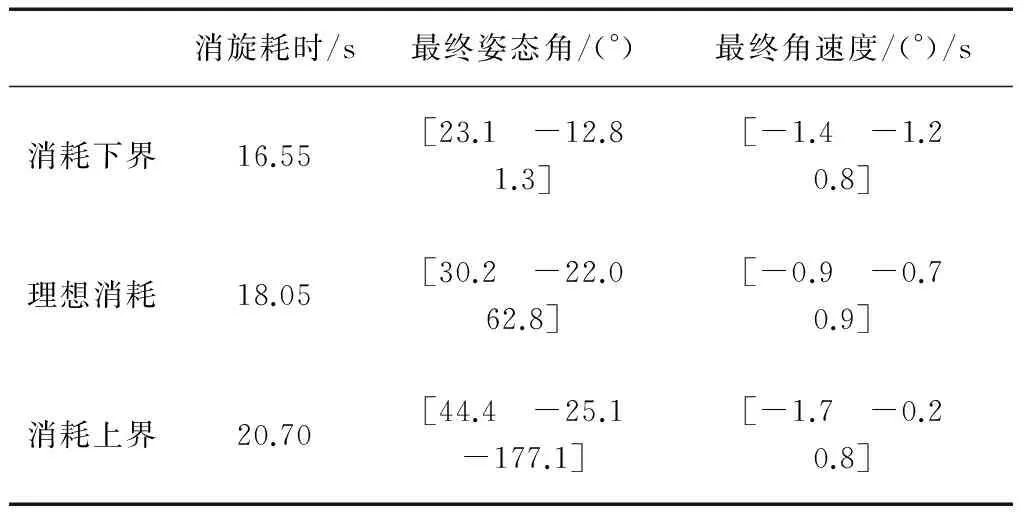
|θi| (6) 其中θi_end为卫星转入三轴稳定控制模式时所能容忍的最大姿态角. 考虑微推力器阵列的安装位置偏差、微推力器装药技术等不确定性因素影响,本文在微小卫星的动力学仿真过程中引入区间算法对微小卫星推力器消耗规模进行估计.为完成此任务,需要对仿真运算和控制律分别做出调整. 2.1区间积分的扩张抑制 (7) (8) (9) (10) (11) (12) (13) 由于卫星动力学方程式(1)、(2)的计算需要进行区间积分,这将导致严重的区间扩张现象,因此需要对问题进行简化.对式(1)的动力学方程作变形,得到角速度区间ω的计算公式 (14) (15) (16) 由于卫星的姿态角可由姿态角速度积分得到,因此可得到姿态角计算表达式: (17) 2.2控制律的区间运算调整 在引入区间算法得到卫星仿真姿态的上下界后,为了估计控制过程中微推力器消耗的上下界,需要对式(3)~式(6)的控制律作一定变形. 消旋控制阶段目的是使卫星姿态角速率迅速降为小量,因此卫星三轴角速率减小越快则消耗推力器越少.为了估计消旋控制推力器消耗,对式(3)消旋控制律中作变形: (18) (19) 姿态最终理想欧拉角为0°,因此在捕获阶段卫星姿态角变化越快则推力器消耗越少.对式(5)的姿态捕获控制律变形得到消耗下界的控制律: (20) 需要注意的是当控制律开关切换时,姿态上下界需要重置以保证控制姿态的连续.同理可得到消耗上界的控制律: (21) 考虑文献[6]中微推力器阵列研究现状,给出推力器仿真参数,见表3. 表3 推力器阵列仿真参数Tab.3 Simulation parameters of thruster array 表4为图1微小卫星模型参数. 表4 卫星模型参数Tab.4 Satellite model parameters 至此,可对卫星初入轨时姿态控制消耗需求作仿真估计. 3.1消旋控制消耗估计 表5 消旋控制阈值Tab.5 Control threshold of velocity damping (°)/s 表6消旋结果表明完成控制消耗推力器越少则控制所需时间越短,这与卫星三轴角速率减小越快则消耗推力器越少的分析相符合.另一方面,由于消旋阶段只是将三轴角速度减到小值,在不同推力器消耗情况下卫星最终姿态角可能有较大的变化,这在表6中得到了验证.因此,在消旋结束后应等待卫星姿态角缓慢转入可接受范围后再进行姿态捕获控制. 图5~7分别是仿真得到的推力器消耗下界、理想消耗和消耗上界.图中横坐标表示推力器行坐标(10×片行+点行),纵坐标表示推力器列坐标,nzi表示第i面消耗推力器数量.仿真结果证明对于消旋控制,式(16)~(17)所做假设合理,区间算法可估计推力器消耗上下界. 表6 消旋结果Tab.6 Results of velocity damping control 3.2姿态捕获消耗估计 表8中完成控制消耗推力器越少则控制所需时间越长,分析原因如下:姿态捕获阶段目的是将姿态角快速减小,单位控制周期内姿态角速率越大则姿态角减少越多,对应整个控制周期三轴角速率减小越慢则推力器消耗越少. 图11~13中推力器消耗结果表明对于姿态捕获控制,式(16)~(17)所做假设依旧合理,区间算法可估计出推力器消耗上下界. 项目数值项目数值项目数值ex2ey2ez2θx_end2°θy_end2°θz_end2°kx4ky4kz4 表8 姿态捕获结果Tab.8 Results of attitude capture 3.3仿真结果分析 由仿真验证了本文使用区间算法估计卫星初入轨姿态控制消耗推力器上下界的可行性,现对仿真结果进行具体分析. 另一方面,+z方向消耗推力器数量远大于另外两个方向.原因分析如下:1)本文研究的微小卫星自旋入轨,因此初始z轴角速度远大于x、y轴;2)表 4中推力器z向最大力臂d远小于x、y向最小力臂l,因此z向力矩远小于另两轴力矩.因此,为完成卫星消旋控制任务,在布置星上微推力器阵列时,z轴控制推力器布置应多于其余两轴. 观察图8~10的姿态曲线可以发现,推力器理想消耗的角速度曲线被消耗上下界的角速度曲线紧紧贴合,这是表10中推力器消耗上下界差值很小的原因.这表明推力器冲量矩的不确定性对姿态捕获消耗影响不大,对姿态捕获消耗推力器规模进行粗估时可直接使用理想消耗值. 表9 消旋控制各控制向量消耗推力器数量Tab.9 Thruster consumption of each control vector with damping control 表10 姿态捕获控制各控制向量消耗推力器数量Tab.10 Thruster consumption of each control vector with capture control 对比表 9与表 10中推力器消耗可知,消旋控制消耗推力器远多于姿态捕获控制消耗.因此,对微小卫星初入轨姿态控制消耗微推力器阵列规模进行分析时应重点考虑消旋控制消耗. 注意到,图14所示的微推力器最少消耗虽然能完成卫星初入轨姿态控制,但其要求清楚每一推力器单元的输出特性.因此,在实际布置星上微推力器阵列规模时可以在微推力器最少消耗的基础上留出一定余量.另一方面,若要保证微推力阵列一定能完成初入轨姿态控制,则星上微推力阵列规模应按最多消耗取. 面向微小卫星初入轨时的消旋和姿态捕获控制需求,本文使用正方形布局的固体微推力器阵列作为执行机构,完成了微推力器阵列单元调用规则和姿态控制律设计.考虑微推力器阵列各单元的冲量输出不确定性,引入区间数对初入轨控制过程中微推力器单元的消耗规模进行计算.针对卫星动力学计算过程中的区间扩张问题,本文基于区间数的不相关性对其进行了抑制,并通过仿真验证了算法的合理性. 仿真分析表明,本文提出的固体微推力器阵列规模估计方法可以给出预定入轨条件下的阵列规模需求上下界,且其结果不依赖于微推力器单元力矩输出的概率特性.按估计上界布置星上微推力器阵列一定可以完成初入轨控制要求,但实际布置星上微推力器阵列规模时更适合按估计下界加一定余量布置.对余量多少的选择,本文未进行讨论,在后续工作中可通过细分微推力器单元输出的不确定性进行研究.另一方面,估计方法可以确定微推力器单元输出不确定性对各控制环节的影响大小,利于微推力器阵列制造的成本控制. [1] 林来兴, 张小琳. 迎接“轨道革命”——微小卫星的飞速发展[J]. 航天器工程, 2016,25(2):97-105. LIN L X, ZHANG X L. Meeting the “track revolution”—the rapid development of micro satellites[J]. Spacecraft Engineering, 2016,25(2):97-105. [2] 林来兴. 现代小卫星的微推进系统[J]. 航天器工程,2010,19(6): 13-20. LIN L X. Micro-propulsion system for modern small satellite[J]. Spacecraft Engineering, 2010,19(6):13-20. [3] 刘建忠, 梁导伦, 汪洋,等. 基于MEMS的固体燃料微推进技术研究进展[J]. 纳米技术与精密工程, 2016,14(1):48-54. LIU J Z, LIANG D L, WANG Y, et al. Review on MEMS-based solid propellant micro-propulsion[J]. Nanotechnology and Precision Engineering, 2016,14(1):48-54. [4] 刘旭辉, 方蜀州, 王玉林,等. 大规模固体微推力器阵列点火关键技术[J]. 固体火箭技术, 2012,35(2):183-187. LIU S H, FANG S Z, WANG Y L, et al. Ignition key technology of large-scale solid micro-thruster array[J]. Journal of Solid Rocket Technology, 2012,35(2):183-187. [5] 刘旭辉, 方蜀州, 刘书杰,等. 微型姿控固体推力器阵列点火算法[J]. 航空动力学报, 2011,26(7):1659-1664. LIU X H, FANG S Z, LIU S J, et al. Ignition algorithm of solid propeller micro-thruster array for attitude control[J]. Journal of Aerospace Power, 2011,26(7):1659-1664. [6] 汝承博, 许建兵, 代骥,等. 基于MEMS的固体化学微推进器阵列技术综述[J]. 爆破器材,2016,45(6):1-10. RU C B, XU J B, DAI J, et al. Study of MEMS-based solid chemical micro-thruster array technology[J]. Explosive Materials, 2016,45(6):1-10. [7] 刘旭辉, 方蜀州, 马红鹏, 等. 基于固体微推力器阵列的卫星控制一体化算法[J]. 固体火箭技术, 2012,35(1):17-23. LIU S H, FANG S Z, MA H P, et al. Integrated control algorithm based on solid propellant micro-thruster array[J]. Journal of Solid Rocket Technology, 2012,35(1):17-23. [8] 范林东, 杨博, 苗峻, 等. 基于SiC MEMS阵列的高精度微纳卫星编队保持[J]. 中国空间科学技术, 2016,V36(2):37-45. FAN L D, YANG B, MIAO J, et al. High precision micro-nano satellite formation keeping based on SiC MEMS micro thruster array[J]. Chinese Space Science and Technology, 2016,V36(2):37-45. [9] HAO D, SHENG T, CHEN X. Small satellite magnetism control for velocity damping[C]//Second International Conference on Digital Manufacturing & Automation. IEEE Computer Society. New York: IEEE, 2011. [10] MOORE R E, KEARFOTT R B, CLOUD M J. Introduction to Interval analysis[M]. Society for Industrial and Applied Mathematics, 2009. EstimationofMicro-ThrusterArrayConsumptionforMicro-SatelliteBasedonIntervalAlgorithm MIN Jiaqi, ZHU Hongyu (SchoolofAstronautics,BeihangUniversity,Beijing100191,China) A method for solid propellant micro-thruster array consumption estimation is proposed in this paper for attitude control of micro-satellite in orbit entry stage. The micro-thruster unit call rule and attitude control laws of velocity damping and attitude capture are designed. Considering the uncertainty of each micro-thruster unit impulse output, we use the interval number to represent the micro-thruster unit torque output and then estimate the consumption of the micro-thruster unit for attitude control with interval algorithm. By means of the irrelevance of interval number, the interval computation process is improved, and the interval expansion induced by the interval integral is reduced. Numerical simulations demonstrate that the estimation method is not dependent on the probability characteristic of the micro-thruster unit torque output. attitude control; actuator design; solid propellant micro-thruster array; interval algorithm 2017-04-09 V448.22 A 1674-1579(2017)05-0022-09 10.3969/j.issn.1674-1579.2017.05.004 闵家麒(1993—),男,硕士研究生,研究方向为卫星姿态控制;朱宏玉(1976—),男,讲师,研究方向为航天器动力学与控制.2 固体微推力器阵列需求规模估计方法
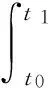
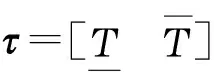

3 算例仿真





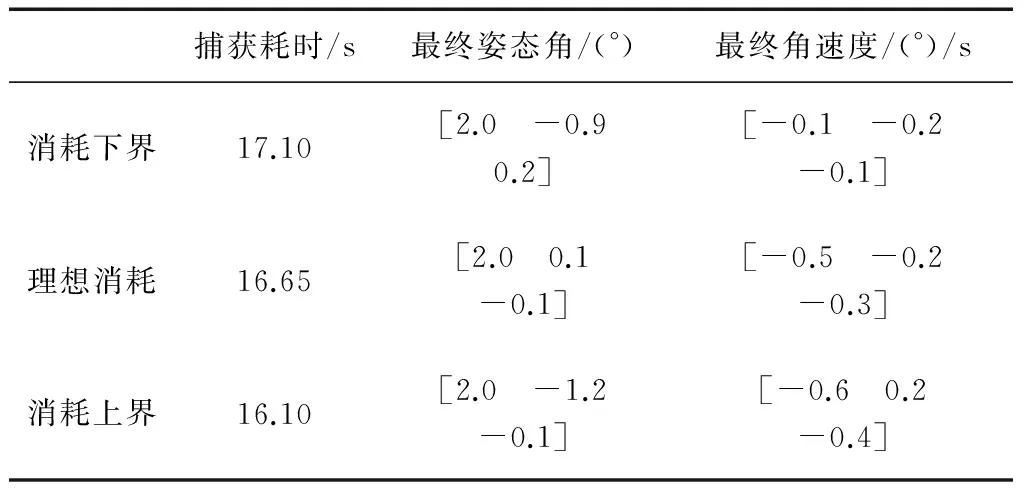


4 结 论

