九自由度运动模拟器相对位置精度分析与指标分解*

李 博，吴奋陟，王云峰，何华东，付铜玲，许 波

(1.天津市微低重力环境模拟技术重点实验室，天津 300458； 2.天津航天机电设备研究所，天津 300458； 3. 北京控制工程研究所，北京 100094)

*天津市科技支撑计划(14RCHZGX00874)和国家青年科学基金(51505331).

九自由度运动模拟器相对位置精度分析与指标分解*

李 博1,2，吴奋陟3，王云峰1,2，何华东1,2，付铜玲1,2，许 波1,2

(1.天津市微低重力环境模拟技术重点实验室，天津 300458； 2.天津航天机电设备研究所，天津 300458； 3. 北京控制工程研究所，北京 100094)

九自由度运动模拟器是标定航天器交会对接GNC子系统中交会对接光学成像敏感器(CRDS)的关键设备，具有较高的相对位置精度要求.以此为出发点，对影响系统综合指标的误差组成进行系统性分析.梳理各误差分量的关系及相互作用原理，建立误差模型，通过对系统综合指标进行合理的分解与分配，最终使九自由度运动模拟器系统精度达到设计要求.

九自由度； 运动模拟器；相对位置精度；误差分析；指标分解

0 引 言

交会对接光学成像敏感器(CRDS)，由安装于追踪飞行器上的相机和目标飞行器上的目标标志器共同组成，其性能是交会对接成功与否的关键[1-2].通常情况下，CRDS的地面标定和验证由九自由度运动模拟器予以实现，因此，九自由度运动模拟器是航天器交会对接的地面关键支撑设备之一.

“6+3”式九自由度运动模拟器主要用于交会对接GNC子系统级的试验验证[3]，对模拟器相对位置精度的要求不高.本文所述九自由度运动模拟器为CRDS的产品级标定设备，因而对系统精度提出了更高的要求——全行程综合位置误差优于0.5 mm，同时考虑成本和研制周期的影响，传统“6+3”式运动模拟器难以满足项目需求，故而采取全新的“5+4”式自由度分配形式.

参照前人的研制经验，全行程综合位置误差的影响因素主要包括直线度、不相交度、不垂直度以及直线与回转的定位精度.因此，建立系统综合位置误差与各个分项误差的数学模型，分析后者对前者的影响，并兼顾工程可实现性，进行各个分项误差的指标分解，是项目实施的重要依据，同时具有重要的意义.

本文首先对影响系统综合位置精度的误差分量进行辨识；其次借鉴尺寸链的计算方法，建立组成环误差与封闭环误差的关联模型；再者依据应达到的封闭环误差计算各组成环应满足的误差精度；最后，采用迭代的方法实现相对位置精度的指标分解.

1 模拟器简介

九自由度运动模拟器如图1所示，包含两大机械分系统：高精度转台分系统(追踪转台、目标转台)、直线运动分系统(x向运动分系统、y向运动分系统、z向运动分系统).其中，两转台均为三轴转台，由外而内依次为偏航轴、俯仰轴和滚动轴，初始状态时偏航轴为竖直轴，俯仰轴、滚动轴为水平轴.

2 影响因素分析

鉴于九自由度运动模拟器相对位置误差的影响因素较多，若采用整体的分析方法，会导致计算过程繁琐，不利于突出主要影响因素，甚至使得分析无法进行[4-5].因此，需将影响因素拆分为转台转动位置误差源和直线系统位置误差源，拆分后分别进行运算，将得到的结果再进行叠加得到整体相对位置误差[6-7].

表1 影响相对位置精度的误差分项识别Tab.1 Identify of error constituents affecting relative position precision

3 综合位置指标影响分析

3.1转台不相交度

为分析转台不相交度对两模拟器相对位置误差的影响，按图2所展示的流程进行分析，考虑转台的三轴不相交度的误差来源，建立图3所示的数学模型[8].其中r为负载盘距三轴中心距离.

在一般状态下rOM相对o0-x0y0z0坐标系的矢量坐标为

(1)

考虑不相交度影响的rOM′相对o0-x0y0z0坐标系的矢量坐标为

(2)

位置误差rMM′相对o0-x0y0z0坐标系的矢量坐标为

(3)

由于偏航角φ1与俯仰角φ2是相对独立的两个量，φ1∈(-50°,50°)，φ2∈(-32.5°,32.5°)，不相交度Δ∈(0,0.35)，因此rMM′各分量的最大值(不同时为最大值)通过代入得到三向分量分别为：

i=(±Δsinφ1sinφ2±Δcosφ1)max=0.369

(4)

j=(±Δcosφ2)max=0.35

(5)

k=(±Δcosφ1sinφ2±Δsinφ1)max=0.389

(6)

通过以上计算可以看出三向分量数值较为显著，但是转台不相交度是一项稳态误差，经过加工装配之后，各不相交度值均已确定，并可通过相应手段检测出来，为最有效避免不相交度引入的位置误差，可利用测量结果，将其设置成为理论模型中的一部分，最终通过运动控制进行相应位置补偿.

3.2转台不垂直度

为分析转台不垂直度对两模拟器相对位置误差的影响，按图4所展示的流程进行分析，考虑转台的三轴不垂直度的误差来源.

基本假设[9]：

1)转台三个轴线不垂直，但三轴线相交与一点；

2)转台不垂直度只发生在相邻两轴线之间，比如偏航轴(轴Ⅲ)与俯仰轴(轴Ⅱ)、俯仰轴(轴Ⅱ)与滚动轴(轴Ⅰ)，而偏航轴与回转轴之间无此概念；

3)轴Ⅰ与轴Ⅱ的不垂直度角ε应在轴Ⅱ与Z轴两相交线所构成的平面内部，如图5(a)所示，为了方便计算，且轴Ⅱ-Z轴平面与XOZ平面夹角极小，可近似看做在XOY平面内，轴Ⅲ与X轴夹角为ε，如图5(b)所示.

在笛卡尔坐标系中建立半径为r(r为负载盘中心距三轴焦点的距离，按照设计取640 mm)的球体，将转台的3个轴线融入到此球体之中，转台的三轴相交于一点，将此点放置在球心O处，轴Ⅲ与Y轴重合，轴Ⅱ在YOZ平面内，由于不垂直度因素的存在轴Ⅱ与Y轴有夹角ε；轴Ⅰ在XOZ平面内，由于不垂直度因素的存在轴Ⅰ与Z轴有夹角ε，状态如图6(a)所示.

N′点在球面上：

(7)

EN′与轴Ⅱ垂直：

x0+y0ε-(z0-r)ε=0

(8)

OE与ON′夹角：

cosθ=z0/r

(9)

另有点F(0,-2εr,r)在弧线上，通过以上条件的联立，能够得到N′点以θ为参数关系的坐标点

x0=(1-cosθ+sinθ)εr

(10)

y0=rsinθ

(11)

z0=rcosθ

(12)

在考虑转台不垂直度模型时，转台经过调节与标定达到理想位置后，仅轴Ⅱ的回转产生X向误差分量，在转动最大角行程32.5°时，通过式(10)可以得到，X向误差大小为0.006 mm.

此偏差主要由于滚动轴承的偏心量引起，虽然有一定的周期性，但其不属于稳态误差，不能进行补偿.

3.3三向直线运动

为分析直线系统误差对两模拟器相对位置误差的影响，按图7所展示的流程进行分析.

建立九自由度运动模拟器空间模型(不含三轴转台部分)，如图8所示，在Z向与X向导轨交点处建立坐标系，基准坐标系Z轴与Z向导轨拟合直线重合基准坐标系X轴在水平面上且与Z轴正交，Y向由右手法则确定.

影响目标器位置精度的主要因素有[10]：

θ1为在运动方向上由于Z向导轨的水平度变动对目标器产生的俯仰角(rad)(图9)；

θ2为由于Z向双导轨的高度偏差，对目标器模拟器产生的侧倾角(rad)(图10)；

△z为目标器Z向位置控制误差(mm)(图11)；

图9 导轨直线度导致的俯仰角变化
Fig.9 Pitching angle error due to nonlinearity of the rail

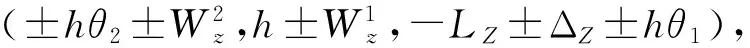
(13)

影响追踪器位置精度的主要因素有：

α为X向导轨与Z向导轨的不垂直度(rad)；

θ3为在运动方向上由于X向导轨的水平度变动对目标器产生的俯仰角(rad)；

θ4为由于X向双导轨的高度偏差，对目标器模拟器产生的侧倾角(rad)；

Δx为目标器X向位置控制误差(mm)；

Δy为目标器Y向位置控制误差(mm)；

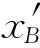
(14)

(15)

(16)

则rBB′向量表达式为：

(17)

相对位置误差应为追踪器与目标器实际位置矢量rA′B′与理论位置矢量rAB之差，由于rA′B′+rB′B+rBA+rAA′=0，则有

rA′B′-rAB=rA′A-rB′B

(18)

计算得到：

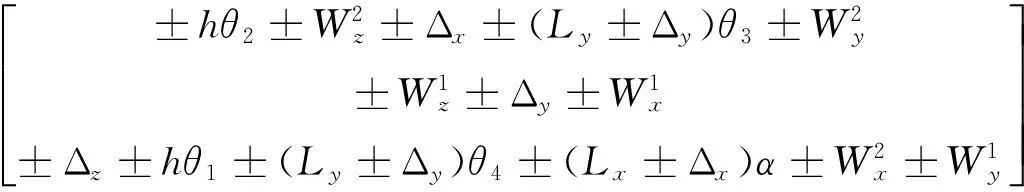
(19)

展开各式，将所有误差同向累加，并去除对系统误差影响不大的二阶小量，得到最大相对位置误差的X向分量为

(20)

最大相对位置误差的Y向分量为

(21)

最大相对位置误差的Z向分量为

(22)

用概率法计算各组成环的叠加量，将式(20)～(22)分别转换为式(23)～(25):

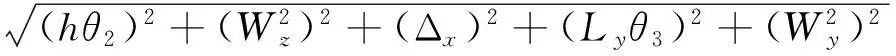
(23)

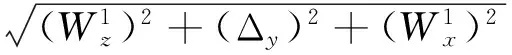
(24)

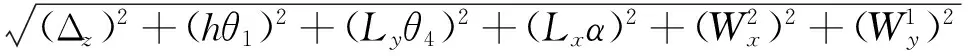
(25)

将直线系统各分量误差分量的初始值(任务中要求值)代入到上述尺寸链中会发现不能满足要求，需要迭代运算直至相对位置误差到要求值的60%左右，并在此过程中考虑工程可实施性，最终形成影响综合指标的各组成分项指标的叠加分量，见

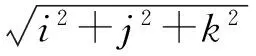
表2 全行程系统相对位置偏差Tab.2 Relative position errors /mm

3.4指标分解

通过初始值代入尺寸链中进行计算得到初始的综合位置误差，与预计的指标要求有一定的偏差，因此需要再次修正各分项误差指标，经过几轮反复计算后得到合适的分项误差，将最后一次迭代的分项误差结果做疏理统计与初始值进行对比，形成表3，表中同时把工程实现值的数据进行了梳理与比对，能够看出严格以分解指标为依据对项目进行执行和把控.

表3 直线系统各分量误差分量的初始值与确认值Tab.3 Initial values and validated values of linear system error components

4 结 论

本文建立转台系统不相交度、不垂直度以及直线系统误差模型，分析各类误差的作用形式及处理方法，通过尺寸链的概率计算能够得到较为经济的各分项误差值，且整个分配过程严格考虑了各个系统的实现性，避免了无法工程实现的问题.此项目的执行过程严格依照本文的结果把控，目前对目标器45个位置和追踪器34个位置点位进行测量，共1 530个排列结果，综合位置精度均满足0.5 mm要求.本指标分析与分解方法有较为普遍的适应性，对其他复杂高精度机械系统的指标实现性分析有参照价值.

[1] 龚德铸，赵春晖，张琳，等.交会对接光学成像敏感器的LD照明系统[J]. 空间控制技术与应用，2014，40(5)：57-62.

GONG D Z， ZHAO C H， ZHANG L， et al. LD lighting system for camera-type rendezvous and docking sensor[J]. Aerospace Control and Application， 2014,40(5):57-62.

[2] 刘勇，孙玉平，强博文. 高精度工业测量模拟器交会动态测试技术研究[J]. 测绘与空间地理信息, 2014,37(7):47-49.

LIU Y， SUN Y P， QIANG B W. Research on the technologies of dynamic test of movement simulator with high-precision industrial measurement[J]. Geomatics & Spatial Information Technology, 2014,37(7):47-49.

[3] 张新邦，刘良栋，刘慎钊. 航天器交会仿真试验的运动模拟器[J]. 空间控制技术与应用，2009,35(2):51-55.

ZHANG X B，LIU L D，LIU S Z. Motion simulators for rendezvous simulation test[J]. Aerospace Control and Application，2009,35(2):51-55.

[4] 郑兴林，马龙. 空间环境下的三维运动模拟器设计与应用研究[J]. 航天器环境工程, 2009, 26(5):442-446.

ZHENG X L， MA L. Design and application of three-dimensional movement simulator under space environment[J]. Spacecraft Environment Engineering, 2009, 26(5):442-446.

[5] 寇江伟.空间交会对接运动模拟器误差模型的研究[D].哈尔滨：哈尔滨工业大学, 2005.

KOU J W. The Error model research of spacecraft docking motion simulator[D]. Harbin: Harbin Institute of Technology, 2005.

[6] 刘义乍，章苛，赵小松，张志飞．数控机床全误差模型和误差补偿技术的研究[J]．制造技术与机床，2003(7)：46-51.

LIU Y Z，ZHANG K，ZHAO X S，ZHANG Z F. Research on total error model and error compensation of CNC machine tool[J]. Manufacturing Technology & Machine Tool, 2003(7):46-51.

[7] 石则昌，刘深厚．机构精确度[M]．北京：高等教育出版社, 1995.

[8] 粱凯,苏建刚,邱铭铭. 六自由度运动模拟器性能指标分析[J]. 电光与控制, 2008,15(6):83-87.

HANG K，SU J G，QIU M M. Analysis on performance indexes of a six-degree-of-freedom motion simulator[J]. Electronics Optics & Control, 2008,15(6):83-87.

[9] 田浩, 赵阳, 张大伟. 对接机构综合试验台运动模拟器建模分析[J]. 宇航学报, 2007,28(4):997-1001.

TIAN H，ZHAO Y，ZHANG D W. Movement simulator modeling and simulation in integrate test platform for docking mechanism[J]. Journal of Astronautics, 2007,28(4):997-1001.

[10] 审志刚，谌永祥．三坐标数控机床误差补偿技术研究[J]．机床电器, 2004(1):22-24.

SHEN Z G， CHEN Y X. Technical research of the error compensation of three coordinates CNC machine tool[J]. Machine Tool Electric Apparatus, 2004(1):22-24.

RelativePositionPrecisionAnalysisandDecompositionof9DegreeofFreedomMotionSimulator

LI Bo1,2, WU Fenzhi3, WANG Yunfeng1,2, HE Huadong1,2, FU Tongling1,2, XU Bo1,2

(1.TianjinKeyLaboratoryofMicrogravityEnvironmentSimulationTechnology,Tianjin300458,China; 2.TianjinInstituteofAerospaceMechanicalandElectricalEquipment,Tianjin300458,China; 3.BeijingInstituteofControlEngineering,Beijing100094,China)

9 degree of freedom motion simulator (9-DOF-MS) is the key equipment for calibration of camera-type rendezvous & docking sensor (CRDS) in spacecraft rendezvous and docking guidance navigation and control (GNC) sub-system, and it must be with high relative position precision. To meet this demand, the components of errors impacting this system’s integral indexes are analyzed systemically in this paper. At first, the relationship and interactions among the components of system errors are analyzed. Then the error model is built. By decomposing and redistributing the systematic precision index, 9-DOF-MS design fulfills the precision requirements.

9 degree of freedom；motion simulator；relative position precision；error analysis; index decomposition

2017-05-06

V416.8;V448.25+3

A

1674-1579(2017)05-0049-06

10.3969/j.issn.1674-1579.2017.05.008

李博(1987—)，男，工程师，研究方向为机械系统设计与分析；吴奋陟(1986—)，女，工程师，研究方向为空间视觉测量敏感器测试技术；王云峰(1983—)，男，工程师，研究方向为结构动力学与振动控制；何华东(1987—)，男，工程师，研究方向为机械设计与测量；付铜玲(1985—)，女，工程师，研究方向为微低重力模拟与仿真；许波(1985—)，男，工程师，研究方向机械系统设计与分析.