考虑控制约束和不确定性的火星最优进入制导

李毛毛

(北京控制工程研究所，北京 100190)

考虑控制约束和不确定性的火星最优进入制导

李毛毛

(北京控制工程研究所，北京 100190)

针对火星进入段控制受约束、大气环境以及探测器自身参数不确定性等问题，提出控制受约束的火星最优鲁棒进入制导方法.将针对参数不确定系统的最优性能指标转换为针对标称系统的修正性能指标；同时考虑控制约束，在性能指标中引入饱和函数，将制导问题转化为求解修正Hamilton-Jacobi-Bellman (HJB)方程问题；由于HJB方程是偏微分方程，求解有难度，利用神经网络的逼近能力近似求解.本文制导方法保证了不确定系统有最优的性能指标上界和较强的鲁棒性.最后将其应用到火星进入制导中，仿真结果表明系统存在不确定的情况下，仍可以很好地满足火星进入段终端条件，控制量也在约束的范围内，从而验证所提方法的有效性.

不确定系统；控制约束；HJB方程；火星进入制导

0 引 言

大气进入制导是航天器成功着陆星球，进行各项科学研究和实验的前提.航天器返回地球技术研究较深入.作为距离地球最近的行星之一，火星在很多方面都与地球相似，已经成为人类进行深空探测的重要目标天体[1].航天器进入火星的过程分为进入段(entering)、下降段(descent)和着陆段(landing).由于火星大气层非常稀薄，整个进入过程时间短，状态变化快，对减速性能的要求也很高.火星大气具有很大的不确定性，时常出现狂风，沙尘等天气，因此具备一定自适应能力的制导方法，已经成为了国内外火星领域的研究热点[2-3].最初，设计目标主要考虑在进入段终端，航天器速度和高度尽可能满足要求[4].目前，成功着陆火星的探测器，在进入段，早期的探测器采用无升力弹道式进入，最新的火星科学实验室(MSL)和海盗号采用弹道升力式进入.弹道升力式因为着陆精度高，必将成为趋势.近年来，随着对火星探测需求的改变，着陆点的环境却更加恶劣，需要实现火星探测器精确着陆[5-6].

火星大气进入过程分为跟踪标称轨道的制导方法和预测校正的制导方法，具体细分为标准轨道法、解析预测校正算法、能量控制算法和数值预测校正算法等[7-8]，这些算法均以改变倾侧角的大小和幅值来控制进入段的轨迹.针对跟踪标称轨道的制导方法，有学者利用线性轨迹跟踪律实现6个参考轨迹状态的跟踪，并提出实时计算跟踪律增益的理论[9].但是由于火星大气进入系统的强非线性和时变特性，使用LQR方法会引起较大的跟踪误差.采用滑模变结构控制可获得较好的制导精度，但由于抖振的存在使其难以用于工程.Benito和Mease[10]利用非线性模型预测控制可以实现很高的制导精度，但是较大的计算负担限制了该方法在实际中的应用.Restrepo和Valasek[11]利用直接模型参考自适应控制有效克服参数不确定的影响，使系统获得较强的鲁棒性.由于火星进入段的系统方程是高度非线性和时变的，利用线性系统的理论设计制导律，会导致制导精度不够.近年来，非线性最优控制问题引起了学者的广泛关注,以上方法，都没有考虑火星进入制导中非线性最优制导与控制问题，这是本文需要解决的问题.

本文针对火星进入段的制导问题，利用最优控制思想去跟踪标称轨迹，保证系统有一个最优的性能指标.对非线性系统设计最优控制律，需要求解HJB方程，其为非线性的偏微分方程无法得到解析解.目前，国内外学者提出了多种近似求解HJB方程的方法.Beard[12]针对有限时间和无限时间域的非线性最优控制问题，提出了一种Galerkin近似方法求解HJB方程.Cheng等[13-14]提出了利用神经网络，无需策略迭代可近似求解有限时间域的非线性最优控制问题，同时指出基于神经网络逼近能求出时不变和时变HJB方程的近似解，充分利用神经网络的万能逼近能力，将求解HJB方程问题转化为求神经网络权值问题，较于其他方法，运算量少，工程实现也更容易.

在火星进入段的过程中, 火星探测器的质量和气动系数会存在不确定性，纵向制导控制量很容易超出界限，在本文中，考虑控制量受约束的非线性不确定系统的最优鲁棒制导律.

1 火星进入制导问题

1.1火星进入段模型

火星进入段制导分为纵向和横向制导，纵向通过改变倾斜角的幅值来进行控制，而横向改变倾斜角的符号来进行控制，利用倾斜角换向逻辑来实现纵横向控制的解耦.一旦横程误差超过规定阈值，倾斜角的符号就反号.本文中，主要考虑纵向制导问题，进入段制导中状态量：高度，速度和飞行路径角是定义在纵向平面内的，和横向状态是解耦的，所以考虑进入段纵向制导采用如下的状态方程[11]：

(1)

(2)

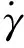
(3)

(4)

式中：r为航天器到火星球体中心的距离；v为航天器相对火星的速度；γ为飞行路径角；s为航天器航程；σ为倾斜角；L为火星探测器升力加速度，L=0.5ρv2CLS/m；D为火星探测器阻力加速度，D=0.5ρv2CDS/m；gm为火星重力加速度；ρ为火星大气密度，ρ=ρrexp[-(r-r0)/hs].

1.2火星进入段跟踪模型的建立

火星进入段采用的是基于参考轨迹的标准轨迹制导方法，本文中采用高斯伪谱法规划标称轨迹.

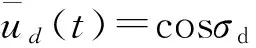
(5)

(6)

(7)

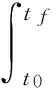
针对误差系统(7)，结合非线性系统的最优控制思想，希望寻求u(t)如下性能指标最小：

V(x(t0),t0)=l(x(tf),tf)+

(8)

2 考虑控制约束和不确定性的最优鲁棒控制

2.1基本定义和定理

考虑含有不确定性的仿射连续非线性系统[15]

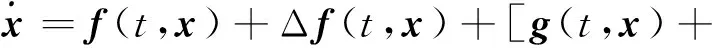
(9)

式中，x(t)∈Rn是状态量，u(t)∈Rm是控制输入，f:R×Rn→Rn,Δf:R×Rn→Rn和g:R×Rn→Rn×mΔg:R×Rn→Rn×m是分段连续的并且在[t0,tf]×Ω局部李普希兹连续的，Ω是一个闭集.本文中只考虑Δg=0的情况，Δf(t,x)表示带有不确定项的系统对标称系统的非线性不确定干扰项，定义Ρ[t0tf]×Ω.标称系统如下式所示：

(10)

定义1.在反馈控制作用下，定义φ(τ;t0,x0,u)为闭环系统在初始状态(t0,x0)和控制量u(t)=φ(t,x)作用下，系统在τ时刻的解.

考虑提出有限时间域内的性能指标：

JF(t0,x0,φ)=s(φ(tf))+

(11)

其中，s:Ω⊂Rn→R是单调递增的正定函数,s(φ(tf))表示对终端状态误差的惩罚.上面的性能指标需要考虑到控制量φ(t)是有界的，假设φ(t,x)被饱和函数ψ(·)约束(比如tanh等)，定义积分形式的函数[14]如下：

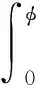
式中，ψ-T(v)=[θ-1(v1),θ-1(v2),…θ-1(vm)],v∈Rm，ψ∈Rm是有界的一对一函数，而且它的倒数也是有界的.W(φ)标量，R是正定矩阵.

在求解最优控制问题时，给出容许控制的概念，确保性能指标(11)是有限的.

定义3.对于标称系统(10)，如果满足下面的3个条件：

(1)φ(t,x)在Ρ内是连续可微的；

(2)φ(t,x)在Ρ内有有界响应；

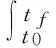
那么称控制律u(t)=φ(t,x)是容许控制.

对于不确定系统(9)，若控制律u(t)=φ(t,x)对于所有的容许不确定项Δf∈F时，都是容许控制，则有控制律u(t)=φ(t,x)对不确定系统来说是鲁棒容许控制，记为u(t)=φ(t,x)∈RA(Ρ).

有限时间最优鲁棒控制问题就是找到u(t)=φ(t,x)∈RA(Ρ)，使针对不确定系统的性能指标上边界Jb<+∞，并且使这个上界越小越好，则控制律在时间间隔[t0,tf]就有一个鲁棒有界响应，并且使性能指标满足JF(t0,x0,φ)≤Jb.

定理1.考虑不确定系统(9)在控制u(t)=φ(t,x)作用下，提出的性能指标形式为式(11).假设存在函数V:Ρ→R, Γ:Ρ→R和φ∈RA(Ρ)，V是一个连续可微函数，满足

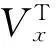
(12)

式中，下标x和t表示针对状态量和时间的偏微分，那么控制律u(t)=φ(t,x)在时间区域[t0,tf]有一个鲁棒有界响应，并且代价函数满足

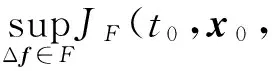
(13)

式中：

J(t0,x0,φ)(φT(t)Qφ(t)+W(φ)+ Γ(t,φ(t)))dt+s(φ(tf))

(14)

φ(t)表示标称系统(10)的解.

Δf(t,x)满足如下形式[15]：

F{Δf:P→Rn:Δf(t,x)=Gδ(t,x)δ(hδ(t,x)),

t∈[t0,tf],x∈Ω,δ(·)∈Δ}

式中，Δ={δ:Rpδ→Rmδ,δT(y)δ(y)≤mT(y)m(y),δ(0)=0,y∈Rpδ}，Gδ:Ρ→Rn×mδ,hδ:Ρ→Rpδ,δ:Rpδ→Rmδ是一个不确定的函数，m:Rpδ→Rmδ是一个给定的函数.

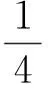
ξ>0是引出的一个参数.

证明.利用参考文献[16]中引理3.2.4，易得类似结论，当且仅当u(t)=φ(t,x)在区域Ρ内有鲁棒有界响应，有u(t)=φ(t,x)∈RA(Ρ).因为u(t)=φ(t,x)∈RA(Ρ),易得控制律u(t)=φ(t,x)在时间区域t∈[t0,tf]有一个鲁棒有界响应.

由式(12)可得

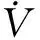
在有限时间间隔内积分，易知对于所有的容许不确定Δf∈F，

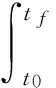
因此：

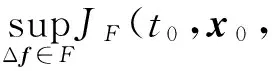
又

=-(φT(t)Qφ(t)+W(φ)+Γ(t,φ(t)))

积分可得

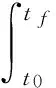
及J(t0,x0,φ)=V(t0,x0)，φ(t)及φ(t;t0,x0,φ)表示针对标称系统的解.

定理1证明完成.

2.2神经网络求解控制约束的最优鲁棒问题

结合定理1，针对标称系统，定义修正的指标函数

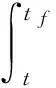
(15)

H(t,x,φ,Vx)=φT(t)Qφ(t)+W(φ)+

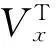
(16)

存在一个最优控制φ*，并且φ*满足标称系统的容许控制的定义，最优指标函数V*解析式为

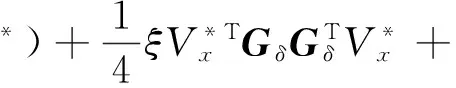
(17)

最优控制：

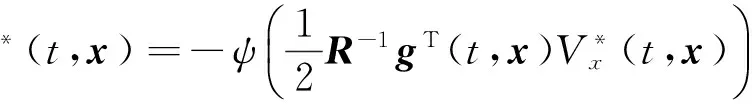
(18)

将式(18)代入式(17)中，可得修正的HJB方程：

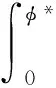
(19)

可以看出，最优鲁棒控制问题的解需要依赖于求解修正的HJB方程(19)，只要得到V*(t,x)，就可以由式(18)求得最优鲁棒控制.但是HJB方程是非线性偏微分方程，很难求解，如引言所述，利用神经网络可以近似的逼近函数V*(t,x)，从而求解HJB方程.利用神经网络VL(t,x)在区域Ρ内近似逼近V*(t,x).

(20)

式中，σL(x)=[σ1(x) …σL(x)]T是神经网络的激活函数，wL(t)=[w1(t) …wL(t)]T是时变的神经网络输入层权值.L是神经网络隐含层的个数，隐含层到输出层的权值为1.

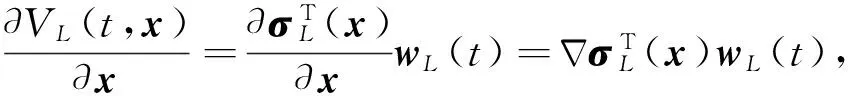
由此，用神经网络逼近求解修正的HJB方程为

(21)

最优鲁棒控制量为

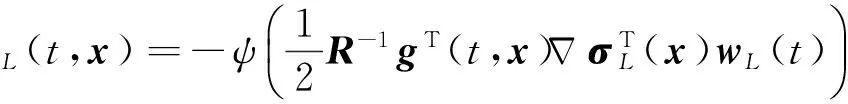
(22)

由于神经网络是近似的逼近，存在残差

ξL(t,x)=HJB(VL(t,x))

(23)

(24)

利用文献[14]中加权残差法的思想，可以得到权值的最小二乘解，加权残差法有

〈σL(x),ξL(t,x)〉Ω=0

(25)

则有：

(26)

注1.利用神经网络近似逼近函数V*(t,x)，则存在HJB方程，神经网络权值，近似函数以及最优鲁棒控制量收敛性证明.利用文献[16]引理5.2.14、推论5.2.16、引理5.2.17，可以类似的证明，随着神经网络隐含层个数的增加，HJB方程，神经网络权值，近似函数以及最优鲁棒控制量的收敛性可以得到保证.

3 仿真校验

为了验证第2节所提方法的有效性，在给出仿真参数后，用高斯伪谱法得到标称轨迹，然后利用最优鲁棒控制方法进行标称轨迹的跟踪.在系统中考虑不确定性，本文中

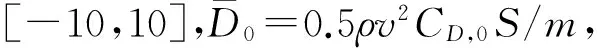
考虑控制约束，输入惩罚函数为

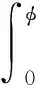
(27)

输入约束为|φ(t)|≤A=0.97.

神经网络的形式如下：

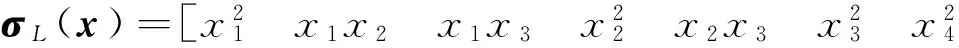
仿真中，进入段初始状态为：初始高度126 km，初始速度6 000 m/s,初始飞行路径角-15.2°.针对多种正负初始误差的组合，进行了仿真校验，初始误差范围如下：初始高度误差范围[-1 500,1 500] m；初始速度误差范围[-150,150] (m/s)；初始飞行路径角误差范围[-0.1,0.1] (°)；初始航程误差范围[-12 000,12 000] m.由图1～4可以看出即使系统存在不确定性，跟踪误差亦有很好的抑制效果.在进入段终端，高度误差范围在200 m以内，速度误差在15 m/s内，飞行路径角误差在0.01°内，航程误差在2.5 km内，满足了终端误差的要求.

本文考虑了控制约束的情况，由图5可知，不管初始误差多大，经过多次仿真，倾斜角的余弦值都在0.97的范围内，验证了所提控制约束方法的有效性.

为了验证本文所提方法的鲁棒性，和文献[13]中未考虑不确定性的最优控制方法进行对比，仿真初始条件均相同，结果表明4个状态最终的误差大小，本文所提方法都要更小，比如初始误差[1 300,130,0.09,11 000]时，本文方法四个状态最终误差为[190,11,0.0048,1 779]，文献[13]方法状态最终误差为[260,25,0.01,3 800].另外在各种误差仿真中，本文方法的性能指标都要更小，上述初始误差下，本文方法性能指标为143.1，文献[13]方法性能指标为164.5.

4 结 论

针对火星进入段模型存在不确定和控制量受约束的情况，本文提出了火星进入段控制量受约束的最优鲁棒制导方法.结合贝尔曼的最优控制理论，并在性能指标中引入饱和函数，得到修正的HJB方程，利用神经网络近似求解修正的HJB方程.仿真结果表明，该方法在系统存在不确定的情况下，可以很好的满足火星进入段的终端条件，控制量也在限制的范围内，为火星进入段制导问题给出了一种有效的方法.

[1] 李爽， 彭玉明， 陆宇平. 火星EDL导航制导与控制技术综述与展望[J]. 宇航学报, 2010, 31(3): 621-627.

LI S, PENG Y M, LU Y P. Review and prospect of mars EDL navigation guidance and control technologies[J]. Journal of Astronautics, 2010, 31(3): 621-627.

[2] 王大轶， 郭敏文. 航天器大气进入过程制导方法综述[J]. 宇航学报， 2015, 36(1)： 1-8.

WANG D Y, GUO M W. Review of spacecraft entry guidance[J]. Journal of Astronautics, 2015, 36(1): 1-8.

[3] 黄飞， 吕俊明， 程晓丽， 等. 火星稀薄大气参数对进入器气动特性的影响[J]. 宇航学报， 2015, 36(10): 1093-1100.

HUANG F, LU J M, CHENG X L, et al. Impact of martian rarefied atmosphere parameters on entry vehicle aerodynamics under hypersonic conditions[J]. Journal of Astronautics, 2015, 36(10): 1093-1100.

[4] BRAUN R D, MANNING R M. Mars exploration entry, descent and landing challenges[J]. Journal of Spacecraft and Rockets, 2007, 44(2)： 310-323.

[5] TOPCU U, CASOLIVA J, MEASE K D. Minimum-fuel powered descent for Mars pinpoint landing[J]. Journal of Spacecraft and Rocktes, 2007, 44(2): 324-331.

[6] SHEN H, SEYWALD H, POWELL R W. Desensitizing the minimum-fuel powered descent for Mars pinpoint landing[J]. Journal of Guidance, Control and Dynamics, 2010, 33(1): 108-115.

[7] LEAVITT J A, MEASE K D. Feasible trajectory generation for atmospheric entry guidance[J]. Journal of Guidance, Control and Dynamics, 2007, 30(2): 473-481.

[8] THORP N A, PIERSON B L. Robust roll modulation guidance for aeroassisted Mars mission[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(2): 298-305.

[9] LU P. Regulation about time-varying trajectories: precision entry guidance illustrated[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(6): 784-790.

[10] BENITO J, MEASE K D. Nonlinear predictive controller for drag tracking in entry guidance[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Washington D.C, AIAA, 2008.

[11] RESTREPO C, VALASEK J. Structured adaptive model inversion controller for Mars atmospheric flight[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(4): 937-957.

[12] BEARD R W, SARIDIS G N, WEN J T. Approximate solutions to the time-invariant Hamilton-Jacobi-Bellman equation[J]. Journal of Optimization Theory and Applications, 1998, 96(3): 589-626.

[13] CHENG T, LEWIS F L, ABU-KHALAF M. A neural network solution for fixed-final time optimal control of nonlinear systems[J]. Automatic, 2007, 43(3)： 482-490.

[14] CHENG T, LEWIS F L, ABU-KHALAF M. Fixed finaltime-constrained optimal control of nonlinear systems using neural network HJB approach[J]. IEEE Transactions on Neural Networks, 2007, 18(6)： 1725-1737.

[15] HADDAD W M, CHELLABOINA V, FAUSZ J L, et al. Optimal non-linear robust control for non-linear uncertain systems[J]. International Journal of Control, 2000, 73(4)： 329-342.

[16] BEARD R. W. Improving the closed-loop performance of nonlinear systems[D]. Troy: Rensselaer Polytechnic Institute， 1995.

MarsOptimalEntryGuidancewithConstrainedControlandUncertainty

LI Maomao

(BeijingInstituteofControlEngineering,Beijing100190，China)

Aiming at the problem of Mars entry guidance, considering the constrained control and uncertainty of Mars atmosphere and detector’s parameters, the optimal robust guidance method with constrained control is proposed. Considering the parameter uncertainty of system, the optimal index of uncertain nonlinear system is transformed into an index of the nominal system. In consideration of the constrained control, a saturated function is introduced, and the guidance problem is transformed into solving the modified HJB equation. The neural network has the ability of approximation. The proposed HJB equation is solved with the neural network because the HJB equation is partial differential equation and there is a great deal of difficulty in solving it. The guidance method makes sure that the uncertain nonlinear systems have an optimal upper bound of performance index and that the method has robustness. Then, the method is applied to the Mars entry guidance. The simulation results show that the terminal conditions of Mars entry phase can be well guaranteed despite uncertainty of system, and that the control is in the constrained range, so the method is effective.

uncertain system; constrained control；HJB equation； Mars entry guidance

2017-02-06

V448

A

1674-1579(2017)05-0007-07

10.3969/j.issn.1674-1579.2017.05.002

李毛毛(1989—)，男，博士研究生，研究方向为航天器导航制导与控制，飞行器再入制导与控制.