初二学生解几何应用题策略类型分析

巨姣丽

摘 要：为了了解初二学生在解几何应用题时的策略类型，对某次的数学测试进行了卷面分析，发现学生的解题策略可以分为俯瞰型、经验型、盲试型三个类型。

关键词：初二学生；几何应用题；策略类型

分析初二学生在解几何应用题时的策略类型，可以帮助教师了解学生的学习情况，并针对不同学生的学习水平，有针对性地进行教学，从而提高整体学生的成绩。

一、俯瞰性

这类学生学习成绩优秀，有着牢固的数学基础，他们在解题过程中能够对题目要求、条件及需要的知识及其之间的关系完整深入地理解掌握，解题目的明确。因为他们对题目理解得比较透彻，所以能够迅速正确地确定所需运用的知识，对题目中已知条件与问题、已知条件与未知关系、中间转换与问题之间的转化过程有清晰的认识，从而很快就能得出解题步骤并验证。

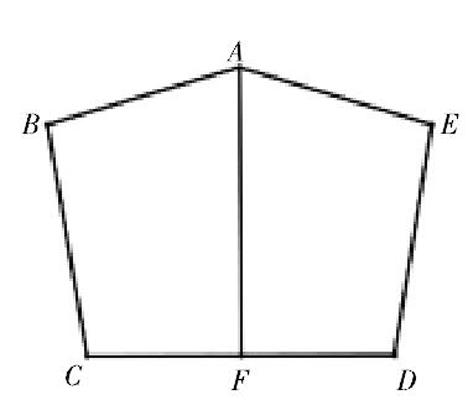
如图，AB=AE，∠ABC=∠AED，BC=ED，点F是CD的中点。求证：AF⊥CD

这类学生在解答上图中的问题时，通过审题可以明确知道这道题考查的是学生对全等三角形的性质与判定及等腰三角形的性质等知识的掌握与灵活运用。學生通过已知条件AB与AE的长度相等，∠ABC=∠AED，所以可以连接AC、AD，得到了三角形ABC和AED，接下来就要想办法证明这两个三角形全等，根据两条边及夹角相等的两个三角形全等可以判定这两个三角形是全等的。根据全等三角形的性质可以得出AC与AD相等，则三角形ACD是等腰三角形，根据等腰三角形底边上的中线垂直于底边的性质，可以判定F作为CD的中点，AF垂直于CD。学生对知识的熟练掌握和运用，使其整个解题思路清晰、顺利、完整，卷面整洁。

学生在读完题目后能够很快了解问题解决所需运用的知识及它们之间的关系，分析整理出题目中的已知条件和隐含条件，选择有用的条件利用相关知识解决问题，有时问题的解决不是一步到位的，这时就要找到中间过渡点来解决问题，可以称为是“俯瞰型”的解题策略。这种学生解题策略的特点是：能够用数学语言描述理解问题；熟练掌握并灵活运用问题、条件、知识的关系，并能熟练创造中间条件以解决问题；能够对解题过程中的各种要素自如地把握调控。

二、经验型

这类学生数学成绩中等，对所学的数学知识有一定的了解掌握，但是对这些知识的理解与掌握还不够灵活，他们没有牢固地掌握数学知识，导致其在做题过程中常常因为遗漏相关知识点而不能顺利正确地解决问题，对知识的掌握不牢固也就进一步使他们对知识的运用不够灵活。这类学生在解决上图中的问题时对三角形全等的性质及判定、等腰三角形的性质没有熟练理解和掌握。他们虽然明白这道题考查的是全等三角形的有关知识，但是在进行问题的转化，创造过渡条件解题时却遇到了困难，在做辅助线的时候出现了问题，他们把B、E连接在一起，想证明由此形成的两个三角形全等，从而使他们的解题过程进入误区，走了弯路，不能顺利清晰地解决问题。还有的学生能够正确地做出辅助线，利用相关知识证明三角形ABC和三角形AED全等，却因为没有熟练掌握等腰三角形ACD的性质，使解题过程遇到了阻碍，不能证明AF垂直于CD。此类学生在解题过程中不能熟练掌握、运用问题、条件、已学知识之间的关系，刻板地依赖以往的学习经验、解题经验，导致解题遇到阻碍。这种解题策略可以称为“经验型”解题策略，具有以下特点：能够运用一定的知识和解题经验把问题条件联系起来进行分析，但是分析过程过于机械化，不能全面地理解问题；不能灵活地掌握问题和条件之间的关系，缺乏对新问题的适应性。

三、盲试型

这类学生的数学成绩和基础都比较差，对数学知识的掌握和运用程度都远远低于以上两种类型的学生，导致其在解答几何应用题时胡乱尝试，进行了大量缺乏意义和依据的推理，导致其解题步骤混乱，卷面不工整。这类学生有的放弃解答上图中的问题，还有的学生在解答这道问题时根据F是CD的中点而得出CF和FD相等的结论，但是这个结论对问题的解决并没有帮助，只是把自己能够推理出的条件盲目地堆积出来，缺乏解决问题的指向性。这种解题策略可以称为“盲试型”解题策略，具有以下特点：缺乏解决问题的目的性、指向性；不能正确认识利用问题、条件、知识之间的关系；通过盲目尝试的方式解题，导致出现没有意义或错误的结果。

教师在几何教学过程中应该采取多种教学方法，加强学生对几何基础知识的理解与掌握，并加大学生的练习，促进学生对知识的灵活运用；在解题过程中要重视解题思路的清晰明确，使学生逐渐形成正确的解题思路；创新题目及解答方法培养学生的创新能力，使学生遇到新问题时能够很好地适应。

参考文献：

[1]张锦坤，连榕.初二学生解几何应用题策略类型的研究[J].心理科学，2007，30（2）：320-324.

[2]袁灵.认知风格对初中生几何应用题解决的影响[D].南京师范大学，2015.

编辑 赵飞飞