酒精折射率与浓度的关系的实验测量

平朔豪 隋娜

摘 要：酒精被广泛地运用于化工、医药、食品和教学实验等领域，浓度是表征酒精的一个重要参量。酒精浓度与折射率有一一对应的关系，在实验上建立它们的关系，可以通过测量折射率来确定酒精的浓度。利用混合液体模型，导出了低浓度的情况下，液体浓度与折射率的非线性关系。在蒸馏水和乙醇折射率相差不大的情况下，线性关系是非线性关系的一个很好的近似，然后用阿贝折射仪测量不同浓度的酒精折射率来检验这个关系。实验结果表明，线性关系拟合给出的结果与混合模型的线性近似结果高度一致。

关键词：酒精折射率；非线性关系；阿贝折射仪

一、模型

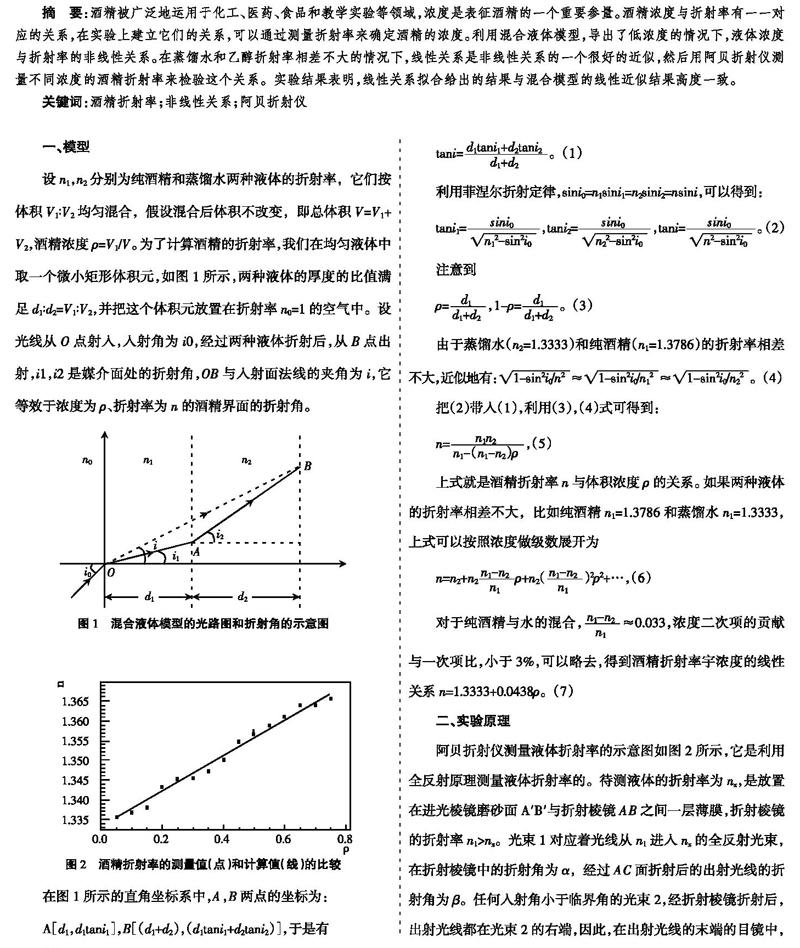
设n1，n2分别为纯酒精和蒸馏水两种液体的折射率，它们按体积V1∶V2均匀混合，假设混合后体积不改变，即总体积V=V1+V2，酒精浓度？籽=V1/V。为了计算酒精的折射率，我们在均匀液体中取一个微小矩形体积元，如图1所示，两种液体的厚度的比值满足d1∶d2=V1∶V2，并把这个体积元放置在折射率n0=1的空气中。设光线从O点射入，入射角为i0，经过两种液体折射后，从B点出射，i1，i2是媒介面处的折射角，OB与入射面法线的夹角为i，它等效于浓度为？籽、折射率为n的酒精界面的折射角。

在图1所示的直角坐标系中，A，B两点的坐标为：

A[d1，d1tani1]，B[（d1+d2），（d1tani1+d2tani2）]，于是有

tani=■。（1）

利用菲涅尔折射定律，sini0=n1sini1=n2sini2=nsini，可以得到：

tani1=■，tani2=■，tani=■。（2）

注意到

？籽=■，1-？籽=■。（3）

由于蒸馏水（n2=1.3333）和纯酒精（n1=1.3786）的折射率相差不大，近似地有：■≈■≈■。（4）

把（2）带入（1），利用（3），（4）式可得到：

n=■，（5）

上式就是酒精折射率n与体积浓度？籽的关系。如果两种液体的折射率相差不大，比如纯酒精n1=1.3786和蒸馏水n1=1.3333，上式可以按照浓度做级数展开为

n=n2+n2■？籽+n2（■）2？籽2+…，（6）

对于纯酒精与水的混合，■≈0.033，浓度二次项的贡献与一次项比，小于3%，可以略去，得到酒精折射率宇浓度的线性关系n=1.3333+0.0438？籽。（7）

二、实验原理

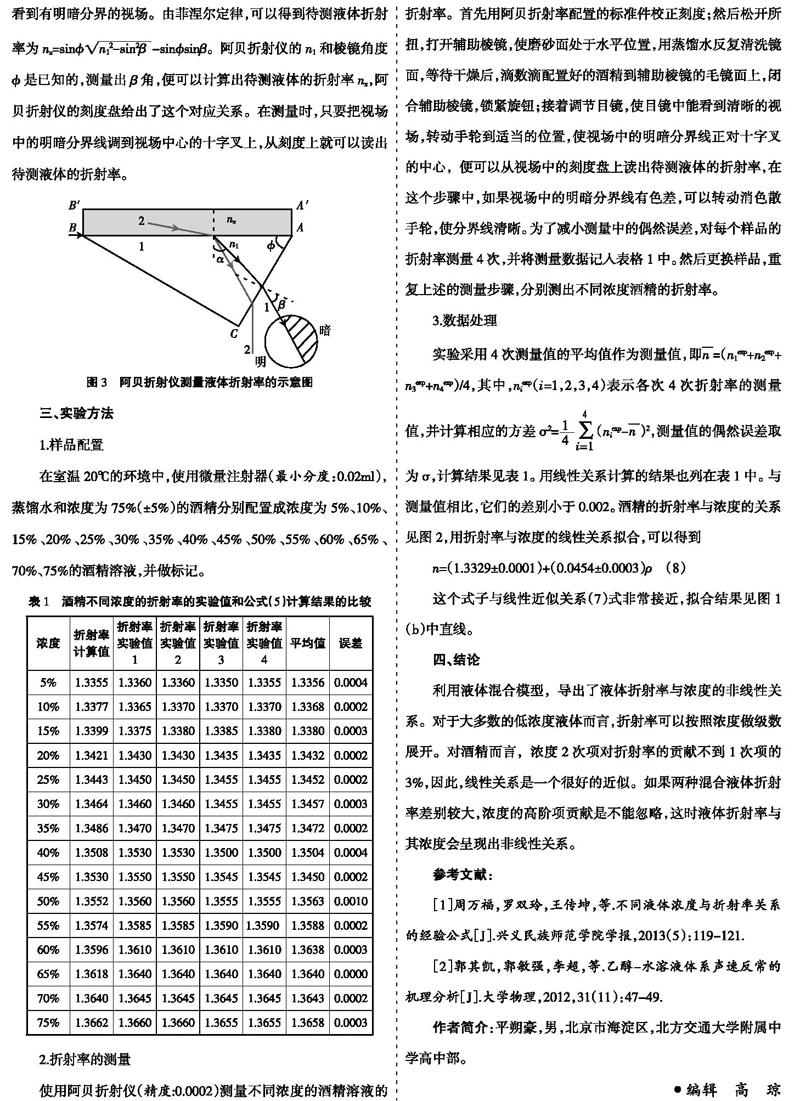
阿贝折射仪测量液体折射率的示意图如图2所示，它是利用全反射原理测量液体折射率的。待测液体的折射率为nx，是放置在进光棱镜磨砂面A′B′与折射棱镜AB之间一层薄膜，折射棱镜的折射率n1>nx。光束1对应着光线从n1进入nx的全反射光束，在折射棱镜中的折射角为？琢，经过AC面折射后的出射光线的折射角为？茁。任何入射角小于临界角的光束2，经折射棱镜折射后，出射光线都在光束2的右端，因此，在出射光线的末端的目镜中，看到有明暗分界的视场。由菲涅尔定律，可以得到待测液体折射率为nx=sin？准■-sin？准sin？茁。阿贝折射仪的n1和棱镜角度？准是已知的，测量出？茁角，便可以計算出待测液体的折射率nx，阿贝折射仪的刻度盘给出了这个对应关系。在测量时，只要把视场中的明暗分界线调到视场中心的十字叉上，从刻度上就可以读出待测液体的折射率。

三、实验方法

1.样品配置

在室温20℃的环境中，使用微量注射器（最小分度：0.02ml）， 蒸馏水和浓度为75%（±5%）的酒精分别配置成浓度为5%、10%、15%、20%、25%、30%、35%、40%、45%、50%、55%、60%、65%、70%、75%的酒精溶液，并做标记。

2.折射率的测量

使用阿贝折射仪（精度：0.0002）测量不同浓度的酒精溶液的折射率。首先用阿贝折射率配置的标准件校正刻度；然后松开所扭，打开辅助棱镜，使磨砂面处于水平位置，用蒸馏水反复清洗镜面，等待干燥后，滴数滴配置好的酒精到辅助棱镜的毛镜面上，闭合辅助棱镜，锁紧旋钮；接着调节目镜，使目镜中能看到清晰的视场，转动手轮到适当的位置，使视场中的明暗分界线正对十字叉的中心，便可以从视场中的刻度盘上读出待测液体的折射率，在这个步骤中，如果视场中的明暗分界线有色差，可以转动消色散手轮，使分界线清晰。为了减小测量中的偶然误差，对每个样品的折射率测量4次，并将测量数据记入表格1中。然后更换样品，重复上述的测量步骤，分别测出不同浓度酒精的折射率。

3.数据处理

实验采用4次测量值的平均值作为测量值，即■=（n1exp+n2exp+n3exp+n4exp）/4，其中，niexp（i=1，2，3，4）表示各次4次折射率的测量值，并计算相应的方差？滓2=■■（niexp-■）2，测量值的偶然误差取为？滓，计算结果见表1。用线性关系计算的结果也列在表1中。与测量值相比，它们的差别小于0.002。酒精的折射率与浓度的关系见图2，用折射率与浓度的线性关系拟合，可以得到

n=（1.3329±0.0001）+（0.0454±0.0003）？籽 （8）

这个式子与线性近似关系（7）式非常接近，拟合结果见图1（b）中直线。

四、结论

利用液体混合模型，导出了液体折射率与浓度的非线性关系。对于大多数的低浓度液体而言，折射率可以按照浓度做级数展开。对酒精而言，浓度2次项对折射率的贡献不到1次项的3%，因此，线性关系是一个很好的近似。如果两种混合液体折射率差别较大，浓度的高阶项贡献是不能忽略，这时液体折射率与其浓度会呈现出非线性关系。

参考文献：

[1]周万福，罗双玲，王传坤，等.不同液体浓度与折射率关系的经验公式[J].兴义民族师范学院学报，2013（5）：119-121.

[2]郭其凯，郭敏强，李超，等.乙醇-水溶液体系声速反常的机理分析[J].大学物理，2012，31（11）：47-49.

作者简介：平朔豪，男，北京市海淀区，北方交通大学附属中学高中部。

编辑 高 琼