单双向两种不同振动模式下黏土强度弱化试验研究

谢琦峰，刘干斌

(宁波大学岩土工程研究所, 浙江 宁波 315211)

单双向两种不同振动模式下黏土强度弱化试验研究

谢琦峰，刘干斌

(宁波大学岩土工程研究所, 浙江 宁波 315211)

以宁波④2层黏土为对象，在单双向两种不同振动模式下，通过不同围压及不同动应力比条件下的动三轴剪切试验，研究宁波软土的动力特性以及振后强度弱化特性。试验结果表明：单向振动模式下(不产生拉应力)产生的动弹性模量衰减、累积塑性应变比双向振动条件下(产生拉应力)的发展显著，但双幅弹性应变发展较弱；在振后剪切阶段，双向振动使得试样产生拉应力，振后抗剪强度弱化比单向振动明显；单向振动模式下，试样发生剪胀，围压越大，剪胀程度减弱直至消失，孔压-轴向应变曲线存在峰值，表现出类超固结土特性；确定了在两种振动模式下，适用于宁波④2层黏土的振后弱化参数。

动三轴试验；振后剪切；振动模式；应力路径；弱化参数

宁波地区的海相沉积软土分布深而广，部分可达100 m，天然含水量高、渗透性差、压缩性大、强度低。随着宁波市轨道交通的发展，深层地下空间被利用，但对宁波深层土体的动力特性以及振后强度弱化特性的试验研究匮乏，对设计时预测隧道的长期沉降带来困难。针对宁波海相沉积软土④2层黏土的动力性状研究，将有助于分析和预测列车荷载作用下轨道交通的沉降和变形稳定。

截至目前，地震荷载、车辆、轨道交通荷载等不同荷载形式作用对软土动力特性的研究成果已很丰富。Seed等[1]根据一系列动三轴试验，提出了孔压的发展模式；Wang等[2]根据上万次振动的动三轴试验，提出了通过孔压推求轴向应变的理论公式；刘干斌[3]等通过一系列温控动三轴试验，探讨温度对软土动力特性的影响，并建立了考虑温度影响的应变本构模型；高博等[4]进行了无规律正弦波振动的动三轴试验，研究了粉土在加卸载过程中动模量的变化规律；范思婷等[5]通过一系列温控动三轴试验，研究温度对软土软化特性的影响并建立了软化模型；叶俊能等[6]针对宁波④2层黏土进行了三轴剪切试验与动三轴试验，研究其静力特性以及动孔压的发展模式，但并未考虑其他动力特性的影响。

现有文献中，对软土振后强度弱化特性进行了大量的试验研究。胡伟等[7]通过静、动三轴试验，得到了考虑孔压发展、剪切应变对黄土的振后抗剪强度的计算公式。高广运等[8]基于高估街黏土不排水强度计算方法，引入损伤应子，提出了振后饱和黏土的强度计算方法及其参数确定。王元战等[9]研究了波浪循环荷载作用下软黏土的强度弱化规律，提出了适用于整个动态循环过程的不排水抗剪强度弱化公式。已有研究成果的重点主要集中在强度弱化的计算上，对不同振动模式下振后抗剪强度特性的对比研究很少。此外，轨道交通隧道穿行于密集的建筑群，产生长期的弱动荷载，在动荷载作用后，软土的不排水抗剪强度对轨道交通的正常运营与维护、上部建筑群的安全使用的影响研究必不可少。

本文选取宁波地区的④2层黏土，在单双向两种不同振动模式下，开展考虑不同围压、动应力比的动三轴试验以及振后三轴剪切试验，获得不同振动模式对深层黏土的动力学特性与强度弱化特性的影响，可以为轨道交通设计和施工提供理论依据。

1 试验概况

选取宁波轨道交通4号线沿线鄞州区④2层黏土，利用温控静动三轴试验仪[10]开展了两种不同振动模式下的动三轴剪切试验。本文采用机械钻孔取样方法，所得原始样直径10 cm，高35 cm；天然含水率(ω)为41.8%，颗粒比重(Gs)为2.74，天然孔隙比(e)为1.227，液限(WL)为43.8%，塑性指数(Ip)为19.6，压缩指数(CC)为0.202，回弹指数(CS)为0.0255。

试验时采用真空饱和法对试样进行饱和，使其饱和度大于95%。振动采用正弦波，频率取1 Hz(计算得到宁波轨道列车的频率约为1.1 Hz)，振次设为10 000 次。其中，所用振动模式分别为单向振动与双向振动，其定义参考Yasuhara[11]，但略有区别：单向振动模式为试样固结完成后，关闭排水阀，预加动应力大小的静偏应力，当孔压与轴向应变稳定，施加动荷载；双向振动为固结完成后，关闭排水阀，即开始施加动荷载。在单向振动时，试样中不产生拉应力，但会受到静偏应力作用，而双向振动条件下，试样会受到拉应力。具体振动模式见图1。

图1 单向双向振动示意图Fig.1 Schematic diagram of one way and two way vibration

当振次达到10 000次后，立即采用应变控制对试样进行剪切，剪切速率为0.5%/min。以上动力试验与剪切试验均在不排水条件下进行。其具体试验方案见表1。

表1 试验方案

2 动力特性试验结果

在不同振动模式下，考虑不同围压σ3、动应力比σd/σ3对试样孔压、累积塑性应变、双幅弹性应变以及动弹性模量的影响，相关参数的计算公式如下：

式中：εd——第N次循环中的双幅弹性应变；

εN,max，εN,min——第N次循环中最大与最小轴向应变；

σd——动应力幅值；

Ed——第N次循环中的动弹性模量；

εp——第N次循环后的累积塑性应变。

根据试验方案(表1)开展不同工况下的动三轴试验，得到饱和黏土试样的孔压、累积塑性应变、双幅弹性应变以及动弹性模量随振次的发展曲线，以动应力比σd/σ3=0.2为例，结果如图2所示。

由图2(a)可知，在相同动应力比条件下，单向振动引起的孔压发展趋势相同，振动初期急剧增大，最后趋于稳定；双向振动引起的孔压发展趋势与单向振动略有差异，振动初期孔压发展较慢，增长速度随振次的增加逐渐减小，但最终孔压并未稳定，仍有孔压累积。经过长期振动后(振次达10 000次时)，围压为100，150，200 kPa，单向振动对应的最终稳定孔压值分别为55.2，51.3，62.9 kPa，孔压归一化值分别为0.552，0.342，0.314；双向振动对应的最终孔压值分别为27.36，42.58，67.66 kPa，归一化值分别为0.274，0.284，0.338。综上所述，同一动应力比条件下，单向振动引起的最终孔压值相差不大，归一化孔压随围压的增大而减小；双向振动引起的最终孔压随围压的增大而增大，归一化孔压也略有增大，但相差不大。单向振动时，试样受到初始静偏应力作用，振动初期孔压发展较双向振动快，最后趋于稳定；双向振动无静偏应力作用，振动初期孔压发展较慢，但试样受到拉应力作用，孔压稳定较慢。

由图2(b)可知，单向振动下，受静偏应力作用，使得累积塑性应变在振动初期急剧发展，随振次的增大，累积塑性应变增长减缓，累积塑性应变的发展趋势比双向振动大，相差一个数量级。同一动应力比时，单向振动所引起的累积塑性应变随围压增大而减小，而双向振动引起的累积塑性应变随围压的增大而增大。单向振动时，归一化孔压随围压的增大而减小，使得归一化有效应力相应增大，使得累积塑性应变减小。双向振动时，归一化孔压随围压的增大而增大，使得归一化有效应力相应减小，使得累积塑性应变增大。

由图2(c)可知，单向振动下，双幅弹性应变随围压的增大而增大；而双向振动下，双幅弹性应变随围压的增大而减小，由有效应力发展的不同导致。双向振动引起的双幅弹性应变比单向振动所产生的略大，且在一定围压范围内，差值随围压的增大而增大。单向振动受到初始静偏应力作用，限制了双幅弹性应变的发展；而双向振动试样会受到拉应力作用，促进双幅弹性应变的发展。

图2 σd/σ3=0.2时动力参数随振次的发展曲线Fig.2 Dynamic parameters vs vibration times on σd/σ3=0.2

在不同振动模式下，动弹性模量随围压的增大而增大；随围压的增大，双向振动引起的动弹性模量增长幅度小于单向振动引起的增量，试样中拉应力的产生促进了动弹性模量的衰减。同一围压下，单向振动产生的动弹性模量比双向振动大，由式(2)的特性就可得知，双向振动产生的双幅弹性应变比单向振动大，因此式(2)计算得到的动弹性模量相应减小。

综上所述，试样受到动荷载作用时，不同的振动模式对试样动力特性有复杂的影响。单向振动的初始静偏应力会促进累积塑性应变的发展，双向振动产生的拉应力会促进动弹性模量与双幅弹性应变的发展。

3 振后强度弱化试验

在动荷载作用后，立即对试样进行不排水三轴剪切试验，研究不同振动模式下，黏土振后孔压、抗剪强度以及应力路径的发展规律。其中，抗剪强度q的计算通过土工试验规范进行修正：

式中：Aa——试样的校正断面积；

A0——试样的初始断面积；

εp——试样轴向应变；

q——试样校正抗剪强度，简称抗剪强度；

q′——轴力计的读数。

当振次达到10 000次后，立即开始三轴剪切试验，得到饱和黏土试样的孔压、抗剪强度随轴向应变的发展曲线，以及应力路径曲线，结果如图3、图4、图6所示。

3.1孔压发展分析

由图3可知，受到动荷载作用后，试样所产生的孔压与正常三轴剪切试验有很大的区别。

图3 孔压随轴向应变发展曲线Fig.3 Curves of pore pressure vs axial strain

由图3(a)可知，试样在正常三轴剪切试验作用下，孔压随轴向应变的增大而增大，最终趋于稳定，围压越高，孔压稳定越快。由图3(b)、图3(c)可以看出，在单向振动模式下，三轴剪切的孔压发展曲线存在峰值点，且动应力比越大峰值越明显；动应力比一定时，围压越大，孔压最大值随之增大，且峰值点逐渐消失，试样逐渐从发生剪胀变为不发生剪胀。而在双向振动模式下，在一定动应力比范围内，孔压发展曲线并未出现峰值点。在两种模式下，围压一定时，稳定孔压值随动应力比的增大而增大；动应力比一定时，稳定孔压值随围压的增大而增大。

3.2抗剪强度发展分析

抗剪强度发展曲线如图4所示，由图4可知，受到动荷载作用后，试样的抗剪强度有不同程度的弱化。由图4(a)可得，试样的抗剪强度-轴向应变曲线，存在峰值点，呈应变软化型；围压越大，峰值点越明显。由图4(b)、图4(c)可知，试样振后抗剪强度-轴向应变曲线呈应变软化型。围压相同时，动应力比增大，振后抗剪强度弱化越明显；动应力比相同时，围压越大，振后抗剪强度越大，且单向振动的抗剪强度大于双向振动。在动荷载作用后，试样孔压累积，有效应力减小，抗剪强度降低。

图4 抗剪强度随轴向应变发展曲线Fig.4 Curves of shear strength vs axial strain curve

参考Yasuhara[11]所提出的振后强度弱化公式：

式中：qcyc——试样振后不排水抗剪强度；

qult——试样不排水抗剪强度；

u——不排水振动荷载产生的孔压；

CC，CS——压缩指数和回弹指数，通过固结试验得到分别为0.202，0.0255；

Λ0——试验参数。

由式(6)可以看出，振后不排水抗剪强度的弱化主要与动荷载作用所产生的孔压有关。将试验方案表1所得的qcyc/qult与u/σ3结果列于表2。

表2 试验结果

将表2试验结果中u/σ3与qcyc/qult绘于u/σ3-qcyc/qult坐标空间中，得到图5。

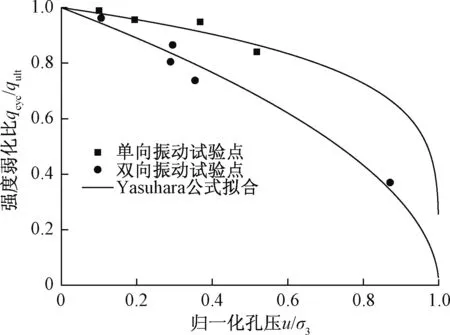
图5 强度弱化比-归一化孔压关系点及其拟合曲线Fig.5 u/σ3-qcyc/qult and its fitting curves

用式(6)对图(5)进行拟合，拟合曲线绘于图5，得到单向振动下试验参数Λ0=0.701，R2=0.842；双向振动下试验参数Λ0=0.419，R2=0.968，拟合效果较好，可为实际工程提供借鉴意义。

由图5可以看出，双向振动作用下强度弱化比单向振动作用下强度弱化比要明显，与现有文献[9]略有差异。在一定动应力比范围内，试样所受的拉应力对试样振后抗剪强度的影响比静偏应力要明显。

3.3应力路径分析

由图6(a)可知，试样临界状态线的M值取0.89。由图6(b)可知，双向振动时，动应力比增大，应力路径左移，形状未发生改变；单向振动时，动应力比增大，应力路径左移的同时，形状逐渐变为折线形。由图6(c)可以看出，动应力比不变，围压越大，应力路径线越接近于不受动荷载作用时的应力路径线。

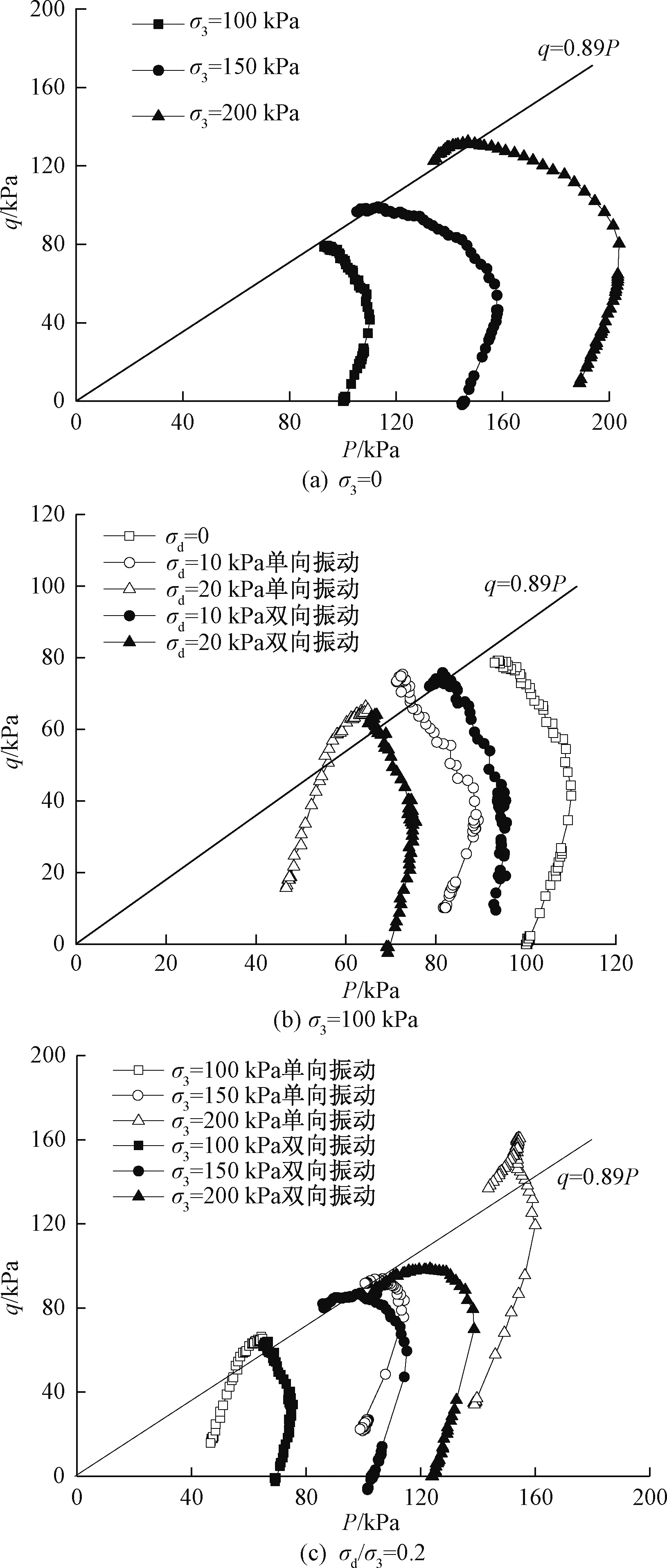
图6 应力路径曲线Fig.6 Stress paths

综上，动荷载作用下试样的M值未改变，均可取为0.89。受到动荷载作用后，试样的应力路径曲线左移、形状发生变化，表现出类固结土的性质。在动荷载作用后，试样孔压累积，有效应力减小，超固结比增大，应力路径线类似于超固结土的应力路径线。

在单向振动模式下，试样各应力路径初始阶段近似平行。双向振动也有相同结论。在不同有效围压下，剪切的初始阶段，外荷载主要由土体骨架承受，与振动产生的孔压大小无关。

4 结论

(1) 试样在不同的振动模式作用下(单向与双向振动)，表现出不同的动力特性。单向振动产生的初始静偏应力会促进累积塑性应变的发展，双向振动产生的拉应力会促进动弹性模量与双幅弹性应变的发展。

(2) 振后剪切阶段，单向振动模式下，孔压-轴向应变曲线存在峰值点，动应力比越大、围压越小，剪胀越明显；双向振动模式下，未出现峰值点。

(3) 在双向振动模式下，试样中产生拉应力，对试样振后不排水抗剪强度的弱化比单向振动明显；参考了Yasuhara的成果，确定了两种振动模式下的适用于宁波④2层黏土的试验参数，为轨道交通的设计维护提供参考。

(4) 在两种振动模式作用后，孔压累积，有效围压减小，试样的三轴剪切表现出超固结土的特性，动应力比越大、围压越小，类超固结性越明显。

[1] Seed H B, Martin P P, Lysmer J. Pore-water pressure changes during soil liquefaction[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1976, 102(Proc. Paper# 12074).

[2] Wang J, Guo L, Cai Y Q,etal. Strain and pore pressure development on soft marine clay in triaxial tests with a large number of cycles[J]. Ocean Eng，2013，74:125-132.

[3] 刘干斌, 范思婷, 陈斌, 等. 考虑温度影响的饱和软黏土累积变形特性研究[J]. 岩土工程学报, 2016, 38(7): 1238-1245.[LIU G B, FAN S T, CHEN B,etal. Characteristics of cumulative deformation of saturated soft clay considering temperature effect[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1238-1245. (in Chinese)]

[4] 高博,张鸿儒.邯郸与太原两地粉土动力特性的试验研究[J]. 工程地质学报, 2008, l6(4): 502-506.[GAO B, ZHANG H R. Cyclical tri-axial tests for dynamic modulus characteristics of silty soils at six sites in Handan and Taiyuan[J]. Journal of Engineering Geology, 2008, 16(4): 502-506. (in Chinese)]

[5] 范思婷, 刘干斌, 陈斌, 等. 考虑温度影响的饱和软黏土应变软化研究[J]. 振动与冲击, 2017, 36(6): 1-6.[FAN S T, LIU G B, CHEN B,etal. Study on strain softening of saturated soft clay considering temperature effect[J]. Journal of Vibration and Shock, 2017, 36(6): 1-6. (in Chinese)][6] 叶俊能, 陈斌. 海相沉积软土动强度与孔压特性试验研究[J]. 岩土力学, 2011,32(增刊1): 55-60.[YE J N, CHEN B. Dynamic strength and pore pressure property of marine deposit soft clay[J]. Rock and Soil Mechanics, 2011,32(Sup 1): 55-60. (in Chinese)]

[7] 胡伟, 黄义, 刘增荣. 循环荷载下饱和黄土不排水强度退化规律试验与理论研究[J]. 岩土力学, 2009, 30(10): 2996-3000.[HU W, HUANG Y, LIU Z R. Testing and theoretical study of undrained shearing strength of saturated loess under cyclic loading[J]. Rock and Soil Mechanics, 2009, 30(10): 2996-3000.(in Chinese)]

[8] 高广运, 顾中华, 杨宏明. 循环荷载下饱和黏土不排水强度计算方法[J]. 岩土力学, 2004,25 (增刊2): 379-382.[GAO G Y, GU Z H, YANG H M. A calculation method for un drained strength of saturated clay under cyclic loads[J]. Rock and Soil Mechanics, 2004,25 (Sup 2): 379-382. (in Chinese)]

[9] 王元战, 杨攀博, 孙熙平, 等. 循环荷载下软黏土强度弱化研究及其动力计算应用[J]. 岩土工程学报, 2015, 37(5): 821-828.[WANG Y Z, YANG P B, SUN X P,etal. Strength weakening of soft clay under cyclic loading and its dynamic calculation[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(5): 821-828. (in Chinese)]

[10] 黄勇，刘干斌，祁良,等. 不同温度下饱和软黏土应力路径试验研究[J]. 水文地质工程地质, 2016, 43(2): 83-87.[HUANG Y, LIU G B, QI L,etal. Experimental study of the stress path of saturated soft clay under different temperatures[J]. Hydrogeology & Engineering Geology, 2016, 43(2): 83-87.(in Chinese)]

[11] Yasuhara K, Hirao K, Hyde A F L. Effects of cyclic loading on undrained strength and compressibility of clay[J]. Soils and Foundations, 1992, 32(1): 100-116.

责任编辑：张明霞

Anexperimentalstudyofthestrengthweakeningcharacteristicsofclayundertwodifferentvibrationmodes

XIE Qifeng, LIU Ganbin

(InstitutionofGeotechnicalEngineering,NingboUniversity,Ningbo，Zhejiang315211,China)

Cyclic triaxial tests and post-triaxial shear tests of the Ningbo clay are carried out to examine the effects of different vibration states, confining pressures and dynamic stress ratios on the dynamic characteristics and the post-vibration strength weakening characteristics of soil. The results show that the development of dynamic elastic modulus and cumulative plastic strain under one-way loading (no tensile stress) is more significant than that under two-way loading (resulting in tensile stress). But the development of elastic strain is opposite. In the shear stage, there is a peak at the pore pressure-axial strain curve and shear dilatation of the specimen, which shows the characteristics of the over-consolidated soil. Decrease in the shear strength under two-way loading is more obviously than that under one-way loading because of the tensile stress. The post-vibration strength weakening parameters under two vibration mode of the Ningbo ④2clay are determined.

cyclic triaxial test; post-vibration shear; vibration mode; stress path; strength weakening parameters

TU411.7

A

1000-3665(2017)05-0066-06

10.16030/j.cnki.issn.1000-3665.2017.05.11

2017-04-02;

2017-05-05

国家自然科学基金项目资助(51478228)；浙江省新苗人才计划资助(2016R405074)

谢琦峰(1992-)，男，硕士，主要从事土动力方面的研究。E-mail: 2290443897@qq.com