宁波土层的流变固结试验及流变模型参数研究

邓岳保，陈 菲，刘干斌，叶俊能

(1.宁波大学岩土工程研究所，浙江 宁波 315211；2.宁波市轨道交通工程建设指挥部，浙江 宁波 315012)

宁波土层的流变固结试验及流变模型参数研究

邓岳保1，陈 菲1，刘干斌1，叶俊能2

(1.宁波大学岩土工程研究所，浙江 宁波 315211；2.宁波市轨道交通工程建设指挥部，浙江 宁波 315012)

固结与流变特性及其参数取值研究是软基上结构物长期沉降课题的重要组成部分。针对宁波轨道交通工程的两个典型土层，开展了基于GDS固结仪的流变固结试验，获得了土样的主固结与次固结性状参数。采用Gibson三元件流变模型结合Matlab软件的拟合功能，得到了土样的三元件流变模型参数。通过对试验结果进行分析总结，发现宁波软土的次固结过程表现出较明显的非线性。次固结系数Ca与压缩指数Cc近似符合Ca/Cc=0.02±0.01。宁波软土的一维流变过程符合Gibson三元件流变模型规律，且其模量参数和黏滞系数均随固结压力的增大而增大。

GDS固结仪；流变固结；次固结；流变模型；参数取值

室内试验和工程实践表明，岩土类材料往往具有明显的流变特性，即：土体的变形和强度特性除了与应力有关之外，还与时间有关[1]。岩土工程中时常出现的工后沉降大甚至失稳破坏等问题与岩土的流变性密切相关。流变固结试验是研究土体流变特性的方法之一。通过开展该试验，可以分析研究土体的固结与流变特性，进而发展适用于结构物长期沉降分析的理论[2～3]。目前，关于土体流变特性的试验研究已有不少成果[4～10]，但是关于土体流变固结参数的取值经验相对缺乏。

宁波是浙江省第二大城市和长江三角洲南翼经济中心。宁波市区地势低平，海相沉积软土层分布十分广泛，且厚度不均。近年来，宁波开始了轨道交通建设，轨道1号线于2014年6月正式投入运营。由于轨道交通建设的施工扰动，以及列车荷载的长期作用，轨道交通长期沉降问题成为建设单位和工程单位非常关心的问题。

受宁波轨道交通项目委托，开展了基于GDS固结试验仪的宁波典型土层流变固结试验研究。本文将对试验过程和成果进行介绍，给出三元件流变模型参数的确定方法，以期获得该地区土样的固结流变特性，并为依托工程的长期变形分析提供参数取值依据。

1 试验土样与仪器

试样取自宁波轨道二号线一期工程江北段和海曙段，共5个土层。各土层土性情况及取样深度见表1。本试验依托浙江大学软弱土与环境土工教育部重点试验室平台展开。试验测试内容包括固结渗透联合分级加载试验、CRS固结试验和流变固结试验。试验方法主要参考了《土工试验方法标准》(GB/T 50123—1999)和GDS固结渗流联合试验操作手册。关于GDS固结渗透联合试验仪的软、硬件介绍可参考有关文献[2]，此处不再赘述。试验步骤简介如下：(1)试样制备，测试土样三相指标：密度、含水量、比重，获得土样初始孔隙比；(2)试样安装与排气，其中排气阶段包括轴压室排气、反压口排气和底部压力口排气；(3)试验软件设定与初始化，位移传感器和压力室清零；(4)试样饱和，在不同围压级别下进行饱和；(5)试验开始，监测与记录试验数据；(6)试验结束，处理试验数据。

在开展流变固结试验之前，通过常规的室内土工试验测试，得到了各土层试样的基本物理力学指标(平均值)，如表1所示。其中，物理量Cc和Ck分别为土体的压缩指数和渗透指数。

表1 试验土样及其基本物理力学指标

2 流变固结试验

针对黏土②-1(基坑开挖层)和粉质黏土③-2(约20 m深度，地铁隧道穿越层)，开展一维流变固结试验。

2.1黏土样②-1试验

2.1.1试验过程

设置3个加载步进行试样反压饱和，饱和有效应力为20 kPa。考虑到土样取样深度在10 m以内，设置固结围压为100 kPa。3个加载步对应的轴向压力和反压分别为：P1=30 kPa，P2=10 kPa；P1=70 kPa，P2=50 kPa；P1=120 kPa，P2=100 kPa。试样饱和后进行分级加载试验，其有效荷载分别为100，300 kPa。试验过程中，每级加载时间设置为5 000 min。

2.1.2固结系数确定

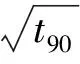
表2 黏土试样压缩性质试验结果

其中，H是最大排水距离(单面排水时等于h；双面排水时等于h/2)。其中土样高度h=(h1+h2)/2，即某级固结压力作用下，初始试样高度h1和终了试样高度h2的平均值。

2.1.3次固结系数确定

次固结系数Ca根据e-lgt曲线得到。本次试验研究表明，黏土在主固结完成之后，土样变形随时间变化曲线在e-lgt曲线上表现为一直线。该直线的斜率即为次固结系数。次固结系数计算式如下：

图1为黏土试样在两级荷载作用下的e-lgt曲线，据此可确定主次固结门槛时间。表3为次固结系数成果。

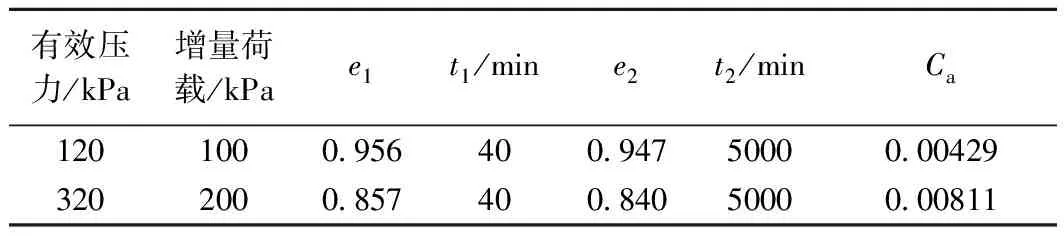
表3 黏土次固结系数结果

2.2粉质黏土样③-2试验

2.2.1试验过程

设置3个加载步进行试样饱和，饱和荷载为20 kPa。3个加载步对应的轴向压力和反压分别为：P1=70 kPa，P2=50 kPa；P1=120 kPa，P2=100 kPa；P1=220 kPa，P2=200 kPa。试样饱和后进行分级加载试验。因为土样取自20 m深度处，取围压为200 kPa。

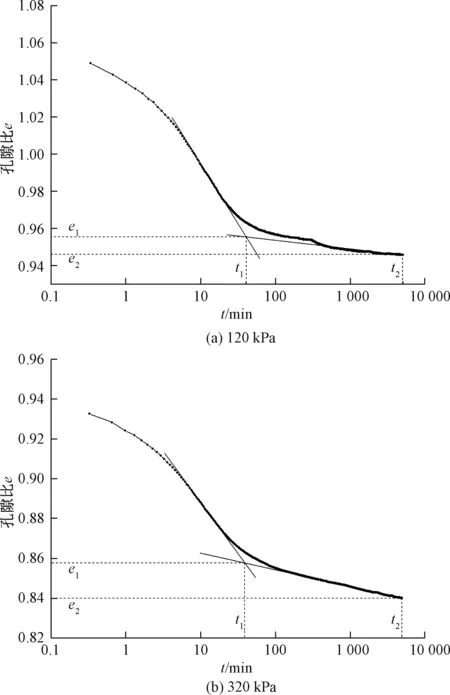
图1 黏土试样在不同压力作用下的e-lgt曲线Fig.1 Curve of e-lg t for the clay sample

分级加荷分别为50，100，200，400，800 kPa。

2.2.2固结系数与次固结系数确定

粉质黏土试样在各级荷载下压缩性指标结果见表4。固结系数确定方法同前文，次固结系数计算方法亦同前文。表4中给出了粉质黏土试样的固结系数和次固结系数最终结果。

表4 粉质黏土试样压缩性质试验结果

3 流变模型参数确定

3.1流变模型

在岩土工程数值分析和理论计算中，优选流变模型的参数非常关键。国内外学者对此进行了研究[2]。在此介绍Gibson和Lo于1962年曾提出一种确定流变模型参数的方法。

Gibson采用的模型为三元件流变模型。该模型所描述土体的应力应变关系为：

当孔压消散后：

式中：ta——孔压消散时间或主固结完成时间。

上述三元件模型中，模量E0根据单级加载作用下最终沉降s∞获得；另外2个参数模量E1和黏滞系数η通过拟合常有效应力荷载作用下变形量s(t)和时间t变化的对数曲线来确定：

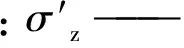
3.2黏土流变参数

黏土试样流变固结试验发现，各级荷载作用1 440 min后主固结基本结束(注：对e-lgt曲线后半段进行线性拟合；拟合直线的起始时间处土体主固结过程完成)。下文按Gibson方法进行数据处理。首先，由变形时间曲线获得各级荷载下y-t曲线(图2)。由图2发现，y-t曲线线性相关性较好。基于此，利用MATLAB拟合工具箱中的线性函数对各曲线进行拟合。根据上述拟合结果并按公式(5)进行处理，可得到各级增量荷载情况下的流变模型参数(表5)。

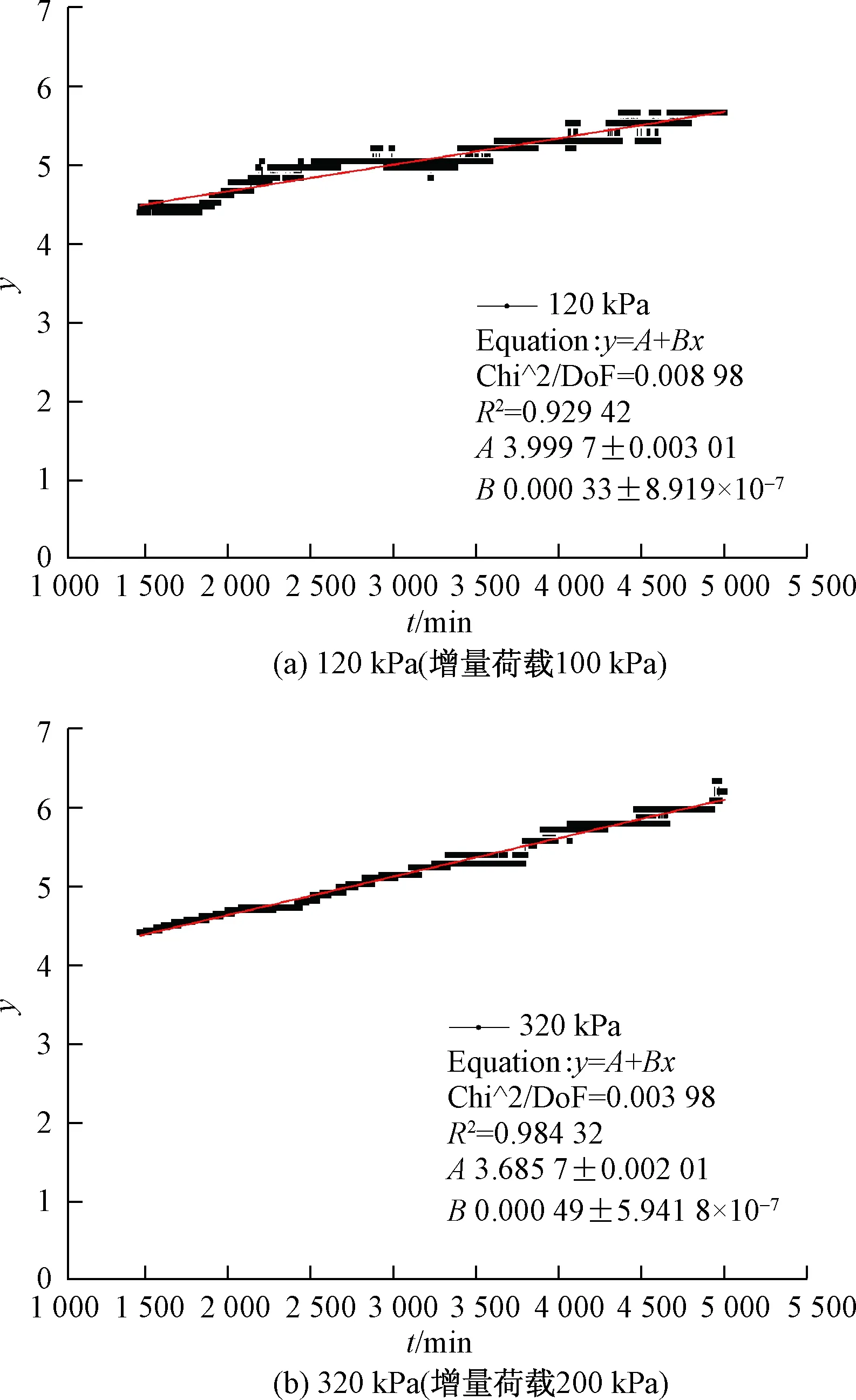
图2 不同荷载下y-t曲线及其拟合情况Fig.2 Deformation-time curve and the fitting curve (clay)

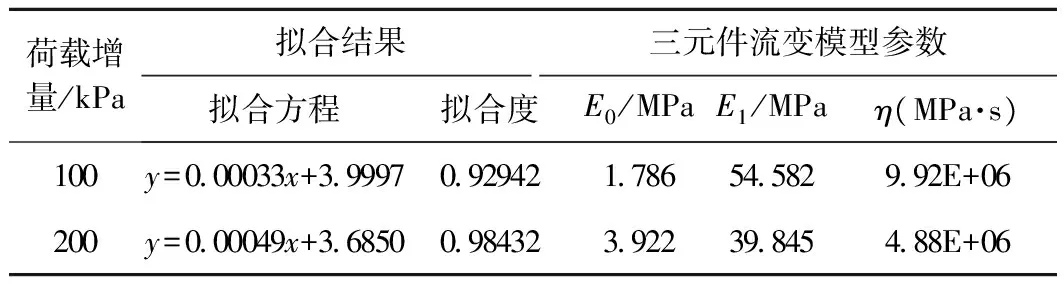
荷载增量/kPa拟合结果三元件流变模型参数拟合方程拟合度E0/MPaE1/MPaη(MPa·s)100y=000033x+39997092942178654582992E+06200y=000049x+36850098432392239845488E+06

3.3粉质黏土流变参数

试验发现，各级荷载作用333 min以后主固结已基本完成。按前文方法进行数据处理，图3为各级常有效应力作用下y-t曲线。由图3可见，各级荷载作用下y-t曲线基本呈线性关系，并且斜率大致相等。根据上述试验情况，选择采用Gibson三元件流变模型进行曲线拟合，并通过在MATLAB中编制程序来实现。拟合过程中，程序设定了固定的曲线斜率。汇总上述拟合结果，得到各加载步情况下的流变模型参数。表6为y-t曲线拟合情况及流变模型参数计算结果。由表6可知，除50 kPa荷载情况外，其余加载情况下拟合效果均较好，相关系数均在0.98以上。

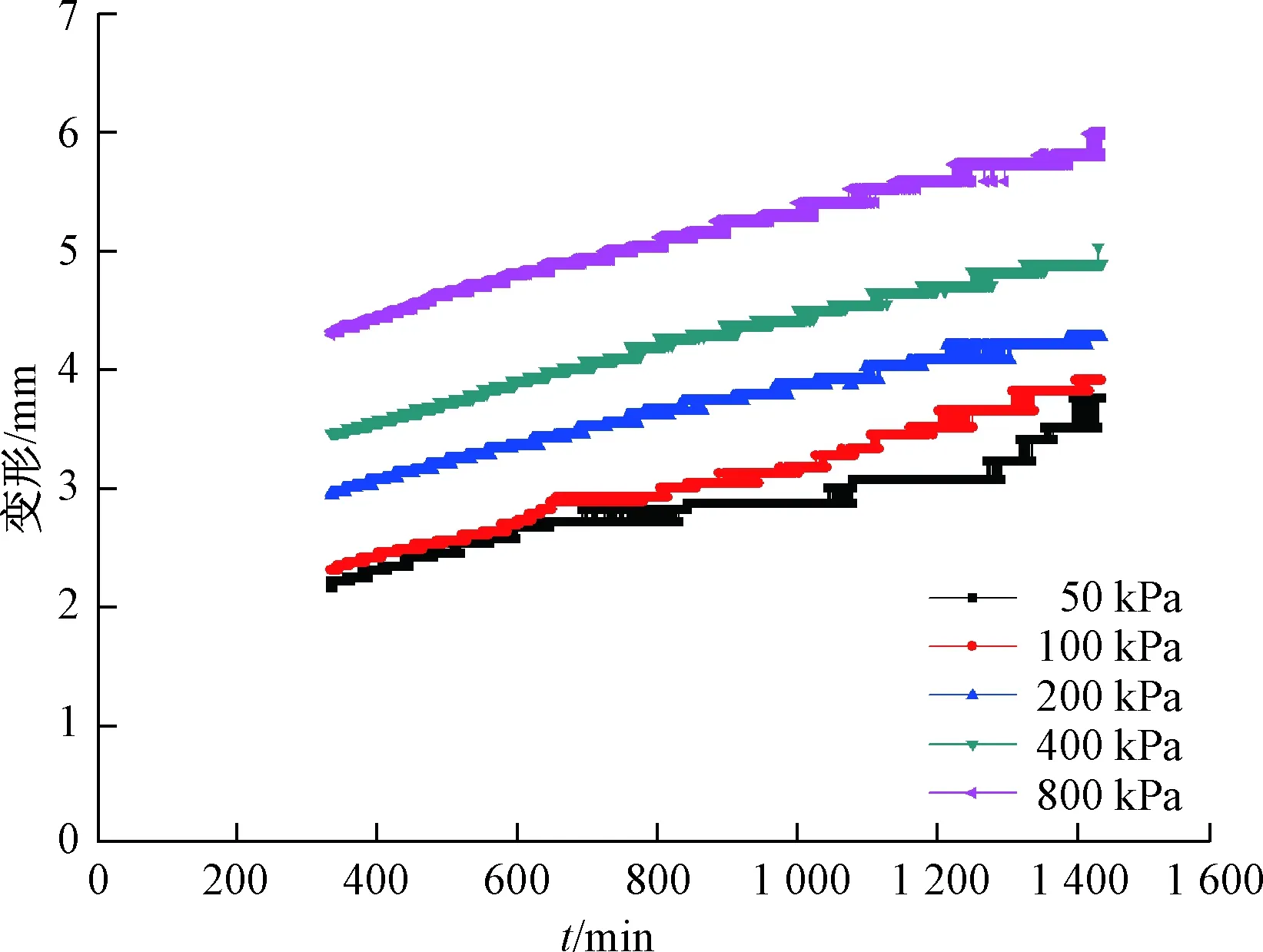
图3 按Gibson方法绘制的变形-时间曲线Fig.3 Deformation-time curve with the Gibson method

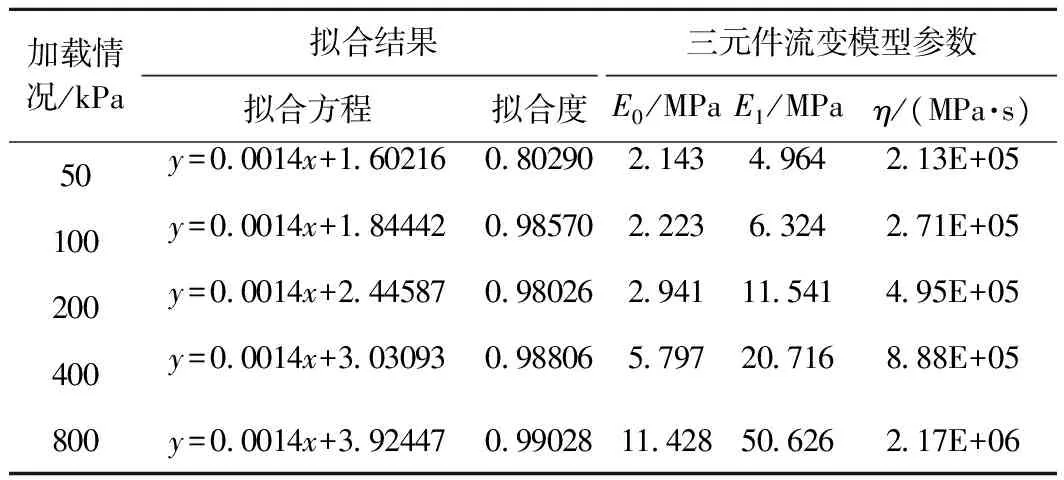
加载情况/kPa拟合结果三元件流变模型参数拟合方程拟合度E0/MPaE1/MPaη/(MPa·s)50y=00014x+16021608029021434964213E+05100y=00014x+18444209857022236324271E+05200y=00014x+244587098026294111541495E+05400y=00014x+303093098806579720716888E+05800y=00014x+3924470990281142850626217E+06

4 试验成果分析

4.1次固结系数与固结压力关系

传统土力学认为土体的次固结系数为一常数。随着研究深入，逐渐认识到次固结系数会受固结压力等因素的影响，次固结过程表现出一定的非线性。余湘娟等[11]对汕头软土的试验表明，当固结压力足够大时次固结系数基本保持恒定，刘用海[12]对宁波软土的试验表明，正常固结黏土的次固结系数随固结压力增大而增大，雷华阳等[13]对天津软土的试验发现，正常固结软土次固结系数随固结压力增大而逐渐降低，但汉波[1]研究温州黏土特性发现，当土体处于超固结状态时，次固结系数随固结压力增大而增大；当土体完全处于正常固结状态后，次固结系数基本无太大变化。

本次试验得到的结果如图4所示。由图4可知，在200 kPa之前，次固结系数随固结压力增大而增大；在200 kPa之后，次固结系数略有衰减。值得说明的是，本次试验粉质黏土试样埋深为20 m，200 kPa的临界压力与该土样的先期固结压力接近。

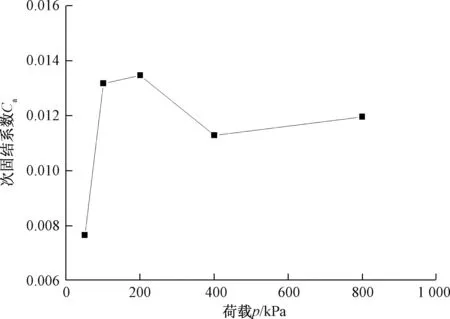
图4 宁波粉质黏土次固结系数随荷载变化曲线Fig.4 Curve of Ca with loading p for the Ningbo silty clay

4.2次固结系数Ca与压缩指数Cc的关系

Walker等[4]首先发现Ca与Cc之间近似满足Ca/Cc=0.025关系。Mesri等[5]总结了22种黏土次固结试验后指出，对于同一种原状黏土，Ca/Cc基本为一常数，其值在0.025～0.10。随后Mesri等[6]进一步指出，对于多数无机质软黏土，Ca/Cc=0.04±0.01；对于高塑性有机质软黏土，Ca/Cc=0.05±0.01。本文通过对但汉波的研究[1]进行补充，结果见表7。

4.3流变模型参数与荷载关系

图5为粉黏③-2的流变参数随荷载变化情况。由图5可知，流变模型参数均随荷载增大而增大，且该趋势随荷载增大而变得明显。由此表明，宁波土层在恒定荷载作用下，其一维流变固结会逐渐趋于稳定。

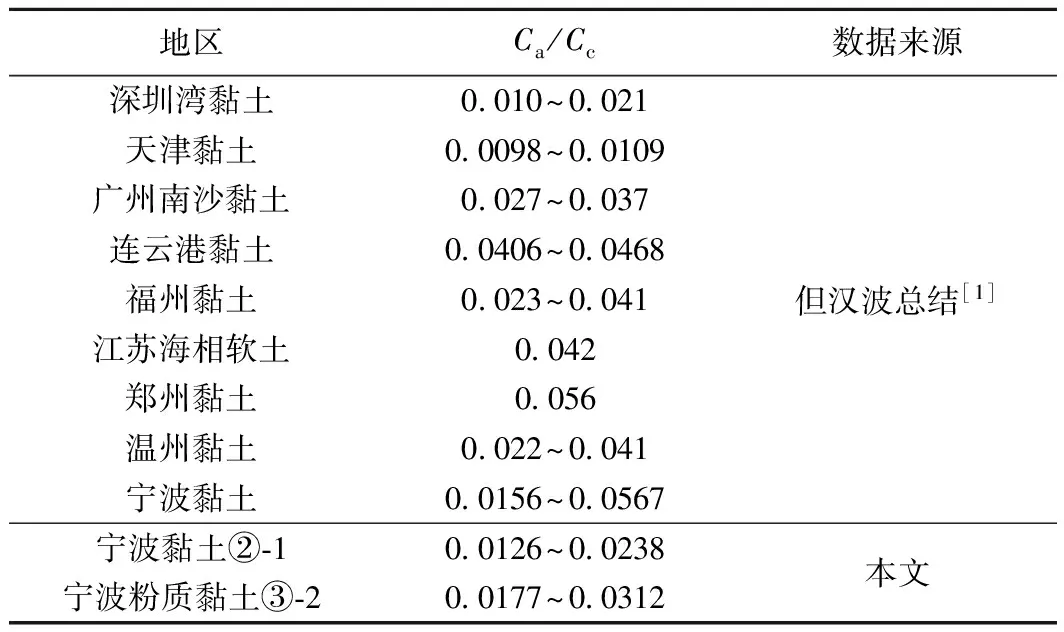
表7 我国部分地区软土的Ca/Cc值

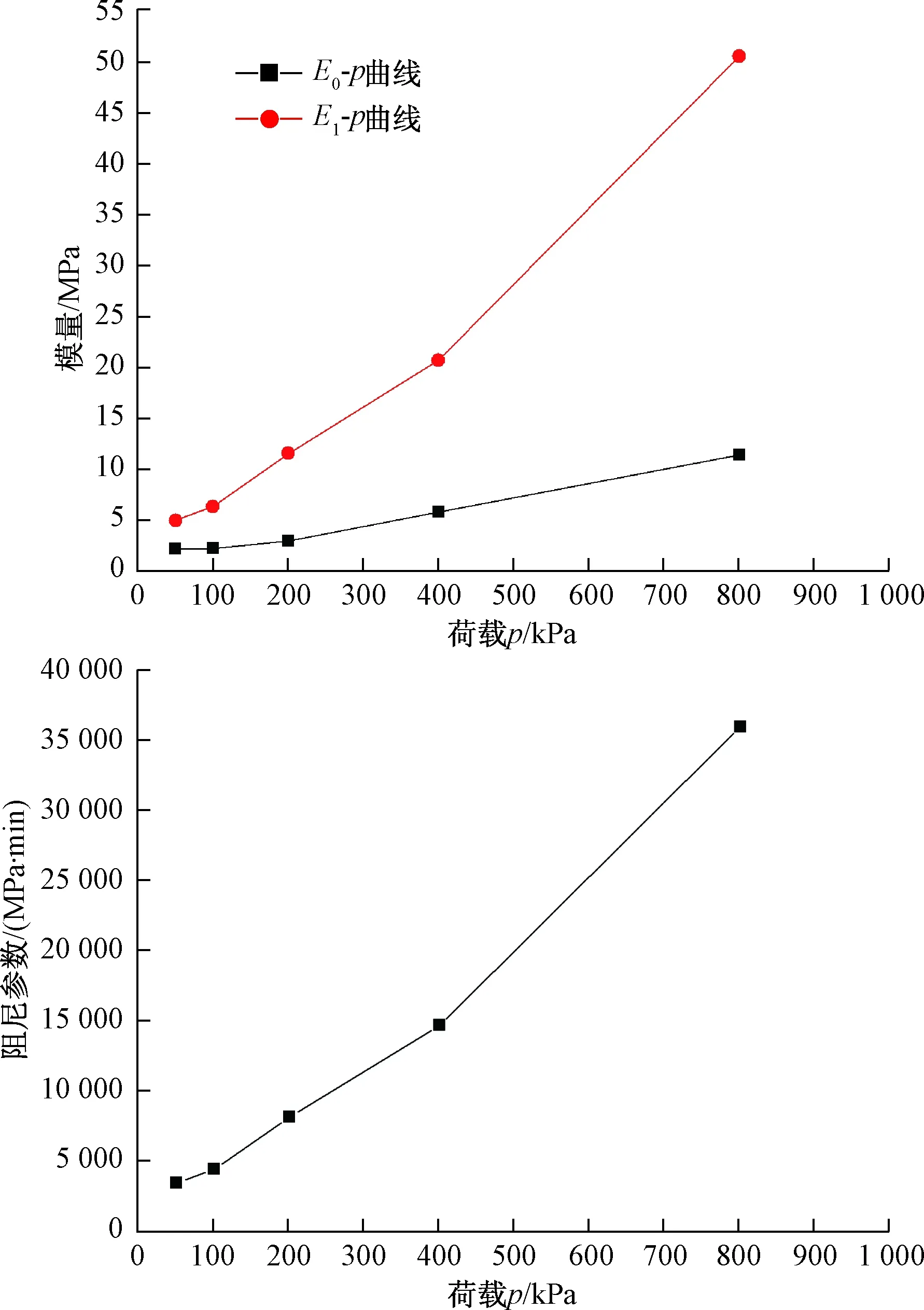
图5 流变模型参数随荷载变化情况Fig.5 Changes in the rheological model parameters with loading

5 结论

(1)宁波软土的次固结过程表现出较明显的非线性；在超固结状态，次固结系数随固结压力增大而增大；当固结压力超过先期固结压力后，次固结系数略有减小。

(2)有限的试验数据表明，宁波软土次固结系数Ca与压缩指数Cc的关系：黏土②-1，Ca/Cc=0.0126～0.0238；粉质黏土③-2，Ca/Cc=0.0177 ～ 0.0312。汇总可近似得到：Ca/Cc=0.02±0.01。

(3)在不同固结压力作用下，宁波典型软土层的一维流变均可用Gibson三元件流变模型来拟合。

(4)宁波典型土层流变模型的模量参数和黏滞系数均随固结压力的增大而增大。

[1] 但汉波. 天然软黏土的流变特性[D]. 杭州: 浙江大学, 2009.[DAN H B. Time Dependent Behavior of Natural Soft Clays[D]. Hangzhou: Zhejiang University, 2009. (in Chinese)]

[2] 李西斌，谢康和，陈福全. 考虑软土流变特性和应力历史的一维固结与渗透试验[J]. 水利学报, 2013,44(1):18-25.[LI X B, XIE K H, CHEN F Q. One dimensional consolidation and permeability tests considering stress history and rheological characteristic of soft soils[J]. Journal of Hydraulic Engineering, 2013, 44(1): 18-25. (in Chinese)]

[3] 曹文贵, 印鹏, 贺敏, 等. 考虑实测数据新旧程度的工后沉降单项模型预测方法[J]. 水文地质工程地质, 2015,42(6):65-70.[CAO W G，YIN P，HE M，etal. A prediction method for post-construction settlement of a single model with the consideration of the new or old degree of the measured data[J]. Hydrogeology & Engineering Geology, 2015,42(6):65-70. (in Chinese)]

[4] Walker L. Undrained creep in a sensitive clay[J]. Geotechnique, 1969, 19(4): 515-529.

[5] Mesri G, Godlewski P M. Time and stress-compressibility interrelationship[J]. Journal of the Geotechnical Engineering Division, ASCE, 1977, 103(5): 417-430.

[6] Mesri G, Castro A.Ca/Ccconcept andK0during secondary compression[J]. Journal of the Geotechnical Engineering, 1987, 113(3): 230-247.

[7] 殷宗泽，张海波，朱俊高，等. 软土的次固结[J].岩土工程学报，2003，25(5)：521-526.[YIN Z Z, ZHANG H B, ZHU J G,etal. Secondary consolidation of soft soil[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5):521-526. (in Chinese)]

[8] 张军辉，缪林昌，黄晓明. 连云港软黏土次固结变形研究[J].水利学报, 2005, 36(1)：116-119.[ZHANG J H, MIAO L C, HUANG X M. Study on secondary consolidation deformation of soft clay[J]. Journal of Hydraulic Engineering, 2005,36(1):116-119. (in Chinese)]

[9] 周秋娟，陈晓平.软土次固结特性试验研究[J].岩土力学，2006，27(3)：404-408.[ZHOU Q J, CHEN X P. Test study on properties of secondary consolidation of soft soil[J]. Rock and Soil Mechanics, 2006, 27(3):404-408. (in Chinese)]

[10] 冯志刚，朱俊高. 软土次固结变形特性试验研究[J].水利学报，2009，40(5)：583-588.[FENG ZG, ZHU J G. Experimental study on secondary consolidation behavior of soft soils[J]. Journal of Hydraulic Engineering, 2009, 40(5):583-588. (in Chinese)]

[11] 余湘娟，殷宗泽，董卫军.荷载对软土次固结影响的试验研究[J].岩土工程学报,2007,29(6):913-916.[YU X J, YIN Z Z, DONG W J. Influence of load on secondary consolidation deformation of soft soils[J]. Chinese Journal of Geotechnical Engineering,2007,29(6):913-916.(in Chinese)]

[12] 刘用海.宁波软土工程特性及其本构模型应用研究[D].杭州:浙江大学，2008.[LIU Y H. Study on engineering property and application of constitutive of model for Ningbo soft clay[D]. Hangzhou: Zhejiang University, 2008. (in Chinese)]

[13] 雷华阳，肖树芳.天津软土的次固结变形特性研究[J].工程地质学报，2002, 10(4): 385-389.[LEI H Y, XIAO S F. Study on secondary-consolidation deformation characteristics of soft soil in Tianjin[J]. Journal of Engineering Geology, 2002, 10(4):385-389. (in Chinese)]

责任编辑：张明霞

AstudyoftherheologicalconsolidationtestandrheologicalmodelparametersfortheNingbosoillayer

DENG Yuebao1，CHEN Fei1，LIU Ganbin1，YE Junneng2

(1.InstituteofGeotechnicalEngineering,NingboUniversity,Ningbo,Zhejiang315211,China; 2.NingboUrbanRailTransitProjectConstructionHeadquarter,Ningbo,Zhejiang315012，China)

Consolidation and rheological properties of soft soil and their values are important parts of the researches of long-term settlement of structures on soft ground. A series of rheological consolidation tests for two typical soil samples in the Ningbo Rail Transit project are carried out based on the advance GDS consolidation test system. Parameters of the primary consolidation and secondary consolidation behaviour of soft soil are obtained based on the test. On the basis of the introduction of a three components rheological model (Gibson model), the model parameters for the three components rheological model are obtained by using the Matlab fitting method. The results indicate that the secondary consolidation behaviour of the Ningbo soft soils exhibit obvious nonlinear properties; the secondary consolidation coefficient is approximately in linear relation to the compression index and there isCa/Cc=0.02±0.01; the one-dimensional rheological consolidation behavior for the Ningbo soft soil agrees with the Gibson’s three components rheological model; the modulus and viscosity coefficient of the rheological model increase with the increasing consolidation pressure.

GDS consolidation test system; rheological consolidation; secondary consolidation; rheological model; parameters determination

TU411.5

A

1000-3665(2017)05-0046-06

10.16030/j.cnki.issn.1000-3665.2017.05.08

2017-02-07;

2017-04-26

浙江省自然科学基金项目资助(LY17E080008)；国家自然科学基金项目资助(51308309)

邓岳保(1983-)，男，博士，副教授，主要从事岩土与地下工程等领域的教学与科研工作。E-mail：dengyuebao@nbu.edu.cn