TLP平台NODE结构确定性疲劳与疲劳可靠性对比分析

梁园华，高 明，韦斯俊，杨清峡

(1.中国船级社 海工技术中心，北京 100007; 2.北京数码易知科技发展有限责任公司，北京 100007)

TLP平台NODE结构确定性疲劳与疲劳可靠性对比分析

梁园华1，高 明2，韦斯俊2，杨清峡1

(1.中国船级社 海工技术中心，北京 100007; 2.北京数码易知科技发展有限责任公司，北京 100007)

TLP平台的疲劳计算在工程中常采用确定性疲劳计算方法，但是影响结构疲劳的大多数因素都是随机的，确定性的方法很难对这些因素做出客观的描述。因此，本文基于谱疲劳方法，分别采用确定性疲劳和疲劳可靠性对TLP平台NODE结构进行疲劳筛选计算，并对计算结果进行对比分析。结果显示NODE结构局部区域不满足疲劳强度要求，相比于疲劳可靠性，确定性疲劳方法更加保守。

张力腿平台；确定性疲劳；疲劳可靠性；谱疲劳；疲劳寿命；可靠性指标

海洋平台的疲劳失效后果往往很严重[1-2]，因此，在设计中需要保证结构有足够的疲劳强度。通常，结构的疲劳损伤和疲劳寿命采用S-N曲线和Miner线性累积损伤理论来计算。近年来断裂力学也得到了应用。但是这两种方法都是在确定性的意义上使用的，即分析过程中有关参数都有确定的数值。而事实上，海洋工程结构疲劳分析中大多数的影响因素从本质上讲都是随机的，因此，疲劳可靠性的方法在海洋工程结构的疲劳分析中也得到越来越多的研究和应用。

对于海洋工程结构疲劳的确定性方法和可靠性方法，国内外都进行了大量研究。刘刚等[3]采用热点应力，结合S-N曲线及Miner线性累积损伤准则对BINGO9000钻井平台管节点结构进行了疲劳计算。张剑波[4]同样采用热点应力法对半潜式钻井船进行了疲劳寿命计算，并对危险节点进行了可靠性分析和裂纹扩展分析。陈伯真、胡毓仁[5]研究了液化体船液舱结构疲劳可靠性问题，并给出了用一阶二次矩方法计算液舱疲劳寿命可靠度的迭代过程。此外，二人根据模糊集合理论的基本原理，在海洋结构管节点的疲劳可靠性分析中引入疲劳失效的模糊定义，考虑模糊不确定性的影响进行了疲劳失效概率计算[6]。崔磊等[7]研究了深水半潜式平台在我国南海12个区域的疲劳可靠性。Siddiqui与Suhail Ahmad[8]分别运用疲劳累计损伤与断裂力学方法分析了TLP平台系索连接处的疲劳寿命与疲劳可靠性，并分析了疲劳参数的敏感性。Kjerentroen等[9]将TLP作为串联系统，对张力筋腱进行了疲劳可靠性分析。Wirsching和Chen[10]总结了众多疲劳可靠性的研究，对如何在海洋结构物设计中有效使用疲劳可靠性方法进行了说明。Maria Celia C.Ximenes[11]对TLP平台张力筋腱节点的疲劳失效进行了调查，并考虑参数的不确定性进行了可靠性分析。

本文建立了张力腿平台(TLP)的有限元模型，计算了立柱与浮箱连接节点(NODE)结构关键连接位置在不同浪向和波浪圆频率下的应力传递函数。选用JONSWAP谱对波浪进行描述，结合南海某区域的波浪散布图，对NODE结构的疲劳筛选分别进行了确定性疲劳和疲劳可靠性计算，并对计算结果进行了对比分析。

1 确定性疲劳分析

船舶与海洋结构的确定性疲劳分析可采用谱分析方法。假设所分析的结构系统为线性系统，这样，从单位波高的计算结果能够推算各个波高的计算结果，并且应力的传递函数可以进行线性叠加。同时，还假设结构应力范围长期分布为分段连续，短期分布为窄带平稳随机过程，且服从瑞利(Rayleigh)分布。

在谱分析方法中，最关键的参数是应力幅值的传递函数Hσ(ω|θ)，即单位波幅导致的结构应力幅值。可通过有限元进行计算。

通过应力传递函数Hσ(ω|θ)和波浪散布图中某一个短期海况的波浪谱密度函数Sη(ω|Hs,Tz)，可由下式得到应力能量谱Sσ(ω|Hs,Tz,θ)

应力能量谱的第n阶谱矩mn为

由于短峰波引起的波浪能量分散可通过一个余弦函数kcosqα加以考虑，根据ITTC的推荐值，可取k=2/π，q=2。平方余弦函数假设的传播方向处于与选定波浪方向成-90°至+90°夹角的范围内，也即半个平面，如图1所示。考虑波浪扩散函数后的谱矩公式为

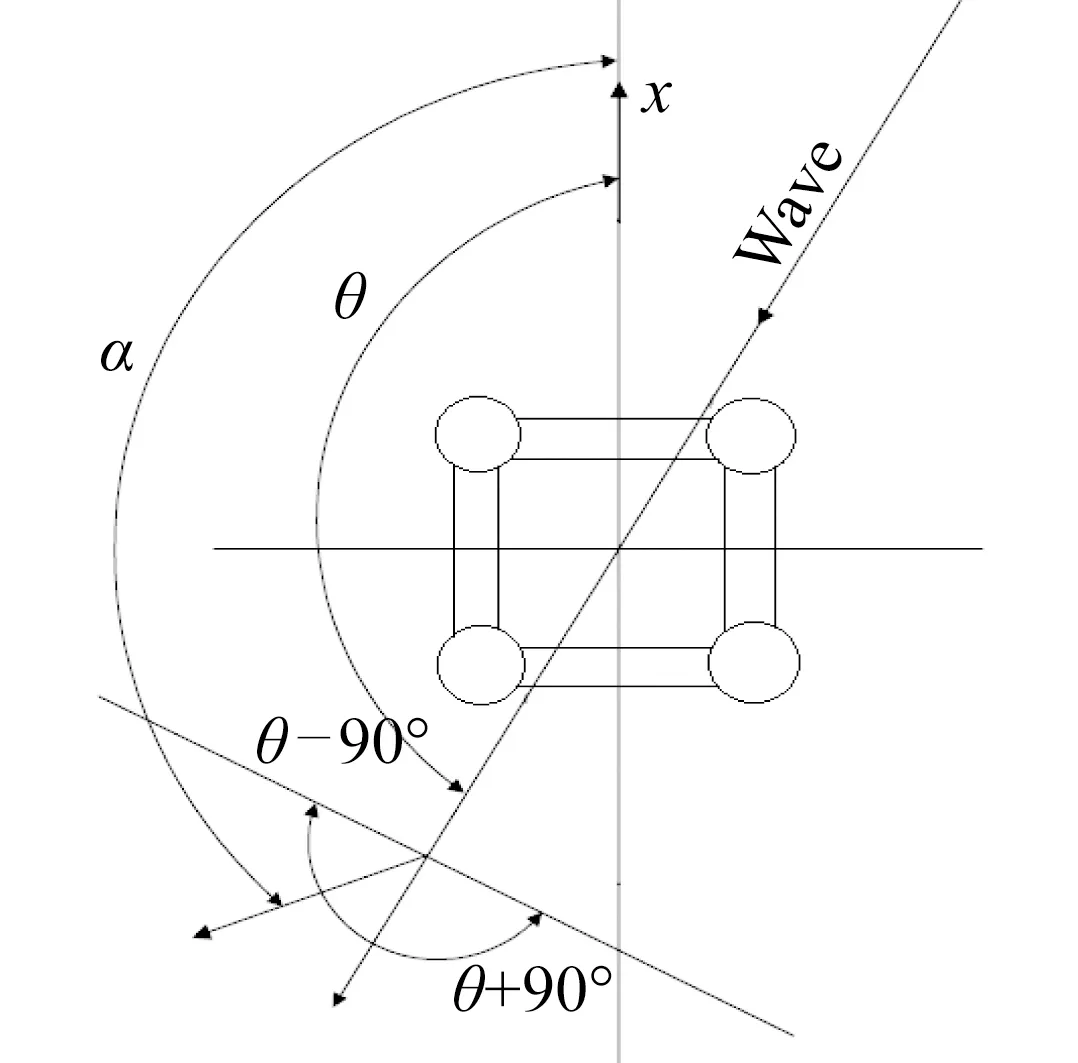
图1 波浪扩散角的定义Fig.1 Spreading angles definition

应用得到的谱矩，可以得出平均上过零频率

和谱宽参数

式中：m0、m2、m4为应力谱的零阶、二阶和四阶矩。

对单斜率S-N曲线，疲劳累积损伤可以采用如下闭式表达式计算：

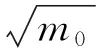
式中：a(m)=0.926-0.033m，b(m)=1.587m-2.323。

对于两段直线的S-N曲线，在拐点(Nq，Sq)处，该S-N双直线直线段的m变为r=m+Δm(Δm>0)，并且常数由K1变为K2。在这种情况下，式(6)中的疲劳损伤表示为

式中：μi为持续参数，值在0和1之间，用以计算落在S-N曲线中更低一段内的应力循环对疲劳损伤的贡献，μi的计算如下：

当应力范围分布的概率密度函数为瑞利分布时，μi为

2 疲劳可靠性分析

船舶与海洋工程结构疲劳可靠性分析就是在规定时间内，分析结构在已知波浪谱、长期应力范围分布函数、材料S-N曲线以及合适的参数概率分布等条件下不发生疲劳失效的概率，并称此概率为疲劳可靠度，用Pr表示。而结构发生疲劳破坏的概率定义为失效概率，用Pf表示。

当应力范围长期分布为分段连续，且每一个短期分布服从瑞利分布时，令应力参数为

则任意时间T内的累积损伤D可表示为

当结构发生疲劳失效时，由式(12)可得失效时的疲劳寿命为

式中：K为S-N曲线的参数，为一随机变量，反映疲劳强度的不确定性。Ω与应力范围概率和作用频率有关，反映了疲劳载荷的随机性。

另外，定义随机变量B以考虑疲劳载荷计算过程中的不确定性，包括在海况描述、波浪力计算、结构应力计算等方面采用的种种假设和理想化模型导致的计算误差。其次，由于Miner线性累积损伤的近似性，使得真实结构发生疲劳破坏时，累积损伤度并不总等于1，为计及这一不确定因素，用随机变量Δ来表示结构发生疲劳破坏时的累积损伤度。计及以上两个不确定因素，结构的疲劳寿命为

假设结构的设计寿命为TD，且K、B和Δ皆服从对数正态分布，则结构的疲劳可靠度为

定义安全裕量

由于Δ、B和K服从对数正态分布，则lnΔ、lnB和lnK服从正态分布，于是安全裕量为正态随机变量的线性函数，可靠性指标可表示为

式中：μlnΔ、μlnB和μlnK为lnΔ、lnB和lnK的均值，σlnΔ、σlnB和σlnK为lnΔ、lnB和lnK的标准差。

成矿母岩往往具有多期多相的复杂结构，一般岩石具有斑状结构。在产状较复杂的花岗岩中，常含有多层中粒及细粒斑状花岗岩，前者为第1期，后者为第2期。无论是第1期还是第2期，它们在成分上都有显著的差异变化，如第2期有细晶岩、花岗斑岩、微斜花岗岩、闪长玢岩以及煌斑岩岩脉。

于是，可靠性指标可表示为

3 某TLP平台NODE结构确定性疲劳与疲劳可靠性对比计算

3.1计算模型

采用ANSYS建立TLP的整体模型，其中，船体壳结构、隔离舱壁、立柱水平板以及立柱和浮筒的内部框架腹板都采用4节点shell63单元建立。所有加强筋以及框架面板都采用beam188模拟。采用mass21单元模拟下浮体和组块中的集中质量。组块结构采用beam188模拟整体框架。张力筋腱采用弹簧单元模拟。用于本文疲劳计算的NODE结构以及疲劳筛选的单元位置如图2所示。

3.2应力传递函数的计算

疲劳计算中波浪的圆频率范围取0.2～1.7 rad/s，间隔为0.05 rad/s。浪向角取0°至337.5°，间隔为22.5°。波高取2 m，即单位波幅。采用AQWA-LINE进行水动力计算，用ASAS获取船体外壳信息，然后采用AQWAWAVE将波浪信息以波浪外压和惯性力的形式映射到船体结构，并进行结构计算。将不同频率的单位波幅产生的各项载荷按实部和虚部处理，得到相应的实部应力σC(ω|θ)和虚部应力σS(ω|θ)，二者合成即得到应力幅值

则应力传递函数为

图3为Elem7的应力传递函数随波浪圆频率的变化曲线，为了便于观察，只选取部分浪向角传递函数进行展示。

图3 Elem7的应力传递函数曲线Fig.3 Curves of stress transfer function of Elem7

3.3确定性疲劳与疲劳可靠性对比计算及分析

本文计算选取TLP平台的设计寿命为20年，安全系数取10[12]，则许用疲劳寿命为200年。目前海工规范未对可靠性指标的目标值进行规定，但Kjerengtroen和Wirsching[9]、 Wirsching和Chen[10]、Maria,Celia C.Ximenses[11]、Stahl和 Geyer[13]等都对TLP的关键结构进行了疲劳可靠性的研究，对关键结构的疲劳可靠性指标β0皆取3.0进行评估。胡毓仁、李典庆和陈伯真[14]在其船舶与海洋工程疲劳可靠性分析的专著中也列出了TLP平台结构β0的取值，如表1所示。在本文的分析中，对于NODE结构连接关键位置，可靠性指标取3.0。

表1 TLP结构疲劳可靠性指标的取值Tab.1 Values of target safety index of TLP

在进行谱疲劳筛选计算时，S-N曲线选取非管节点在海水中带有阴极保护的F曲线[15]，并对应选取K的中值和变异系数。选取南海流花油田区域的波浪散布图，对短期海况采用JONSWAP描述，并假设应力范围的短期分布服从瑞利分布。Δ、B、K的中值及变异系数参考Wirsching等人[10-12]的论文选取，如表2所示。

表2 各随机变量的中值及变异系数Tab.2 Medians and COVs of variables

选取TLP平台NODE结构连接肘板端部和肘板中间位置的26个单元的单元面力得到应力传递函数，并进行疲劳计算和结果讨论。表3给出了不同单元的确定性疲劳以及疲劳可靠性的计算结果，为了便于观察，结果按照损伤大小排列。

表3 选取单元的累积损伤、疲劳寿命及可靠性指标Tab.3 Accumulative damage,fatigue life and reliability index of selected elements

选取疲劳累积损伤相对较大单元的疲劳寿命和对应的可靠性指标，见图4、图5，并在图中添加许用寿命和可靠性指标目标值作为参考。

图4 选取单元的疲劳寿命Fig.4 Fatigue life of selected elements

图5 选取单元的可靠性指标Fig.5 Reliability index of selected elements

由图4、图5可知，TLP平台NODE结构采用确定性疲劳和疲劳可靠性两种方法计算皆有局部位置不满足疲劳强度的要求。其中采用确定性疲劳方法有四个单元位置的疲劳寿命低于许用值，分别为图2中的Elem7、Elem8、Elem15、Elem24；而采用疲劳可靠性方法只有一个单元位置疲劳可靠性指标低于目标值，该单元为Elem7。针对疲劳筛选中不满足要求的单元位置，需要进行详细的疲劳分析。

另外，对比图4、图5可以发现，确定性疲劳方法计算的疲劳寿命和疲劳可靠性计算的可靠性指标随单元(即结构位置)变化的趋势是一致的。但是采用确定性疲劳方法检验疲劳强度时，有四个单元位置不满足要求；而采用疲劳可靠性方法时只有一个单元位置不满足要求。可见，相比于疲劳可靠性，确定性方法是更加保守的。

4 结 语

本文针对某TLP平台NODE结构，采用确定性疲劳和疲劳可靠性方法进行了疲劳筛选计算和对比，得出以下结论：

1) 采用两种疲劳计算方法得到的疲劳筛选结果皆表明该结构有局部位置不满足疲劳强度的要求，需要后续进行详细疲劳计算。不满足疲劳要求的位置主要在浮箱和立柱连接肘板的端部；

2) 两种方法的计算结果对于结构不同单元位置具有相同的变化趋势，但采用确定性疲劳方法校核疲劳强度时，不满足要求的单元位置更多，这说明确定性疲劳方法相比于疲劳可靠性方法更加保守。

可见，工程上常采用确定性的疲劳方法进行设计是更加安全的。但是如果能准确获得疲劳计算中各随机变量的分布和参数，采用疲劳可靠性方法进行疲劳设计会获得更好的经济效益。

[1] 王延平,张泗文,王志强,等.墨西哥湾“深水地平线”钻井平台事故分析与反思[J].事故分析与报道,2011,11(8): 5-8.(WANG Yanping,ZHANG Siwen,WANG Zhiqiang,et al.Analysis and reflection of deep horizon rig incident in Mexico Gulf[J].Safety Health & Environment,2011,11(8): 5-8.(in Chinese))

[2] TORGEIR Moan.The alexander L.Kielland accident[C]//The First Robert Bruce Wallance Lecture.Dept.of Ocean Engineering,Massachusetts Institute of Technology,April,1981.

[3] 刘刚,郑云龙,赵德有,等.BINGO9000 半潜式钻井平台疲劳强度分析[J].船舶力学,2002,6(24): 54-63.(LIU Gang,ZHENG Yunlong,ZHAO Deyou,et al.Fatigue strength analysis of BINGO9000 semisubmersible drilling rig[J].Journal of Ship Mechanics,2002,6(24): 54-63.(in Chinese))

[4] 张剑波.半潜式钻井船典型节点疲劳可靠性分析[J].船舶工程,2006,28(1): 36-40.(ZHANG Jianbo.Fatigue reliability analysis of typical joints in a semi-submersible drilling ship[J].Ship Engeering,2006,28(1): 36-40.(in Chinese))

[5] 陈伯真,胡毓仁.液化气体船液舱结构的疲劳可靠性分析[J].中国造船，1993,12(3): 67-78.(CHEN Bozhen,HU Yuren.Fatigue reliability analysis of tank structure in liquified gas garriers[J].Shipbuilding of China,1993,12(3): 67-78.(in Chinese))

[6] 胡毓仁,陈伯真.海洋结构管节点疲劳失效的模糊定义及可靠性分析[J].上海交通大学学报,1995,29(2): 21-25.(HU Yuren,CHEN Bozhen.Fuzzy definition of fatigue failure and reliability assessment for tubular joints of offshore structures[J].Journal of Shanghai Jiaotong University.1995,29(2): 21-25.(in Chinese))

[7] 崔磊,何勇,金伟良.不同海域Semi平台关键节点的疲劳可靠性分析[J].浙江大学学报,2013,47(8):1 329-1 337.(CUI Lei,HE Yong,JIN Weiliang.Fatigue reliability analysis on key nodes of a deepwater semi-submersible platform in different sea areas[J].Journal of Zhejiang University,2013,47(8):1 329- 1337.(in Chinese))

[8] N A Siddiqui,SUHAIL Ahmad.Fatigue and fracture reliability of TLP tethers under random loading [J].Marine Structures,2001,14(3): 331-352.

[9] KJERENGTROEN L,WIRSCHING P H.Structural reliability analysis fo series system[J].Journal of Structural Engineering,1984,110(7):1 495-1 511.

[10] P H Wirsching,Y N Chen.Considerations of probability-based fatigue design for marine structures[J].Marine Structural Reliability Symposium,The Ship Structure Committee and SNAME,Arlington VA,1987,Marine Structures,1988,(1):31-43.

[11] MARIA,CELIA C Ximenses.Fatigue reliability and inspection of TLP tendon system[J].Marine Technology,1991,28(2): 99-110.

[12] 中国船级社.海洋工程结构物疲劳强度评估指南[M].2013,39-40.(CCS.Guidelines for fatigue strength assessment of offshore engineering structures[M].2013,39-40.(in Chinses))

[13] STAHL B,GEYER J F.Ultimate strength reliability of tension leg platform tendon systems[C]//Offshore Technology Conference.OTC 4857,1985.

[14] 胡毓仁,李典庆,陈伯真.船舶与海洋工程结构疲劳可靠性分析[M].哈尔滨工程大学出版社,2009,125-146.(HU Yuren ,LI Dianqing,CHEN Bozhen.Fatigue reliability analysis of ship and offshore engineering structures[M].Harbin Engineering University Press,2009,125-146.(in Chinese))

[15] British Standards Institution.Code of practice for fixed offshore structures[S].BS6235,1982.

Comparison of ascertainable fatigue and fatigue reliability for TLP NODE structure

LIANG Yuanhua1,GAO Ming2,WEI Sijun2,YANG Qingxia1

(1.Ocean Engineering Technology Research and Development Center,China Classification Society,Beijing 100007,China; 2.Beijing Digital Easy Technology Development Co.,LTD,Beijing 100007,China)

Ascertainable fatigue is usually used in fatigue design in engineering for TLP.But most variables affecting fatigue life are random.The uncertainties of these variables can’t be described objectively in ascertainable fatigue method.So both the ascertainable fatigue and fatigue reliability methods are used in fatigue analysis for a TLP NODE structure based on spectral-based fatigue assessment in this paper.The results show that some local areas of the NODE are not of adequate size for fatigue screening strength.In addition,the ascertainable fatigue method is conservative compared to that of fatigue reliability.

TLP; ascertainable fatigue; fatigue reliability; spectral-based fatigue; fatigue life; reliability index

TG405

A

10.16483/j.issn.1005-9865.2017.05.014

1005-9865(2017)05-0118-07

2016-10-18

500米水深油田生产装备LTP自主研发专项经费资助。

梁园华(1976-)，男，江西宜春人，教授级高级工程师，主要从事海洋工程规范和科研工作。E-mail: yhliang@cce.org.cn