镁合金粘接层失效的非线性超声检测研究*

苏 珊

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

1001-2265(2017)10-0110-04

10.13462/j.cnki.mmtamt.2017.10.026

2016-12-22；

2017-02-20

河南省科技计划项目(152300410201)；河南省高等学校重点科研项目计划(13B430946)

苏珊(1977—)，女，河南太康人，河南理工大学副教授，硕士，研究方向为检测技术及应用，(E-mail)yanbingsheng@163.com。

镁合金粘接层失效的非线性超声检测研究*

苏 珊

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

粘接层脱粘问题直接影响材料或结构的整体性能，需要采用合适的方法尽早检测。针对此问题，提出利用非线性超声无损检测方法对其进行检测，建立了粘结层失效的非线性超声测试系统，对脱粘不同程度的镁合金粘结层试件进行了试验研究，有效测量了表征粘接层失效程度的超声非线性系数β，结果表明超声非线性系数对镁合金粘结层失效非常敏感，且随脱粘程度呈二次函数关系增加；同时，建立了有限元仿真模型，对脱粘不同程度的镁合金粘结层试件进行了有限元数值仿真，仿真结果和实验结果在变化趋势上近似一致，进一步证明非线性超声检测技术可以用于粘接层界面失效的无损评价。

非线性超声；粘接层失效；超声非线性系数

0 引言

粘接结构在航空、造船和汽车工业中广泛存在，但在热、撞击和交变载荷等外力作用下极易发生脱粘或疲劳开裂，从而造成严重的事故[1]，因此发展一种能够检测粘接层失效的无损检测方法对预测设备的故障从而避免重大损失具有重要意义。

常规超声回波法可以对粘接层中的孔洞、裂缝以及脱胶等较大缺陷进行检测[2-3]，但是对粘接层失效面积较小时的性能退化以及微小裂纹的检测效果不佳。近期的研究结果表明超声波在粘接界面中传播时会使粘接层中的微小缺陷发生拍打效应，超声波波形也会随之畸变，从而产生高次谐波，粘接层失效程度与高次谐波幅值之间具有定量的关系[4]。目前已有Idjimarene等人的研究表明非线性超声可以用来检测固体材料中的微小缺陷[5-7]。但是将非线性超声用于镁合金粘接结构早期失效检测的研究较少，而镁合金具有密度小、强度和刚性高等优点，被广泛用于各种制造业的粘接结构中[8]，对其进行早期失效检测研究对于保障设备安全运行有重大意义。

本文以AZ31镁合金作为对象，通过有限元仿真和试验的方法对 AZ31 镁合金粘接层失效进行了非线性超声无损检测研究。

1 超声非线性系数

固体介质的非线性主要有经典非线性和接触非线性,粘接层失效属于接触非线性[8]。根据Breazeal等[9]建立的一维纵波非线性波动方程,可以得到表征材料损伤程度的非线性系数为：

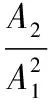
(1)

方程中，A1和A2分别为基波和二次谐波幅值，k为波数，主要与声波频率有关。x为波传播距离[10]。β可以作为描述粘接界面局部缺陷的量化指标。

2 有限元仿真

2.1 模型

粘接层厚度相对于其他特征尺寸而言较小，一般在几十μm到几百μm之间，粘接层脱粘属于微缺陷。根据非线性超声检测原理，建立相应FEM模型如图1所示。

图1 FEM模型

为了减小计算量，采用有限元二维平面单元和轴对称模型，镁合金粘接结构试件简化为长26mm，厚10mm的二维平面，粘接层厚0.32mm，脱粘造成的面缺陷转化为椭圆形线缺陷。在二维平面里，纵波沿试件表面垂直于粘接层传播至另一面。在试件的粘结层中间位置，预设1个长0～5mm，宽0.3mm的椭圆形微缺陷。超声波将与微缺陷发生非线性相互作用，从而产生二次谐波。

试验材料为AZ31镁合金，弹性模量E=46GPa，泊松比ν=0.272，密度为1770kg/m3，屈服极限199MPa，强度极限259MPa，纵波波速为5710m/s；粘合剂为AF-163-2K材料，密度为1.124 kg/m3，弹性模量E=1.1GPa，泊松比为0.34。发射信号频率为5MHz，幅值为60μm。为了避免波形重叠，发射信号取10个周期。

2.2 计算结果

图2分别为设有3mm缺陷时接收到的频域信号。从图中可以看出，5MHz处为基波，10MHz处为二次谐波。

图2 有缺陷时接收到的频域信号

图3为脱粘长度的变化与超声非线性系数的关系曲线。从图中可以看出，当脱粘长度从2.2mm增长到5mm的过程中，超声非线性系数与脱粘长度呈二次函数关系增加。有限元仿真结果表明，超声非线性系数对粘接层脱粘产生的微缺陷长度变化非常敏感，有限元方法可以有效的模拟粘接层失效的非线性超声波检测，模拟结果可以为试验研究提供参考。

图3 超声非线性系数与脱粘长度的关系曲线

3 试验系统与测量方法

3.1 镁合金粘接界面试件

两侧被粘接物材料为AZ31镁合金，其厚度为10mm，直径为26mm；粘合剂为AF-163-2K材料，厚度为0.32mm。

如图4所示，试件表面被均分12份，分别涂抹不同份数的粘接剂，试件被分为完全不脱沾、脱粘1/12、2/12到完全脱粘共13种情况。

图4 粘接层试件示意图

3.2 测试系统

图5所示为粘接层失效超声非线性系数测量试验系统框图，采用美国RETIC公司的非线性超声检测系统。主机箱中的信号发生器产生5MHz的10个周期单一频率超声脉冲串，经由功率放大器放大、高能低通滤波器滤除高频干扰后，由发射探头耦合入镁合金脱粘试件，接收探头接收传过来的声波经由高通滤波器和放大器送入示波器显示并送入计算机进行傅里叶变换，获取基波和二次谐波幅值。

图5 粘接层检测试验系统示意图

图6为发射和接收窄带PZT探头，中心频率分别为发射5MHz，接收10MHz。耦合剂为更加稳定的锂基黄油。

图6 实验所用PZT探头

如图7所示，一个特殊的夹具来保证试验的可重复性。图中的微型压力计可以测量探头与试件之间的压力，可以保证每次的实验条件尽量一致。

图7 试验夹具图

3.3 试验信号

图8所示为接收信号时域波形，可以看出，波形脱粘的粘接层后出现了明显的扭曲变形。利用积分门框选一次透射波并进行傅里叶变换，得到图9所示的频域波形。

图8 接收信号时域波形

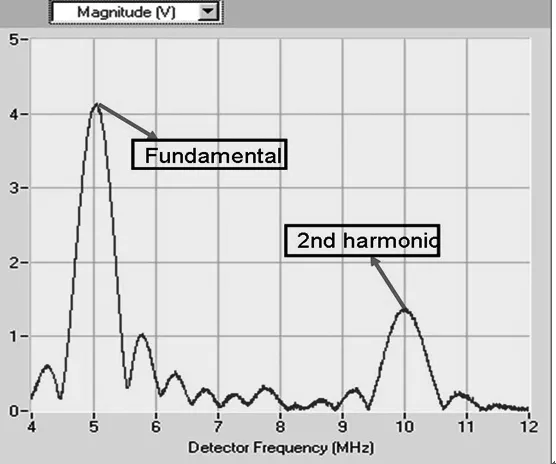
图9 接收信号频域波形

从图中可以看出，除了频率为5MHz处的基波外，10MHz处有明显的二次谐波。测量基波幅值A1和二次谐波的幅值A2，代入方程(1)就可获得超声非线性系数。

4 试验结果与分析

4.1 测试方法与试验结果

将试件安装在图7所示的夹具中，首先测量未脱粘时的基波和二次谐波幅值，然后依次测量脱粘面积为1/12、2/12，直到完全脱粘试件的基波和二次谐波幅值。图10所示为不同脱粘程度的基波和二次谐波幅值。

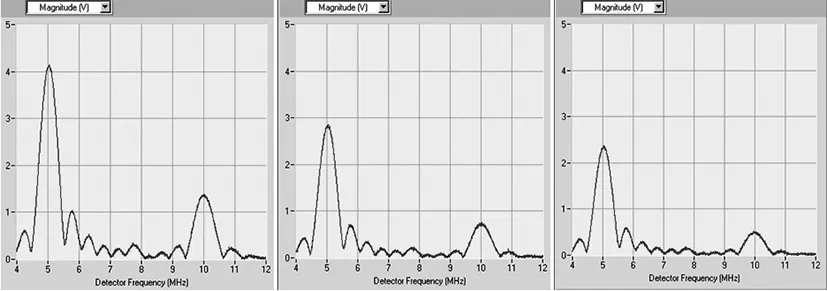
(a) 无脱粘 (b) 脱粘11/12 (c) 脱粘10/12

(d) 脱粘9/12 (e) 脱粘8/12 (f) 脱粘7/12

(g) 脱粘6/12 (h) 脱粘5/12 (i) 脱粘4/12

(j) 脱粘3/12 (k) 脱粘2/12 (l) 脱粘1/12

(m) 全脱粘图10 不同脱粘程度的基波和二次谐波幅值

通过公式(1)分别计算不同脱粘程度的相对超声非线性系数。图11为相对超声非线性系数随脱粘程度的变化曲线。

图11 相对超声非线性系数随脱粘程度的变化曲线

4.2 测试结果分析

从图11可以看出，随着脱粘程度的增加，相对超声非线性系数近似按二次函数规律增加，特别是在脱粘面积占总面积的一半之前的早期性能退化阶段，曲线更平滑。试验结果与有限元仿真结果基本吻合。结果表明，超声非线性系数可以很好的表征粘接层失效程度，非线性检测方法可以用于镁合金材料的脱粘程度检测。

通过试验结果和仿真结果的比较，可以看出，两者超声非线性系数与脱粘程度关系的变化趋势近似一致，均为二次函数关系。相比于有限元仿真结果，试验结果的数值较为分散，这主要是由于实际测量中试验系统对试验结果有一定的影响，虽然通过优化夹具来保证试验条件的一致性，但也不能做到像仿真环境一样理想。另外，试验系统中采取了滤波、加窗、放大和谐波抽取等信号处理环节，所以试验结果和仿真结果在幅值上不具有可比性。

从图11中可以看出，试件没有脱粘时超声非线性并不为零，这有两方面的原因，一方面任何金属材料本身存在由于晶格非谐和引起的固有非线性；另一方面试验系统也存在一定的非线性干扰。

5 结论

针对镁合金粘接层失效问题，建立了镁合金粘接界面脱粘的非线性超声测试系统，对粘接界面脱粘试件进行了非线性超声无损检测试验研究。同时建立了粘接界面脱粘的非线性超声检测有限元模型。获得了如下结论：

(1)试验结果表明，随着脱粘程度的增加，相对超声非线性系数近似按二次函数规律增加，非线性超声信号对脱粘非常敏感。另外超声非线性粘接界面有脱粘情况时比无脱粘时的超声非线性系数大的多也说明试验系统是可靠的。

(2)仿真结果表明，超声非线性系数随粘接界面失效程度增加而增加。有限元仿真结果与试验结果在变化趋势上近似一致，进一步证明了非线性超声检测技术可以用于粘接层界面失效的无损评价。

[1] BI Zhouyang, CHEN Jianhui, WANG Guanglong, et al. Nonlinear ultrasonic detection of kissing bonds in adhesive interface[J]. Journal of PLA university of science and technology,2015,16(1):62-67.

[2] 张毕强, 秦训鹏, 方洲, 等. 汽车发动机缸体自动化无损检测系统研究[J].组合机床与自动化加工技术,2015 (7):106-109.

[3] 焦圣喜, 魏宏建. 一种工业无损检测超声图像降噪方法[J]. 组合机床与自动化加工技术,2013 (9):70-72.

[4] A Novak, M Bentahar, V Tournat, et al. Nonlinear acoustic characterization of micro- damaged materials through higher harmonic resonance analysis[J]. NDT&E International, 2012, 45(3): 1-8.

[5] S Idjimarene, M Bentahar. Effects of experimental configuration on the detection threshold of hysteretic elastic nonlinearity[J]. Ultrasonic, 2014, 54(7): 1861-1867.

[6] K Y Sohn, J W Jones, J Berkmortel, et al. Creep and Bolt Load Retention Behavior of Die Cast Magnesium Alloys for High Temperature Application[J]. SAE Technical Paper Series, 20002-012-1120, Warrendale, PA, 2000.

[7] AN Zhiwu, WANG Xiaomin,LI Mingxuan,et al. Theoretical development of nonlinear spring models for the second harmonics on an interface between two solids[J]. Chin. Phys. Lett., 2009,26(11): 118-121.

[8] ZHOU Zhenggan, LIU Siming. Nonlinear ultrasonic techniques used in nondestructive testing: A review[J]. Journal of Mechanical Engineering, 2011, 47(8): 2-11.

[9] M A Breazeale, Jacob Philip. Determination of Third order Elastic Constants from Ultrasonic Harmonic Generation Measurements[C]. Physical Acoustics, Vol. 17, Academic Press, INC.,1984.

[10] YAN Bingsheng, LIU Ziran, ZHANG Yuechun, et al. Experimental Study of Early Fatigue Nonlinear Ultrasonic Detection in Magnesium Alloy, 2013, 49(4): 20-24.

StudyofaNon-linearUltrasonicforDetectingtheDebondingoftheAdhesiveLayersofMagnesiumAlloys

SU Shan

(School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo Henan 454000,China)

A non-linear ultrasonic system for testing the debonding of the adhesive layers which is expected to influence the overall performance of materials or structures was established. On which this non-linear ultrasonic non-destructive testing method was used to test specimens thereof on magnesium alloys with different degrees of debonding. By doing so, the ultrasonic non-linearity parameterβwas measured effectively. The experimental results demonstrated that the ultrasonic non-linearity parameter was sensitive to the debonding of the adhesive layers of the magnesium alloys, and exhibited a quadratic relationship with the degree of debonding as the latter increases. Besides, a finite element simulation model was established to perform numerical simulation of the specimens of the adhesive layers of magnesium alloys which had debonded to different degrees. The simulation and experimental results had a same change tendency, which further demonstrated that the proposed non-linear ultrasonic testing technology is applicable to the non-destructive evaluation of the debonding of the adhesive layers.

non-linear ultrasonics, debonding adhesive layer;ultrasonic non-linearity parameter

TH142;TG506

A

(编辑李秀敏)