基于滑模变结构控制的鲁棒控制器设计
刘大伟
(南京工程学院 自动化学院 ,南京 211167)
1001-2265(2017)10-0105-05
10.13462/j.cnki.mmtamt.2017.10.025
2016-12-10;
2017-01-12
刘大伟(1980—),男,安徽萧县人,南京工程学院实验师,硕士,研究方向为电机控制算法,(E-mail)zdhxldw@njit.edu.cn。
基于滑模变结构控制的鲁棒控制器设计
刘大伟
(南京工程学院 自动化学院 ,南京 211167)
为了有效抑制状态变量的超调,加快转子的收敛速度,增强系统的抗干扰性,提出了一种基于滑模变结构控制方法的鲁棒控制器。与传统PID控制器不同,该控制器采取最终滑动模态的极点配置方式对系统的期望闭环动态以及选择滑模面进行设计,然后采取基于李亚普诺夫稳定性理论的控制方法来设计滑模控制器,使系统在设计的滑模面上具有期望闭环动态,在执行器动态变化导致误差的情况下,所述系统依旧可以在有限时间内收敛到设计的滑模面。该控制可以代替PID控制器应用于永磁同步直线电机,验证所设计的控制器在系统参数(动子质量、粘滞摩擦系数)发生较大变化和负载扰动情况下,都保持良好的跟踪性能,实现系统对不确定性扰动下的强鲁棒性。
永磁同步直线电机;鲁棒控制器;滑模变结构控制
0 引言
永磁同步电机(PMSM)以其高转矩、高功率、高效率等优异的性能,在数控机床、工业机器人以及航空航天等领域得到了广泛的应用[1]。但PMSM是一个多输入、非线性、强耦合、变参数的较为复杂对象。虽然在一定程度上传统的PID控制可以满足控制要求,但PID控制需要精度较高的数学模型,比较容易受到外部扰动与系统内部参数变化的影响,鲁棒性 不强,不能满足一些高性能的要求。最近几年,许多研究学者对控制器的研究开始转向现代控制理论中的自适应控制、模糊控制、神经网络控制等,这些先进的控制器虽在一定程度上改善了系统的性能,但仍存在诸多缺点。比如文献[2]提出将模糊控制引入到控制系统中,由于模糊论域固定,模糊控制器稳态时依然存在较大的稳态误差,导致系统的精度受到了一定的影响;文献[3]提出的神经网络控制理论虽然可以处理那些难以用模型或规则描述的过程或系统,但需要进行自适应学习,系统参数的调整需要对数据进行长时间的处理,导致开发系统的成本增加;文献[4]提出的自适应控制对系统未知的变化可以自动地使系统时刻处于希望状态。
滑模变结构控制理论是一种非线性的控制理论,以其对系统建模精度要求低,对系统参数变化与外部扰动具有很强的鲁棒性,因此,在高性能、高精度的永磁同步电机(PMSM)控制系统中得到了广泛应用。
本文提出了一种基于滑模变结构控制方法的鲁棒控制器取代传统的PID控制器,并将其应用于永磁同步电动机的控制系统中,通过与传统PID控制器的性能对比,验证本文设计的控制器在系统参数发生变化和外部扰动情况下,该控制器依旧可以有效地提高系统的跟随性与鲁棒性。
1 建立永磁同步直线电机数学模型
为了获得永磁同步直线电机的高性能控制,首先需要对电机进行坐标解耦变换,本文采用id=0的控制方法。
根据直线电机的数学模型可得到PMLSM的电压及磁链方程:
ud=Rsid+pΨd-ωΨq
uq=Rsiq+pΨq+ωΨd
Ψd=Ldid+ΨPM
Ψq=Lqiq
(1)

由式(1)可以进一步得到,直轴电压平衡方程:

(2)
交轴电压平衡方程:
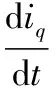
(3)
电机的总功率:

(4)

(5)
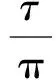

(6)
电枢中认为d-q轴电感相同,即Ld=Lq,因此:

(7)
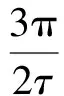
可得直线电机的电压方程、电磁转矩方程和运动方程分别为:
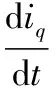
(8)
根据上述表达式,永磁同步直线电机的电磁推力仅与电枢交轴电流的幅值大小相关,完成解耦控制。因此,对永磁同步直线电机采用矢量控制可以使其工作在最佳运行状态。本文对永磁同步直线电机使用id=0控制策略,实现对电压分量ud的控制。则永磁同步直线电机的电压平衡方程、电磁转矩方程和运动方程为[5]:
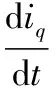
(9)
式中,M为动子质量,v为动子线速度,B为粘滞摩擦系数,Fm为电磁推力,Fd为负载阻力。
2 滑模变结构控制设计方法
与传统控制不同的是滑模变结构在于控制的不连续性,即使系统“结构”动态变化的开关特性[6]。
该控制法主要确保在状态空间内预先设计一个超平面,利用滑模变结构控制的不连续性,对系统结构作不断的变化,即在限定的条件下按照预定的状态轨迹进行小幅度、高频率的上下连续不断地运动,确保系统的状态沿着这个特殊的超平面逐渐滑向平衡点,最终在平衡点或者是平衡点附近的临界域内,即滑动模态运动。
考虑一般的情况,在系统的状态空间中,有一个超平面s(x)=0,如图1所示,它将整个状态空间分成σ>0和σ<0两部分。在超平面上的运动点可分成如下三种情况[7]:
(10)
(1) 普通点——由系统运动点运动到超平面σ=0附近时,穿过超平面,如图1上的A点;
(2) 初始点——由系统运动点运动到超平面σ=0附近时,向超平面的两边运动,如图1上的B点;
(3) 截止点——由系统运动点运动到超平面σ=0附近时,从超平面两边趋向该点运动,如图1上的C点。

图1 滑模面上的三种点的特性
滑模变结构控制中相对普通点与初始点,截止点具有特定含义,假如在某个切平面上的区域内全部点都是截止点,一旦系统运动状态渐进这个区域时,江北“吸入”在该区域内进行运动。所以称切换面σ=0上含有所有的截止点的区域为“滑模区”。在此区域内系统所做的运动称为“滑模运动”。滑模变结构控制主要是通过控制控制目标设计滑模切换面σ=0,迫使系统的状态点运动到滑膜切换面,在切换面上进行滑模运动,最终实现控制目的。
目前对滑模变结构控制的定义主要为:
设有一非线性系统:
(11)
确定切换函数矢量:
s=s(x),s∈Rm
(12)
寻求一种变结构控制函数:
(13)
(1) 滑动模态的存在条件;
(2) 滑动模态可达性条件;
(3) 确保滑模运动运行稳定,动态品质较好。
由式(12)、式(13)所描述且满足(1)~(3)的系统称之为变结构控制系统。因系统具有滑动模态,又可称为滑动模态控制。
对于多变量线性系统:

(14)
设计变结构滑模控制就是:
(1)选择切换函数s(x),即求矩阵C;
(2)确定变结构控制u(x),使得闭环系统中:
1)存在滑动模态;
2)所有的相轨线能够在有限时间内到达s0;
3)s0上的滑动模态不断趋近稳定,同时动态品质较好。对于线性系统滑模控制设计主要分为两步完成:设计滑移面与设计滑动模态控制器。
设计滑移面即确定切换函数s(x)=Cx中的矩阵C,给定s0=KerC以获得最终滑动模态的稳定性及品质。本文采用最终滑动模态的极点配置方法[8]。
在变结构控制系统状态进入滑动超平面σ=0时,滑动运动条件可写为:
(15)
则滑动模态运动方程为:
(16)
或写为:
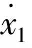
(17)
式中,ueq为滑动模态运动时的等价控制。
上式描述的系统标称方程为:
(18)
可得:
(19)
滑动模态控制系统设计的下一步主要是对控制器的设计,确保系统状态从切换超平面(即滑动模态)之外向切换超平面逐渐靠拢,最终停留在此超平面上。对于变结构滑模控制器的设计本文采用基于李亚普诺夫稳定性理论的控制[9]。
研究单输入系统:
(20)
选取控制:
u=-(BTV1B)-1[ksgn(BTV1X)+f(S)+BTV1AX]
(21)
其中,k>0,S=BTV1X,BTV1B≠0;
令η=(BTV1B)-1,其中V1为待定的对称矩阵,f(0)=0,Sf(S)>0。
选取李亚普诺夫函数为V=XTV1X,在控制u下,对V求沿着系统(20)关于时间t的导数:
对照组采用甲磺酸α-二氢麦角隐亭(由意大利多帕药业有限公司生产,注册证号H20091125)治疗,每次使用5mg,qd,在餐中口服,使用3-5d后无明显不良反应增加5mg,使用3-6个月。

(22)

总之,对任意给定的正定矩阵Q,可以得到另一正定矩阵D,并从D=V1-ηV1BBTV1中解出V1,V1也必是正定的。这样就确定了控制使得系统:
u=-(BTV1B)-1[ksgn(BTV1X)+f(S)+BTV1AX]
(23)
1) 切换面S(X)=BTV1X=0作为滑动模态区;
3) 系统是全局渐近稳定的。
3 永磁同步直线电机滑模变结构控制方法
永磁同步直线电机的运动方程可以写为:
(24)


(25)


(26)
写成矩阵形式可以表示为:
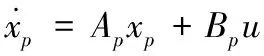
(27)
其中:
根据永磁同步直线电机的运动方程式(24)可以得到式(27)的状态空间形式:
(28)
根据滑模变结构控制设计方法,设期望极点λ<0,则假设x2=λx1,选择滑模面:
s=x2-λx1
(29)
求滑模面的V函数:
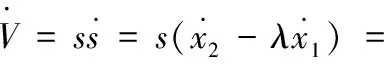
(30)
则由以上可知,选择控制:

(31)
4 基于滑模变结构控制方法的仿真与分析
4.1 滑模变结构控制的鲁棒控制器性能分析
直线电机的参数为:动子质量Mc=3.2kg,电机基座质量Mu=16.4kg,粘滞摩擦系数B=13.3Ns/m,推力系数Kf=21.78N/A,动子电枢电阻R=10.2Ω,动子电枢电感L=2.63mH,δ=0.001,ε=0.01。
控制器的期望输出由参考模型来设定,考虑到伺服控制特点,设定如下的跟踪特性[11]:
①无超调;
②无稳态误差;
③上升时间tc=0.1s。
满足上述性能的传递函数类型很多,为便于实现,选择二阶临界阻尼系统:
(32)
作为参考模型,其阶跃响应为:
y(t)=1-(1+μt)e-μt
(33)
系统满足无超调且稳态误差为零的特性,根据tc定义:
0.9=1-(1+μtc)e-μtc
(34)
得到μ=38.9,即am=77.8,bm=1513.21。
在系统参数变化的情况下,验证滑模变结构控制法对跟踪精度以及干扰的抑制能力,下面将对以下几种情况进行分析:①质量变化;②粘滞摩擦系数变化;③负载阻力变化。
①动子质量变化
当质量分别为Mc=1.5M0,Mc=2M0,Mc=4M0时,基于滑模变结构方法的控制器阶跃响应如图2所示。动子质量增大将会使系统的动态响应速度变慢,将会出现系统运行不稳定,产生爬升现象;相反,动子质量减小,系统动态响应速度变快,将会出现速度超调或是震荡现象。依据动子质量对控制器各参数进行整定,从图2可以看出,在较短时问内系统达到稳定,并未出现超调,而且轨迹几乎没有改变,可以认为系统在动子质量发生较大变化的情况下,满足设计要求,对动子质量变换具有较好的鲁棒性。

图2 质量变化时的滑模变结构控制器位置响应
②滞摩擦系数变化
当粘滞摩擦系数分别为B=1.5B0,B=2B0时,采用滑模变结构控制器,系统阶跃响应如图3所示粘滞摩擦系数的过大或是较小同样会对系统的响应时间、超调、稳定等产生影响,从图3可以看出,即使粘滞摩擦系数发生较大变化,如B=2B0时,系统的上升时间也仅为0.1001s,相对误差为0.1%,系统跟随特性与响应时间在没有变化的同时,对粘滞摩擦系数变化也保持了良好的鲁棒性。
③载阻力变化
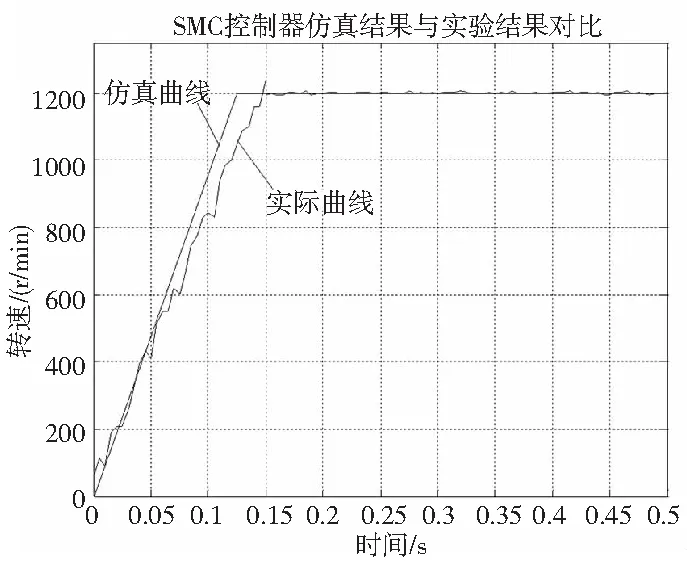
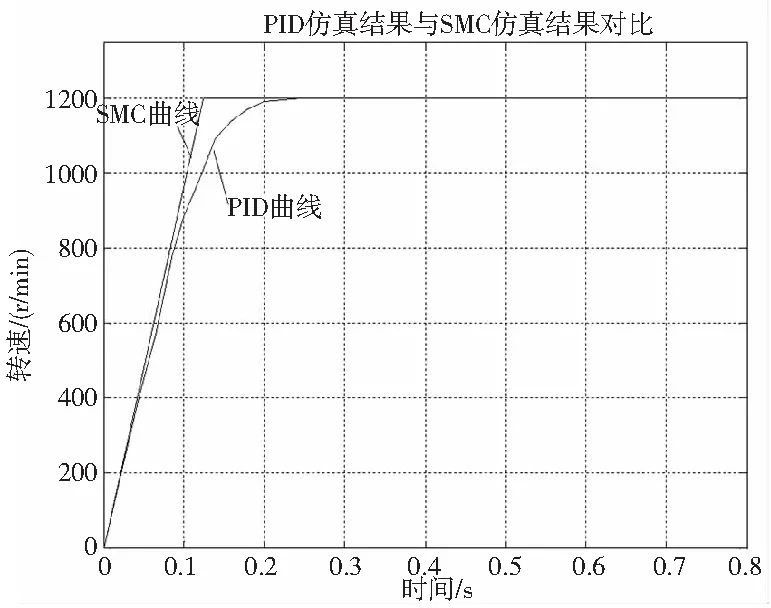
考虑负载阻力Fd,在标称模型状态下施加Fd=20N (5s 图4 考虑负载阻力情况下滑模变结构控制器位置响应 4.2 仿真结果分析 为了验证基于滑模变结构控制的鲁棒控制器对永磁同步电机PMSM控制系统的有效性,对本文提出的算法与传统PID控制器进行对比仿真和实验研究,在Matlab/SIMULINK环境下,电机选用TI公司的DSP中TMS320F2812芯片作为实验平台,仿真与实验设定的PMSM参数如表1所示。 表1 电动机参数 当电机启动,给定转速1200r/min。图5~图7为在传统PID控制器和本文设计控制器下的永磁同步电机空载启动时动态特性曲线对比图。 图5 PID控制器仿真结果与实验结果对比 图6 SMC控制器仿真结果与实验结果对比 图7 PID仿真结果与SMC仿真结果对比 从图中波形可以看出图5~图7中实际电机的转速值稍微偏小于仿真值,产生此情况的主要原因是系统变化量的动态过程,参数无法像仿真中发生突变。由图5和图6看出使电机达到设定的速度值,传统PID控制大约需要0.3s,而滑模变结构控制不到0.2s。从图7可以得出滑模变结构的响应时间比传统PID控制响应时间提高了将近1倍。所以可以看出基于滑模变结构控制的鲁棒控制器比传统PID控制器响应时间更快、没有超调、鲁棒性较强。 电机运行稳定之后,在PID控制下在0.6s时将负载由5N增加到10N,同样,在滑模变结构控制方式下,也在0.6s给控制系统添加扰动。如图8所示,在传统PID控制下系统转速波形图有明显的波动,外界对其施加扰动时,系统恢复需要较长时间进行调节,同时伴有稳态误差;但使用滑模变结构控制的鲁棒控制器控制系统时,系统转速表现出较好的动态特性,稳定运行,抗干扰强,鲁棒性好。 图8 PID仿真结果与SMC仿真结果结果对比 本文以永磁同步直线电机控制系统为平台,对转子质量、粘滞摩擦系数以及负载转矩变化对电机性能的影响进行分析,提出了一种基于滑模变结构控制方法的鲁棒控制器。通过系统仿真证明了本文设计的控制器具良好的跟踪性能,消除了原有系统超调现象,实现系统对不确定性扰动下的强鲁棒性,证明了理论分析的正确性。 [1] 童力,邹旭东,丰树帅,等.基于预测无差拍算法的永磁同步电机无传感器控制[J].电工技术学报,2013,28(3):17-26. [2] CHEN J Y. Expert SMC-base fuzzy control with genetic genetic algorithms [J].Journal of the Franklin lnstitute,1999,336 (4):589-610. [3] 卢达,赵光宙,曲轶龙,等.永磁同步电机无参数整定自抗扰 控制器[J].电工技术学报,2013,28 (3):27-34. [4] 李永坚,许志伟,彭晓.SRM积分滑模变结构与神经网络补偿控制[J].电机与控制学报,2011,15(1):33-37,43. [5] 余凤豪,吕飞,张松涛,等.永磁同步直线电机的数学模型分析[J].舰船电子工程,2010(9):120-122. [6] 贾洪平,贺益康.永磁同步电机滑模变结构直接转矩控制[J].电工技术学报,2006,21(1):1-6. [7] 唐勇奇,汪超,赵葵银.模糊滑模变结构控制在交流伺服系统中应用[J].微特电机,2006(2):36-38. [8] 姜静,伍清河.模糊滑模变结构控制技术的应用研究[J].电光与控制,2006,13(2):41-44. [9] 唐勇奇,汪超,沈学军.基于滑模变结构控制的变频调速系统[J].电气应用,2006,25(3):39-41. [10] Habetler T G,Profumo F,Pastorelli M,et al. Direct torque control of induction motor machines using space vector modulation[J]. IEEE Trans. on Industry Applications, 1992, 28:1045-1053. [11] Takahashi L, Noguehi T. A new quick-response and high-efficiency control strategy of an induction motor[J]. IEEE Trans. on Industry Application, 1986, 22(5):820-827. DesignofRobustControllerBasedonSlidingModeVariableStructureControl LIU Da-wei In order to effectively restrain the overshoot of the state variables, the convergence speed of the rotor is accelerated, and the anti-interference ability of the system is enhanced,put forward a method of variable structure control based on sliding mode robust controller. Different from traditional PID controller, the pole assignment controller to take the terminal sliding mode of the system and choose the desired closed-loop dynamic sliding mode surface is designed, and then take control method based on Lyapunov stability theory to design the sliding mode controller, the system in the design of the sliding surface is expected in the closed-loop dynamics, actuator dynamic changes lead to error, the the system can still converge in finite time to design the sliding surface. The controller can be used instead of PID controller for permanent magnet synchronous linear motor, validate the design of controller parameters of the system (the mover mass, viscous friction coefficient) change and load disturbance situation, maintain a good tracking performance and strong robustness to uncertainty under disturbances. permanent magnet linear synchronous motor;robust controller;sliding mode variable structure control TH122;TG659 A (编辑李秀敏)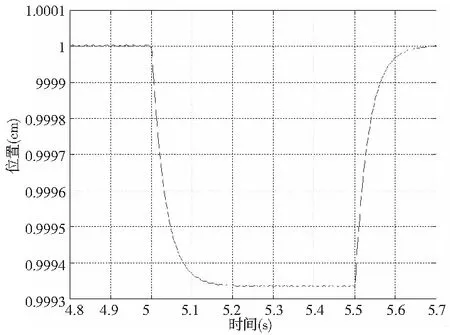



5 结论
(College of Automation,Nanjing Institute of Technology ,Nanjing 211167,China)

