谱消去粘性谱元方法求解对流扩散方程
时永兴
(华电江苏能源有限公司句容发电厂,江苏 镇江 212400)
谱消去粘性谱元方法求解对流扩散方程
时永兴
(华电江苏能源有限公司句容发电厂,江苏 镇江 212400)
针对谱元方法求解高雷诺数下对流扩散方程的稳定性问题,采用Chebyshev谱元方法结合谱消去粘性法求解一维对流扩散方程。利用特征分析法预测了数值方法的求解稳定性,通过数值算例验证了该解法的可行性,讨论了谱消去粘性参数对求解稳定性及数值精度的影响。结果表明:和谱元方法相比,谱消去粘性谱元方法求解对流扩散方程的稳定区域有了明显的扩大,在高雷诺数时能够获得具有较高精度的数值解;较大的谱消去粘性项有利于稳定区域的扩大,而在计算稳定的条件下较小的粘性项有利于数值精度的提高,所以适当地设置粘性项的大小,在保证计算稳定的同时提高数值精度。
对流扩散方程;谱元法;谱消去粘性法;稳定性;高雷诺数
0 引言
对流扩散方程一般用来描述浓度、温度、涡量等物理量的转移扩散过程,在环境、化工、气象、水利等多个工程领域中都有着广泛的应用,因其重要性而备受关注。由于一般情况下难以求得解析解,高精度的数值解对于准确地理解物理过程中的对流扩散现象就有着重要的意义。
谱元方法[1]SEM (spectral element method)作为一种灵活的高精度数值方法,结合了谱方法的高精度和有限元法的复杂区域处理能力,非常适宜应用于对流扩散方程的数值求解。但当方程中含有很高的雷诺数Re时,应用谱元方法进行求解会出现传统的有限差分法[2]、有限元法[3]、谱方法[4]所遇到的稳定性问题,即对于一定的时间步长和网格划分存在Re数区间,只有当计算位于该Re数区间时,求解才是稳定的。因此,扩大稳定区域的范围成为谱元方法求解对流扩散方程的关键问题。
谱消去粘性法SVV(spectral vanishing viscosity)是由Tadmar[5]在利用Fourier谱方法求解双曲型守恒方程时首先提出的,Maday[6]等将其扩展到求解非周期问题的Legendre谱方法获得了守恒方程稳定的数值解;Heinrichs[7]利用谱消去粘性谱方法求解了含有边界层的稳态对流扩散方程,消除了边界层所造成的数值振荡;Karamanos和Karniadakis[8]首次将谱消去粘性法和谱元方法相结合,成功地计算了管道湍流;Xu和Pasquetti[9]将谱消去粘性法应用于配置点谱元方法,推广了其求解高维复杂区域问题的形式,并获得了高Re数下圆柱绕流的稳定数值解;Kirby和Sherwin[10]利用矩阵形式分析了谱消去粘性法和谱元方法的结合方式,对三维三角形管道湍流进行了求解。
本文在前期谱消去粘性谱元法研究的基础上,采用矩阵分析法提出求解过程的稳定性条件,系统地研究谱消去粘性谱元法求解对流扩散方程的稳定性问题及其扩大稳定域的效果。讨论谱消去粘性参数对稳定性和计算精度的影响,通过数值算例对谱消去粘性谱元法求解高Re数下对流扩散方程的有效性进行验证。
1 谱消去粘性法
谱消去粘性法求解对流扩散方程时,在方程中加入人工粘性项,稳定化的一维对流扩散方程形式为:
0
(1)
相应的初始条件和边界条件:
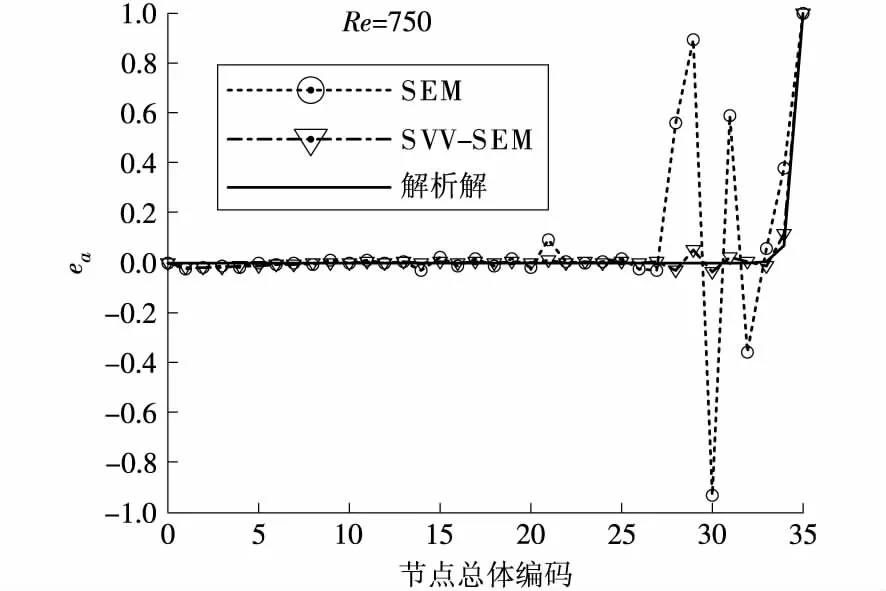
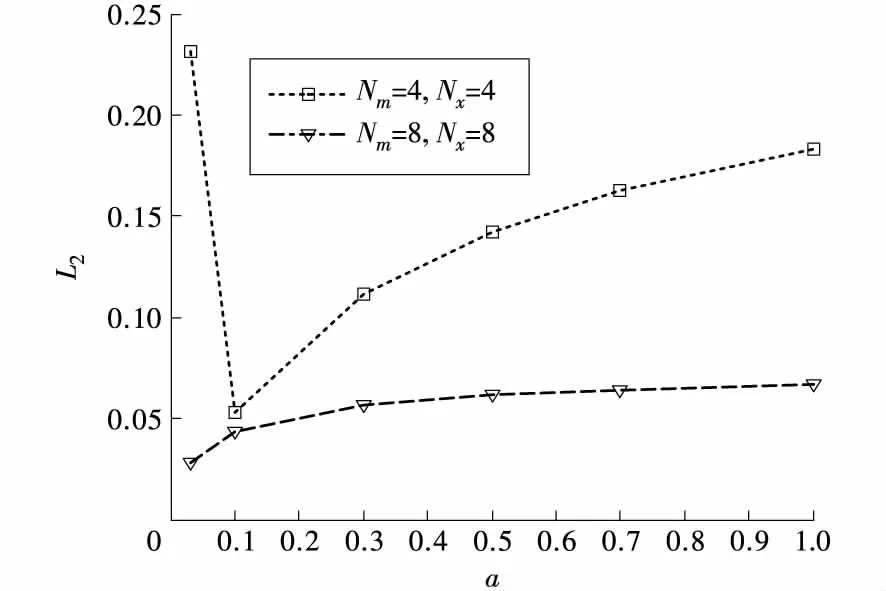
u(x,0)=u0(x),0 (2) u(0,t)=g1(t),u(1,t)=g2(t),t>0 (3) ε,Q依赖于用式(1)求解的多项式的阶数N,ε通常取ε≈N-1,Q在一维标准区域(-1,1)内的定义为: (4) 采用谱元方法求解式(1)~式(3)即为寻找u∈H1,使得在时间区间[0,1]上满足: ε(Qu,v)=(f,v),∀v∈H1, (5) 在边界上满足u(0,t)=g1(t),u(1,t)=g2(t),其中(·,·)表示定义在[0,1]上的L2内积。 由式(5)可得,谱消去粘性项的弱形式为: Svv(u,v)=ε(Qu,v) , (6) 为了保持其系数矩阵的对称性,可改写为: Svv(u,v)=ε(Q1/2u,Q1/2v) 。 (7) 由Chebyshev多项式的性质可知,式(6)、式(7)所表示的谱消去粘性项的弱形式并不完全相同,但式(7)保证了系数矩阵的对称性,可在计算中近似地采用。 实际计算时,将式(5)中的粘性项和谱消去粘性项相合并,则可以得到: (f,v),∀v∈H1, (8) 式中:S=I+εReQ,I为单位矩阵。 (9) (10) 在标准单元Λ内对式(8)进行离散,则可以得到第i个单元的谱元离散形式: (11) (12) 初始条件为:u(x,0)=u0(x)。 在时域上求解微分方程组一般有显式和隐式两种积分法。隐式积分法绝对稳定,但每一个时间步都需要求解线性方程组,显式积分法计算高效,需要的计算机内存小,但一般条件稳定。本文采用半隐式中心差分格式对时间项进行离散,对流项采用显式处理,粘性项采用隐式处理,融合了显式方法计算简单和隐式方法稳定性好的特点,式(12)的全离散形式为: c1un+1=c2un+c3un-1+Bfn, (13) 4.1谱消去粘性谱元方法稳定性条件 将式(13)两侧左乘c1的逆矩阵得: (14) 由于仅考虑第1类边界条件,即在边值的计算中不引入误差,所有的误差来自初始值的迭代过程。假定在初值的计算中引入了扰动τ0,则扰动τ满足: τn+1=M1τn+M2τn-1, (15) Dorsselaer等[11]分析了形如式(15)的全离散格式的稳定性条件,定义扰动Vn+1=((τn+1)T,(τn)T)T,其满足: Vn+1=EVn,n≥1 , (16) 可以验证当采用Chebyshev函数为单元基函数时,扰动系数矩阵E为正规矩阵。谱消去粘性谱元法求解稳定的充分条件为:矩阵E的谱半径ρ(E)≤1。 时永兴:谱消去粘性谱元方法求解对流扩散方程 4.2稳定性结果 图1 不同时间步长的稳定性曲线 将粘性振幅设置为ε=α/Nx,通过改变自由参数α的值,来研究ε的大小对求解稳定性的影响。图2给出了不同粘性振幅谱消去粘性谱元方法的求解稳定域。可以看出,对于较大的时间步长,ε值的增加对求解稳定域的扩大作用有限;对于较小的时间步长,求解稳定域随着ε值的增加不断扩大。说明对于较小的时间步长,较大的谱消去粘性项有利于求解稳定域的扩大。图2中截断阶数的设置为mN=Nx/2。 图2 不同粘性振幅的稳定性曲线 图3给出了不同截断阶数谱消去粘性谱元方法的求解稳定域。可以看出,对于2种时间步长,当截断阶数mN从Nx减小到2时,求解稳定域基本上保持不变;当截断阶数mN取0或1时,求解稳定域显著增加,同样说明较大的谱消去粘性项有利于求解稳定域的扩大。图3中粘性振幅的设置为ε=5.0/Nx。 图3 不同截断阶数的稳定性曲线 当f=0时,利用变量分离法可得式(1)的一个解析解为: (17) 相应的初始条件、边界条件: u(x,0)=0, 0≤x≤1 , (18) u(0,t)=0,u(1,t)=1 ,t>0 , (19) 该算例在边界x=1处有一个流动边界层的存在,当Re数增大时,边界层的厚度逐渐变小,速度变化剧烈,利用谱元方法进行计算时会产生数值振荡。 本文采用ea和L2误差来考察n时间层上数值解的准确性,两种误差的定义为: (20) (21) 通过数值解和解析解的比较来验证谱消去粘性谱元方法求解对流扩散方程的有效性。 5.1谱元方法和谱消去粘性谱元方法的精度比较 选取网格划分Nm=5,Nx=7,时间步长Δt=0.01,计算时间t=1.0,粘性参数ε=0.012/Nx,mN=Nx/2。由稳定性条件可以计算出对于所选定的时间步长和网格划分谱元方法求解的临界Re=557。谱元方法和谱消去粘性谱元方法在Re=570求解时,不同节点的绝对误差如图4所示。可以看出,在靠近边界层的区域谱元方法的数值结果已经开始发散,而谱消去粘性谱元方法的数值结果仍然和解析解相吻合。 图4 谱元方法和谱消去粘性谱元方法的绝对误差 谱元方法和谱消去粘性谱元方法在不同Re数的L2误差如图5所示。可以看出,谱元方法的L2误差随着Re数的增加逐步增大,特别是当Re大于临界值时数值结果快速发散;谱消去粘性谱元方法的L2误差随Re数的增加基本上保持不变,即使在稳定区域较小的谱消去粘性项的增加仍有利于计算精度的提高。 图5 谱元方法和谱消去粘性谱元方法的L2误差 5.2粘性参数对谱消去粘性谱元方法的影响 图6给出了谱消去粘性谱元方法不同ε值的L2误差。选取2种不同的网格划分Nm=4、Nx=4,Nm=8、Nx=8,研究粘性参数的变化对两种网格计算精度的影响。网格划分Nm=4,Nx=4的时间步长为Δt=0.05,相应的谱元求解临界Re=100,计算Re=150;网格划分Nm=8,Nx=8的时间步长为Δt=0.005,相应的谱元求解临界Re=874,计算Re=1 000。计算时间t=1.0,截断阶数mN=Nx/2。可以看出,在保证计算稳定的条件下,较小的粘性振幅有利于计算精度的提高,同时对于稀疏的网格,保证其计算稳定所需要的谱消去粘性项较大,即粘性振幅较大。 图6 谱消去粘性谱元方法不同ε的L2误差 图7给出了谱消去粘性谱元方法不同mN值的L2误差。选取网格划分Nm=4、Nx=6,Nm=6、Nx=6,研究截断阶数的变化对两种网格计算精度的影响。网格划分Nm=4、Nx=6的时间步长为Δt=0.02,相应的谱元求解临界Re=270,计算Re=350;网格划分Nm=6、Nx=6的时间步长为Δt=0.01,相应的谱元求解临界Re=500,计算Re=600。计算时间t=1.0,粘性振幅ε=0.1/Nx。可以看出,截断阶数的变化对于计算精度的影响不是十分明显,稀疏的网格需要较小的截断阶数以保证计算的稳定。对于Nm=4、Nx=6的网格其计算在mN=Nx-1时已经发散,而对于Nm=6、Nx=6的网格,其所需的谱消去粘性项较小,在mN=Nx-1时计算误差反而达到最小。 图7 谱消去粘性谱元方法不同mN的L2误差 本文采用Chebyshev谱元方法耦合谱消去粘性法求解了一维对流扩散方程,对该方法的求解稳定性和计算精度进行了分析,讨论了谱消去粘性参数对稳定性及计算精度的影响,并与谱元方法的求解结果进行了对比,可以得出如下结论。 (1)谱元方法在求解含有高Re数的对流扩散方程时稳定区域十分有限,谱粘消去粘性项的增加有效地扩大了稳定区域的范围。 (2)在高Re数时谱消去粘性项保证了谱元求解的数值精度,即使在稳定区域较小的谱消去粘性项的增加仍然有利于数值精度的提高。 (3)粘性参数的设置对于谱消去粘性谱元方法的稳定区域的扩大和计算精度的提高都有着非常大 时永兴:谱消去粘性谱元方法求解对流扩散方程 的影响。较大的谱消去粘性项有利于稳定域的扩大,但在保证计算稳定的条件下,较小的粘性项又有利于精度的提高。 今后的工作可以从以下两个方面展开:应用谱元方法求解非线性对流扩散方程,并对求解过程的稳定性和影响因素进行分析;将谱消去粘性谱元方法拓展至三维非定常流动。 [1]PETERA A T.A spectral element method for fluid dynamics:laminar flow in a channel expansion[J].J comp phys,1984,54(3):468-488. [2]陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2001:48-186. [3]MOHAMED S A,MOHSMED N A,ABDEL GAWAD A F,et al.A modified diffusion coefficient technique for the convection diffusion equation[J].Appl math comput,2013,219:9317-9330. [4]MOFID A,PEYRET R.Stability of the Chebyshev collocation approximation to the advection-diffusion equation[J].Comput fluids,1993,22(4-5):453-465. [5]TADMOR E.Convergence of spectral methods for nonlinear conservation laws[J].SIAM J numer anal,1989,26(1):30-44. [6]MADAY Y,OULD KABER S M,TADMOR E.Legendre pseudospectral viscosity method for nonlinear conservation laws[J].SIAM J numer anal,1993,30(2):321-342. [7]HEINRICHS W.Spectral viscosity for convection dominated flow[J].J sci comput,1994,9(2):137-148. [8]KARAMANOS G S,KARNIADAKIS G E.A spectral vanishing viscosity method for large-eddy simulation[J].J comput phys,2000,163:22-50. [9]XU C J,PASQUETTI R.Stabilized spectral element computations of high Reynolds number incompressible flows[J].J comput phys,2004,196:680-704. [10]KIRBY R M,SHERWIN S J.Stabilization of spectral/hp element methods through spectral vanishing viscosity:Application to fluid mechanics modeling[J].Comput methods appl mech.engrg,2006,195:3128-3144. [11]VAN DORSSELAER J L M,HUNDSDORFER W.Stability estimates based on numerical ranges with an application to a spectral method[J].BIT numer math,1994,34(2):228-238. (本文责编:白银雷) O 357.1 A 1674-1951(2017)10-0025-05 2017-08-07; 2017-09-13 时永兴(1972—),男,江苏常州人,工程师,从事火力发电厂生产管理工作(E-mail:syx_jrhd@126.com)。

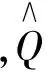

2 Chebyshev谱元离散
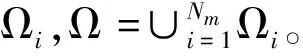


3 时间离散

4 稳定性分析


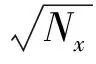



5 算例及分析


6 结论

